欧式空间在几何上的运用研究

郭 茜，吴桂康

（成都师范学院 数学学院，四川 成都 611130）

随着在实数域上线性空间中引入“内积”的概念，这样的线性空间就构成了欧几里德空间(Euclidean Space)，简称为欧氏空间，并随之得到向量的度量性质，如长度、两个向量的夹角等.通过向量的度量性质在解决几何问题上有着特殊的地位，比如勾股定理的证明[1]，平行四边形对角线的平方和等于各边平方之和[1]等等.

1 欧式空间中的有关结论

定义1[1]设V是实数域R上的一个线性空间，在V上定义了一个二元实函数，称为内积，记作α，β〉，它具有以下性质：

(1)（α，β）=（β，α）；

(2)（kα，β）=k（α，β）；

(3)（α+β，γ）=（α，γ）+（β，γ）+；

(4)（α，α）≥0，当且仅当α=0时（α，α）=0.

这里α，β，γ是V中任意的向量，k是任意实数，这样的线性空间V称为欧几里得空间.

定理1[1]令W是欧式空间V的一个有限维子空间，那么

因而V的每一向量ξ可以唯一地写成

这里 η∈W，＜ζ，W＞=0.

我们把子空间W⊥叫作W的正交补.η叫作向量ζ在子空间W上的正射影.

定理2[1]设W是欧氏空间V的一个有限维子空间，ξ是V的任意向量，η是ξ在W上的正射影.那么对于W中任意向量η'≠η，都有

定理2是几何空间中“垂线是最短距离”在n维欧氏空问中的推广,ζ在V的子空间W上的正射影η叫做W到ζ的最佳逼近（图1）.

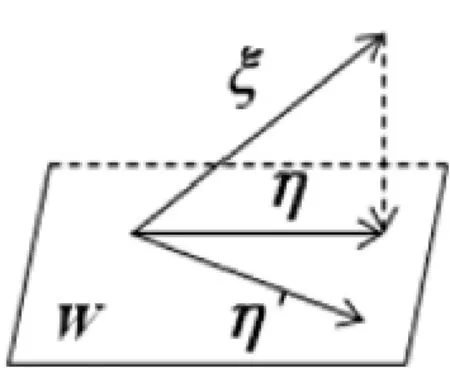
图1

定理3[2]在标准正交基下，向量的坐标可以通过内积简单地表示出来，即

α=〈ε1,α〉ε1+〈ε2,α〉ε2+…+〈εn,α〉εn.

2 主要结论

2.1 夹角和长度方面在几何上的应用

欧式空间中向量长度和夹角的定义正是解析几何中向量长度和夹角定义的自然推广.因此我们常常利用它们的相关性质，去解决几何上的相关问题.

例1[1]证明：一个三角形如果有一边是它的外接圆的直径，那么这个三角形一定是直角三角形.

证如图 2，设 |α1|=|α2|=|α3|，α1=-α3，ξ1=α3-α2，ξ2=α2-α1，利用“欧式空间中两个向量正交的充要条件是它们的内积为0”，于是

所以ξ1与ξ2正交，这个三角形是直角三角形.

图2

例2在实线性空间C[-1,1]中定义内积为：

求向量：α1(x)=1+x，α2(x)=-1，α3(x)=-x构成的三角形的三个内角.

解因为 α1(x)=1+x，α2(x)=-1，α3(x)=-x

则

又

2.2 正射影和距离在几何上的运用

最佳逼近有着许多重要的应用，比如解线性方程组、求直线型经验公式和求某些多元函数的极小值等等，下面我们来看一下它在几何方面的运用.

例3 设R3是三维欧氏空间，W是R3的子空间.且 ε1=(1，0，0)，ε2=(0，1，0)是 W 的一组基.若 α=(2，0，3)∈R3，试求α在W上的正射影是什么向量.

解设α在W上的正射影是β，则

例 4[3]证明：R3中向量（x0，y0，z0）到平面

证 在 R3中设 ζ=（a，b，c），η=（x0，y0，z0）.设 η'=（x'，y'，z'）是在上的正射影，则η-η'⊥W，且|η-η'|是η到W的最短距离.

因为对任意 ζ= （x，y，z）∈W，（ξ，ζ）=ax+by+cz=0，故ζ⊥W，于是向量η在W上的射曩为η'（图3）.设 ξ与的夹角为 θ，则

图3