基于改进粒子群算法的电力信息系统迁移方案

张迎平，眭建新，周沿东

（1.国网湖南省电力有限公司，长沙 410004；2.国网湖南信通公司，长沙 410004）

随着社会科技的不断进步与发展以及人民生活信息化水平的不断提高，个人和企业对于信息系统的依赖性越来越强[1-3]。信息系统是企业业务得以正常运转的基础，是关系到企业生存和发展的一种宝贵无形资产。而数据迁移是指在系统软件开发过程中，将其中具有实际价值的业务数据，依据功能需求或系统开发的要求，在不同的存储介质、存储形式或者计算机系统之间转移的过程[3-6]。虽然原有系统被新系统所取代，但是原系统积累的大量珍贵历史数据和用户信息等，都是新系统顺利启动所必须依赖的，这些历史数据也为企业后期进行数据分析和决策提供重要的参考依据。因此，对数据迁移的相关问题进行最优化求解具有重要的研究意义[7-9]。

1 信息系统迁移

在电力信息系统的建设过程中，由于电网企业用户业务规模和数量的不断扩大，系统软件的不断升级和硬件系统的不断更新换代（如硬件层次结构的增加、数据库版本的升级、运行环境的转换、多子系统的综合以及信息查询模式的多样化等），电网公司不可避免地需要面临信息系统相关数据的迁移问题。在迁移的过程中，如何保证用户业务的连续性，实现系统数据快速、平滑的迁移，把由于迁移带来的损失降至最低水平，是衡量迁移设计方案优越性一个重要标准。特别是，系统迁移得及时、准确将直接影响到新系统能否及时上线，也是影响新系统能否稳定运行的重要前提和根本保障。

目前，各个企业采用的数据迁移方案多种多样，如：文献[10]研究了基于勘探开发综合数据库PCEDM（petrol china engineer data model）的数据迁移方案，实现了将原始数据迁移到Oracle数据库PCEDM的技术方法，并在中石油勘探开发数据的实施取得了较好的应用效果；文献[11]对数据迁移过程中的数据库结构分析、数据迁移流程设计和数据迁移等实现步骤进行分析和研究，实现了政府办公室自动化新旧系统的正确、快速数据迁移；文献[12]对系统升级过程中数据迁移可采取不同方案进行适用情况和优点缺点比较，实现了新旧系统的顺利切换。然而，这些方案均局限于某个单一的应用领域，不具有普适性。

实际信息系统迁移中的诸多要素多种多样，要素之间的关联也较为复杂，如果对这些关联进行分析并实行调度优化，就可以找到一个系统性的方法来将迁移中所涉及到的要素间关联统一在一个模型框架下，进而实现信息迁移系统的最优化求解。在此，通过对国网湖南省电网公司信息系统迁移过程的相关要素进行抽象和分析，提取出影响系统迁移的多维特征描述向量，而后运用改进粒子群算法对系统迁移过程中的迁移时间开销问题进行优化设计，给出电力信息系统数据迁移时间开销最优化的解决方案，具有很好的普适性。

2 信息系统迁移模型的构建

国网湖南电力信息系统迁移项目，涉及面广，信息系统多，总共涉及ERP、财务管控、交易、用电信息采集、营销、IMS等17套核心应用系统；人资管控、财务核算、统计管理、基建管理、应急管理、安全监督管理和协同办公等53套重要信息系统；投资计划、信息安全档案管理、同业对标、统一漏洞补丁等42套一般系统。该项目具有以下的突出特点：

1）信息设备多。系统总共涉及各类信息设备约1162台搬迁，分别包括网络交换机、路由器、防火墙、负载均衡、机架PC服务器、刀片PC服务器、小型机、光纤交换机、FCOIP、磁盘阵列、磁带库等。

2）信息系统集成关系复杂。在运信息系统间涉及到的集成关系成千上万条，且使用的技术路线也不尽相同，比如通过ESB，数据交换平台，统一数据交 换 平 台 ，DBLink，Oracle Golden Gate，DSG，SAP RFC，SAP JCO，LDAP，JMS，等完成数据交换。

因此，该信息系统迁移中涉及各类要素不仅数量大，而且类型多，既包括硬件设备与系统，也包括软件系统与工具；既涉及硬件设备采购、运输、安装与调试，也设计软件系统的采购、开发、测试和部署；既需要满足时限要求，又需要兼顾经济成本，还需要估计可能的风险。为了在一个统一的模型框架下来研究和优化信息系统的迁移方案，需要对上述诸要素进行适当的抽象与描述，以满足普适性的模型的需求。

基于以上分析，文中提出了一种时间最优信息系统迁移模型TOISM（time optimal information system migration），即：

①机房集合 R＝｛r1，r2，…，rm｝，式中 rj为第 j个机房，j=1，2，…，m；

②信息系统集合 S=｛s1，s2，…，sn｝，式中 si为第i个信息系统，i=1，2，…，n；

③迁移系统序列集合 MS=｛ms1，ms2，…，msn｝，其中 msi=｛msi1，msi2，…，msik｝为系统 si中各设备的迁移顺序序列；

④可搬迁机房集合 MSR=｛msi1，msi2，…，msik｝，其中 msij=｛msij1，msij2，…，msijk｝为系统 si中各设备可迁移的机房；

⑤搬迁时间矩阵 T，tij∈T，式中 tij为第i个系统si搬迁至机房j所需要的时间；

⑦迁移目标 min f（Wt），即找出时间最短的迁移方案。

TOISM能够反映信息系统迁移过程中迁移方案的时间优化目标，求解模型的最优解，即确立最短迁移时间方案是一个典型的组合优化问题，为NP难问题，随着问题规模的增大，传统算法无法有效地进行求解。为此，针对TOISM文中提出了一种基于改进粒子群算法，用于TOISM的求解。

3 信息系统迁移方案优化

3.1 粒子群算法

受到鸟类群体运动模型的启发，Kennedy J.与Eherhart R.在1995年提出了粒子群算法PSO[13-15]（particle swarm optimization）。PSO 是一种基于群体的智能优化算法，群体中每一个个体（粒子）均为解空间中的一个潜在可行解，群体在解空间中进行全局寻优。每个粒子的位置为可行解，粒子通过速度来改变自身的位置，在求解过程中，每个粒子都保存自身经历过的最佳位置即个体最优解，群体也保存所有个体经历过的最佳位置即群体最优解。通过迭代过程，群体中所有粒子在解空间中进行全局搜索。从本质上而言，PSO是一种进化算法：

式中：vj，vj+1分别为粒子在第j次、第j+1次迭代时的速度；xj，xj+1分别为粒子在第j次、第j+1次迭代时的位置；c1，c2为学习因子， 通常为固定常数；r1，r2为随机数；pb，gb分别为粒子个体最优位置、群体最优位置；ω为惯性权重，按式（3）线性递减，即

式中：ωmax，ωmin分别为惯性权重的最大值、最小值；t为当前迭代代数；tmax为最大迭代次数。

3.2 求解TOISM的改进粒子群算法

粒子群算法具有全局寻优、收敛速度快等优点，因此得到了广泛的应用，但是标准粒子群算法的速度和位置更新非常适合于连续空间中的实数解空间，对于组合优化问题，则无法适用。虽然有基于离散空间的PSO改进算法，但多为通过将位置和速度转换二进制的方式来求解，而二进制PSO算法也不能直接应用于TOISM的优化。针对二进制PSO算法的特点，文中提出了一种改进PSO算法TOISM-PSO，用于TOISM的优化。

TOISM-PSO算法的基本流程与PSO算法一致，在具体环节的处理上则根据TOISM模型的特点进行改进。TOISM-PSO算法的基本思想是对PSO的位置和速度更新公式进行改进，以符合TOISM模型的特点。其基本处理流程如下：

步骤1生成初始群体

考虑到TOISM模型的数据为特定的机房与系统编号的组合，随机生成初始群体时通过限定器对个体进行限定，使生成的个体直接为有效解。限定器使用轮盘赌方式，随机生成初始化序列，并通过更新禁忌表进行限定。初始个体的结构如图1所示。

图1 ISMM-PSO个体结构Fig.1 Individual structure of ISMM-PSO

每个个体包含迁移序列与迁移机房信息。由图可见，系统迁移顺序为 so1→so2→so3→so4→…→son；对应的迁移机房分别为 ro1，ro2，ro3，ro4，…，ron。

步骤2评估个体适应度

此步骤TOISM-PSO与PSO一样，通过对个体进行适应度计算，评估群体中个体的适应度。适应度计算依据迁移时间开销进行计算。

步骤3更新个体最优和群体最优

此步骤TOISM-PSO与PSO相同，计算出个体的适应度后，与个体的历史最优及群体的历史最优进行比较，如果优于个体历史最优，则用当前个体替换个体历史最优，否则不更新；如果优于群体历史最优，则用当前个体替换群体历史最优，否则不更新。

步骤4更新个体位置与速度

TOISM-PSO的位置更新和速度更新采用与PSO类似的方式。速度更新采用式的方式，其中，当前位置与个体最优及群体最优的减法操作与PSO不同。针对TOISM模型的特点，减法操作分为2个部分，迁移序列之差与迁移机房之差，相应的结果作为影响当前速度的扰动因子。位置的更新采用式的方式，但生成的新位置需要使用限定器重新限定到有效解。

步骤5重新评估个体新位置的适应度

对个体的新位置进行适应度计算，并与原位置进行比较，如果新位置优于原位置，则替换原位置，否则不变。

步骤6输出最优解

判断是否满足结束条件。如果不满足，则转至步骤3进入下一轮迭代；如果满足结束条件，则输出群体最优解作为求解结果。

在信息系统多并发迁移模型中，涉及了诸如时间开销、成本开销、风险等多个决定优化目标的参数，这些参数往往因不同的迁移项目、不同的迁移要素以及不同的环境因素而存在变化。因此，需要研究此类优化参数的系统性的估计方法，从而使得整个优化建立在合理的基础之上。

3.3 模型求取最优解

信息系统多并发迁移项目中包含的迁移要素多，要素间的关联复杂，因此即使在完成了建模之后，也往往归结为一个大规模的优化问题。同时由于优化参数多，优化目标函数为非线性函数，因此存在着严重的局部最优问题，导致一般的优化方法难以获得性能较好的全局最优/次优解。因此需要针对这类问题研究其优化方法。

4 仿真试验及方案分析

4.1 数据预处理和参数设置

TOISM-PSO算法的参数设置见表1。其中的c1，c2分别对应粒子向个体最优、群体最优学习的力度。

表1 TOISM-PSO算法参数设置Tab.1 Parameter setting of TOISM-PSO algorithm

4.2 仿真试验

为了验证所提出的TOISM-PSO算法的有效性，进行了对比仿真试验。通过与基本遗传算法的对比，可以发现TOISM-PSO在收敛速度以及寻优结果方面都明显优于遗传算法，对比结果如图2所示。

4.3 迁移方案及分析

将TOISM-PSO算法应用到国家电网湖南省电力公司的信息系统迁移实际工作中，通过对各系统迁移的工作时间开销进行估计，统计出各信息系统迁移需要的时间开销，通过TOISM-PSO算法对信息系统迁移方案进行优化。其优化结果如图3所示。

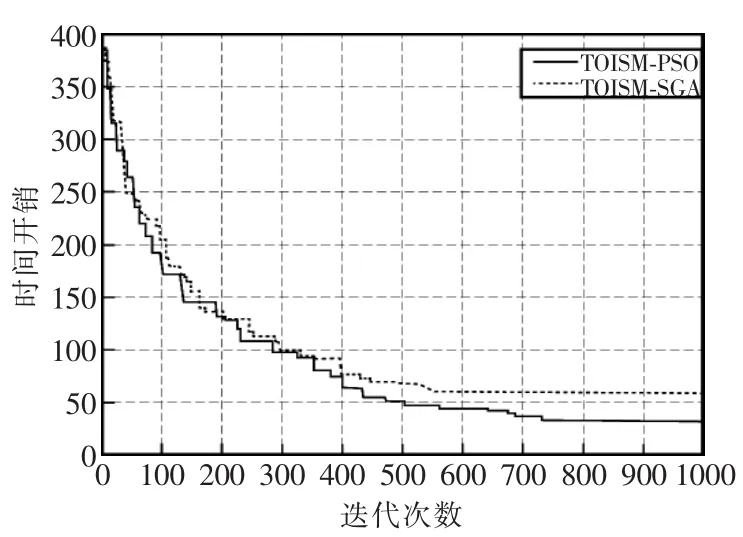
图2 算法的迭代寻优对比Fig.2 Iterative optimization comparison of different algorithms

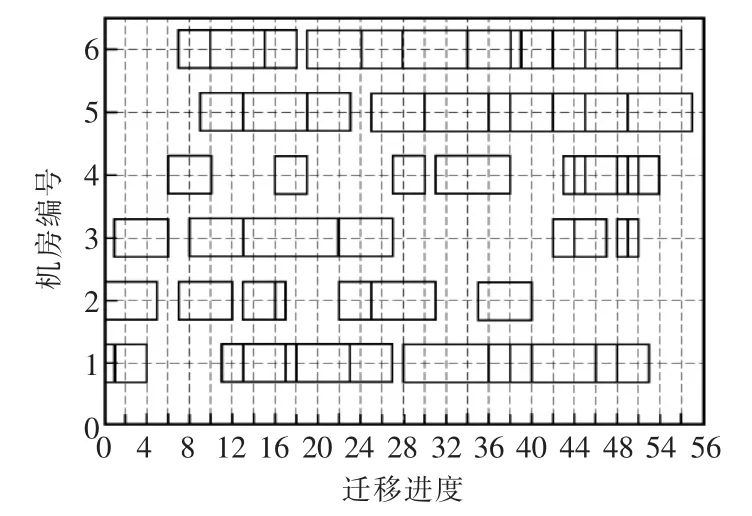
图3 信息系统迁移方案甘特图Fig.3 Gantt chart of information system migration scheme

5 结语

与传统的信息迁移系统相比，基于改进粒子群算法的电力信息系统迁移方案可以将信息系统迁移对日常业务的影响将至最低水平，能够实现整个系统迁移时间的最优化，可明显缩短信息系统更新与升级期间的系统停机时间，保持系统对外基本业务服务的连续性，减少系统更新与升级对客户体验造成的影响，最大限度地减少了企业的损失，具有很好的普适性和借鉴价值。