超声振动钻削的断续切削特性分析
毛 亮 ,邹 平 ,王 伟 ,陈 硕 ,3,田英健
(1.东北大学机械工程与自动化学院,辽宁沈阳110819;2.中航光电科技股份有限公司,河南洛阳471000;3.辽宁轨道交通职业学院机械工程系,辽宁沈阳110023)
超声振动钻削是在普通钻削的基础上,在钻头或工件上增加一个周期性的超声振动,使钻头和工件之间发生某种有规律的且可控的相对运动[1-2]。超声振动钻削过程中,通过选择合适的切削参数(振幅、频率、转速和进给量)可以改变钻削的加工机理,使其从普通钻削中的连续切削改变为断续切削(即刀具与工件周期性的分离与接触)。这种有规律的断续切削不但能抑制普通钻削加工中钻头的无规律振动,而且还能提高钻削系统的稳定性,从而提高孔的加工质量[3],特别是在加工难加工材料时能有效地减小切削力、提高入钻精度、排出切屑、降低切削温度、降低出口毛刺的高度和延长刀具寿命等,其优良的加工效果已经得到国内外学者的广泛关注[4]。
1 超声振动钻削轴向运动方程的建立
本文研究的超声振动钻削如图1所示,是在钻头的轴向上施加超声振动,使钻头既做进给运动也做轴向超声振动,使工件做旋转运动。选择工件旋转而不是钻头旋转,可避免在超声振动装置上安装集流环,使系统结构更加简单、安装操作更加方便。

图1 超声振动钻削示意图
由图1可见,规定水平方向为z方向,且向左的方向为正方向。当在钻头上所施加的超声振动为正弦波时,其波形函数为 z=Asin(2πft),则钻头的运动轨迹的表达式为:

式中:fr为钻头的进给速度,mm/r;n为工件的旋转速度,r/s;t为切削时间,s;A 为振动的振幅,mm;f为振动的频率,Hz。
2 超声振动钻削的断续切削特性分析
超声振动钻削的断续切削特性可从三个方面表现出来,具体是:一是切削时间的变化,由于超声振动具有周期性,当一个振动周期内只有部分时间在进行切削,而另一部分时间不进行切削,则可说明振动钻削的断续性;二是切削速度的变化,在普通钻削中钻尖相对工件的速度基本不变,而在振动钻削中钻尖相对工件的速度是变化的,当钻尖相对工件的速度是反方向时,则可说明振动钻削的断续性;三是切屑厚度的变化,普通钻削的切屑厚度不变,而超声振动钻削中,由于超声振动的施加,切屑厚度逐渐变化,当切屑厚度小于零(即钻头不再与工件接触)时,则可说明振动钻削的断续性。
2.1 超声振动钻削的切削时间分析
图2为超声振动钻削过程中刀具与工件的运动情况简图。可见,刀具一边做进给运动,一边做经过O点(O点位置随着进给运动不断变化)的往复振动。当进给速度满足一定条件时,在钻削过程中用于切削的时间就会减少,即出现了刀具与工件分离的情况。

图2 刀具与工件的运动情况简图
根据图2画出的刀具与工件接触及分离的时间简图见图3。刀具的振动周期为T、振幅为A;刀具从O点开始振动,且振动方向与刀具进给运动方向相同,此时刀具的振动速度最大。假设当刀具运动到ta时刻时,刀具与工件开始接触;ta时刻往后,刀具速度逐渐减小并减至0之后,其振动方向变成与刀具的进给方向相反,且刀具的振动速度逐渐增大;刀具经过切削时间tc之后,运动到tb时刻时,其振动速度大于刀具的进给速度,刀具就会和工件分离;tb时刻往后,刀具和工件分离,直到T+ta时刻再重新开始接触,该过程中刀具进给运动的位移和刀具振动运动的位移相同;T+ta时刻后,经过切削时间tc时,刀具和工件分离,再经过T+ta时刻后,刀具与工件又开始接触;刀具与工件之间不断的重复接触、切削和分离的过程,形成了振动切削过程中的断续切削[5]。
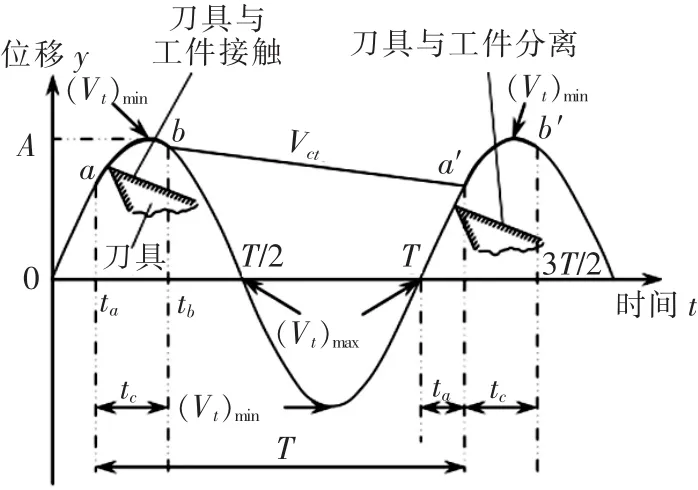
图3 刀具与工件的接触和分离时间简图
由式(1)可知,刀具相对于工件在Z方向的运动速度Vz的表达式为:

若要使刀具和工件在切削过程中分离,需刀具与工件在钻削方向上有相对速度Vz>0的时刻。因为只有当Vz>0时,钻头才会相对于工件做向左的运动(图1),即钻头不再切削工件,从而可得断续切削的条件为:

由图3可见,当t=tb时,刀具和工件分离,此时刀具与工件在钻削方向上的相对速度为0,即:

另外,由于在刀具和工件从b处开始分离到从a′处开始接触的过程中,刀具和工件的位移一样,因此可得:

在此,定义刀具和工件的净切削时间比r为:

由式(7)可知,刀具和工件的净切削时间比r与进给量fr、转速n、振动振幅A和振动频率f有一定关系。当给出其中三个参数的值,只改变另外一个参数的值时,利用Matlab编程绘出净切削时间比r随着某个参数变化的趋势见图4。
由式(4)、式(5)和式(6)可得[6]:


图4 净切削时间比r随着振幅A、频率f、进给量fr和转速n变化的趋势图
由图4可知,净切削时间比r随着振动振幅A和振动频率f的增大而减小,且减小的速率逐渐减小;净切削时间比r随进给量fr和转速n的增大而增大,当进给量fr和转速n达到一定值后,净切削时间比r值恒为1,此时就不能实现断续切削。
由前面的分析可知,要想实现断续切削需满足刀具与工件在钻削方向上的相对速出现大于0的情况,即满足式(3)所示的断续切削的条件。假设转速 n=45 r/s、振动频率 f=2000 Hz、振幅 A=0.02 mm,并将其值代入式(3),则得到的实现断续切削所需进给量fr的取值范围为:
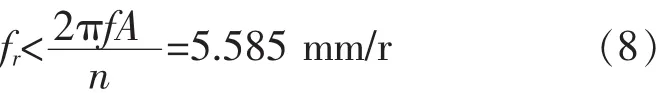
由图4c可见,当进给量fr>5.585 mm/r时,净切削时间比r始终等于1;当进给量fr<5.585 mm/r时,净切削时间比r始终小于1,此时表现出断续切削的特性。同理在图4a、图4b、图4d中也可验证式(3)的断续切削条件。只有满足式(3)的断续切削条件,才能实现断续切削。
2.2 超声振动钻削的切削速度分析
超声振动钻削过程中钻头相对工件的实际运动速度是由钻头的轴向运动速度Vz和工件的旋转运动速度Vr共同组成的。工件上到钻孔圆心距离为r某点的旋转速度Vr的表达式为:

从而可得钻头相对工件的实际运动速度V的表达式为:

根据式(10)可画出钻头相对工件的实际运动速度V随时间t和距离r的变化趋势图(图5)。

图5 V随时间t和距离r的变化趋势图(×10-4)
为了进一步了解钻头相对工件的实际运动速度变化情况,绘出了ΔV=Vmax-Vmin随着距离r的变化曲线图(图6)。其中,Vmax代表钻头刀刃上某一点处的最大切削速度,Vmin代表钻头刀刃上某一点处的最小切削速度。由式(10)可以得出Vmax和Vmin的表达式分别为:

从而可得ΔV的表达式为:
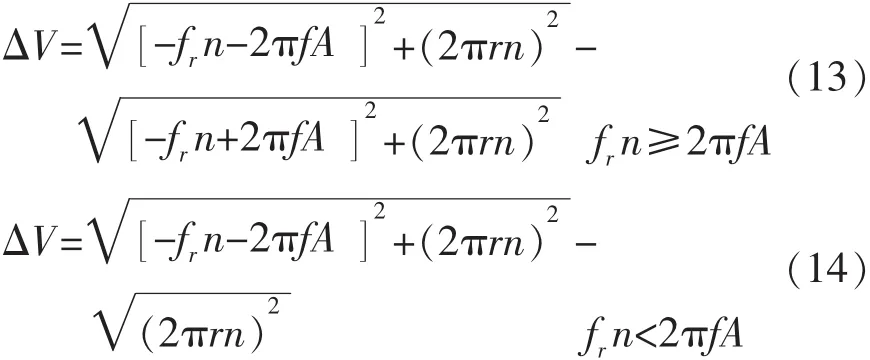
由图6a可见,当frn≥2πfA时,ΔV的值很小,钻头相对工件的实际运动速度V的变化很小;由图6b可见,当frn<2πfA时,ΔV的值很大,即钻头相对工件的实际运动速度V的变化很大。由此间接证明了式(3)所示的振动钻削断续切削条件的正确性,即振动钻削可以实现钻削的断续性。
2.3 超声振动钻削的切屑厚度分析
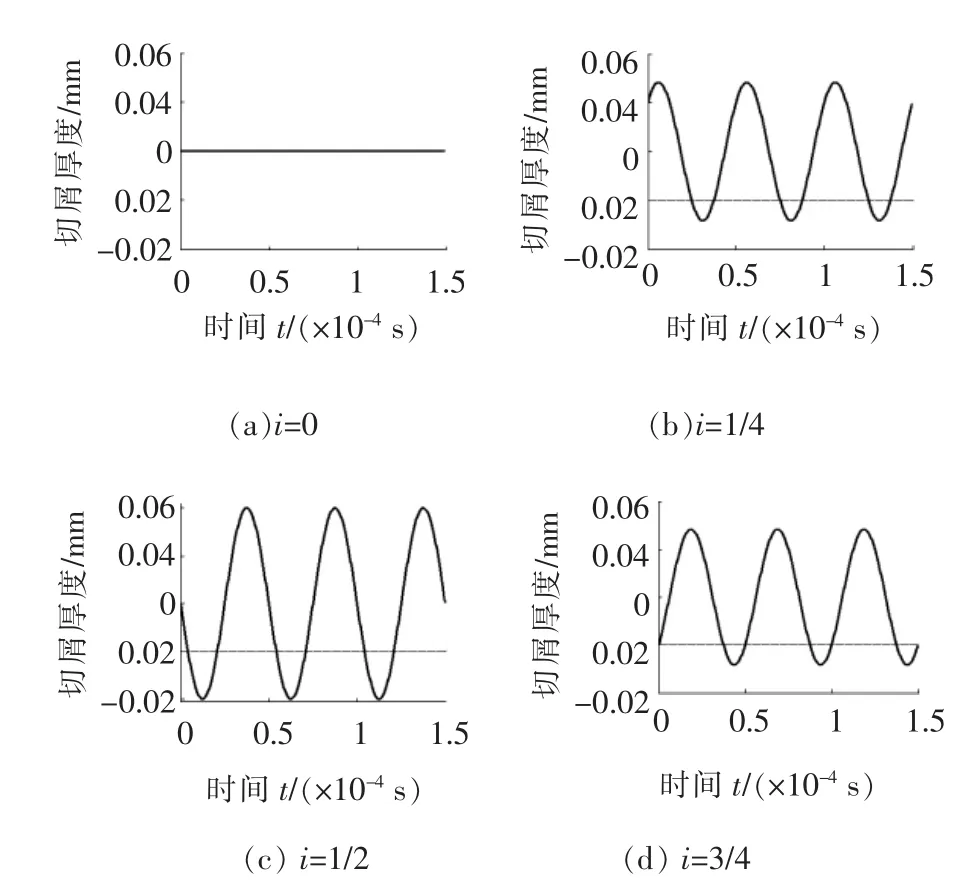
在刀具相对工件运动过程中,定义工件转半周的时间内刀具振动次数为重叠次数M,则表示为:

图6 不同条件时ΔV随着距离r的变化曲线图

式中:K代表整数部分;i代表小数部分,且0 由工件的转速n可得出工件转半周所用的时间为1/2n秒。再由式(1)和式(15)可得出工件在第0、1/2、1、3/2……m/2转时, 钻头的两条切削刃沿轴向的位移分别为: 由式(16)可得相邻两切削刃之间的切屑厚度的表达式为: 式中:m=0,1,2,3……。 由式(17)可知,相邻两切削刃之间的切屑厚度与进给量fr、振幅以及振动频率与工件转速的比f/2n(即i)有关,且该切屑厚度以fr/2为中心、以2Asin(πi)为振幅、以f为频率发生周期性的变化。 不同i值情况下的切屑厚度见图7。可知,当i取适当的值时,切屑厚度会出现小于零的情况,即钻头与工件分离,从而实现断续切削。 因为 0 图7 不同i值情况下的切屑厚度 在不考虑切屑收缩系数的情况下,要想实现断续切削,则只需满足smmin<0,从而得出实现断续切削的一个条件为: 把式(15)代入式(17)得: 式中:K为式(15)中重叠次数的整数部分。 若要实现断续切削,则进给量fr、振动振幅A、振动频率f和转速n之间的关系应满足式(20)。根据式(20)绘出的理论断续切削区域图见图8。 图8 理论断续切削区域图 从分析超声振动钻削的切削时间、切削速度和切屑厚度的过程中可见,超声振动钻削具有断续切削特性,但并不是所有的超声振动钻削都能实现断续切削,只有当进给量fr、转速n、振幅A和振动频率 f满足 frn<2πfA 和的关系时,超声振动钻削才能实现断续切削。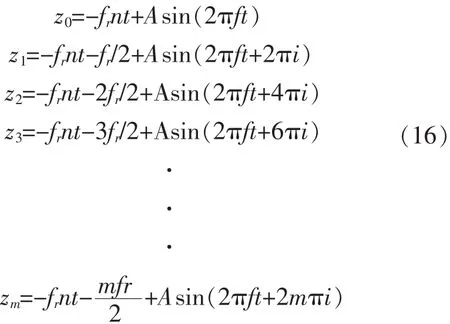





3 结束语

