粒子群优化-协同克里金法在确定山地斜坡土层厚度中的应用
王桂林,向林川,孙帆
(重庆大学 a.山地城镇建设与新技术教育部重点实验室;b.土木工程学院, 重庆 400045)
随着中国城镇化进程的不断推进,为了更有效地保护优质耕地,国土资源部提出了开展低丘缓坡等未利用土地开发试点的工作。残坡积土是低丘缓坡重要的组成部分,高质量的残坡积土层厚度信息在土地资源管理、工程建设、地质灾害预警预报等方面具都有重要意义。获取比较精确的土层厚度数据的方法之一是布设高密度的钻孔,但由于受到经济水平、技术手段和地形条件的限制,钻孔点的数量是一定的,这为确定土层厚度带来了较大的误差。随着地统计学理论在工程界不断应用,空间插值的方法也日益成为解决上述问题的经典方法。将利用统计学与地理信息系统相结合的方法,基于已知钻孔点的观测数据进行空间插值来获得估计点的土层厚度。
空间插值是利用已知的部分空间样本信息,对未知地理空间的特征属性值进行估计,是地理信息系统的重要功能模块之一[1],并在矿业、水文、气候预报、农业等领域有着广泛的应用。目前已发展了较多的空间插值方法:如泰森多边形法[2]、克里金(Kriging)插值法[3]、反距离加权平均法[4]、趋势面分析法[5]、多项式回归法[6]等。但这些方法只是局限于已知点的单一属性值,没有考虑到其他因素对待估计点属性值的影响(如高程对土层厚度的影响等)。
基于上述方法在估计空间属性值时对变量考虑的单一性,学者提出了一种能考虑多个相关变量互相影响的协同克里金法。Yates等[7]将裸土表面温度和土壤沙粒含量作为协变量,利用协同克里金法(Co-Kriging)估计质量含水率;Ghadermazi 等[8]利用pH值作为辅助变量,估计了饮用水中硝酸盐的含量。胡丹桂等[9]用考虑降雨量的协克里金法来研究空气的湿度的空间变化;许晶玉等[10]用考虑土壤粗砂含量和全氮含量的协克里金法来研究山东省种植区地下水硝态氮污染空间变异及分布规律;杜文凤等[11]将地震数据引入协克里金法中估计煤层厚度的分布规律;黄大年等[12]首次将重力梯度引入协克里金法中来研究岩脉倾向的问题。
半变异函数是克里金法中反映区域化变量空间变化特征的有效数学模型,由其确定拟合模型参数直接影响插值精度。严华雯等[13]通过利用加权最小二乘法优化遗传算法中的适度函数,改进普通基于遗传算法优化的克里金插值方法;张强等[14]采用基于线性递减权值的粒子群算法估计半变异函数参数的方法,提高了插值的精度;贾雨等[15]将约束粒子群优化算法用于克里金的插值研究,结果表明能获得较好的插值精度。
本文采用粒子群优化算法与协同克里金法相结合的方法对土层厚度的空间插值进行研究,并对插值结果进行对比,以期提高土层厚度插值分布的精度。
1 方法原理
1.1 普通克里金插值法
克里金插值法又称空间自协方差最佳插值法,是以南非矿业工程师D.G.Krige的名字命名的一种最优内插法。该方法首先考虑的是空间属性在空间位置上的变异分布,确定对一个待插点值有影响的距离范围,然后用此范围内的采样点来估计待插点的属性值。该方法考虑了已知信息与待估计点相互间的空间结构特性。为达到线性、无偏和最小估计方差的估计,而对每一个样品赋予一定的权重,最后进行加权平均来估计待预测点属性值的一种方法。
在克里金法中,用来衡量各个样本点之间空间相关程度的是半变异函数
(1)
式中:h为两点之间距离;N是由h分开的成对样本点的数量;Z是点的属性值。
一种典型的半变异函数图像如图1所示,半变异值随距离增大而增大,其中有两个非常重要的点:间距为0时的点以及函数趋于平稳时的拐点,前者表示的是两个非常接近的样本点之间的误差及空间变异,后者表示两样本点超过此间离后将不存在空间相关性。
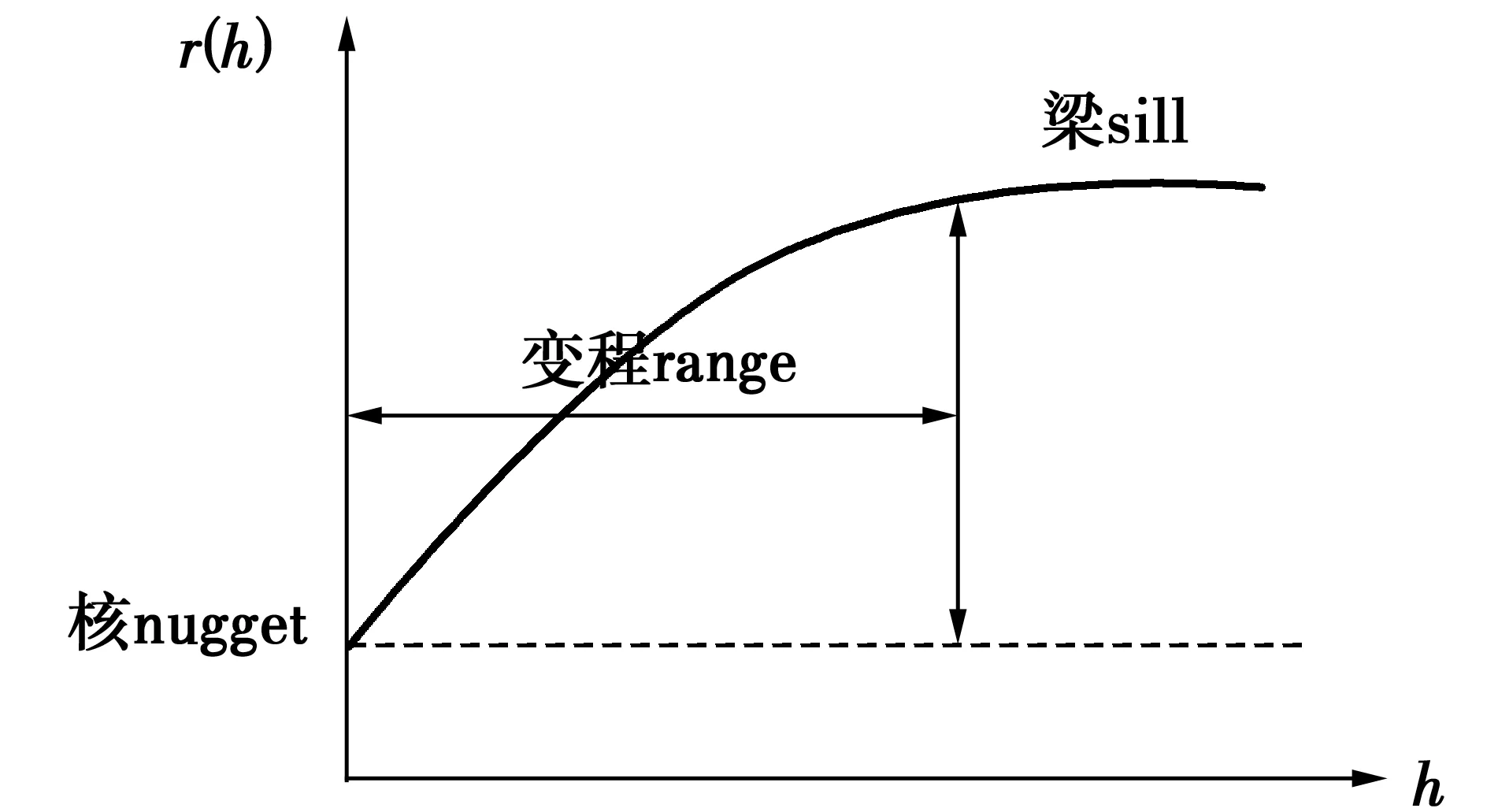
图1 半变异函数图
通过式(1)确定半变异函数云图,然后再拟合出相应的模型表达式,应用式(2)确定内插所需要的权重,并通过式(3)进行未知样本点属性值的估计。
(2)
(3)
式中:λi为待定的权重;u为拉格朗日乘子;r(hij)为xi与xj两点的半变异函数;N为样本点数量;x0为待插值点,Z为其属性值。
1.2 协同克里金法
协同克里金插值法可以利用同一变量在不同时空或不同变量在同一时空上的协同区域化性质,用易于测定的变量来对那些难以测定的属性或变量进行估值,或者用样品多的变量对样品少的变量进行估值;如果两种以及多种属性具有显著的空间相关性,则可以优先考虑协同克里金插值法。
在协同克里金法中,γ11、γ22分别表示变量1与变量2的半变异模型函数,其计算方法与普通克里金插值法中的半方差计算方法相同;γ12为协半变异函数,是用来衡量两个变量各个样本点之间空间相关程度的表达式
[Z2(xi)-Z2(xi+h)]
(4)
式中:h为两点之间距离;N是由h分开的成对样本点的数量;Z1是点关于变量1属性值;Z2是点关于变量2属性值。
拟合后用式(5)即可确定空间插值所需要的权重,并通过式(6)进行未知样本点属性值的估计。
(5)
(6)

1.3 粒子群优化算法
粒子群优化算法(PSO)是一种进化演变技术,最早是由美国的心理学研究者 Kennedy博士和从事计算智能研究的Eberhart博士受到人工生命的研究结果启发于 1995 年提出的一种基于群智能的优化算法[16-17]。
粒子群算法的实质是一种信息共享,粒子根据自身的个体最优信息及群体的最优信息不断更新自己的速度和位置,最后收敛于全局最优解。每个粒子都有一个有待优化问题所决定的适应度值用来评价该粒子的优良程度,一个粒子还有一个速度用于决定它的运动距离即速度,粒子根据自身的运动经验和群体中其它粒子的运动经验来调整自己的运动。粒子从此时刻运动到下一时刻的速度由式(7)确定,位置由式(8)计算得到。具体流程见图2。
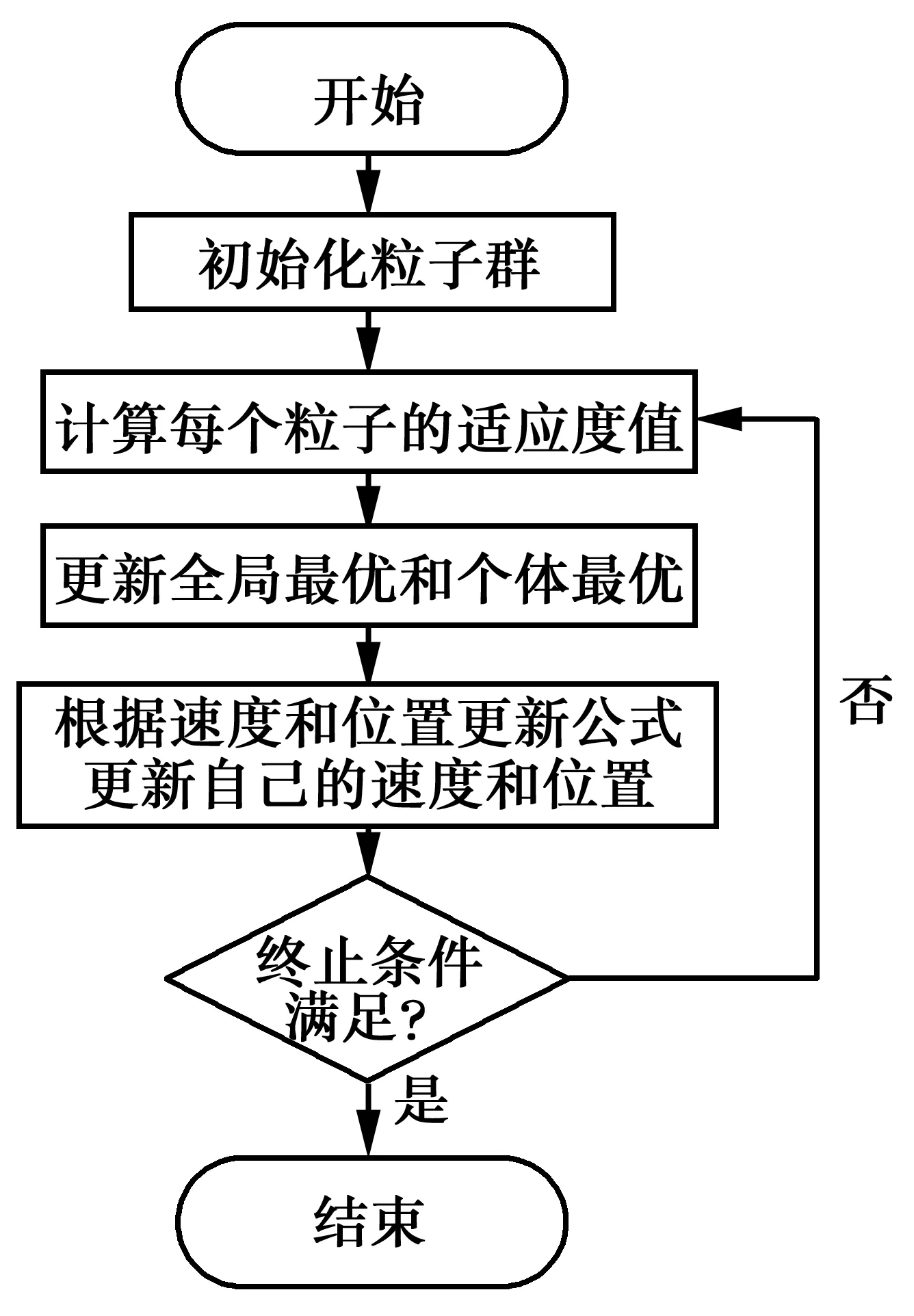
图2 粒子群优化算法流程图Fig.2 The flow chart of particle swarm
(7)
xij(t+1)=xij(t)+vij(t+1)
(8)
式中:i为第i个粒子,j为第j个维度;t为更新次数;v为粒子速度,x为粒子位置;r1、r2为0到1均匀分布的随机数;xpbest粒子自身最好位置,xgbest全局最好位置;ω为惯性权重值。
1.4 基于粒子群优化算法的克里金插值法
拟合半变异函数的模型有很多种,但无论是哪种拟合模型,都涉及到3个拟合参数,分别是图1中的核(nugget)、变程(range)和梁(sill)。在通常情况下,无论是普通克里金法还是协同克里金法,在确定上述3个参数时用的均为最小二乘法,即在满足方差最小的条件下得到的,这就会使得3个参数存在较大的误差。利用粒子群优化算法能快速寻找到全局最优解的特点,将该优化算法应用到确定半变异模型3个参数上。其中该优化算法中的适应度函数为插值结果的均方根误差。
同时,大量研究表明, PSO算法易陷入局部最优和早熟收敛等缺陷。采用一种基于高斯变异的方法来提高种群的多样性[15]。在算法出现过早收敛时,能够使粒子在其他区域进行搜索,跳出局部最优,寻找更优的解。即在迭代到一半次数后,开始对粒子进行变异,对每个粒子进行高斯变异[18]。公式为
xd=gbest(d)×(0.5+σ)
(9)
式中:gbest(d)为全局最优在d维的值;σ为高斯白噪声。
1.5 预测精度评价方法
为了能够对上述方法的空间插值精度进行比较,使各方法间的结果更具有可比性,可通过计算钻孔点的勘察数据与预测数据的误差来评估各种方法的优劣[19]。均方根误差(RMSE)可以用来评价预测值和真实值之间的接近程度。利用协同克里金法与普通克里金的均方根误差减少的百分数(RRMSE)来表示预测精度的提高程度。
(10)
(11)
式中:Z(xi)与Z*(xi)分别为xi处的勘察值与估计值;N为样本数量。
2 工程实例
2.1 研究区域概况与数据处理
2.1.1 研究区域概况 试验区位于重庆万盛经济开发区,地貌单元为丘陵斜坡地貌;总体趋势为西侧高,东侧低;地表总体坡度2°~34°。上图中的红色部分为钻孔点的位置,已知数据有勘察区的平面图、剖面图及钻孔柱状图。试验区最高海拔为418.23 m,最低海拔为334.77 m;共有124个钻孔点。具体情况见图3。
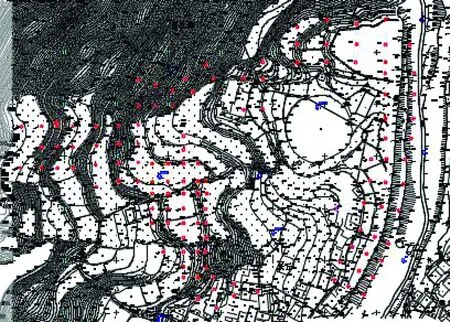
图3 试验区钻孔分布图Fig.3 The distribution of
2.1.2 钻孔点数据处理与分析 对试验区124个钻孔的高程数据和土层厚度分析,结果显示:土层厚度和钻孔点的高程有一定的规律(为了便于与土层厚度比较,高程基准点设为320 m),具体表现为:在一定的高程范围内,钻孔的土层厚度大致和高程值成正相关(见图4)。
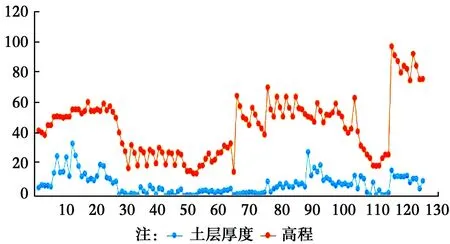
图4 土层厚度和高程关系图Fig.4 The correlation between soil thickness and
协同克里金法中,作为辅助变量的前提条件是该变量与待估计变量之间存在着相关性。用SPSS统计软件中的数据分析功能得到高程值和土层厚度的相关系数为0.552,且在0.01的显著性水平的条件下,相关性程度为显著性相关(表1)。因此,可将高程值作为提高土层厚度插值精度的辅助变量。
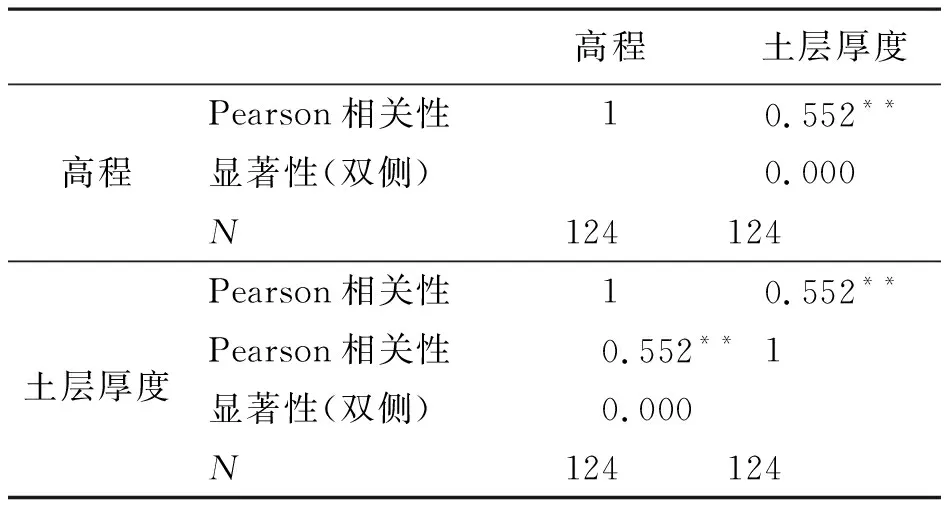
表1 SPSS统计软件计算结果Table 1 The result calculated by SPSS statistical software
注:**水平(双侧)上显著相关。
2.2 空间插值模型试验
采用交叉验证的方法[20]来估计土层厚度,并用数理统计的方法来比较不同估计模型的估值精度,即首先将待预测点的属性值Z(xi)暂时剔除,然后将最小二乘法得到的半变异函数表达式用于普通克里金法和考虑高程的协同克里金法来预测Z(xi)的值。结合相应的公式并利用MATLAB编制程序求出拉克朗日系数和待估计点的影响范围内的各个钻孔点的权重系数,最后利用式(3)与式(6)分别求出待估计点的属性值Z*(xi)。重复以上过程直到对所有的124个观测点进行估计。
基于粒子群优化算法的克里金插值法与基于最小二乘法的克里金插值法区别在于:粒子群优化算法中的半变异模型中的3个参数是未知的;随机的给每个粒子赋值,这样每一个粒子就对应了一个半变异函数的模型;然后将每个粒子所对应的半变异函数模型,带入用MATLAB编制的相应插值程序中,求出均方根误差,并且将该均方根误差作为该粒子的适应度函数的适应值。当循环结束后,最小的适应度值的粒子即为所求。进而求出了半变异函数的表达式。
无论是哪一种方法,每一个钻孔点可以得到真实值和估计值两类数据。将各个插值方法得到的插值结果与真实值做成火柴棍图,见图5~图8。
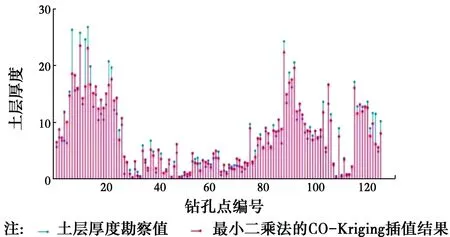
图5 最小二乘法的O-Kriging插值结果与真实土层厚度Fig.5 O-Kriging based on the least squares method interpolation results and the true soil
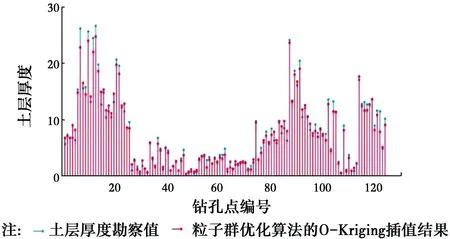
图6 粒子群优化算法的O-Kriging插值结果与真实土层厚度Fig.6 O-Kriging based on PSO method interpolation results and the true soil
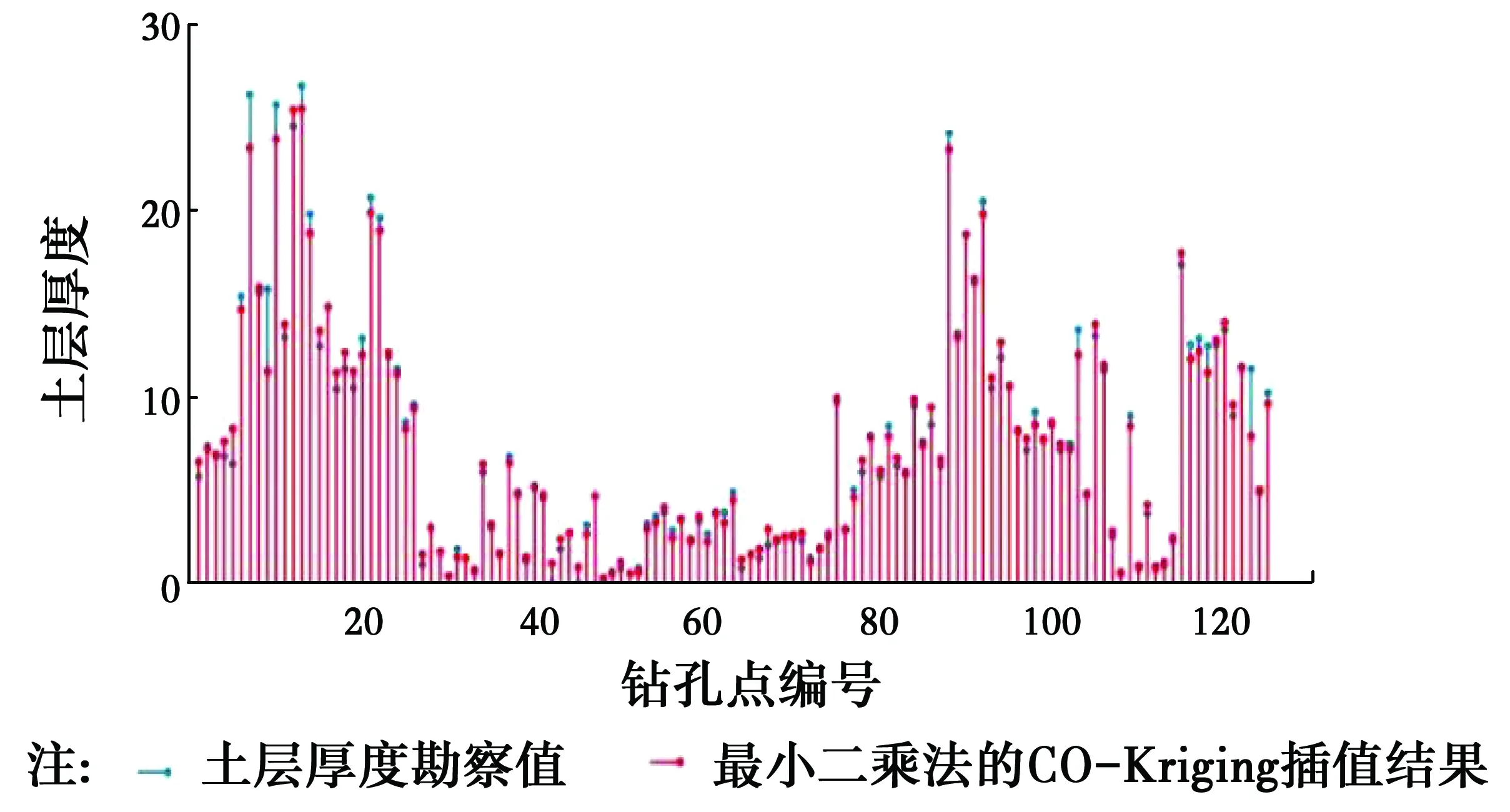
图7 最小二乘法的CO-Kriging插值结果与真实土层厚度Fig.7 CO-Kriging based on the least squares method interpolation results and the true soil
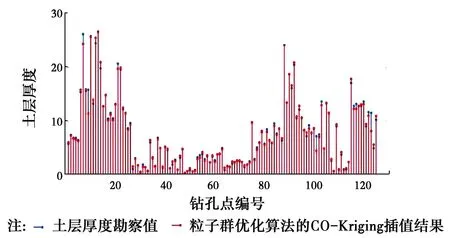
图8 粒子群优化算法的Co-Kriging插值结果与真实土层厚度Fig.8 Co-Kriging based on PSO method interpolation results and the true soil
从图5~图8中可以看出,在上述的4类方法中,基于最小二乘法的普通克里金插值法与勘察值之间的误差是最大的;而考虑高程的协同克里金法的插值的精度要高于基于粒子群优化算法的普通克里金法;基于粒子群优化算法的协同克里金插值法的精度在4类方法中是最高的,除了极个别的土层厚度较厚的钻孔点外,其他钻孔点均与实际情况吻合得较好。
用数理统计的方法来比较4种插值结果的精度的提高程度。其结果见表2。
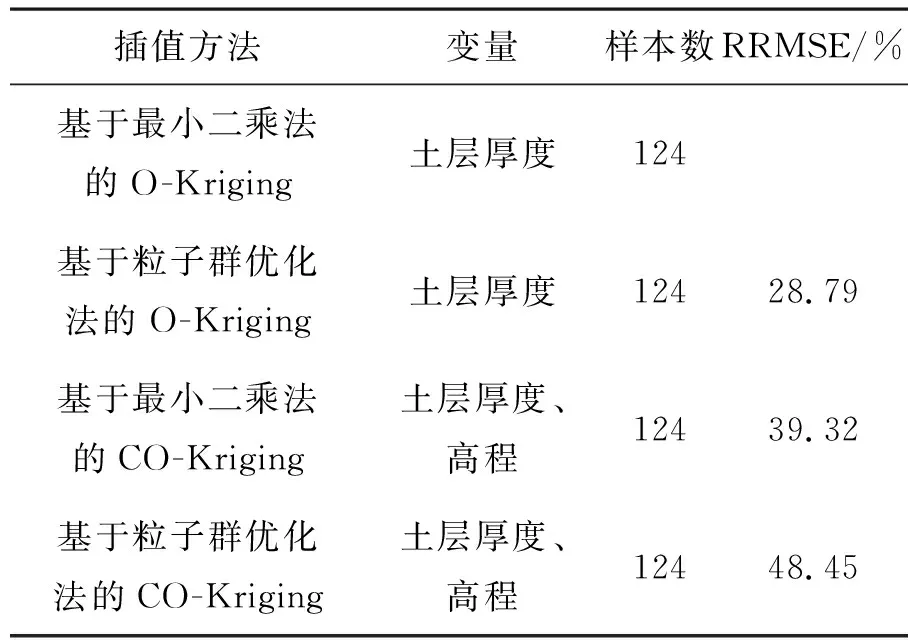
表2 O-Kriging与Co-Kriging预测精度的比较Table 2 Error analysis of O-Kriging and Co-Kriging
从表2可以看出,当采用普通克里金插值法对边坡的土层厚度进行空间插值时,基于粒子群优化算法的普通克里金插值法较基于最小二乘法的普通克里金插值法的均方根误差减少了28.79%;当均采用最小二乘法去拟合半变异函数时;协同克里金法的均方根误差较普通克里金法减少了39.32%;当都采用PSO法去拟合模型参数时;协同克里金法的均方根误差较普通克里金法减少了19.66%;同时还可以从表中得出结论:当考率单一因素时,考虑高程的协同克里金法较基于粒子群优化算法的普通克里金插值法的插值精度提高了10.53%。
3 结论
以重庆某坡地为研究对象,利用该区域勘察报告中的124个钻孔点的勘察数据为试验样本,采用交叉验证的方法分别用普通克里金插值法和考虑高程的协同克里金插值法对土层厚度进行虚拟差值。还对在拟合半变异函数模型参数时存在的误差进行了研究,用粒子群优化算法拟合半变异函数模型,并对4种不同方法的插值结果进行了对比分析,得到的结论如下:
1)将最小二乘法拟合的半变异函数用于普通克里金法插值时会产生较大误差。
2)对土层厚度进行克里金插值时,考虑高程的协同克里金法较普通的克里金法的插值精度高。
3)通过交叉验证表明,粒子群优化算法能在一定程度上提高普通克里金插值法和协同克里金插值法的插值精度。

