基于四阶段法的大型车超速辨识模型及其优化

包 旭，陈锦文，张山华，殷永文

（1.淮阴工学院 江苏省交通运输与安全保障重点建设实验室，江苏 淮安 223003；2.南京工业大学 交通学院，江苏 南京 210009；3.淮安市交通运输局，江苏 淮安 223001）

0 引 言

凭借运量大、速度快等优势，大型车已成为国内道路客货运的主要载运工具之一，与之而来的是大型车垂直侧碰电动自行车的事故频发。在事故鉴定中对大型车进行超速辨识显得愈发重要。

文献[1-2]利用多普勒效应及雷达实现机动车的超速检测，然而此方法受限于仪器安装位置，无法应用于道路交通全路段；文献[3-5]利用安装在车内和道路上的传感器或传感器网络感知机动车速度，然而此方法成本较高，对传感器的稳定性要求严格；文献[6-9]通过视觉感知原理、迭代算法以及视频监控、图像处理技术进行目标追踪，实现了车辆超速监测，然而此方法对能见度要求较高，受气象条件影响较大。

文献[10]定义了垂直侧碰，通过骑车人抛距与碰撞速度的经验公式和动能定理，逆向还原车辆制动时刻速度，提出垂直侧碰电动自行车的小汽车超速辨识模型，可以快速确定小汽车制动时刻速度。然而该模型并未考虑汽车碰撞点高度的不同，产生的骑车人抛出轨迹以及抛距的差异，导致其应用于大型车超速辨识时精度不高。基于此，本文设计一种基于四阶段法的大型车超速辨识模型（OILV），并在此基础上，构建基于BP神经网络的优化模型（BP-OILV），可精确稳定地辨识事故中大型车是否超速。

1 基于四阶段法的大型车超速辨识模型

本文关于垂直侧碰、制动时刻速度和抛距的定义与文献[10]相同。

定义1：大型车碰撞速度v为大型车与电动自行车、骑车人接触，且电动自行车、骑车人原运动状态尚未改变时大型车的速度。

定义2：大型车碰撞后速度v′为大型车与电动自行车、骑车人接触，且电动自行车、骑车人原运动状态开始改变时，大型车的速度。

大型车垂直侧碰电动自行车事故的发生过程如下：碰撞前大型车在t1时刻以速度v0紧急制动，并在t2时刻以速度v与电动自行车和骑车人发生碰撞；碰撞后大型车以v′继续制动，并在t3时刻静止，骑车人和电动自行车碰撞后分别以抛出速度v1和v2做平抛运动，并在t4时刻和t5时刻落地（t3，t4，t5时刻先后顺序由具体碰撞事故决定，不影响本文事故分析）；骑车人和电动自行车在大型车行驶方向上作平抛运动、滚动和滑动后并分别在t6时刻和t7时刻静止（先后顺序不影响本文事故分析）。因此本文以碰撞时刻t2为间隔点，逆向分析事故，将大型车垂直侧碰电动自行车事故分为四个阶段。其中，阶段一为计算骑车人和电动自行车的抛出速度；阶段二为计算大型车碰撞后速度；阶段三为计算大型车碰撞速度；阶段四为计算大型车制动时刻速度。基于四阶段法的大型车超速辨识如图1所示。

图1 基于四阶段法的大型车超速辨识示意图Fig.1 Schematic diagram of large vehicle overspeed identification based on four-stage method

阶段一：计算骑车人、电动自行车的抛出速度。

碰撞后，骑车人抛出，其受方向相反的两个力mg和N(t)，N(t)为骑车人受到的竖直向上的反力，且随时间变化。

设ax，ay为加速度分量（单位：m/s2），φ为路面附着系数，m1为骑车人质量（单位：kg），H1为骑车人重心高度（单位：m），v1为骑车人抛出速度（单位：m/s），s1为骑车人抛距（单位：m）。

根据牛顿第二定律，可得：

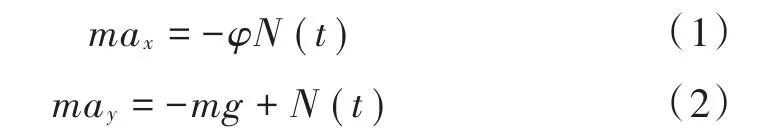
联立式（1），式（2）得：

对式（3）两边进行积分可得速度分量关系式：

对式（4）两边进行积分可得位移分量关系式：

当t=0时，x=0，y=H1，vx=v1，vy=0，代入式（4），式（5）可得：

此时，速度分量关系式（4）为：

位移分量关系式（5）为：

当骑车人最终静止时，vx=0，vy=0，x=s1，y=0，t=ttotal，代入式（8），式（9）可得：

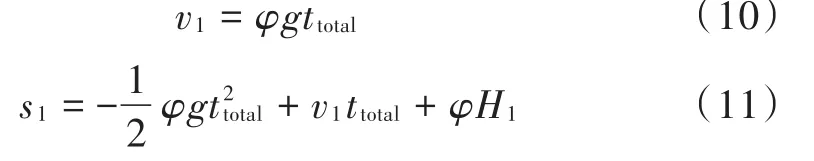
联立式（10），式（11）得：

因此骑车人抛出速度与其抛距关系为：

同理可得电动自行车抛出速度与其抛距关系为：

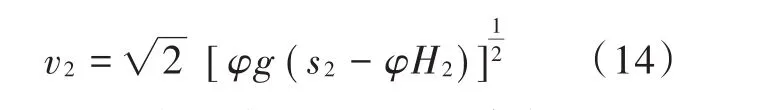
式中：v2为电动自行车抛出速度（单位：m/s）；s2为电动自行车抛距（单位：m）；H2为电动自行车重心高度（单位：m）。

阶段二：计算大型车碰撞后速度。

设大型车碰撞后滑行距离为L（单位：m），碰撞后速度为v′（单位：m/s），由动能定理可得：

因此，大型车碰撞后速度为：

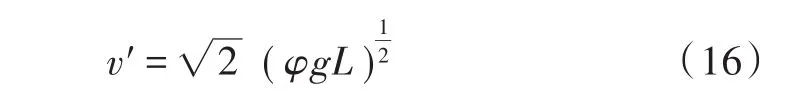
阶段三：计算大型车碰撞速度。

设大型车质量为M（单位：kg），碰撞速度为v（单位：m/s）。由大型车行驶方向上动量守恒可得：

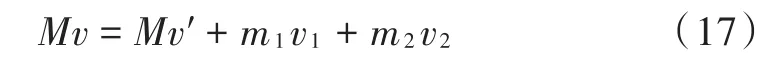
因此，联立式（13），式（14），式（16），式（17）可得大型车碰撞速度为：

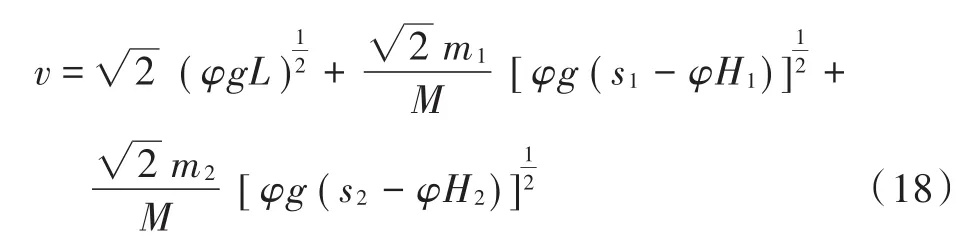
阶段四：计算大型车制动时刻速度。

设大型车制动时刻速度为v0（单位：km/h），路面的附着系数为φ，碰撞前制动距离为d（单位：m），制动时，轮胎与地面的摩擦力做功，大型车的动能转化为轮胎与地面的内能，可得：

联立式（18），式（19）可得：

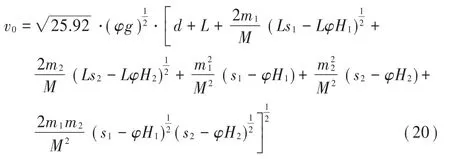
式（20）即为大型车超速辨识模型（OILV），其输出值为大型车制动时刻速度。

2 基于BP神经网络的大型车超速辨识模型优化

2.1 基于四阶段法的大型车超速辨识误差来源分析及优化

在实际事故分析中，碰撞前制动痕迹长度被认定为大型车碰撞前制动距离。而制动痕迹长度小于实际制动距离。如图2所示，大型车在D点开始产生减速度，行驶l后到达E点，减速度达到最大并产生制动痕迹。

图2 开始制动点与制动痕迹产生点差异图Fig.2 Image of difference between starting brake point and brake trace point

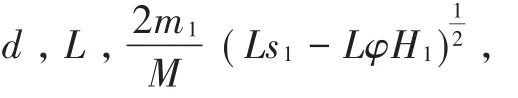
2.2 基于BP神经网络的α值确定

由式（22）变换可得调节因子αs的表达式：

由式（23）可知，α与集合可以作为神经网络的映射。由于BP神经网络具有很好的自学习能力，且较其他神经网络具有一定的容错能力，因此本文利用BP神经网络确定碰撞前制动距离调节因子α，对OILV进行优化。

α作为神经网络输出参数。本文神经网络结构如图3所示。

隐含层节点个数的确定可参考式（24）：

式中：n1为隐含层节点个数；n为输入层节点个数，n=10；m为输出层节点个数，m=1；a为[1，10]之间的整数。

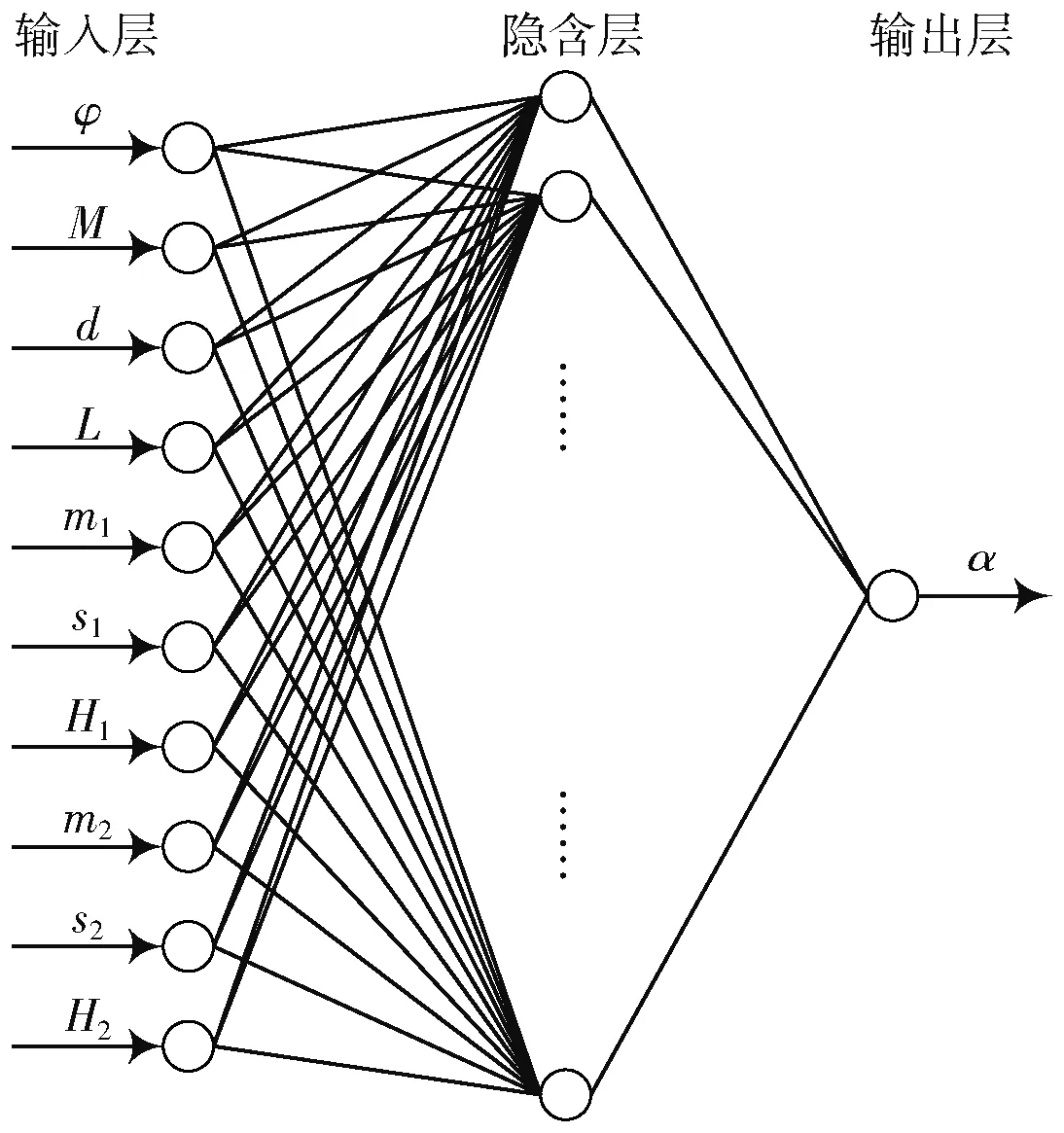
图3 本文神经网络结构图Fig.3 Structure diagram of the proposed neural network

3 基于BP神经网络的大型车超速辨识精度验证

3.1 实验环境设置

本文采用PC-Crash 8.0版本进行验证样本采集。

设定PC-Crash输入集合input={φ,M,d,m1,H1,m2,；输出集合output={L,s1,s2}。

本文利用PC-Crash进行实验。每次实验首先在取值范围内随机产生输入参数，如表1所示；继而得到与之对应的输出参数，从而获得1个样本。本文共实施200次实验总计获得200个样本：

表1 input各参数取值区间Table 1 Value interval of each input parameter

在表1中，附着系数反映了不同状态下地面的摩擦力，区间[0.5，0.6]反映的为潮湿路面，区间[0.6，0.7]反映的为半干燥路面，区间[0.7，0.8]反映的为干燥路面。当大型车的速度低于30 km/h时，大型车驾驶员有足够的反应时间做出避让措施，使得碰撞事故发生的概率大大降低。同时在城市道路中，由于交通环境限制，其速度超过70 km/h的概率较小。因此，本文将大型车制动时刻速度取值区间设定为[30，70]km/h。同时由于大型车垂直撞击电动自行车不会使得骑车人在其骑行方向上产生偏移，对骑车人的抛距没有影响，因此将电动自行车速度设定为0。

3.2 BP神经网络隐含层节点数的确定

从Ui,i∈[1,200]中随机抽取100组样本组成Yi,i∈[1,100]，得出神经网络训练样本：

剩余的100组样本组成Yi,i∈[101,200]，得出测试样本：

本文利用训练样本训练神经网络，继而使用训练好的神经网络分别针对训练样本和测试样本进行验证，输出不同的α值，根据式（22）计算v0，并与标准值对比计算误差。

本文首先通过对比不同隐含层节点数下神经网络训练样本辨识自验证和测试样本辨识精度以确定最优的隐含层节点数。不同隐含层节点数下的训练样本辨识误差和测试样本辨识误差对比如表2所示。

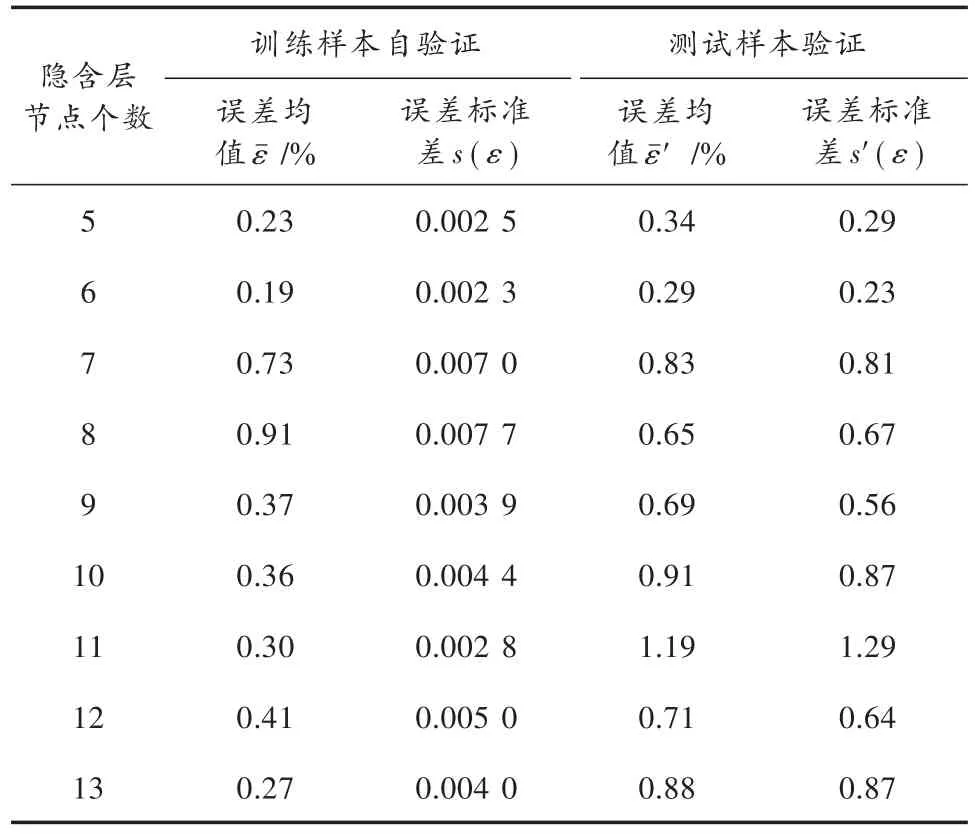
表2 不同隐含层节点的BP-OILV超速辨识精度对比Table 2 Comparison of BP-OILV overspeed identification accuracy for different hidden layer nodes

由表2可知，当隐含层节点数为6时，BP-OILV的误差最小，且超速辨识精度更稳定，因此本文将神经网络隐含层节点数确定为6。

3.3 BP-OILV辨识精度分析

将测试样本Di及其对应的αi,i∈[101,200]分别输入BP-OILV模型和OILV模型，两种模型超速辨识精度对比如图4所示。

图4 优化前后辨识误差对比Fig.4 Comparison of identification errors before and after optimization

图4中，在100组测试样本验证中，仅有1组样本对应的BP-OILV超速辨识误差超过1%（当v0si=47.21km/h时，误差为1.34%），其余测试样本误差均小于1%；BPOILV将误差均值由OILV下的1.99%降至0.29%，误差标准差由0.011降至0.002。当v0si=31.83km/h时，BPOILV的辨识精度最高，误差由OILV下的3.17%降至0.01%；当v0si=39.92km/h时，BP-OILV的优化效果最好，误差由OILV下的4.24%降至0.17%。综上，与OILV相比，BP-OILV超速辨识精度更高更稳定。

4 结 论

超速辨识精度直接影响交通事故责任的判定，以及城市交通安全。本文分四阶段逆向还原大型车制动时刻速度，提出基于四阶段法的大型车超速辨识模型，并利用BP神经网络进行优化，提出基于BP神经网络的大型车超速辨识模型，可精确稳定地用于大型车超速辨识。