船用发电机振动分析与结构优化

王 星，孙方旭，王 东，张贤彪，余锡文



船用发电机振动分析与结构优化

王 星，孙方旭，王 东，张贤彪，余锡文

（舰船综合电力技术国防科技重点实验室（海军工程大学），武汉 430033）

针对船用发电机的结构开展了一系列的结构振动分析和结构优化工作。通过振动测试、实验模态分析和有限元仿真的结果对比，定位了结构振动突出的产生原因，并验证了整改措施的可行性。本文总结了刚性电机转子设计、端盖配合、机座结构设计的经验，为类似电机的声振结构优化设计提供指导。

船用发电机结构振动；结构优化；有限元仿真；实验模态分析

0 前言

当前，电机作为各型装备中的重要振动源，减振降噪的需求突出，其振动噪声性能往往成为电机产品性能优劣的重要指标。减振降噪的手段包括源头减振、结构修改、隔振、吸振、阻尼减振[1]。就电机本体而言，主要有源头减振、结构修改和阻尼减振。除去电磁方案和电机控制相关的电磁激励源抑制措施，其它涉及结构方面的减振手段，都可以归纳为电机的声振结构优化范畴。

结构优化问题可以分为材料参数优化、尺寸优化、形状优化和拓扑优化[2]。材料参数优化以结构的材料参数，如杨氏模量、阻尼、密度等进行自由设计。尺寸优化和形状优化均以结构的尺寸参数为变量进行优化，优化过程都没有改变结构的连接方式。而拓扑优化不同，被认为是最具有自由度的设计手段，区别于一般的结构优化目标，例如重量、刚度（或柔度）、强度、热学特性。为了实现减振降噪目的，电机的声振结构优化目标包括：固有特征频率优化和动力响应最小或传输损失最大。针对电机这样的复杂结构，一般辅以有限元（FEM）或边界元（BEM）实现模型建模，配合相应的尺寸、重量、材料库等约束条件，完成优化设计。文献表明，电机结构设计的一个重要工作是固有特征频率设计，避免与激励源发生共振。而在利用拓扑优化实现振动能量传输损失最大化方面，还缺少完整的案例分析。

以上结构优化问题都属于宏观的确定性优化问题，没有考虑加工制造、装配或测量等微观尺度引入的随机误差。相关经验表明，装配过盈量、螺栓预紧力等随机因素对振动的影响不可忽视。针对这一问题，学术界发展了基于随机性或可靠性的结构优化方法。

本文针对某船用发电机出现的振动问题，通过振动测试、实验模态分析、有限元仿真分析等手段，对相关振动问题进行定性。采用尺寸优化、拓扑优化手段对电机转子、机座结构进行改进设计。此外，针对随机出现的半频振动现象，开展了定性分析和实验验证。

1 问题描述

某发电机额定工作转速1800r/min，采用电动机法运行测试，低频段机脚垂向振动平均频谱如图1所示。

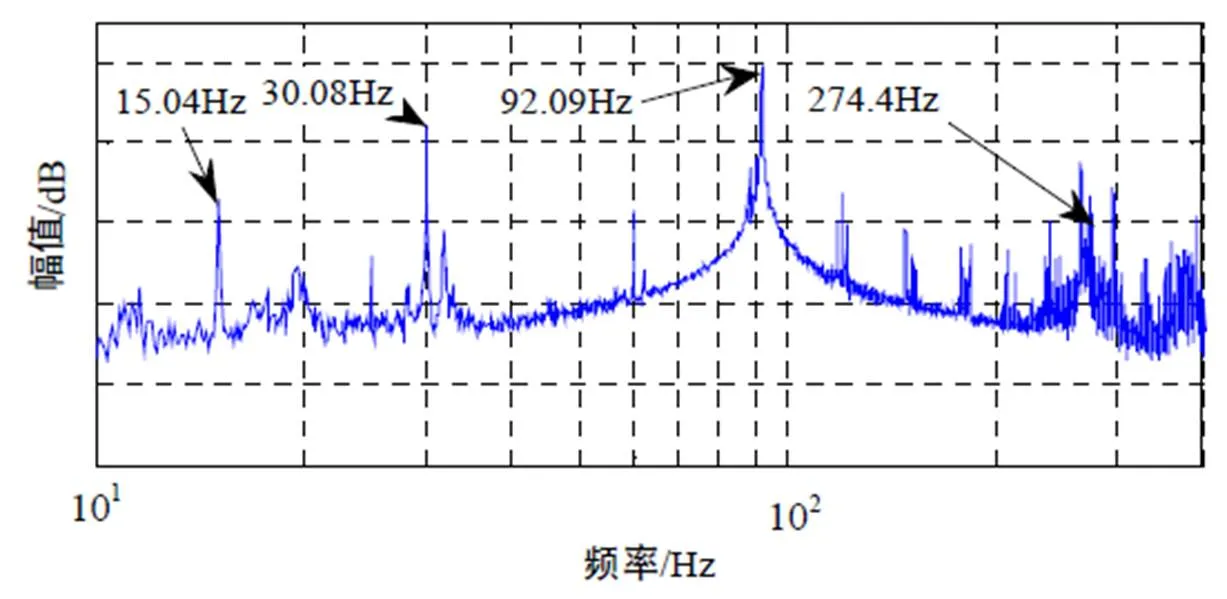
图1 机脚振动频谱（1800r/min）（纵坐标刻度间隔为10dB，下同）

从图1可以看出，低频段，机脚振动主要特征为低频线谱和共振峰，具体现象为：

（1）15.04Hz，工作转频的半频；

（2）30.08Hz，工作转频，单根线谱突出，主要原因为转子质量不平衡，现场动平衡残余量越小，振幅越小；

（3）92.09Hz，三倍转频附近宽频振动峰；

（4）274.4Hz，宽频振动峰。

由于转频振动主要和不平衡量相关，可以通过控制加工制造精度来提高动平衡等级抑制，这里不做详细论述。下面将分别分析半频、3倍频及274Hz附近振动峰产生的原因。

2 半频振动问题定性分析

在一次拆端盖检查后，将轴承端盖换一个角度重装。测试结果表明，半频振动（15Hz）的出现具有随机性。一方面，对比图1和图2，重装后1800r/min测试半频振动消失；另一方面，详见图3，重装端盖后变转速运行，在转速1500r/min出现半频成分（12.5Hz），其它转速（1200r/min，1680r/min，1800r/min）半频成分消失。

图2 机脚振动频谱（端盖重装，1800r/min测试）

通常半频、三分之一倍频等亚谐频振动与非线性因素有关，比如油膜轴承支撑转子的非线性油膜力、转子与定子碰磨、转子支撑件松动、转子裂纹[3]。通过端盖重装对比，初步怀疑半频振动与支撑端盖止口、机座止口的配合松动相关。在调试阶段，电机经过多次拆装，端盖与机座间配合形式可能由设计的过渡配合变为间隙配合。

3 三倍频附近振动峰问题分析与定性

如图1所示，由于三倍频附近频率主峰92.09Hz不是严格的3倍转频，且90Hz处有一个幅值较低的振动峰，形成双振动峰。因此，不能将此问题直接归为3倍频激励因素。

下面分别从源头、变转速运行、模态振型、仿真等方面进行分析。

3.1 激励源分析

转子系统的响应问题本质是不平衡力激励下的强迫振动响应问题，激励频率为转子工作频率。以单元盘转子为例，假设存在二次、三次非线性项，则偏心质量引起的转子运动方程可疑描述为[3]：

该转子的响应将不仅包含项，还有2、3频率成分，且高次分量成分的激励形式与质量偏心激励一样。二次、三次非线性项与非线性油膜力、材料内阻、滚珠动静摩擦等非线性因素有关。

假设激励频率与转子系统固有频率有微小失调，=n+，为微小常量，为失调参数。在非线性因素作用下，系统受迫振动的幅频响应和相频响应特性区别于线性系统共振，即幅频响应主振动峰将偏离固有频率。这也是3激励下的转子响应峰值偏离90Hz的原因。

3.2 振动测试

如图3所示，变转速运行实验表明，在90~100Hz之间，存在一个相对不动的宽频主峰，峰值97Hz左右。当该范围内有3倍（1800r/min，90Hz）、4倍（1500r/min，100Hz）或5倍（1200r/min，100Hz）转频时，该主振峰振幅明显偏高。相反，在1680r/min时，3倍频84Hz和4倍频112Hz均不在该频率区间，对应的主振峰频率（97.7Hz）的幅值比其它转速的峰值低10dB以上。

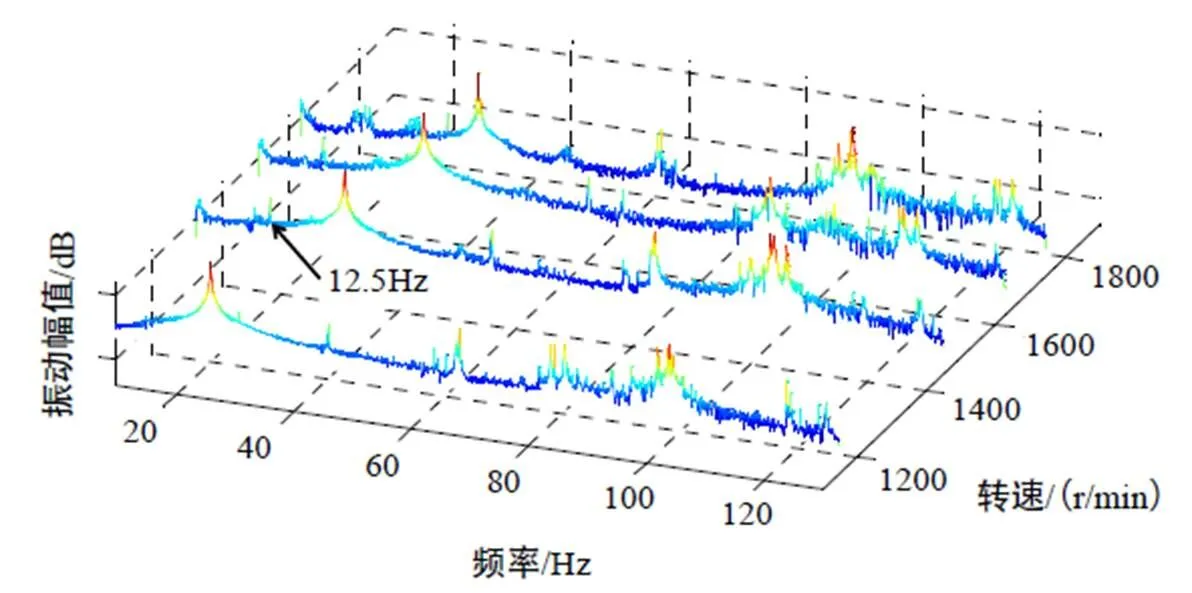
图3 变转速运行机脚频谱

图4 机脚振动频谱（1680r/min）

因此，推测区间90~100Hz内的主振峰为模态共振峰，在1800r/min的3倍转频激励下，产生了92.09Hz左右的宽频响应。在电机上共布置20个测点，如图5所示。1800r/min下各测点在92.09Hz处振动相位见表1。从振动相位特征看，机脚测点11、12、13、14与机座测点6、19、20、10近似同相位。这说明，在92.09Hz机脚垂向、机座垂向、端盖垂向的模态振型为同相位垂向共振。

图5 各测点布置图

表1 三倍频附近峰值点的幅值和相位分布

3.3 实验模态分析

为了进一步确定机座整体的模态分布特征，采用BK模态测试系统，实测整机在98.5Hz处存在模态，且模态振型为机座整体垂向共振，如图6所示，这与前面相位分析结果一致。

图6 实验模态测试的98.5Hz模态振型

3.4 有限元仿真分析

经过前面分析，基本可以确定92.09Hz振动峰除了激励源的因素，还存在结构模态共振。但是，从振型上，很难解释共振形成的机理。这里采用Ansys17.0建立整机的有限元模型，每个隔振器采用三个互相垂直的弹簧代替，弹簧刚度设置为隔振器的实际的三个方向的动刚度。按照经验处理办法，忽略滚珠轴承的阻尼。由于滚动轴承参振质量较小，忽略轴承的质量。因此，滚动轴承简化为弹簧。在很多文献中提到，由于轴承间隙和滚珠接触位置变化引起轴承刚度周期变化，滚动轴承刚度为非线性刚度，表现为参数激振（VC振动）[4,5]，但从结果看，这种由于滚珠接触位置变化带来的相对刚度变幅基本可以忽略[6]。因此，在Ansys Workbench仿真模型中，将滚动轴承设置为刚度为常数的弹簧，采用bushing单元建模，定义轴承的径向、轴向的等效动刚度。刚度系数xxyy，kxy=kyx=0，刚度系数常用取值为2×107~1×108N/m[7]，模型中取1×108N/m。

仿真结果表明，94.4Hz处存在转子-机座耦合共振模态，该振型是由转子一阶弯曲模态振动带动定子、机座做垂向振动，如图7所示。振型仿真结果也与振动测试、模态测试的结论一致。

(a) 整机振型

(b) 转子振型

图7 94.4Hz模态仿真结果

3.5 小结

通过以上分析，可以确定三倍频附近存在转子一阶弯曲与机座耦合的共振模态，该模态在非线性因素作用下，被3倍转频激励共振，机座整体表现出垂向振动振型。

4 274Hz振动峰问题定性

通过振动测试、模态测试和仿真分析，同时可以确定274Hz振动峰的产生原因和机座模态振动相关，仿真振型如图8所示。由于非伸端出线盒开口位置与通风孔位置太近，造成非伸端整体刚度变差，非伸端存在整体扭曲的模态。尽管没有明显的激励，但在背景激励下，该模态导致的宽频率响应高。

图8 275.4Hz机座模态仿真振型

下表2为汇总了低频段隔振器刚体模态、转子一阶弯曲与定子耦合模态、机座非伸端模态的测试、仿真、数值计算结果。其中，数值计算结果来自基于模态综合法的转子-机座耦合计算。仿真结果与实验测试结果误差小于5%，证明了仿真模型的准确性，为后续改进方案验证提供了模型参考。

表2 部分低频模态的仿真计算与测试结果对比

5 转子系统结构优化与实验验证

根据前面分析，为了降低三倍频附近振动，必须修改转子-轴承系统，将耦合模态从92.0Hz提高到105~110Hz左右，避开三倍频（90Hz）和四倍频（120Hz）激励。图9所示为转子系统的结构优化措施汇总。

图9 转子系统结构优化措施

提高转子系统一阶弯曲模态有以下几方面措施：

（1）增大轴承座支撑刚度。这里首先进行了工艺验证，重新加工了一套端盖，增加径向加强筋，如图9所示。同时，新端盖止口与机座止口配合方式做了改变，原端盖为过渡配合，新工艺验证端盖为过盈配合，并且要求装配完成后尽量减少电机端盖的拆装。工艺验证试验表明，并没有明显提高共振频率，即加筋对端盖等效刚度提高不明显。但三倍频附近振动峰值下降10dB以上（相对图1），这说明端盖止口配合工艺，只是增大了转子系统的接触阻尼。共振模态频率依然不变，问题的本质并没有解决。

（2）增大轴承安装预紧力。轴承等效支撑刚度与预紧力相关，预紧力越大，等效支撑刚度越大。实际轴承的安装工艺尺寸已经在出厂时确定好，不适合在增加。

（3）转轴结构优化设计

通过以上分析，为了提高转子机座耦合系统的模态，最主要的措施为修改转子本体结构，可行的修改措施，如图9所示。

该结构优化问题属于尺寸参数优化，目标函数为转子一阶弯曲模态与目标频率（105Hz）的差值最小化。约束条件分别为：耦合系统的转子一阶弯曲模态约束，轴段的半径约束R1、R2，伸端轴段的长度约束1、2。转子结构优化的数学描述为：

min {|1-105|}

s. t. :

λ2=ψTKψ，=1，2，3…

I=ψTMψ，=1，2，3…

R1≤R≤R2，=1，2，3

1≤≤2

其中，λ为耦合系统的各阶模态频率，ψ为耦合系统的正则模态，K为正则刚度，I为对角单位矩阵。模态频率计算模型可以是数值建模方法，比如基于模态综合法或阻抗匹配法建立的耦合系统运动模型，也可以是仿真分析方法。通常需结合寻优算法进行快速求解。这里因为模型简单，采用等间隔遍历计算也可快速求解转子合适的尺寸参数。

样机整改后，机脚的振动频谱如图10所示。通过对比图1，三倍频附近的模态共振峰转移到108.9Hz，并且由于避开了三倍、四倍转频，振动峰值明显降低（参考图1）。从图10也可以发现，由于非线性因素，3倍频激励峰值仍为92Hz，但幅值显著降低。

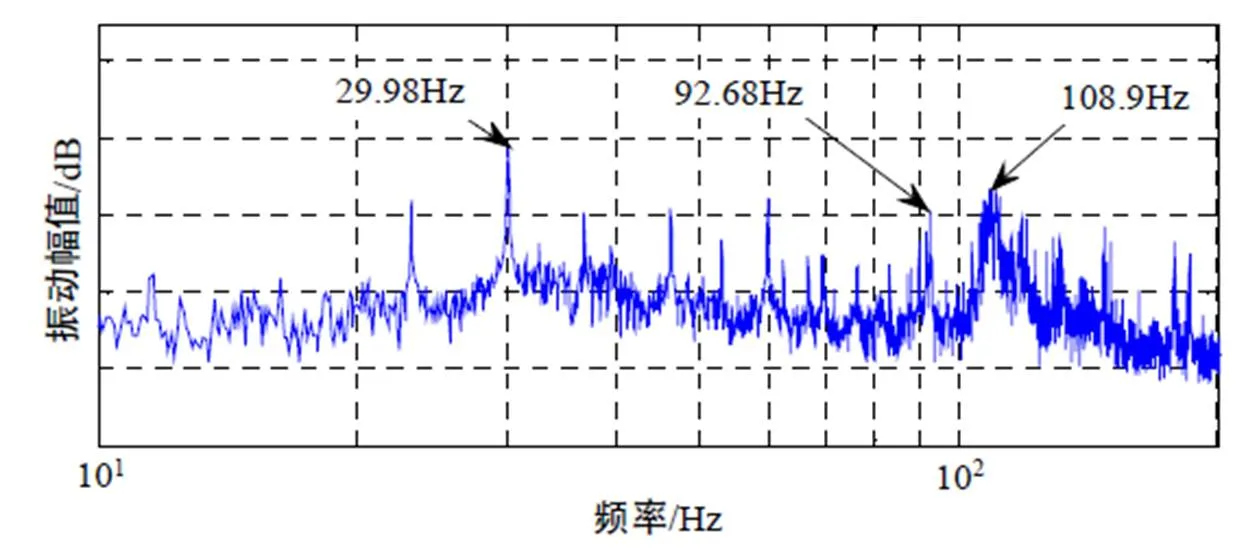
图10 样机整改后，机脚测试频谱（1800r/min）

6 机座结构优化与实验验证

根据第4节振动问题定性，机座非伸端由于出线盒位置与侧面开窗位置集中，造成的局部刚度较差。需要对侧窗和出线盒位置进行优化，这属于结构拓扑优化范畴。由于侧窗的作用是布线和配重，不能更改，因此，只能优化出线盒位置。目标函数为非伸端局部弯曲模态的特征频率最大化，约束条件包含模态振型、出线盒位置。数学模型参考转子结构。由于机座两端都有侧窗，这里采用近似经验处理办法，将出线盒移动到中间靠近伸端侧。整改后的数据表明，274Hz没有明显共振峰，250Hz频段有20dB的安全余量。

7 结论

（1）本文介绍了电机的结构优化类型，结合某发电机结构整改工作，开展了详细说明，为后续电机结构优化提供了理论指导。

（2）重点针对3倍转频附近振动突出问题，开展了充分的实验、仿真和计算分析。根据变转速实验测试结果，刚性电机转子的一阶临界转速设计也应避开转频和低阶倍频。初步指出转子系统的非线性因素作用力与该模态共振现象有关，但在共振形成机理方面，还需开展深入研究。

（3）通过对比验证实验，定性地总结了装配公差对转子支撑系统的等效阻尼有影响。

[1] 盛美萍, 王敏庆, 孙进才. 噪声与振动控制技术基础[M]. 北京: 科学出版社, 2001.

[2] 杜建镔. 结构优化及其在振动和声学设计中的应用[M]. 北京: 清华大学出版社, 2015.

[3] 李录平, 卢绪祥. 汽轮发电机组振动与处理[M].北京: 中国电力出版社, 2007.

[4] 陈果. 转子-滚动轴承-机匣耦合系统的不平衡碰磨耦合故障非线性动力学响应[J]. 航空动力学报, 2007, 22(10):1771-778.

[5] 陶海亮, 潘波,等. 滚动轴承-转子系统非线性动力学响应分析[J]. 燃气轮机技术, 2013, 26(1):15-20.

[6] 曹宏瑞, 李亚敏, 何正嘉,等. 高速滚动轴承-转子系统时变刚度及振动响应分析[J]. 机械工程学报, 2014, 50(15):73-81.

[7] 钟一锷. 转子动力学[M]. 北京: 清华大学出版社, 1987.

The Analysis on Structural Vibration and Optimization of Marine Generator

WANG Xing, SUN Fangxu, WANG Dong, ZHANG Xianbiao, YU Xiwen

(National Key Laboratory of Science and Technology on Vessel Integrated Power System(Navy University of Engineering), Wuhan 430033, China)

A set of analysis on structural vibration and structural optimization are carried out on a generator. By comparing the results from vibration test, experimental modal analysis and finite element analysis, the reasons causing vibration peaks are located, and the solving measures are verified to be feasible. This work concludes the design experience on rigid rotor critical speed, fit tolerance of end-shield and structural topology of stator frame, which provide guidance for the structural optimization design of motors with similar structure.

marine generator structural vibration; structural optimization; finite element simulation; experimental modal analysis

TM301.4+2

A

1000-3983(2018)05-0001-05

2018-05-26

王星（1987-），2015年毕业于英国利物浦大学，博士，从事电机减振降噪和结构优化设计，助理研究员。

国家自然科学基金（51707202，51707201，51807201）