基于完备循环差集的type-Ⅱ QC-LDPC码的构造
黄 胜, 宋 静, 袁建国
(重庆邮电大学光通信及网络重点实验室, 重庆 400065)
0 引 言
低密度奇偶校验(low-density parity-check, LDPC)码[1]是线性分组码的一种,因其性能良好,广泛应用在许多领域。2016年,LDPC码作为5G的标准码重新引起世人的关注,对于准循环(quasi-cyclic)低密度奇偶校验(quasi-cyclic low-density parity check,QC-LDPC)码[2]来讲,若校验矩阵H仅由单位循环置换矩阵(circulant permutation matrices, CPM)或零矩阵(zero matrices, ZM)构成,其对应的码字为type-I QC-LDPC码[3],多数文献中构造的码都属于type-I QC-LDPC码[4-7]。若校验矩阵中不仅包含ZM、CPM,还含有权重为2的循环置换矩阵(weight-2 circulant permutation matrices, W2-CPM),其对应码字为type-Ⅱ QC-LDPC码,其最小距离的上界值比type-I QC-LDPC码的更大(任意(J,L)规则type-I QC-LDPC码最小距离上界值为dmin≤(J+1)![8],而type-Ⅱ QC-LDPC码的最小距离上界值为dmin≤(J+1)!2J[9])。最小距离又与码的检、纠错能力息息相关,最小距离值越大,码的检错、纠错能力越强。由于type-Ⅱ QC-LDPC码中仅含权重为2的循环矩阵W2-CPM,导致Tanner图中更易出现短环,影响译码性能,出现错误平层。文献[10]主要分析了type-Ⅱ QC-LDPC码中的W2-CPM对最小距离上界值以及译码性能的影响。文献[11]基于sidon序列构造的type-Ⅱ QC-LDPC码,其校验矩阵H中仅包含W2-CPM,Tanner图中含有大量的6环导致译码性能下降。文献[12]基于完备循环差集构造的type-Ⅱ QC-LDPC码,其校验矩阵是满秩的且包含ZM、CPM和W2-CPM的3种形式的子矩阵,校验矩阵具有中心对称结构,围长至少为8,但由于8环的数量过多影响了译码性能。文献[13]基于有限域构造的type-Ⅱ QC-LDPC码的校验矩阵同样包含ZM、CPM和W2-CPM子矩阵,但文中并未给出具体的仿真实验结果,而仅有理论分析。文献[14]基于完备循环差集,构造了一种新颖的可快速编码的非规则type-Ⅱ QC-LDPC码,但因其含有短环,影响了迭代译码收敛速度,导致迭代译码性能下降。
基于此,本文构造一种type-Ⅱ QC-LDPC码,其围长至少为8,且8环的数量较少,迭代译码性能优异。首先构造校验矩阵H,校验矩阵具有近似双对角的结构,再由完备循环差集填充,用CPM、ZM和W2-CPM的矩阵扩展校验矩阵H,通过推理证明校验矩阵中不含4、6环。由仿真实验结果可知,在迭代译码时,本文构造的type-Ⅱ QC-LDPC码无明显的错误平层。
1 完备循环差集
定义1设v为正整数,取加法群Zv={0,1,2…,v-1}中的t个子集,每个子集包含k个元素,即Di={d1,d2,…,dk},i=1,2…t,m≠n,m,n=1,2…k,满足Zv中每个非零元素在(dm-dn)modv运算时,其值恰好出现λ次,则集合Di被定义为一组t-(v,k,λ)循环差集(cyclic difference families, CDF)[15]。当循环差集参数为t=1,λ=1,v=k2-k+1时,称为完备循环差集[14],完备循环差集的特性,即Di中的任意两个元素dm、dn,作(dm-dn)modv运算其值各不相同。对于(7,3,1)-完备循环差集,D={0,1,3}的差集表如表1所示[16]。在差集表中,除0元素外,其余元素具有相异性。
表1 完备循环差集{0,1,3}mod7的差集表
Table 1 Difference table of mod 7 pefect cycle difference family {0,1,3}

2 Type-Ⅱ QC-LDPC码
设J,L,p为正整数,则码长为N=Lp,Type-Ⅱ QC-LDPC码校验矩阵H的结构如式(1)所示[17]。
(2)
3 基于完备循环差集的Type-Ⅱ QC-LDPC码
3.1 构造方法:
基矩阵的构造过程如下所示:



图1 构造的基矩阵E的结构Fig.1 Structure of constructed base matrix E
步骤2令扩展因子为p,大小等于差集的模p=v,将基矩阵E中元素对分别替换为p×p大小的矩阵,权重为2的循环矩阵I(dm)+I(dn),用大小为p×p的单位矩阵替换基矩阵的0元素,用p×p的零矩阵0替换∞元素,从而获得校验矩阵。
通过以上步骤构造出基矩阵,既保留了Type-Ⅱ QC-LDPC码最小距离上界值大的优点,同时利用构造的近似双对角结构与完备循环差集的特性结合,避免了短环的出现,而且构造出的码字具有良好的检、纠错性能。
3.2 围长分析

(3)
满足jn=j0,ln=l0,t2n=t0,当jk=jk+1时,t2k≠t2k+1;当lk=lk+1时,t2k≠t2k+2。
3.2.1 无四环证明
引理1对于所有j0、j1,0≤j0≠j1≤J,所有l0、l1,0≤l0≠l1≤L-1,以及所有ti∈{1,2},0≤i≤3,当以下不等式全部都不成立时,本文构造的校验矩阵H所对应的Tanner图中不存在4环。

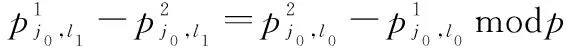


其中,0≤j0,j1≤J, 0≤l0,l1≤L-1,而当l0=l1且j0=j1时,t1≠t0。由完备循环差集的特性可知,基矩阵E中的任意两元素之差作模p运算,值各不相同,因此本文构造的基矩阵不存在4环。
3.2.2 无六环证明
由环长存在定理可知,当n=3时,可将式(3)写为式(4)形式。
(4)
结合基矩阵的结构,可能存在6环的情况如下:
(1) 当j0≠j1≠j2,l0≠l1≠l2时,只有横跨三行三列,才可能出现6环,如图2(a)~图2(f)所示,即如同Type-I QC-LDPC码六环的证明情况一样。由于本文构造的基矩阵有类似双对角结构,结合完备循环差集的特性,基矩阵中的任意两元素之差作模p运算值各不相同,故上述6环情况不会出现。

图2 基矩阵E(H)中6环的存在形式Fig.2 Form of six cycles in E(H)
(2) 当j0=j1,l0=l1时,其他变量保持不变,则式(4)变为式(5)。
(5)
由环长的构成可知,一个环内只有首,尾位置的坐标相同,其余位置不同,而式(5)与之矛盾,故无6环。同理,j0=j1,l2=l1和j0=j1,l2=l0的证明与上述相同。
(3)当j0=j1时,其他变量保持不变,横跨两行三列的形式,则式(4)变为式(6),若6环存在,则如图2(g)所示。
(6)
由图1可知,本文构造的基矩阵中并不存在此结构,故无6环。同理,j2=j1,j2=j0时的证明与上述相同。
(4)当l0=l1时,其他变量保持不变,横跨三行两列的形式,则式(4)变为式(7),若6环存在,则如图2(h)所示。
(7)
由图1可知,本文构造的基矩阵中并不存在此结构,故无6环。同理,l2=l1,l2=l0时的证明与上述相同。
(5)当l0=l1=l2时,其他变量保持不变,三行一列的形式,则式(4)变为式(8),若6环存在,则如图2(i)所示。
(8)
由图1可知,本文构造的基矩阵中并不存在此结构。故无6环,等式(8)不成立。
(6)当j0=j1=j2时,其他变量保持不变,一行三列的形式,则式(4)变为式(9),若6环存在,则如图2(j)所示。
(9)
由图1可知,本文构造的基矩阵含有此结构,又因为完备循环差集中任意两元素之差作模p运算值各不相同,故等式(9)不成立。综上所述,本文构造的基矩阵中不含6环。
4 仿真与性能分析
在构造QC-LDPC码时,需要考虑码的结构、码长、码率等影响性能的因素。一般来讲,当其他参数相同的情况下,码长较长时,性能普遍好。但码长过长会导致时延增加。码率越小,纠错性能越好,但会导致监督位的过度冗余。本文构造中短码长,码率为0.5的码字。采用加性高斯白噪声(additive white Gaussian noise, AWGN)信道,和积(sum-product algorithm, SPA)译码,BPSK调制,选择迭代50次。
首先选取完备循环差集为{1,2,23,34,84, 123,136,142,146,160,176,201,226,230,232,239},将完备循环差集的元素分为h={1,2,23,34,84,123,136,142},g={160,176,201, 226,230,232,239}两个子集,令δ=5,μ=3,h*={123,136,142,1,2,23,34,84},g*={201,226,230,232,239,146,160,176},令p=241,码率为R=0.5,码长N=3 856。

图3 码率为0.5的Type-Ⅱ P-CDF-QC-LDPC (3 856,1 928)码与其他码型的纠错性能对比图 Fig.3 Contrast figure of error correction performance of Type-Ⅱ P-CDF-QC-LDPC (2 680,1 340) code at code-rate of 0.5
本文构造的基于完备循环差集的围长至少为8的type-Ⅱ P-CDF-QC-LDPC(3 856,1 928)码,与文献[14]基于完备循环差集构造的非规则且可实现快速编码的type-Ⅱ CDS-QC-LDPC(4 788,2 394)码比较,同时与文献[17]基于完备循环差集构造的列重为4的规则type-Ⅱ P-CDS-QC-LDPC (3 906,1 953)码的性能进行比较,在误码率为(bit error ratio, BER)为10-6时,其净编码增益分别提高0.42 dB和0.15 dB。
为进一步展现构造码字的优越性能,构造码率为0.5,码长为6 096的type-Ⅱ P-CDF- QC-LDPC(6 096,3 048)码,选择完备循环差集{1,2,20,29,97,119,152,154,177,203,241,255,291,297,301,308,338,362,367,370},令δ=5,μ=3,p=381,将构造的码字分别与基于sidon序列构造的type-Ⅱ QC-LDPC码,基于斐波那契数列构造的type-I QC-LDPC码对比,如图4所示。

图4 码率为0.5的Type-Ⅱ P-CDF-QC-LDPC(6 096,3 048)码与其他码型的纠错性能对比图 Fig.4 Contrast figure of error correction performance of Type-Ⅱ P-CDF-QC-LDPC (6096,3048) code at code-rate of 0.5
在BER为10-6时,与文献[11]基于sidon序列构造的type-Ⅱ SD-QC-LDPC(6 096,3 048)码和文献[19]基于斐波那契数列构造的type-I FS-QC-LDPC(6 200,3 100)码相比,本文构造的type-Ⅱ P-CDF-QC-LDPC(6 096,3 048)码的净编码增益分别提升0.3 dB和0.4 dB。
综合上述分析,与其他具有优异性能的QC-LDPC码相比,本文type-Ⅱ P-CDF-QC-LDPC码的码率为0.5,围长至少为8,并且具有较为明显的净编码增益。
5 结 论
本文提出了基于完备循环差集构造具有近似双对角结构的type-Ⅱ P-CDF- QC-LDPC码的设计方法,使其对应的Tanner图中的围长至少为8,且8环的数量较少。基矩阵中的元素由完备循环差集中的元素构成,节省了存储空间,该方法构造简单,在高信噪比区域收敛速度快速,无明显的错误平层,其纠错性能优异。

