基于粗糙Choquet 积分的产品服务系统设计方案优选
邱华清 耿秀丽 徐轶才
上海理工大学管理学院,上海,200093
0 引言
目前,我国制造业发展面临着环境污染、能源利用率低以及国际竞争力弱等多方面的问题。为提高企业可持续发展能力,不再仅将服务作为产品的附属要素,而是通过产品和服务的有机融合在产品生命周期内实现价值增值并抢占市场空间,产品服务系统(product⁃service system,PSS)受到越来越多的关注。在概念设计阶段,由于PSS配置优化的多目标性、客户需求的模糊性以及设计工程师对需求理解的不一致性等问题,通常会导致多个可行性方案的形成。如何对PSS设计方案进行合理优选,关系到方案的后续执行以及对顾客需求把握的正确性。PSS方案评价是一种典型的多属性决策问题,应用常见的多属性决策方法时,如逼近理想解排序法(technique for or⁃der preference by similarity to ideal solution,TOPSIS)[1⁃2]、多准则妥协解排序法(VIKOR)[3]、层次分析法(analytic hierarchy process,AHP)和复杂比例评价法[4]等往往忽视了评价指标间存在关联关系的复杂情况,降低了决策结果的准确性。
满足顾客需求是PSS的典型特点,把顾客需求作为评价指标能够将顾客的想法考虑到方案评价过程中,有利于优选出顾客满意的方案。但是顾客需求提出时具有不确定性且并未考虑需求间的关联关系,即可能存在包含、冲突等关系。以顾客需求作为评价指标进行PSS方案评价时,指标间的复杂关系会对方案的选择产生影响。例如,评价一款轿车设计方案的好坏通常会考虑到成本、能耗和服务支持等方面。一般来说,能耗低的车辆成本较高;服务支持内容多的车辆则需要软件硬件系统实时监测,其能耗就较高。在该PSS方案评价过程中,通常较高的指标评价值会对较低的指标评价值起到补偿作用,共同影响最终的评价结果。为增加决策结果的准确性,指标间的相互影响关系不容忽视。常用网络分析法(analytic network process,ANP)和决策试验与实验评估法(decision making trial and evalua⁃tion laboratory,DEMATEL)可以对因素间的关系进行分析。两种方法都是先通过专家主观评价法建立指标间的关联关系矩阵,然后进行矩阵运算得出指标权重或指标间的最终关系矩阵。一方面专家多次主观判断易产生不一致性;另一方面这两种方法对分析存在关联关系的指标权重确定问题有优势,而对指标间存在关联关系的方案评价问题有一定局限。ANP法和DEMA⁃TEL法不能很好地将指标间的关联关系反映到方案评价值的集结过程中。模糊测度用约束条件较弱的单调性和连续性取代了经典概率中的可加性刚性约束,能够很好地描述指标间的任意交互作用[5]。基于模糊测度的Choquet积分算子用来进行人的主观评价和主观行为分析,是分析属性关联行为的有力工具[6]。本文采用Choquet积分算子对方案评价值进行集结,将指标间的关联关系反映到方案评价过程中,对PSS设计方案进行优选。
在不确定性信息处理方面,模糊集理论常应用于多属性决策问题。例如,文献[7]提出了一种模糊随机环境下基于信息公理的PSS方案评价方法,通过计算各方案的信息量进行方案排序。文献[8]从用户的视角出发,采用质量功能展开(quality function deploy,QFD)法计算评价指标权重,然后将直觉模糊数与TOPSIS相结合对方案进行评价。文献[9]将线性规划和TOP⁃SIS结合,对犹豫模糊环境下的多属性决策问题进行求解。模糊集的应用虽然在一定程度上描述了决策过程中的不确定性,但模糊集通常需要设置隶属度函数,隶属度函数的确定则存在一定的主观性和随机性;此外,模糊评价方法也不能很好地体现决策者的经验、知识等对决策不确定性的影响[10]。粗糙集理论是一种新的处理模糊和不确定性信息的数学理论。与模糊数相比,粗糙数不需要外部信息,且不需要隶属度函数、效用函数等先验信息,较大程度地保持了信息的客观性。不同于单一的产品设计方案多为定量评价指标,顾客需求的模糊性使其作为PSS方案评价指标时,包含大量的定性评价信息。本文需要将粗糙数和Choquet积分相结合,通过粗糙数的下限、上限表达评价过程中的不确定性信息,且考虑指标间的关联关系对方案评价的影响进行评价值的集结。
Choquet积分算子已扩展到二元语义、区间二元语义、犹豫模糊数和区间灰数等决策环境,Cho⁃quet积分与粗糙数结合较为鲜见。例如,文献[11]定义了二元语义Choquet积分集结算子,并将其应用于多属性决策问题中。文献[12]基于Cho⁃quet积分研究了评价值为区间二元语义且评价指标间存在关联关系的多属性群决策问题。文献[13]定义了区间直觉犹豫模糊Choquet积分算子,基于Choquet积分与TOPSIS相结合的方法解决了多属性群决策问题。文献[14]针对评价值为区间灰数的情况,定义了区间灰数Choquet积分集结算子,并将其与灰靶决策方法相结合应用于多属性群决策问题。
本文采用粗糙集处理专家评价值,通过粗糙数表达决策不确定性信息;针对评价指标间的关联关系,将粗糙数与Choquet积分相结合并对各方案的评价值进行集结;最后以某PSS方案评价实例来验证所提方法的有效性。
1 理论基础
1.1 粗糙数
粗糙数采用区间数的形式表达不确定性信息,以目标集合的下近似和上近似描述模糊信息。利用专家给出的指标评价数据确定粗糙数的下限和上限而不需要数据的分析调整,有利于决策结果的准确性和客观性。
定义1[15]假设论域U分为n类,表示为R={C1,C2,…,Cn}。如果存在序关系 C1<C2<…<Cn,则∀Ci∈ R,i=1,2,…,n。Ci的下近似域、上近似域分别为

Ci的边界区域定义为
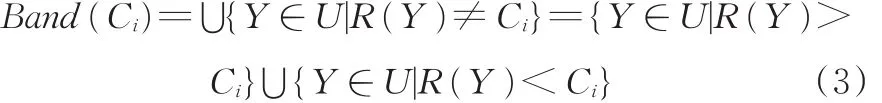
Ci的粗糙数的下限、上限分别为
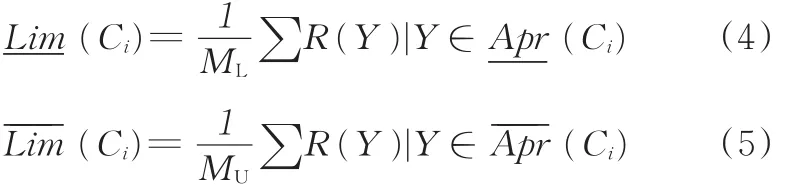
其中,ML和MU分别表示Ci的下近似域、上近似域中对象的数量。则Ci的粗糙数Rmm表示为

粗糙数本质上是区间数,其运算规则与区间数的运算规则相同。设为两个粗糙数,常数 k>0,则2个区间数比较的可能度公式以及基本运算如下[16]:
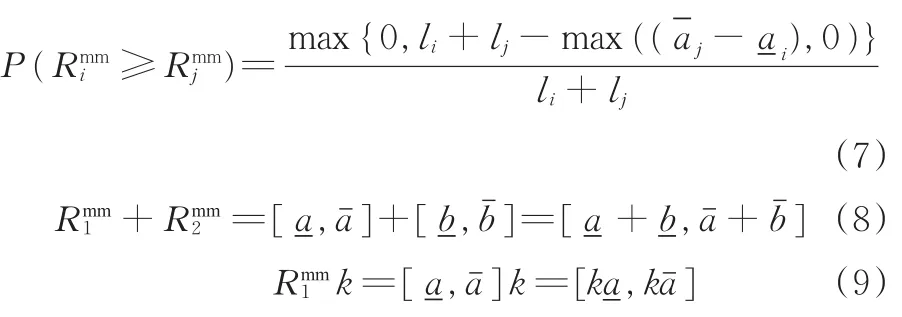
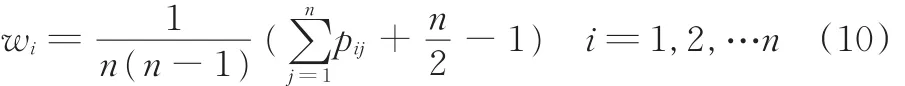
1.2 模糊测度和Choquet积分

若λ=0即µ(A⋃B)=µ(A)+µ(B),则µ为X上的可加测度,表示属性集合A与B间无相互关联关系,A与B是相互独立的;若λ<0即µ(A⋃B)<µ(A)+µ(B),则µ为X上的次可加测度,表示属性集合A与B间有替代作用,A与B间存在信息冗余;若λ>0即µ(A⋃B)>µ(A)+µ(B),则µ为X上的超可加测度,表示属性集合A与B间有相乘作用,A与B间存在信息互补。
利用λ⁃模糊测度可以表达多属性群决策问题中属性间的关联关系,其中属性集即为定义2中的非空集合X,各属性的重要度即为集合X的模糊测度。若有限集合 X={x1,x2,…,xn},∀i,j=则λ⁃模糊测度µ满足:
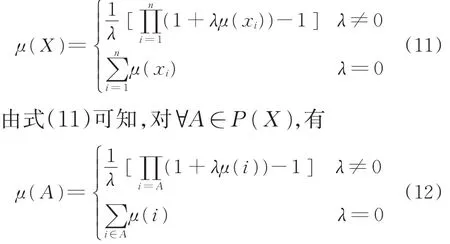
由边际条件 µ(X)=1,根据式(11)和式(12),可由以下方程确定唯一的参数λ:
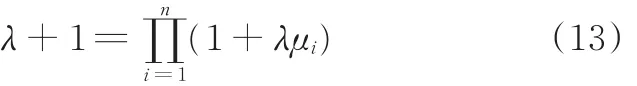

定义3[18]若f为定义在X上的非负函数,µ为定义在X上的模糊测度,则f关于模糊测度µ的离散Choquet积分如下:
2 基于粗糙Choquet积分的PSS方案优选过程
2.1 PSS方案优选框架
PSS设计方案的目标是最大程度地满足顾客需求,通过产品和服务的相互配合获得顾客的最佳使用价值和体验。以顾客需求项作为方案的评价指标,将顾客需求反映到方案评价过程中,可以更好地衡量设计方案满足顾客需求的程度,从而实现PSS设计方案的有效优选。
顾客需求的模糊性和复杂性导致其内部具有交互关系,将顾客需求作为PSS方案评价指标时,需要考虑到指标间的关联关系。模糊测度较好地描述了各指标的相互作用现象,并通过Choquet积分对各方案评价值进行集结,较好地考虑了指标间的关联关系对方案评价结果的影响。针对方案评价过程中的不确定信息,采用粗糙数处理专家评价信息,使评价结果更加客观。本文将粗糙数与Choquet积分相结合,解决了决策过程中的模糊性问题以及评价指标间的关联关系问题,以提高决策结果的科学性、合理性。本文所提基于粗糙Choquet积分的PSS设计方案优选框架见图1。
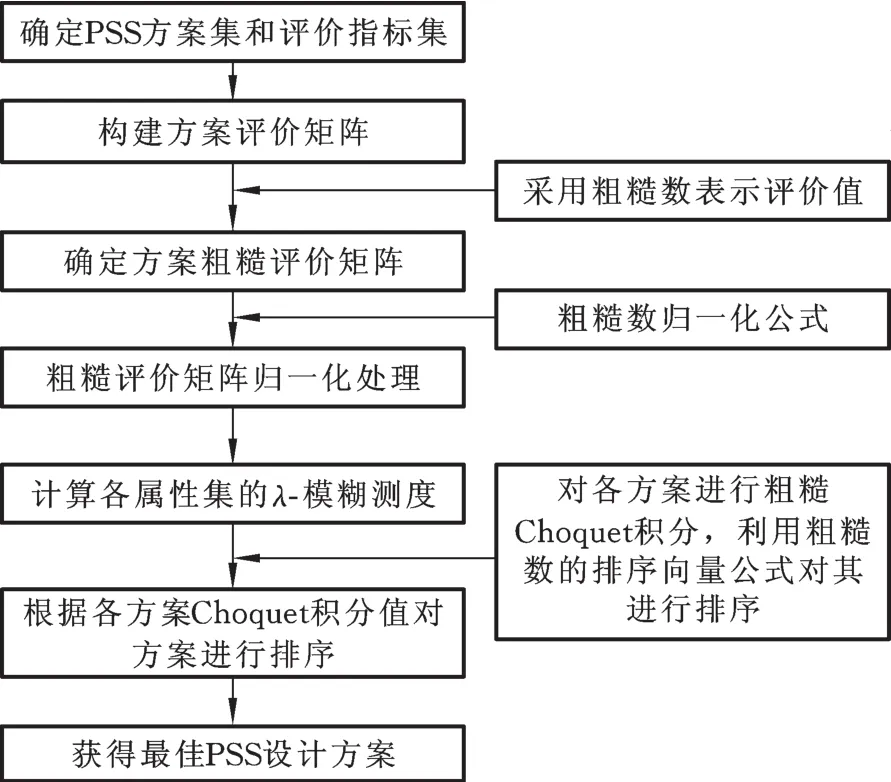
图1 基于粗糙Choquet积分的PSS设计方案优选框架Fig.1 Optimization frame of PSS concept based on rough Choquet integral
2.2 PSS方案优选步骤
假设需要评价的方案为Pi(i=1,2,…,m),评价指标为Cj(j=1,2,…,n),专家Ek(k=1,2,…,t)对每个方案在各指标下的满足程度进行评价,基于粗糙Choquet积分的PSS设计方案评价过程如下所示。
(1)确定PSS方案评价矩阵。k个专家采用{1,3,5,7,9}标度对m个方案相对于n个指标的满足程度进行评价,其中1,3,5,7,9分别表示“非常不满意”,“不满意”,“一般”,“满意”,“非常满意”。令表示第k个专家对第i个方案相对于第k个指标的评价值,则专家Ek的评价矩阵Ak=

(2)确定PSS方案粗糙评价矩阵。根据式(1)~式(6)将决策矩阵Ak中的确定数值转化为粗糙数形式,粗糙数反映了专家评价信息的不确定性。假设专家Ek的粗糙评价矩阵为=,根据式(8)和式(9),采用算术平均法集结专家评价信息,集结后的粗糙群决策矩
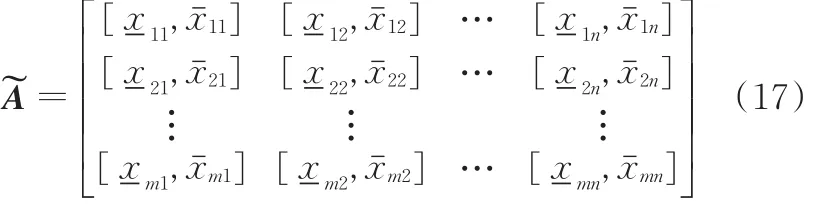

(4)将顾客需求重要度作为评价指标的模糊测度,根据式(13)确定参数λ的值。根据式(11)~式(12)计算评价指标各属性集A的λ⁃模糊测度,则∀A∈C,C={Ci|i=1,2,…,n},属性集A的λ⁃模糊测度计算公式如下:
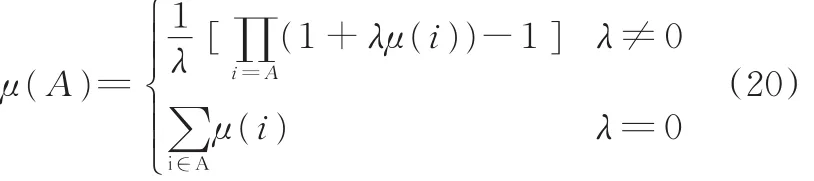
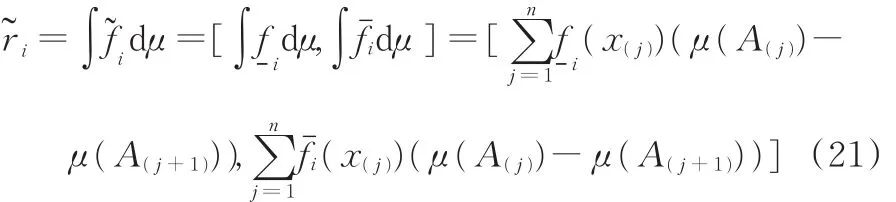
其中,下标(·)表示方案Pi在评价指标Cj下的粗糙评 价 值在属性集合A上的排序,且,且A(j+1)=0。
(6)依据各方案的集结结果~ri,根据式(7)和式(10)对方案进行排序,其中~ri值越大表明方案越优。
3 案例分析
3.1 某打印机PSS方案评价
某公司自成立以来始终秉持“共生”的企业理念,在美洲、欧洲、亚洲等区域均设立总部,形成了全球化与本土化有机结合的经营体制。该公司事业以光学技术为核心,涵盖了办公用品、影像系统产品以及产业设备等诸多领域。目前,该公司为推动其特色打印机的发展并进一步打入全球市场,提高产品竞争力以获得可持续发展,欲对其某特色商用打印机PSS研发过程中确定的多个可行性方案进行评价和选择,从而集中各方资源保证PSS方案的有效实施。经PSS方案多目标配置优化后共生成{P1,P2,P3,P4,P5}5个方案,5个备选方案属性规格描述见表1;专家小组共3位专家,其中包括产品设计工程师、市场营销工程师、客户研究工程师;根据设计初期确定的顾客需求项目,经专家组讨论后确定了6项主要顾客需求作为PSS方案评价的评价指标C={C1:打印清晰度,C2:打印速度,C3:噪声,C4:功能丰富性,C5:耐用性,C6:能耗},采用文献[21]中顾客需求重要度的确定方法计算其权重依次为:0.43,0.31,0.25,0.39,0.27,0.35。采用所提粗糙Choquet积分方法对5个方案进行评价,评价过程见表1。

表1 备选方案集属性规格Tab.1 Attribute specifications of alternatives
(1)确定PSS方案评价矩阵。3位专家采用{1,3,5,7,9}标度对各方案相对于每个指标的满足程度进行评价,评价结果见表2。
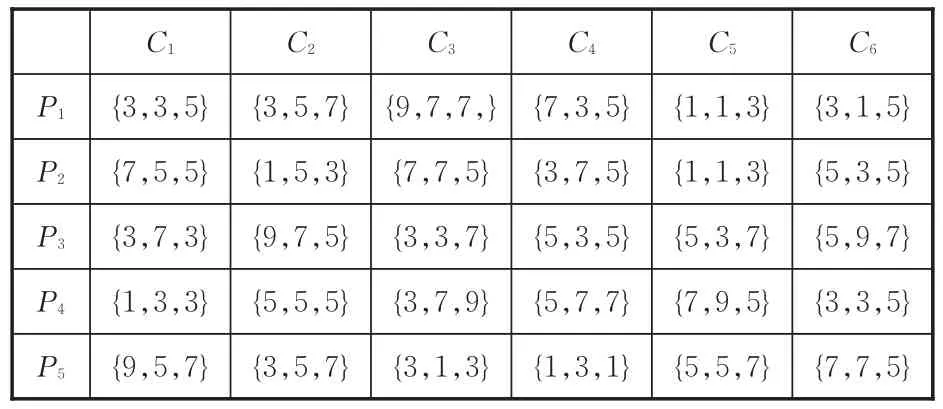
表2 备选方案的专家评价值Tab.2 Experts’evaluation values of alternatives
(2)确定PSS方案粗糙评价矩阵。以表2中方案P1相对于指标C1的评价值3为例,将表2中的专家评价值转化为粗糙数的过程如下:根据式(1)~式(6),计算数值3的下近似和上近似为
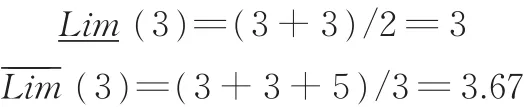
所以,粗糙数Rmm(3)=[3,3.67],同理,Rmm(5)=[5,5]。根据式(8)和式(9)采用算术平均法计算方案P1相对于指标C1的各专家的群决策值为
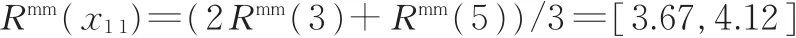
采用同样的方法得出PSS方案粗糙评价值见表3。
(3)粗糙群决策值规范化处理。根据式(18)和式(19)计算5个方案的归一化粗糙决策矩阵见表4。
(4)根据评价指标Ci(i=1,2,3,4,5,6)的重要度:0.43,0.31,0.25,0.39,0.27,0.35,采用式(13)计算得出λ=-0.87,根据式(20)计算各属性集的λ⁃模糊测度。以计算属性集C={C1,C2}的模糊测度为例,模糊测度

表3 备选方案的粗糙评价值Tab.3 Experts’rough evaluation values of alternatives

表4 备选方案的粗糙规范化矩阵Tab.4 Rough normalization matrix of alternatives
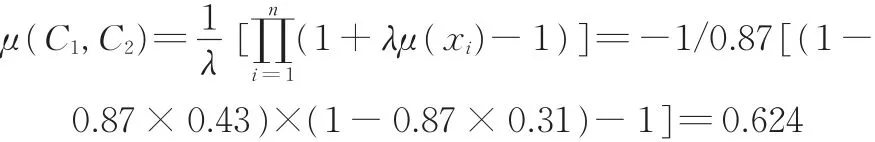
采用同样的方法可计算其他属性集的模糊测度见表5。
表5 属性集的模糊测度Tab.5 Fuzzy measures of attribute sets
(5)对各方案的粗糙评价值进行Choquet积分。以方案P1为例,根据式(7)计算表4中方案P1粗糙评价值的可能度矩阵P=[pij]6×6为

然后采用式(10)得出方案P1在指标C1下评价值的排序向量为
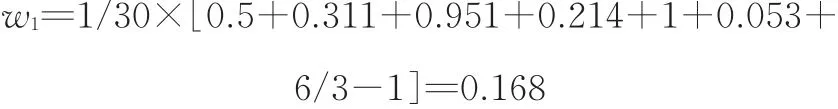
同理计算得出方案P1在其他指标下评价值的排序向量依次为:0.193,0.112,0.205,0.091,0.232,由此得


采用同样的方法,计算得出其他方案的Cho⁃quet积分结果分别为
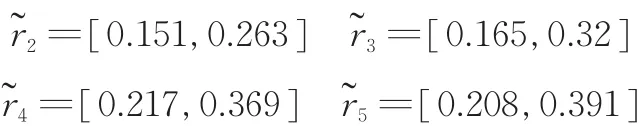
(6)方案排序。采用式(7)和式(10)计算各方案集结结果(i=1,2,…,5)的排序向量为:0.191,0.155,0.189,0.230,0.233。根据排序向量得出各方案的排序为
3.2 比较和分析
为对比所提方法的有效性,采用不同方法对方案进行评价。其中,M0表示所提方法得出的方案评价结果;M1表示采用传统Choquet积分对表2中的方案评价值进行集结得出的方案评价结果;M2表示采用粗糙TOPSIS得出的方案评价结果,M3表示采用ANP计算指标权重得出的方案评价结果,计算结果见图2。
由图2可知,4种方法的排序结果并不一致。为优选出满足顾客需求的PSS设计方案,所提方法以顾客需求作为评价指标进行PSS方案评价。考虑到顾客需求间的关联关系会对方案评价结果产生一定的影响,采用模糊测度表达指标间的相互关系;针对专家主观评价过程的模糊性,采用粗糙数处理方案评价信息;最后采用基于模糊测度的Choquet积分算子将指标间的交互关系反映到方案评价值的集结过程中,进行方案优选。
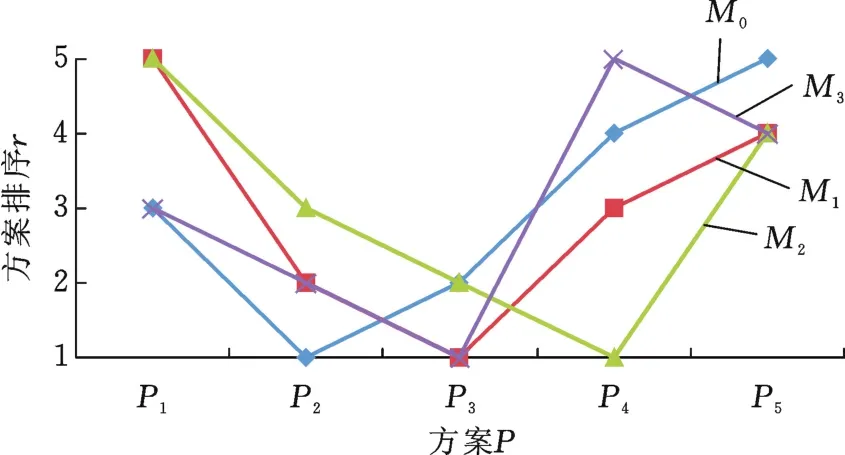
图2 4种方法评价结果对比Fig.2 Comparison of four methods’evaluation results
M0(所提方法)与M1(传统Choquet积分集成)相比,M0的排序结果是P2<P3<P1<P4<P5,M1的排序结果是P3<P2<P4<P5<P1。2种方法排序结果不一致的主要原因是所提方法考虑到了专家评价信息的模糊性和不确定性。例如,针对方案P1,3位专家在6个指标下的粗糙群决策值为:[3.67,4.12],[4.00,6.00],[7.22,8.11],[4.00,6.00],[1.22,2.11],[2.00,4.00],而算术平均法计算得出的专家群决策值为:3.67,5,7.67,5,1.67,3。传统Choquet积分方法通过算数平均法对专家评价信息进行集结,忽视了信息的模糊性,导致方案评价结果存在偏差。而所提方法通过粗糙数对评价信息进行处理,通过区间的下限、上限表达信息的不确定性,其决策结果更符合客观事实。
M0(所提方法)与 M2(粗糙 TOPSIS)相比,M2的排序结果是P4<P3<P2<P5<P1,这2种方法排序结果不一致的主要原因是M2忽视了评价指标间的关联关系。粗糙TOPSIS考虑到评价过程的模糊性和不确定性,通过比较各方案与理想方案的贴进度进行方案排序,而TOPSIS在定义决策问题的最优、劣解时未考虑到指标间的关联关系。实际决策过程中,评价指标间往往存在替代关系、互补关系等,这些关联关系的存在会在一定程度上影响评价结果的正确性。所提方法中Choquet积分算子通过λ⁃模糊测度反应指标间的相互关系,提高了方案评价结果的准确性。
M0(所提方法)与M3(ANP)相比,M3的排序结果是P3<P2<P1<P5<P4,与M0的排序结果也存在一定偏差。ANP在计算指标权重时也考虑到了指标间的相互影响关系,而在建立两两比较矩阵过程中需要专家进行多次评价,定性成分较多,容易产生不一致性现象,计算结果误差较大。Choquet积分算子不需要专家主观判断各指标间的关联关系,其λ⁃模糊测度是根据其初始重要度计算得出,定量计算的结果更为客观。
4 结语
(1)在评价信息的处理过程中,充分考虑了信息的不确定性和模糊性,采用粗糙集的方法将评价值转化为粗糙数形式,提高了决策结果的客观性和准确性。
(2)为优选出最大程度满足顾客需求的PSS设计方案,采用顾客需求作为方案评价指标。一方面顾客需求在设计初期已经获取,作为评价指标可减轻工作量;另一方面以顾客需求作为方案评价的依据与PSS的基本思想和最终目标相一致。
(3)考虑到各指标并不是相互独立的,通过模糊测度表达指标间复杂的相互关联关系,采用Choquet积分得出方案优选结果。不同于ANP法和DEMATEL法,Choquet积分通过分析指标间的关联关系并进一步确定指标权重。Choquet积分算子基于指标间的关联关系完成方案评价值的集结,更为直观地反映出指标间的关联关系对最终方案评价结果的影响。
(4)所提方法已应用于某企业打印机PSS设计方案的评价,通过实例验证了所提方法的可行性;同时,所提方法考虑到决策过程的不确定性和评价指标间的关联关系,有效提高了PSS设计方案评价的准确性。

