构造函数 曲径通幽
2018-11-08 02:34边红霞
数理化解题研究 2018年28期
边红霞
(河北省易县中学 074200)
函数是高中数学最重要的内容,一方面,函数性质的综合运用,使数学达到了一个无与伦比的境界,另一方面,函数思想渗透到数学的各个分支,如近几年高考导数试题,都以函数为背景,探讨方程、不等式、参数的取值范围等问题.在解答的过程中,当遇到阻碍,几经曲折,山穷水尽之处,构造函数,成为力挽狂澜之举.
一、确定方程的根
函数、方程、不等式三者之间存在着密切联系,经常通过相互转化来达到解决问题的目的.特别是对于求方程的根,一些复杂的多种运算构成的方程,更是无从求解,这时,可以考虑构造函数,利用函数的零点,来确定方程根的个数.
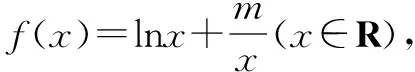
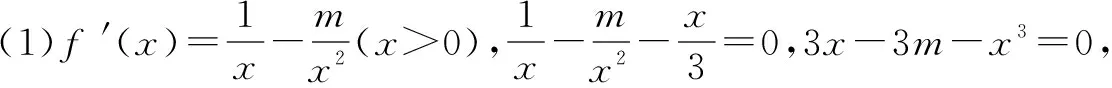
二、证明不等式
在证明不等式时,当所证式子的结构非常复杂,用通常的比较法、配方法、分解因式等方法不能正常解决时,可以构造函数,通过求导,利用函数的单调性、极值等生成不等关系,证明不等式,使解答过程峰回路转.
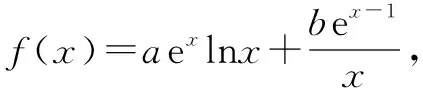
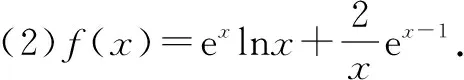
三、求参数的取值范围
对于求参数范围问题,一般是通过函数思想来解决.但为了解答的方便,当式子的结构复杂、思路不清晰时,往往要先进行变形,然后再构造新函数,通过研究函数的极值来解决.
例3 (2013年全国卷Ⅰ理)设函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2;(1)求a,b,c,d的值;(2)若x≥-2时,f(x)≤kg(x),求k的取值范围.
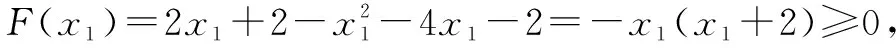
综上,k的取值范围是[1,e2].
在解答导数问题中,都以函数为前提,无论是方程、不等式、参数的范围,都是在适当的时候构造函数,利用函数思想解决,在遇到重重困难时,构造函数,曲径通幽!
猜你喜欢
新世纪智能(数学备考)(2021年10期)2021-12-21
小猕猴智力画刊(2021年11期)2021-11-28
中学生数理化(高中版.高二数学)(2021年4期)2021-07-20
河北理科教学研究(2020年3期)2021-01-04
河北理科教学研究(2020年1期)2020-07-24
中学数学杂志(2019年1期)2019-04-03
新高考·高二数学(2017年6期)2018-03-29
数学大世界·中旬刊(2017年3期)2017-05-14
广东技术师范大学学报(2016年5期)2016-08-22
高中生学习·高三版(2016年9期)2016-05-14

