基于Relief 算法与ReLU核ELM的煤矿开采最大下沉预测模型研究

魏 勇，唐延东，喻 强，杨春兰

(1.四川工程职业技术学院 建筑工程系，四川 德阳 618000；2.成都理工大学 地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059；3.西华大学 土木建筑与环境学院，四川 成都 610039)

煤矿开采地表最大下沉值是反映地表移动与变形程度的一个重要参数，水平移动和各项变形值的大小均可表示成最大下沉值的关系函数。针对煤矿开采下沉预测，国内外开展了大量的研究工作，并取得了丰硕的研究成果。

传统方法主要包括实测分析方法、影响函数方法及数值模拟方法等。Jung等人基于可靠量测数据，对地表沉陷的形成机理与预测方法进行分析研究[1]，该类方法能较好地处理演化规律较为简单的数据，若演化规律复杂时，则误差较大；Nicieza等人采用一种三维的n-k-g 影响函数预测地表下沉值[2]，该类方法在相似地质条件下十分适用，但是岩体地质条件往往复杂多变[3]；数值模拟方法有以阿威尔申为代表的连续介质学派和以波兰学者李特维尼申为代表的随机介质学派[4]，这两种方法均基于岩土结构情况、岩土力学参数及合理数学假设，需要取得大量且大范围区域的岩体物理力学及地质结构参数，这使得做到真实模拟的难度较高。其他研究方法(3S技术、灰色系统及神经网络等)也为解决该问题提供了相应途径[5-7]，但仍尚存诸多不足[8]。

随着非线性科学的飞速发展，一种名为极限学习机(Extreme Learning Machine，ELM)的单隐层前馈神经网络被广泛应用在各行各业[9-11]，该算法具有基本数学模型简洁、数据泛化能力强大、学习速度快及能够跳出局部最优解而获得全局最优解的优势。该算法也解决了传统神经网络选择隐函数层数的难题，便于应用及推广。

不同核函数往往适用于不同的数据类型，传统神经网络经常运用Sigmoid系方程作为模型核函数。该函数对中央区域信号增益大而对两头信号有抑制，从神经科学上看，中央区为神经元兴奋态而两侧为抑制态[12]。因此，该类核函数处理极值显著的预测问题会显得乏力。

随着神经科学的发展，科学家发现了生物神经具有稀疏激活性。Lennie[13]研究发现，人类大脑运作时，最多只有1% 的神经元被激活，而在传统神经网络运算时，其核函数有近乎一半的神经元被激活[14]，这一点不符合神经科学的研究，也不利于简化优化运算网络。大量研究表明[15-17]，因ReLU function 具有反对称结构，计算中不会出现两侧抑制的问题，函数图形状也较sigmoid更接近神经元的稀疏激活模式[18]。

另外，在解决非线性预测回归问题中，不同的输入参数往往得到不同的输出结果[19-21]，所以对输入参数进行筛选以获得最优输入数据就显得十分重要。作为一种特征权值算法，Relief Algorithm因其可根据各个参数与目标值的特征相关性，对参数赋予不同的权重值，而剔除权值小于阈值的参数，故可以做到筛选参数以优化输入数据[22]。

本文以阜新矿区36 个工作面的岩移数据为基础资料[23]，引入Relief Algorithm与以ReLU function为核函数的ELM算法，对煤矿开采最大下沉进行预测。首先运用Relief Algorithm对所获得的参数建立筛选优化模型，选出对最大下沉值贡献较大的参数而剔除贡献不是太大的参数。基于筛选优化后的参数，建立以ReLU function为核函数的ELM算法的煤矿开采最大下沉值预测模型；在预测模型中，对ELM的隐含层进行筛选以优化预测模型，且将该计算结果与ELM常用的核函数如Sigmoid function，Sine function，Hardlim function及Radial basis function的计算结果进行对比研究。

1 预测方法

1.1 Relief Algorithm筛选优化输入参数

Relief Algorithm是一种由Kira提出的特征权重算法[24]，算法根据参数特征对其他参数距离的区分能力计算参数的类别与参数间的特征。本文中，将所有岩移数据选出，作为m个样本，计算参数样本与目标样本在特征属性上的假设间隔。计算中，计算与目标样本距离最近的近邻样本(分为同类最近临点和不同类最近临点)，如果样本与同类最近临点距离小于与不同类最近临点，则认为该特征对区分样本是有益的，应该增加权值；反之，则是无益的，降低权值。以上过程重复P次，并累加作为特征权值。更新特征属性p的权值可用下式表达：

(1)

式中，x为参数样本；p∈P；H(x)为x的同类最近临点；M(x)为x的非同类最近临点。diff()函数形式见式(2)。

(2)

最后，得到各参数的特征权值。特征权值越大，表示该参数与目标关系越密切。根据所得的特征权值，以筛选预测模型输入参数。

1.2 基于ReLU function核的ELM预测最大下沉值

ELM是由南洋理工大学黄广斌教授提出用于求解单隐层神经网络的算法[25]。相较于传统神经网络，ELM在保障了训练精度的同时也兼顾了训练的效率。在训练初始，ELM随机初始化输入权重和偏置，并得到相应的输出权值；随着训练的进行，其权值随着训练样本及核函数进行相应调整。假设有N组样本(Xi，ti)，其中Xi=[xi1，xi2，…，xin]T∈RN,ti=[ti1，ti2，…,tin]T∈RM。即一个含有L个隐含神经元的训练网络可表示为：

(3)

式中，g(x)为核函数；oj为模型输出；Wi=[wi1，wi2，…，win]T为输入权值；βi为输出权值；bi为第i个隐含神经元的偏置。

训练的目的是使得输出的误差最小，即求解βi，Wi和bi，模型训练目标值tj值如式(4)可得。

(4)

式(4)用矩阵形式可表达为式(5)。

H=βT

(5)

式中，H为隐含层的输出；β为其输出权值；T为输出期望，其中：

H(a1,…,aL;b1,…,bL;x1,…,xN)=

β通过最小二乘法求解[26]：

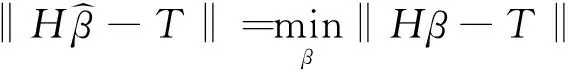
(6)

在隐含层输出列满秩时，利用Moore-Penrose广义逆进行求解，求解过程见文献[27]。

在本文所建立的最大下沉预测模型中，核函数选用ReLU function[28]：

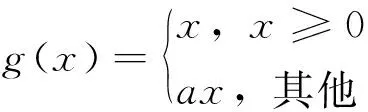
(7)

式中，a为小于1的常数，一般而言，a取值0.01。

ELM常用核函数Sigmoid function，Hardlim function及Radial basis function形式[29]如下：

Sigmoid function形式：

(8)

Hardlim function形式：

g(x)=2·hardlim(ai·x)

(9)

式中，定义hardlim(x)函数，当输入元素大于0时，函数返回1；否则返回0；ai为隐含层节点参数。

Radial basisfunction形式：

(10)

式中，σ为实常参数，且σ=1-accu，accu为算法信度，一般取值0.95。

2 案例分析

2.1 案例数据

搜集了阜新矿区36 个工作面的岩移数据[23]，分别有煤层采厚、煤层倾角、平均采深、走向长度、倾向长度、覆岩单向抗压强度以及对应的最大下沉，整理获得岩移数据，如表1所示。

2.2 优化参数结果

根据表1数据，建立最大下沉与6个参数特征类别判断的Relief 模型，并返回相应特征权值，计算结果见表2。

由表2 可知，在所有参数中，采厚与最大下沉的特征权值最大，达到了0.6650；而覆岩单向抗压强度、倾角与最大下沉特征权值最小，分别为0.0163和0.0096。由于特征权值的波动较大，数据间未能出现明显分层，也没有相应阈值可参考，不利于人工筛选参数。需要引入P-value检验对参数优化模型进行分析，从而筛选得到最优预测参数。

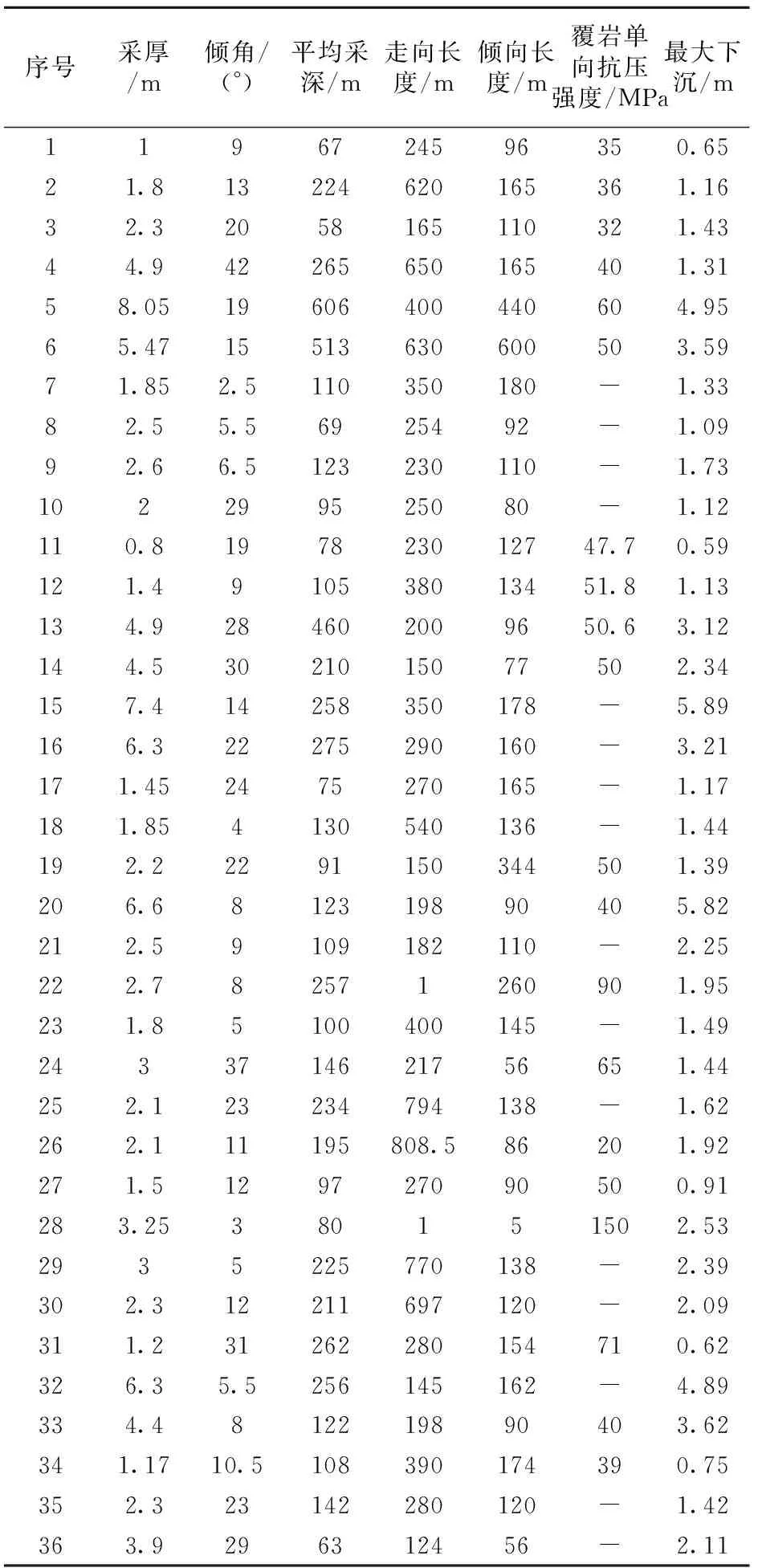
表1 岩移数据

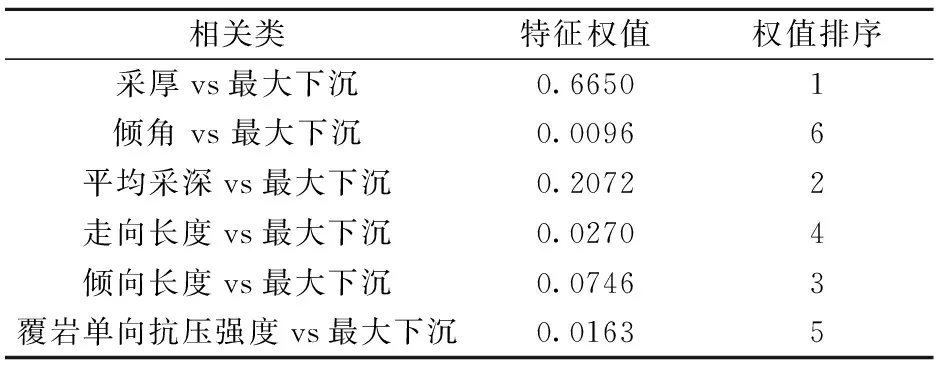
表2 Relief 模型计算结果

P-value检验是一项重要的推断统计内容，其计算结果为检验决策提供重要的依据。计算所得的P-value即是概率，在原来假设为真的前提下，对原假设的支持程度，反映其统计可靠差异性[30]。一般而言，以显著性水平0.05有统计学差异性。本文假设所有的参数均和最大下沉关系不显著，若P-value < 0.05，则计算结果拒绝了原假设；若P-value > 0.05，则计算结果接受了原假设；若P-value = 0.05，则需要增加样本重新计算。P-value检验计算方法及公式详见文献[30]，计算结果见表3。

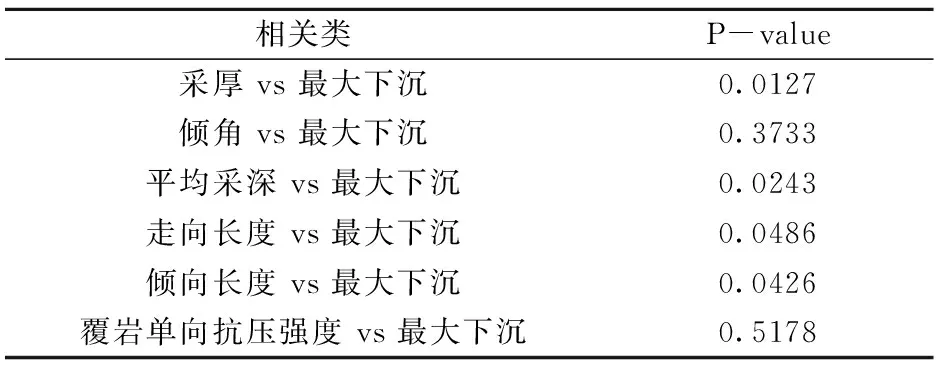
表3 显著性P-value检验计算结果

由表3可知，其中4组P-value<0.05，分别是采厚(P-value=0.0127)、平均采深(P-value=0.0243)、走向长度(P-value=0.0486)和倾向长度(P-value=0.0426)，说明采厚、平均采深、走向长度和倾向长度与最大下沉关系密切，可以作为预测模型的输入参数。而倾角和覆岩单向抗压强度的P-value均大于0.05。因此，在预测模型中将倾角和覆岩单向抗压强度两组参数剔除。

2.3 最大下沉预测结果

依据前文优化参数模型，建立以ReLU function为核函数的ELM最大下沉预测模型。模型中，选取前30组为训练样本，后6组为验证数据。以采厚、平均采深、走向长度和倾向长度为预测模型输入，最大下沉为预测模型目标。为了消除量纲及数量级的差异，所有数据均采用归一化处理。为了对比分析ReLU function核与ELM常用核函数Sigmoid function，Hardlim function及Radial basis function的差异，分别建立4类核函数的ELM预测模型，设置其隐含层数目为1组循环数，计算结果通过均方根误差(Root Mean Square Error，RMSE)评价精度。分别计算4类核函数的ELM预测精度，如图1所示。

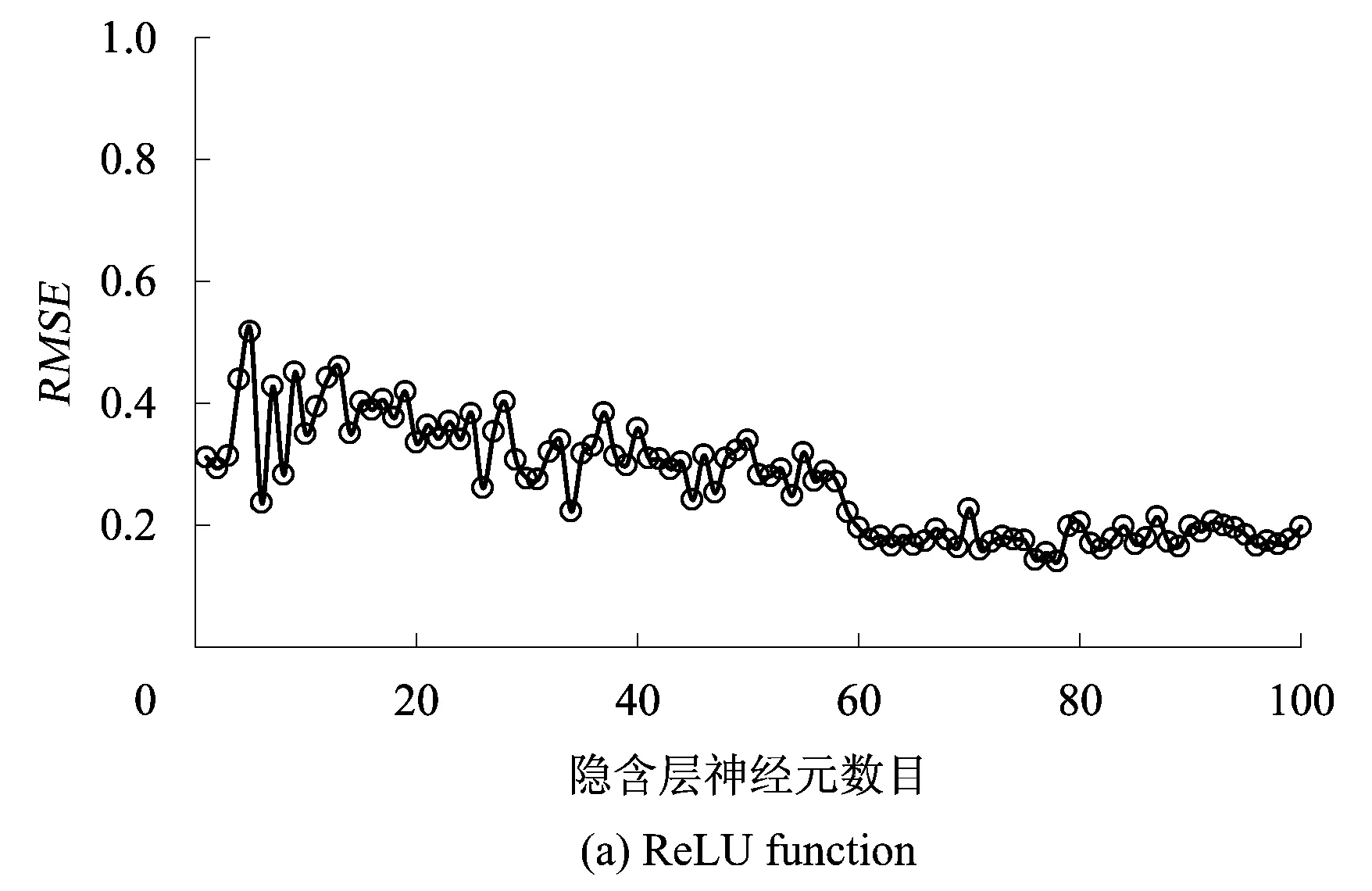
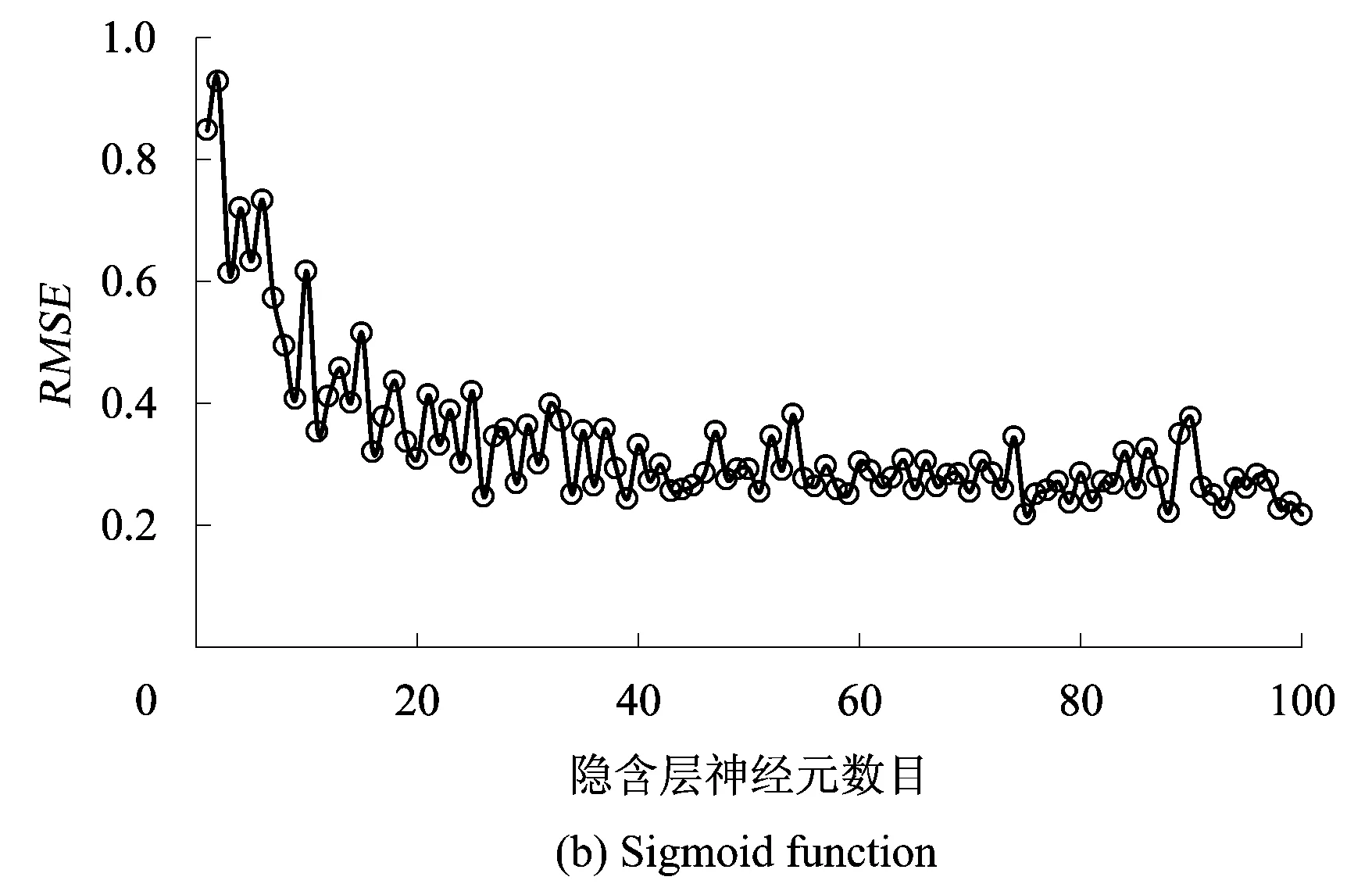
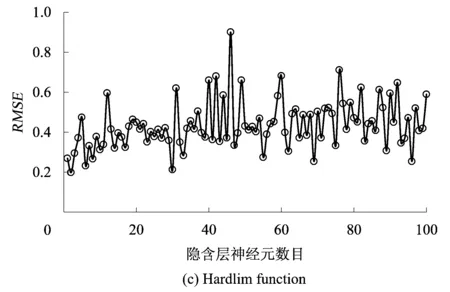
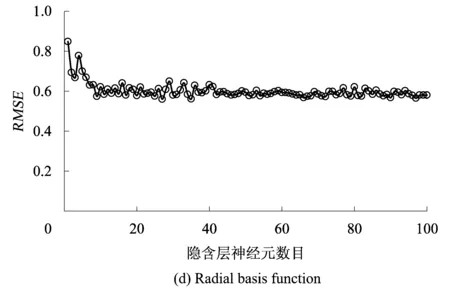
图1 不同核函数ELM预测精度

(11)

式中，N为样本数目；ti为最大下沉预测值；yi为原始最大下沉值。

由图1可知，ReLU function核、Sigmoid function核及Radial basis function的ELM返回的RMSE均随隐含层神经元数目增加有收敛的趋势，而Hardlim function核的ELM返回的RMSE无固定趋势，预测效果不好。就3种有收敛趋势的核函数而言，在隐含层神经元小于100时，Sigmoid function核能将RMSE收敛到0.2～0.4之间；Radial basis function核能将RMSE收敛到0.6；而在隐含层神经元数目达到57时，ReLU核能将RMSE收敛到0.2左右。据文献[31]可知，当RMSE达到0.2时，预测精度良好。因此，本文采用ReLU function核ELM最大下沉预测模型的隐含层神经元数目为57，其预测结果和原始数据如图2所示。

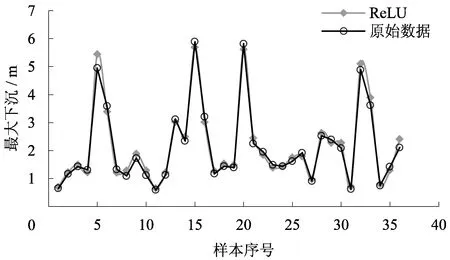
图2 ReLU核ELM预测结果

通过分析图2的预测结果可知，预测所得数据与原始数据的相关系数达到了0.9358，预测结果精度较高。

3 结 论

基于对核函数认识，本文首先引入Relief Algorithm对输入参数进行优化筛选，然后提出了将ReLU function的极限学习机算法运用到了煤矿开采最大下沉预测之中。主要结论如下：

(1)通过Relief Algorithm计算可知，采厚、平均采深、走向长度和倾向长度与最大下沉具有显著关系。因计算样本来自阜新矿区，煤层倾角和覆岩单向抗压强度差别不大，故在本例中煤层倾角和覆岩单向抗压强度与最大下沉关系不显著。

(2)通过隐含层神经元数目叠加实验可知，ReLU function核、Sigmoid function核及Radial basis function的ELM返回的RMSE有收敛的趋势，而以Hardlim function为核的ELM返回的RMSE无固定趋势，效果最差。其中，ReLU function核计算结果收敛趋势最优，精度最高。

(3)当隐含层神经元数目为57时，基于ReLU function核ELM的模型能获得计算精度较高的预测结果，其预测值与原始数据的相关系数达到了0.9358。