某型飞行模拟器荷兰滚模态的验证研究

赵善禄，闫思齐

(空军航空大学，吉林长春，130000)

0 引言

飞行模拟训练是提高飞行员操纵水平，进行风险科目训练，保证飞机飞行安全的重要手段。而在飞行模拟器的验证工作中，飞行品质是十分重要的一项验证内容，和飞行模拟器的逼真性息息相关。其中，荷兰滚模态的研究关乎横航向飞行品质，十分重要。

1 阻尼比及自振频率的验证

为了有效验证某型飞行模拟器的荷兰滚模态特性，对于阻尼比和自振频率的验证必不可少。另外，本文也选用了飞机荷兰滚模态中变化的六个重要参数来进行动态的定量验证，来增加验证的可信度。

在飞机荷兰滚模态中，阻尼比、自振频率参数是衡量该飞机模态特性的重要指标。因此，评价模拟器荷兰滚模态首先对比试飞数据与仿真模拟数据阻尼比和自振频率的一致性程度。

以5km高度条件下为例，该型飞机及其飞行模拟器荷兰滚模态阻尼比对比结果如图1所示，短周期自振频率对比结果如图2所示。

从图上可以看出，在高度5km条件下，试飞数据和模拟仿真数据荷兰滚阻尼比均大于2rad/s，满足国军标标准1的要求；自振频率则均大于0.1，满足国军标标准3的要求。

而为了进一步检验两者间的一致性程度，仍需通过具体的检验来确认。由于从图上难以确认两数据间的总体分布是否一致，这里采用秩和检验的方法来进行一致性检验，下面以阻尼比数据为例进行说明。

图1 5km高度下荷兰滚阻尼比对比图

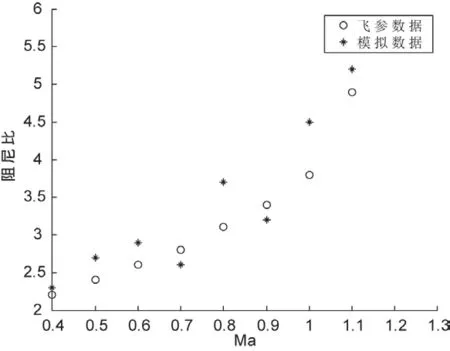
图2 5km高度下荷兰滚自振频率对比图

假设阻尼比试飞数据样本为X，仿真模拟数据样本为Y，将两个数据样本混合起来，按照从小到大的顺序进行排列，得到新的样本。两样本数据在新样本中的秩如下表1所示，

表1 阻尼比试飞及仿真模拟数据秩分析表

此时，n1=n2=9，n=18，

对于 α = 0 .05，查秩和临界表，可得，T1= 6 6，T2= 1 05。由于 T1＜R1＜T2，所以两组数据之间不存在明显的差异。

同理，计算可得，自振频率试飞数据及仿真模拟数据混合样本后，R1= 8 0.5。在 α = 0 .05时，满足 T1＜R1＜T2，两组数据间也不存在明显差异。

综上，在5km高度下，该型飞机及其飞行模拟器荷兰滚模态阻尼比、自振频率数据之间不存在明显差异，一致性程度较高。同理，经过验证，8km，11km，15km高度下该型飞行模拟器荷兰滚模态阻尼比、自振频率满足军标标准，且与真实飞机之间的一致性程度很高。

2 动态参数的验证

为了进一步检验该型模拟器荷兰滚模态的逼真程度，提取了与飞机荷兰滚模态过程中变化的四个参数来进行验证，分别是侧滑角、滚转速率、偏航速率和侧向过载。这里以高度5km，飞行速度0.4Ma条件下所测数据为例进行验证。

经过第三章数据预处理，所得试飞数据与仿真模拟数据对比结果如图3至图5.6所示，实线为试飞数据参数变化曲线，虚线为仿真模拟数据参数变化数据（其中仿真模拟数据为多次试验数据所取均值）。

图3 滚转速率时域响应曲线

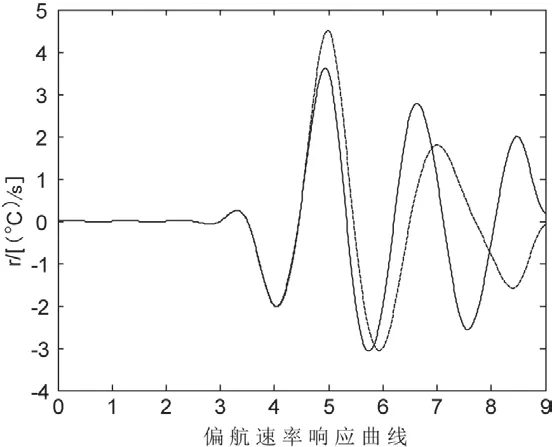
图4 偏航速率时域响应曲线

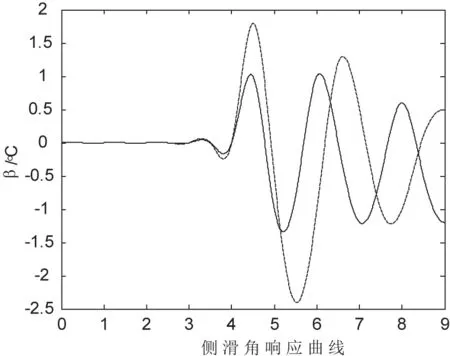
图5 侧滑角时域响应曲线

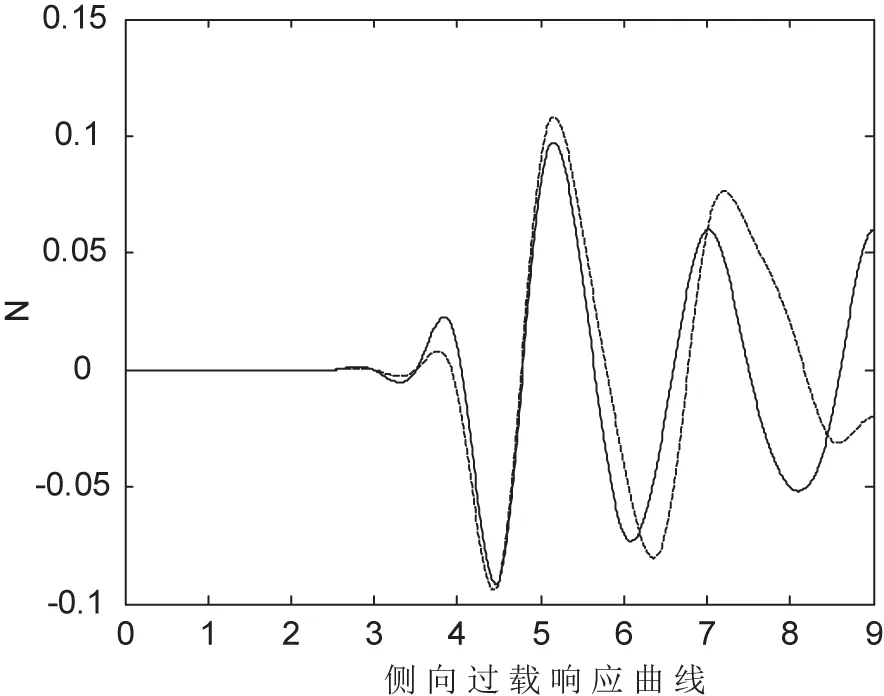
图6 侧向过载时域响应曲线

基于试飞数据和仿真模拟数据，仍然采用改进的证据理论融合时频域的方法来进行验证，这里以滚转速率数据为例来进行说明。在时域范围内运用平均标准化距离检验方法和灰色关联分析方法进行验证，在频域范围内运用经典谱估计方法进行验证，所得最终的基本概率分配表如下表2所示，

表2 证据体基本概率分配表

根据表2可知，各方法对于滚转速率的验证有一定出入，平均标准化距离检验方法和经典谱估计方法验证结果较好，而灰色关联分析方法效果则较差，因此需要进行结果的融合。如果根据经典DS规则直接对证据进行融合，则m(A)=m(B)=0，与客观判断不符，因此仍应根据本文改进的证据理论来进行证据融合。经过计算，最终可得，5km高度下滚转速率仿真结果动态一致性程度为0.71。

同理，可求得偏航速率等其它三个参数仿真模拟结果与试飞数据间的一致性程度，如下表3所示。

表3 荷兰滚相关参数一致性程度分析表

可知，在5km高度，0.4Ma下荷兰滚相关四个参数试飞数据和模拟仿真数据之间的一致性程度均大于0.65。

按照上文方法，计算5km，8km，11km，15km不同高度不同马赫数下所测得的试飞数据与模拟仿真数据之间的一致性，列于表4。

表4 不同高度不同马赫数下荷兰滚模态动态参数一致性程度表

从表上可以看出，在不同高度、不同马赫数条件下，荷兰滚模态四个参数试飞数据和仿真模拟数据的一致性程度在（0.65,0.9）之间。因此，该型飞行模拟器仿真数据序列与实际飞机试飞数据之间的一致性程度较高，该型飞行模拟器荷兰滚模态逼真度较好。

3 结论

本文提出了一种时域与频域相结合的仿真数据动态一致性检验方法，并对比阻尼比和自振频率，对某型飞行模拟器荷兰滚模态进行了验证。提取了该型模拟器荷兰滚模态四个相关参数的时间历程曲线并改进了证据理论，从而合成了时域和频域的一致性检验结果。最后，验证所得，该型飞行模拟器荷兰滚模态逼真度较好。