例析近似数中的 “精确度”

周艳峰

(江苏省泰兴市老叶初级中学 225400)

在现实生活中，近似数应用十分广泛.它常常根据不同的要求用四舍五入法取近似数.因此，只有理解了近似数中“精确度”的含义，才能正确、灵活地按要求取舍近似值.下面举例分析近似值取舍中的“精确度”的意义及应用.

一、理解“精确度”

例1 八(1)班的小明与小丽的身高都是1.6m，但小丽说他的身高比小明的高7cm.试问：小丽的说法有可能吗？

情境刚创设，部分学生哄堂大笑，有的摇头，表示不可能，有谁有不同意见？

同学们议论开了，一分钟、两分钟过去了，仍没有人举手.

1.6m是准确数，还是近似数？

齐声回答：近似数.

那么你理解近似数1.6m的含义吗？

有名的快嘴小王立刻站起来说：“1.6m中的十位数上的数字6是由百分位的数字经过四舍五入法得到的，即他们的身高不少于1. 55m，而小于1.65m.”

既然这样，小丽的说法你同意吗？

“同意”，但附和的人不多.

假如小明的身高为1.55m，而小丽的身高为1.64m，此时他的身高按精确度为0.1m的要求就都是1.6m了，但他们的实际身高就相差了9cm，所以小丽说他的身高比小明高7cm，这种情况是有可能的.

这个问题看似简单，但学生如若没有理解近似值的含义，就会出现错误的判断.

二、运用“精确度”

对于运用逼迫思想估算其大小学生应用得很少，大部分无所适从.

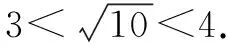
∵3.12=9.61<10, 3.22=10.24>10,

由于估计的近似值的误差要小于0.1

∵3.162=9.9856<10, 3.172=10.0489>10,

三、逆用“精确度”

例3 某个大学生参加军训，进行打靶训练，必须射击10次，在第6、7、8、9次射击中，分别得了9.0环、8.4环、8.1环、9.3环.他的前9次射击所得的平均环数高于前5次所得的平均数.如果他要使10次射击的平均环数超过8.8环，那么他在第10次射击至少要得多少环？(每次射击所得环数都精确到0.1环)

本题作为探究和创新题，让学生在双休日动动手，动动脑，结果在周一要求学生汇报时，只有两个学生能得到正确答案，却说不出理曲.那么主要障碍是什么呢？通过调查发现，少数学生没有认真审题，没有弄清题目意思，部分学生说无法求出第1、2、3、4、5射击的环数，大部分学生没有领悟题后括号中的要求而出现错误答案.

设在第1、2、…、9次中每次射击的环数分别为a1、a2、…、a9，第10次至少得a10环.

a6+a7+a8+a9

=9.0+8.4+8.1+9.3

=34.8

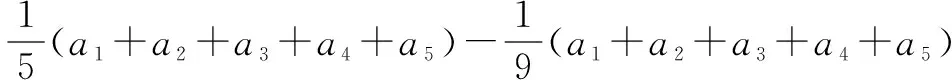
∴a1+a2+a3+a4+a5<43.5.

∵ 每次射击所得环数都精确到0.1环,

∴a1+a2+a3+a4+a5的最大值为43.4.

∴a10>9.8.

故这个大学生在第10次射击中至少要得9.9环.

本题解决问题的关键要通过观察、分析，领悟“精确度”的逆用思想.

由此可见，只有了解了“精确度”的含义，才能准确理解、运用、逆用“精确度”.