初中数学教学中数形结合思想的应用
陈宜建
(福建省三明市第三中学 365000)
一、在教学中培养学生数形结合的意识
数形结合思想在初中数学的运用中是非常广泛的,数形结合顾名思义是指将繁琐复杂的数字与直观立体的图形结合起来,并通过一定的转换,解决问题.我国数学家华罗庚说:“数形结合百般好,隔离分家万事非.”有了数形结合思想的帮助,对于解答初中数学问题有很大的帮助.老师帮助学生建立数形结合的思维方式,有利于学生更好地解决问题,认清数学的实质,有利于教学质量的提高.在初中教学中,培养学生建立数形结合思想意识是非常重要的.那么如何培养学生的数形结合思维,并将它们运用到实际问题中呢?
正所谓“兴趣是最好的老师”.要讨论如何在教学中教会学生运用数形结合思想去解决问题,首先要解决如何培养学生的数形结合思想,以及如何激发学生的兴趣.得益于当前社会经济与科学技术的发展,多媒体等电子教学设备已经走进了学生们的教学课堂中.运用多媒体设备,老师对学生进行数形结合思想的培养无疑会简单许多.例如初中数学中有一类计算两车相遇的问题,在讲解这类题目时,教师不妨先运用多媒体将两车相遇问题转换成两直线之间的距离问题,将题目更加简单明了地呈现出来,再引导学生运用数学方法得出答案.此外,在数学问题中,老师要引导学生多多实践,鼓励学生将数形结合思维运用到实际问题中.
二、数形结合思想在初中数学有理数中的应用
有理数章节在初中数学中是重点教学内容.有理数这一章节的学习是实数,代数式,不等式方程学习的基础,由于有理数是整数和分数的集合,教师在开展这一章节的学习时,可有效地利用数轴来表示任意有理数,同时这也是数形结合思想中典型的实例应用.例如,若a>0,b<0,且∣a∣>∣b∣,比较a,b,-a,-b之间的大小关系.这道题要比较他们之间的大小关系,就需要画出数轴来进行明确的表述,绝对值在这里指的是在数轴上这个数的点到原点的距离,画出数轴,从而得出这四者之间的大小关系.如果只是用具体的数如设a=4,b=-3,这种特殊值法虽可解出结果,但不免留下以偏概全的嫌疑.这种画数轴的方式,不仅简单易懂,还会使得解决问题的方法更具有全面性而且准确率大大提高.
三、数形结合思想在初中数学代数中的应用

四、数形结合思想在初中数学概率计算中的应用
概率是初中数学教学的重点内容之一,概率的学习与现实生活也有着极其紧密的联系.但因为这部分内容具有一定的抽象性,往往老师在教学过程中存在一定的讲解困难,学生在学习过程中也会产生理解上的困难.因此,针对于概率章节的教学,我们在教学过程中引入了数形结合的方法,将其运用到概率的学习中,可以使复杂的问题简单化,原本抽象的问题变得具体,从而轻松地解决问题.例如,概率中有部分几何概型的运算,就是典型的运用数形结合思想来解决问题.通过计算图形的面积,用图形的面积之比来表示最终结果.
五、数形结合思想在几何题中的应用
初中数学除了代数数字部分的运算外,另外一大块重点就在于几何问题的处理.有的学生空间思维能力不强,不能将几何图形有效地结合起来,导致这一块处理起来十分的复杂.对于这种情况,老师应在数学的教学过程中积极地鼓励学生,引导学生,多尝试着去用数形结合的方法去解决一些图形问题..
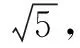
由上面例子可以看出,要灵活地运用数形结合的思想方法,由空间向数字,由数字向空间,相互转换,老师可在日常的教学活动中逐步地向学生渗透,让学生多多运用这种方法解决问题,使得学生逐步建立起知识体系,学会灵活地处理数学问题,建立起自己的数学思维.
随着新课改的不断深化,初中数学教学也在随之发生变化,传统的教学模式在逐渐被改变,取而代之的是教师利用现代化设备进行的更为多元化的教学模式.数学是一门以研究客观世界的数量与空间几何之间的关系的学科,它同时具有数字的逻辑性、严密性,和几何图形的直观性,因此,数学学科具有一定程度上的复杂性,数学学科的学习也有一定的困难性.而数形结合思想作为一种重要的数学学习手段,在学生学习数学的过程中具有连接数字和空间几何图形的作用,能够将复杂抽象的数据转化成直观易懂的几何图形,大大降低了学生学习数学的难度.

