基于数学核心素养下学生逻辑思维能力的培养策略
薛法林
南京市临江高级中学 江苏南京 210000
一、充分调动学生思维积极性
1.兴趣激发
著名数学家爱因斯坦有一句名言:“兴趣是最好的老师。”在新课导入时,可讲与新授课题有关的小故事或做小游戏等来创设情境,适当增加趣味成分,激发学生的学习兴趣,调动学生思维的积极性。如在引入课题《等比数列的前n项和》时,先讲了一个案例:“假设你有一笔资金用于投资,现有两种方案供你选择,这两种方案回报如下:方案一:每天回报100元;方案二:第一天回报2元,以后每天的回报比前一天翻一番。两种方案的期限都是30天,请问,你会选择哪一种方案?”同学们对此问题产生了好奇,觉得很有趣,马上动手列式得方案一为:30×100=3000元,方案二为:2+22+23+…+230,但对方案二的式子又不知怎样去运算,但这个问题又必须解决。学生急切需要知道求和方法和计算结果。于是人人都处于一种热切期盼、主动探索、积极思考的进取状态之中。
2.实验演示激发
数学的高度抽象是数学的重要特点。数学的内容是抽象的,它的方法往往也是抽象的,因此要使学生对抽象的数学有所认识、能够理解、应通过学生自己实地观察,亲身体验或试验归纳来对数学知识进行学习和研究的方法,是培养学生学习积极性、启发他们积极逻辑思维的好方法。
二、切实有效上好课,培养学生逻辑思维能力
1.上好数学概念课,讲清概念的内涵
数学概念是进行判断、推理和建立定理的基础,清晰的概念是正确逻辑思维的前提。讲解时,要特别重视数学概念的提出过程、建立过程、发展过程。如果抽象的给出定义,学生除了感到突然外,更重要的是不能对概念的内涵有真正的理解,也就失去了训练学生思维好的载体。
2.注重过程教学,提升学生的理性思维水平
概念的引入是为了建立定理(性质),为学生发现客观真理、认识客观真理做准备的。数学里定理的证明,大多是用分析法找出来的。因此,在平时数学教学中应自始至终强调分析的方法。证明定理时,除了要求一步紧跟一步,一步比一步更接近结论,还应在关键的地方多问几个“为什么”“怎样想来的”。这样做,既可以培养学生自我判断的能力,又可以加深学生对证明方法精神实质的理解。
三、教会学生正确的思维方法,提高思维品质
有了思维的积极性,掌握了思维的素材,那么怎样教给学生正确的思维方法,使学生的思维沿正确的方向前进呢?个人认为需要特别注意以下几点:
1.运用分析与综合方法,发展学生的逻辑思维
分析与综合是两种互逆的逻辑思维过程,前者是从结论推向前提,起点明确,方向清楚,每步有根有据,最易为学生掌握,是觅寻真理获得思路的重要方法。后者正好相反,是从前提推向结论,出发点较难选择,但却是书写表达的最好形式。如果把分析与综合统一起来,就能使学生的逻辑思维活动迅速发展。
2.在重视正向思维的前提下,学会进行逆向思维
怎样培养学生逆向思维能力呢?在数学教学中,经常进行以下几方面的训练,是非常重要的:原命题成立,想一想它的逆命题成不成立;从正面不易求解,看一看从反面下手行不行;从数式看不好解,试一试用图像是否会好一些;对于比较复杂的问题,还应从题设到结论、从结论到题设这种经过多次正反两个方向的思考来寻找解题途径。
3.教会学生判断自己的逻辑思维,发展自己的逻辑思维,提高逻辑思维水平
在进行思维活动时,如果学生能够对自己的思维活动的正确性加以判断、加以发展,那么,我们的教学就成功了一大半,要做到这点,除了要求学生对基本概念和基本定理有正确的理解和掌握外,还应教会学生在自己的思维活动中多问几个“为什么”、“根据什么”、“怎样想来的”,特别是经常问自己,题目还有没有别的解法,题目还能不能变化、引申,即进行“一题多变”和“一题多解”的思考,以培养学生举一反三,触类旁通的能力。如对解析几何题“过抛物线y2=2px的焦点F的一条直线和抛物线交于A、B两点,设这两点的纵坐标各为 yl、y2,求证:yly2=-p2”,此题还可以进一步变式:
(1)求弦AB的长的最小值;
(2)求△AOB面积的最小值;
(3)求弦AB中点的轨迹;
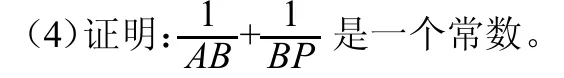
总之,学生逻辑思维能力的培养是一项长期、艰巨的任务。在平时的教学中,教师特别注重启发学生的思维,训练学生的思维,提高学生思维层次,使学生知识视野更加开阔,能力进一步增强,从而培养和发展学生的逻辑思维能力,提高学生的数学核心素养。

