X形钢阻尼器盆式支座设计与分析
王海龙,曹文静,唐斯聪
(河北建筑工程学院,河北 张家口 075000)
盆式支座因其竖向承载力大、水平滑动位移大、转动灵活、结构紧凑等优点在大中型连续梁桥中得到广泛应用。盆式支座在正常使用状态或小震作用下均能发挥较好的减震作用,然而在强震作用下支座的摩擦力不足以消耗强烈的地震力,导致滑动支座的上支座板剪断,桥墩与主梁之间出现较大的相对位移[1]。对于此问题出现了不同的改进意见。郭磊等[2]提出采用弹塑性减震耗能装置与其并联使用,以增加结构的附加刚度[3-4],减小支座的破坏程度,还能有效减小固定墩所受的地震力,改善结构的抗震性能。该理论的提出为桥梁的减隔震研究提供了新的思路。文献[5]提出了一种新型的减隔震支座——拉索减震支座,该支座是在普通盆式支座的基础上,结合国内普遍采用的一种限位弹性索装置而形成的,可充分发挥盆式支座及弹性索各自的抗震优点,并最大程度地克服了两者单独使用时的缺陷。
弹塑性钢阻尼支座和弹塑性钢阻尼器在国内铁路、公路桥梁都有应用案例[6-7]。这些应用案例为弹塑性钢阻尼元件在桥梁减震中的应用起到了良好的示范作用。目前应用在桥梁墩梁连接构件中的弹塑性钢阻尼元件有E形钢、C形钢和非线性阻尼等。其中E形钢阻尼力大,结构紧凑,安装方便,目前应用较多,但阻尼力的大小不好调整,设计起来比较复杂。X形钢阻尼器不仅结合了E形钢阻尼器的优点且在阻尼力大小的调整方面有了很大的改善,通过调整钢片数量就可调整阻尼力的大小。与E形钢阻尼器相比,X形钢阻尼器设计起来更方便,更容易推广,且钢材的利用率更高。
本文结合X形钢阻尼器的受力特点,将X形钢阻尼器与单向滑动盆式支座组合到一起,设计一种新型盆式支座。本文通过数值模拟及试验研究分析新型支座的滞回性能及工作特性。
1 新型支座的设计
新型支座的基本构造如图1所示。上连接板、X形钢片、下连接板构成整个X形钢阻尼器。上连接板与上支座板固结,下支座板、钢垫板及刚性挡块固结在一起。下连接板在支座高度方向不受约束,即下连接板与钢垫板之间有空隙,下连接板与刚性挡块固结,其作用为限制下连接板沿板长方向移动。
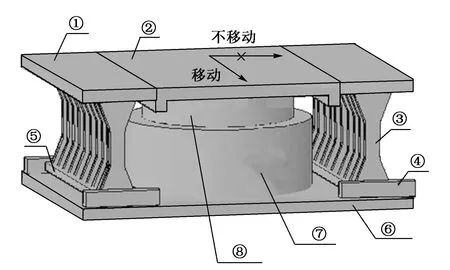
①上连接板; ②上支座板; ③X形钢片; ④刚性挡块; ⑤下连接板; ⑥钢垫板; ⑦下支座板; ⑧钢衬板图1 X形钢阻尼器盆式支座
2 材料选择及拉伸试验
金属阻尼器的耗能能力是通过金属的塑性变形来实现的。在阻尼器形状参数都相同的情况下,钢材的屈服强度决定阻尼器的阻尼力,其塑性决定阻尼器的疲劳寿命(低周疲劳性能)。因此应使用塑性好的软钢材料,但使用二级高强钢在满足同样阻尼力的情况下可以节约50%以上的材料成本[8-9]。文献[10]对使用Q345钢的ε形钢阻尼器进行疲劳试验,试验结果表明,Q345钢可以满足疲劳性能的要求。因此,本文中X形钢阻尼器使用的是Q345钢材。
为了测定Q345B钢材的基本力学性能,对其进行了金属拉伸试验,按照GB/T 228—2002《金属材料 室温拉伸试验方法》)和GB/T 2975—1998《钢及钢产品力学性能试验取样位置及试样制备》的要求制备试样。试验所得应力-应变曲线如图2所示。
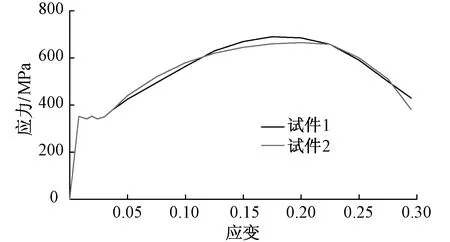
图2 应力-应变曲线
2个试件的截面面积均为217 mm2,根据图2得出钢材的力学性能,实测结果见表1。
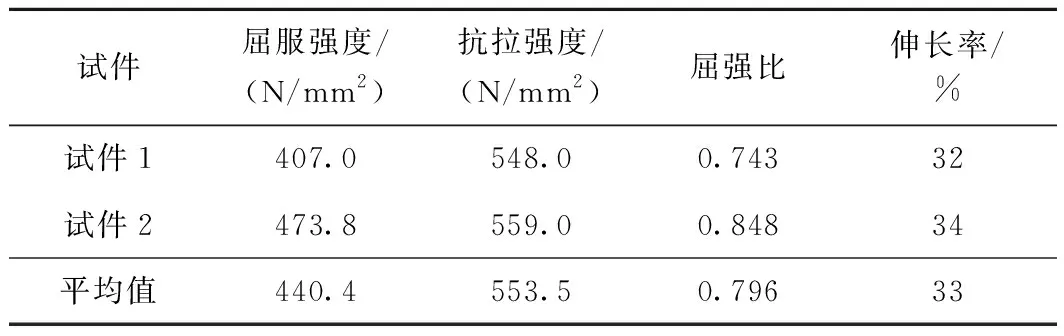
表1 钢材性能实测结果
3 数值模拟
3.1 模型的建立
由于模型是左右对称的,为了简化计算取支座的一半建模。滑动支座的相对位移几乎完全是由聚四氟乙烯板和不锈钢板的相对滑动完成的,因此,模型分析时只考虑不锈钢板与聚四氟乙烯板之间的滑动摩擦,其中聚四氟乙烯板的弹性模量为1.0 GPa,不锈钢板的弹性模量为210 GPa。不锈钢板与聚四氟乙烯板采用可变形的实体单元建模,不锈钢板与聚四氟乙烯板之间建立相互作用,切向行为采用罚函数的形式,法向行为的压力过盈采用硬接触。钢阻尼器的力学参数采用表1中的平均值。
3.2 模拟结果
新型支座的滞回曲线见图3,2组滞回曲线都非常饱满,且加载位移越大滞回曲线越饱满。这说明加载位移与新型支座的耗能效果有关,加载位移越大耗能效果越显著。从滞回曲线的形式中可以看出其骨架曲线符合三折线的本构关系,说明X形钢阻尼器已经发生了塑性变形,发挥了耗能作用。
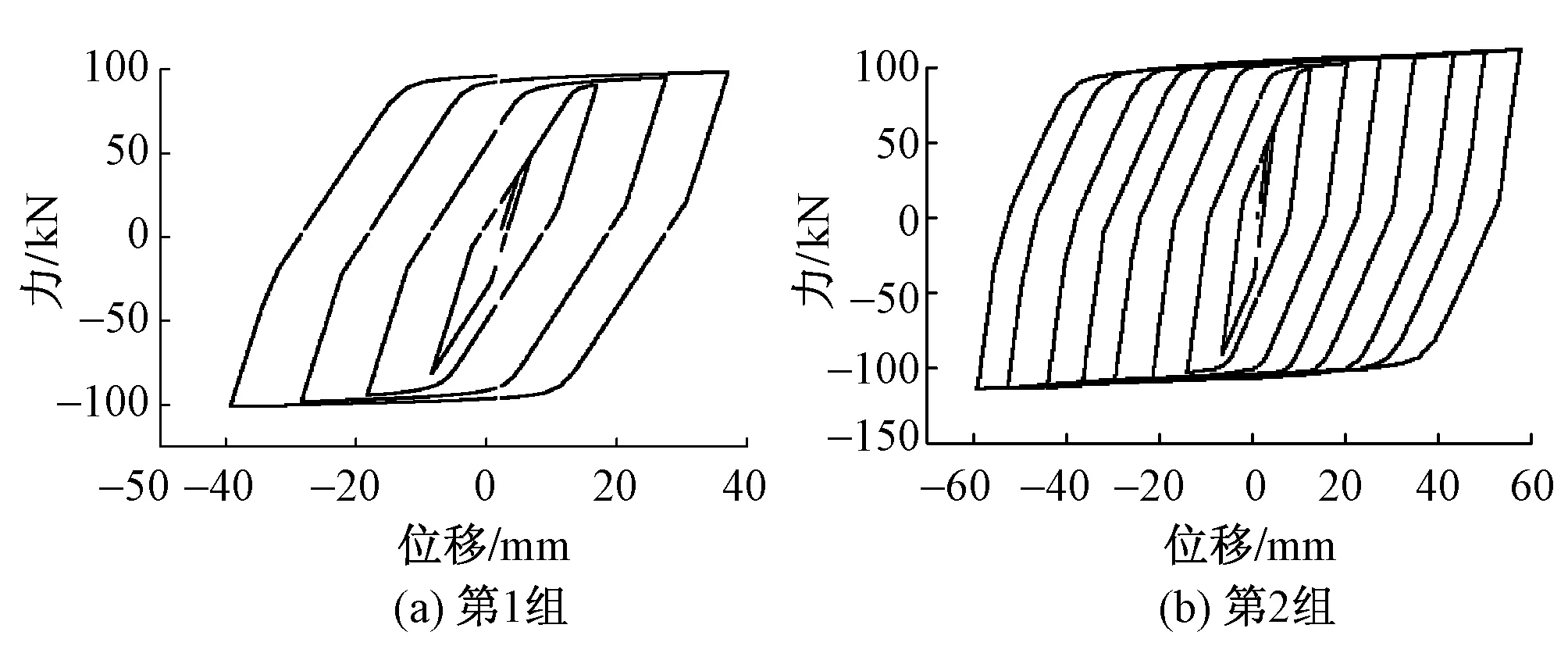
图3 数值模拟计算的新型支座滞回曲线
4 新型支座的拟静力试验
为了验证新型支座的力学性能,建立了新型支座的缩尺模型,并对其进行了拟静力试验研究。
试验时先将竖向荷载以连续均匀速度加载至30%设计承载力进行预压,保持10 min,再加载70%设计承载力,最终将竖向荷载加载到500 kN,整个试验过程中竖向荷载保持不变。水平加载采用位移控制,按正弦波循环加载,弹性阶段每级进行1次加载循环,塑性阶段每级进行3次加载循环。弹性阶段的加载位移幅值分别为±2,±4,±6,±8,±10 mm;塑性阶段的加载位移幅值分别为±15,±20,±25,±30,±35,±40,±45,±50,±55,±60 mm。平均速度为2 mm/s。
4.1 应变分析结果
试验过程中,在两侧的阻尼器A,B上分别布置了9个应变片,如图4所示。采用静态应变采集仪测量各点的应变。
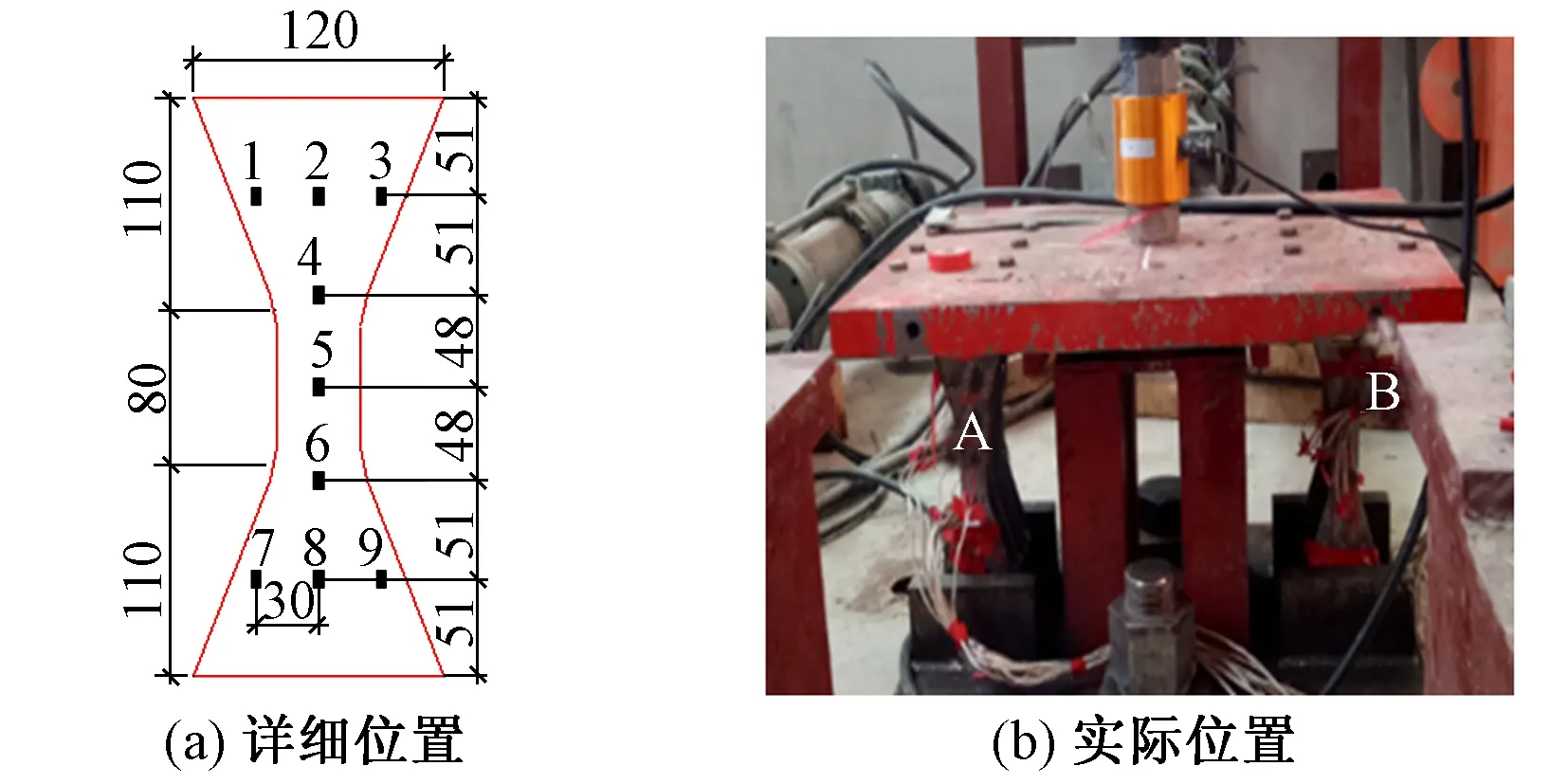
图4 应变片布置(单位:mm)
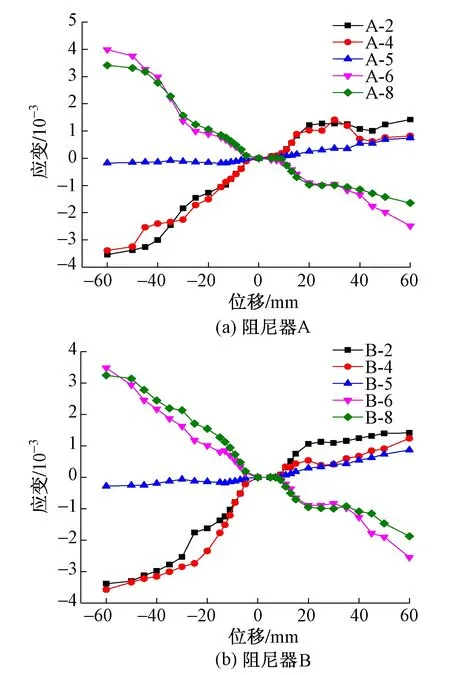
图5 应变-位移关系曲线
应变-位移关系曲线见图5,可以看出沿截面高度变化各测点的应变变化各不相同,其中测点5的应变值最小,测点2与测点4应变分布相同,测点6与测点8的应变分布相同;所测各点以测点5为中心对称分布,试验结果显示应变也是对称分布。负位移的应变值比正位移的应变值大,这是由于试验加载过程中支座的上支座板产生了倾斜所导致的。对整个X形钢片而言,沿高度范围内除中心点外各点的应变值几乎相同,说明该钢片的大部分区域都可同时达到屈服,材料可以充分利用。
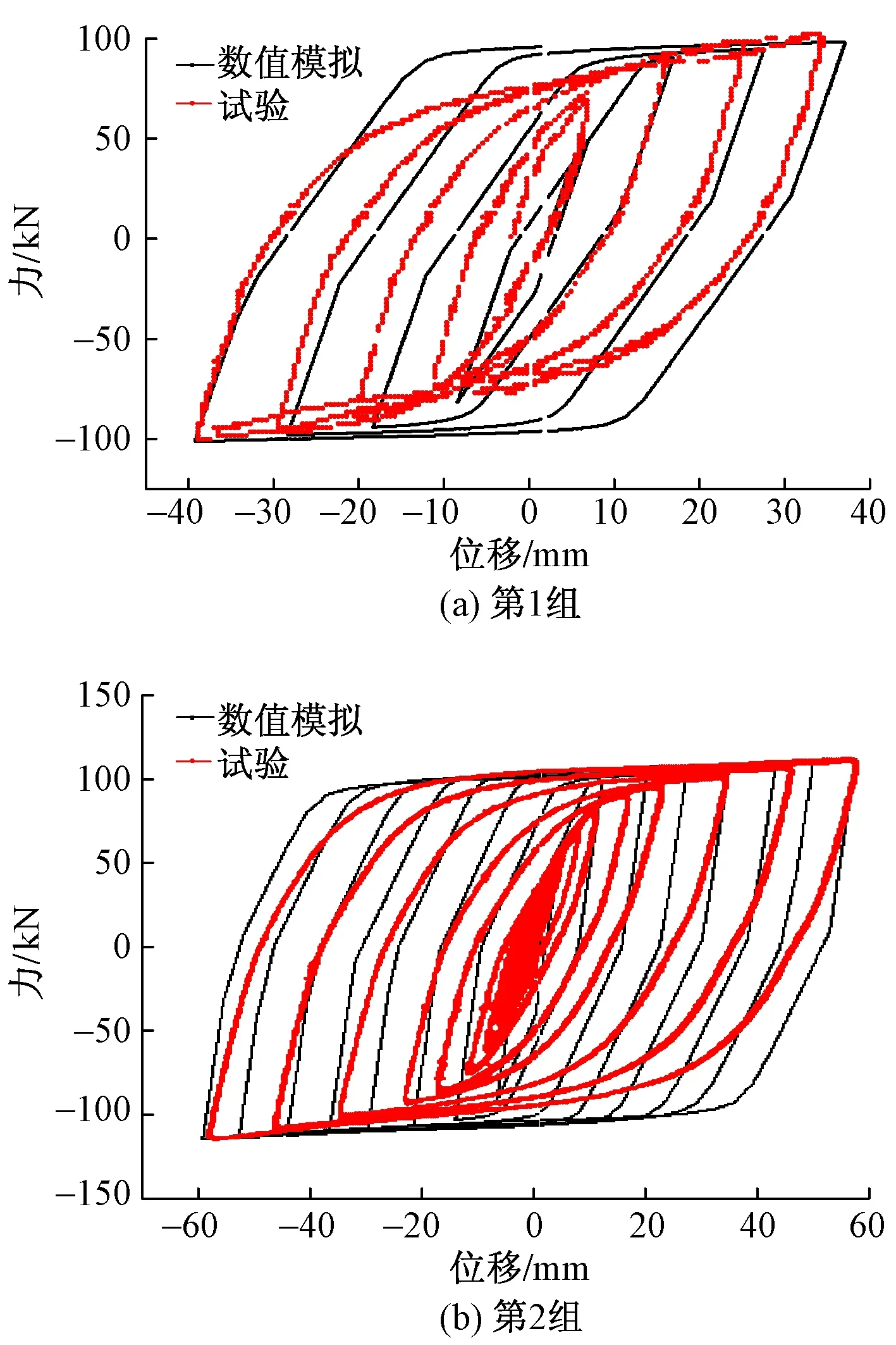
图6 滞回曲线对比
4.2 试验结果与数值模拟结果对比
为了验证有限元模型,将试验结果与数值模拟结果进行比较,所比较的最大加载位移分别为40,60 mm。
将试验所得滞回曲线与数值模拟所得滞回曲线进行对比,如图6所示。可以看出:①2组滞回曲线非常接近,当加载位移为60 mm时2条滞回曲线几乎重叠在一起。可见试验结果与数值模拟结果比较接近。②新 型支座的滞回曲线饱满,耗能效果好,且加载位移越大滞回曲线越饱满。在整个加载过程中没有出现荷载明显下降的趋势,说明新支座的工作性能比较稳定。
4.3 骨架曲线
从2组滞回曲线中可得到新型支座的骨架曲线,如图7所示。可以看出其骨架曲线接近三折线的形式,对应的有效刚度分别为第1刚度、第2刚度和第3刚度。当加载位移达到60 mm时,承载力仍未下降,说明该试件有良好的变形能力且力学性能稳定。
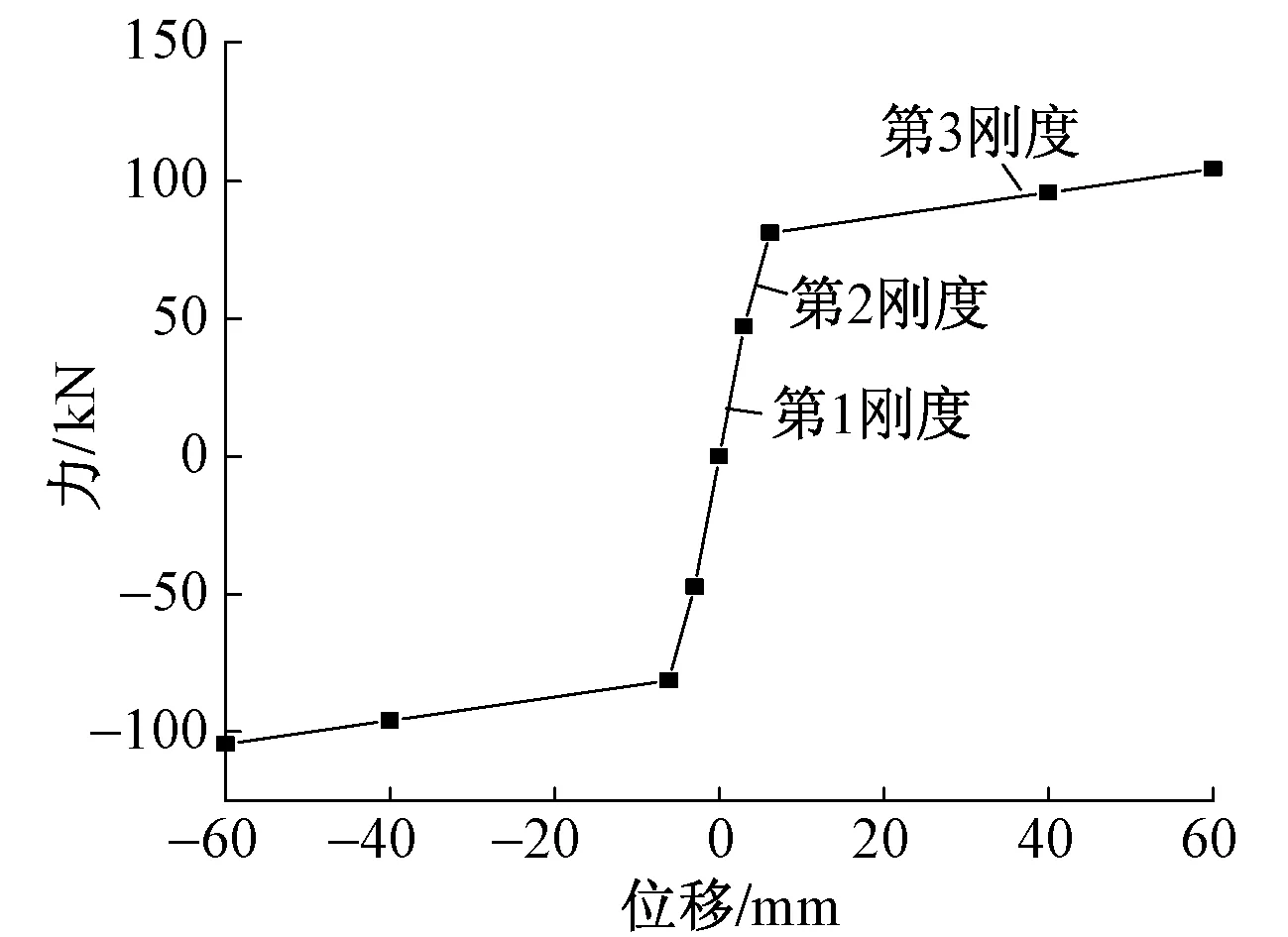
图7 新型支座骨架曲线
4.4 力学性能分析
对新型支座的力学性能参数通过数值模拟及试验研究相结合的方式进行了对比分析,其结果见表2。可以看出:试验结果略小于数值模拟结果,主要是因为试件制作的误差使得阻尼器与刚性挡块之间存在微小的缝隙,使得新支座的屈服位移增加,进而导致各个刚度均有所降低。

表2 新型支座力学性能参数对比 kN/mm
由表2可知,试验结果与数值模拟结果相当吻合,说明所建的有限元模型是合理的,试验结果是正确的。
5 结论
1)新型支座试验滞回曲线饱满,无捏拢现象产生,主要性能指标没有下降,新型支座的工作状态稳定。试验所得滞回曲线与数值模拟所得滞回曲线的对比表明,加载位移越大滞回曲线的吻合度越好。
2)新型支座的骨架曲线符合三折线的本构关系,且力学性能稳定,有良好的变形能力。
3)从X形钢片的应变分布来看,沿截面高度范围内除中心点外各点的应变基本相同,截面的大部分区域可同时达到屈服,钢材得到了充分利用。

