基于摄动法电力系统暂态稳定计算研究

，，，，，

(广西大学 电气工程学院,广西壮族自治区 南宁 530004)

1 引言

暂态稳定性分析计算是电力系统三大经典计算质疑，它是电力系统规划、设计、调度运行与控制必不可少的一项重要的计算任务。在正常的稳态运行情况下，各发电机输出的电磁转矩与原动机输入的机械转矩之间相互平衡，因而所有发电机的转子速度能一直维持恒定。但是，电力系统中不可避免地受到一些大扰动的冲击，例如，各类短路故障、大容量机组或大负荷的投入和切除等。电力系统的暂态稳定性分析，其主要目的是在大扰动的冲击时，各发电机维持同步运行的能力。

电力系统暂态稳定分析方法可以分为：时域仿真法、直接法、人工智能法、动态安全域方法。把以上方法当中的一种或者几种方法相互结合形成的混合法等。近年来，有关时域仿真算法许多的改进算法，主要目的是加快仿真速度或者提高计算精度。在数学上，暂态稳定时域仿真[1-2]可以表述为微分代数方程的初值问题。有联立求解和交替求解这两类方法。交替求解法是指微分方程组和代数方程组两者的求解彼此是独立但需要交替进行的。但会造成“交接误差”。由于显式数值积分方法的数值稳定性不太好，所以显式分离求解法的整体数值稳定性也不是很好。因此显式分离求解法在商业化的电力系统暂态稳定性计算程序中应用很少。联立求解法的基本过程为，先用隐式梯形积分公式把微分方程组进行差分化，它和代数方程组一起形成联立非线性方程组，然后求解此非线性方程组。所以，仿真算法的研究可以分为两种，一种是常微分数值积分方法，另一种是对非线性方程组的求解方法。常微分数值积分方法有改进欧拉法、隐式积分法、龙格-库塔法等，在此基础上也有改进方法。文献[3-5]研究了在电力系统中，中长期的暂态稳定性分析以及变步长变阶方法。文献[6]研究了不诚实牛顿法和变步长技术相结合的方法，提高了系统的仿真速度，验证算法的正确性和实用性。非线性方程组的求解方法一般用牛顿法迭代求解。文献[7]基于奇异摄动法，提出求解发电机状态变量和网络的节点电压的方法，计算量比牛顿迭代法要小，从而提高仿真速度。文献[8]通过引入新的状态变量，网络代数方程的形式发生了改变，计算过程中没有迭代和三角分解，大幅度的提高了计算速度。

本文应用摄动法进行电力系统暂态计算仿真研究。结合IEEE9及节点系统，从发电机的转速、机端电压、和仿真时间三个方面。验证该方法的有效性和实用性。

2 暂态稳定仿真的奇异摄动法

进行电力系统动态研究时，发电机和电力系统输电网络通常可以表达为：

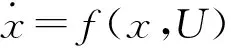
(1)

0=g(x,U)

(2)

式中：x是同步发电机的状态变量;U是网络的电压向量。

采用隐式积分的方法求解微分方程时，一般先把微分方程换成一系列代数方程，再用求解代数方程的办法求出时段终值。隐式梯形积分法的差分方程可以表达为：

(3)

因此，描述电力系统的动态方程(1)、(2)可以改写为：

xk+1=xk+εf(xk,Uk)+εf(xk+1,Uk+1)

(4)

0=g(x,U)

(5)

式中：ε=h/2，h为步长。

为简单起见，式(3)、(4)可写为：

x=B+εf(x,U)

(6)

0=g(x,U)

(7)

其中，设x=xk+1,U=Uk+1，B=xk+εf(xk,Uk)很显然在式(4)中ε是一个很小的常数，可以应用奇异摄动原理进行电力系统仿真计算，把x和U分别展开为ε的幂级数，令

(8)

(9)

ε0:x0=B

(10)

0=g(x0,U0)

(11)

ε1:x1=f(x0,U0)

(12)

(13)

(14)

(15)

式中：xx1，xU1和UU1都是向量，每一个元素均可由向量x1,U1解出。

因此，x0,U0可由(10)、(11)中求出，x1,U1可由(12)、(13)求出，x2,U2可由(14)、(15)求出。最后x和U可以表达为：

x≈x0+εx1+ε2x2

(16)

U≈U0+εU1+ε2U2

(17)

在计算中如果保留的次幂越高,精度也就会越高，但计算就会随之增大。实际计算表明，在一般的电力系统仿真计算中，保留前三项就能够满足精度要求。如果是在精度要求高时，则需要以保留更多的项来满足精度要求。

针对x0=xk+εf(xk,Uk)，x1=f(xk,Uk)，则可以得出：x0=xk+εx1

x=x0+εx1+ε2x2+o(ε3)=xk+2εx1+o(ε3)

(18)

U=U0+εU1+ε2U2+o(ε3)=Uk+2εU1+o(ε3)

(19)

综上可以得出：

ε0:x0=B,0=g(x0,U0)

(20)

(21)

从而可以得出：

x=xk+2εx1,U=Uk+2εU1

(22)

因此，若想求解x、U，只需求解出x0、U0和x1、U1，进一步减少了计算量。

3 电力系统暂态计算的数学模型

在电力系统暂态稳定计算中，当选用的元件的数学模型不同，所得出的计算结果会受直接影响，稳定性分析计算的复杂程度也会有很大的影响。因此，选择合适的数学模型来表示元件本身，不仅计算过程简单还可以得出满足精度要求结果。数学模型是电力系统暂态计算中的一个重要的问题。在工程实际问题中，根据使用场合的不同对发电机的模型做不同程度的简化处理。本文选用发电机三阶模型，负荷为恒定阻抗模型。

3.1 发电机三阶实用模型

在实际电力系统，暂态计算仿真分析中，当要计及励磁系统的作用时，能选择的最简单的模型就是三阶模型。它较适用于凸极机。这种实用模型基于如下假定：

(1)不考虑定子d绕组、q绕组的暂态；

(2)在定子电压方程中，设在速度变化不大的过渡过程中，其引起的误差很小；

(3)忽略D绕组、Q绕组，通过补入阻尼项到转子运动方程中来近似处理。

(23)

3.2 电力网络数学模型

电力系统暂态计算和潮流、短路计算中一样，用相量把电力网络的节点电压方程可表示成：

YV=I

(24)

式中：分别为电力网络的节点电流和节点电压组成的列向量；Y表示节点导纳矩阵。上式所描述的网络方程在形式上为线性方程组，其中的导纳矩阵Y仅由电力网络的结构和参数所决定。

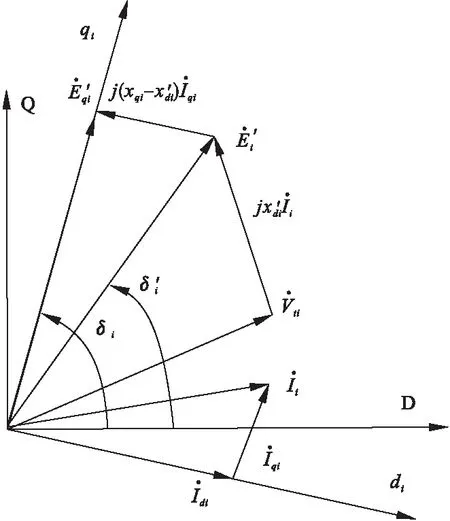
图1 第i台发电机的向量图

在电力系统中，为了求解电力网络方程，需要首先列写出每一个动态元件的本身的代数方程，并对其进行处理，从而才能和网络方程联立求解。

3.3 发电机与网络的连接

对于三阶同步发电机模型，在d-q坐标系下，定子电压方程都可统一表示为：

(25)

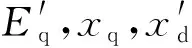
4 算例分析

本文的采用电科院3机9节点测试系统。仿真时间为5 s，设定故障为7号节点，0.1 s时发生三相短路故障，步长为0.001 s时，0.15 s时切出故障。

4.1 仿真精度对比分析

如图2所示，表示利用牛顿法求解时，1、2号发电机电压仿真曲线。图3表示利用摄动法求解时，1、2号发电机电压仿真曲线。

由图2、3可以看出，用两种方法进行仿真时，摄动法和牛顿法的计算结果曲线基本相同。所以，从这个意义上来说，验证了它们的精度是相同的。

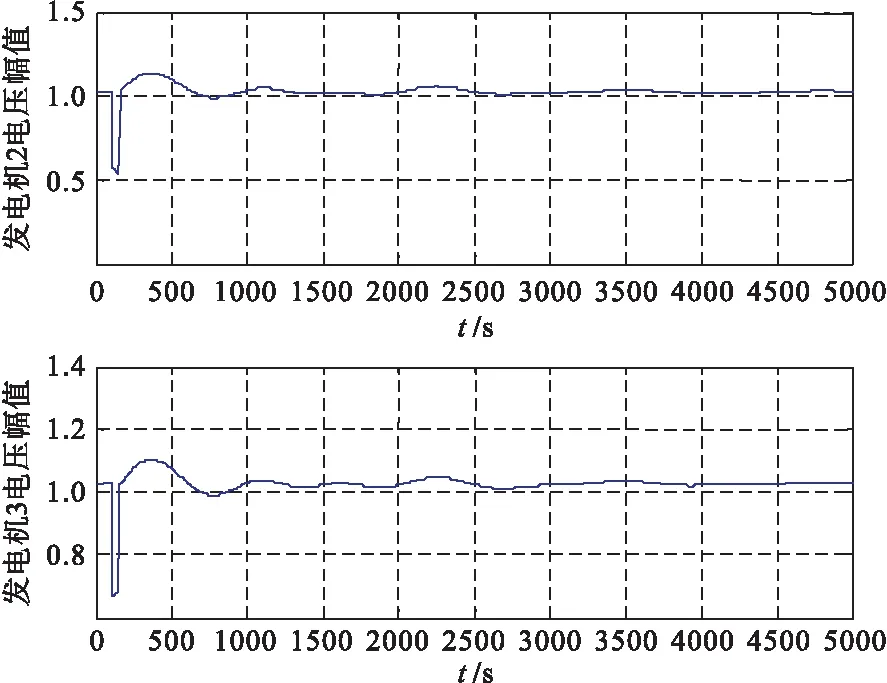
图2 牛顿法求解时，1、2号发电机电压仿真曲线

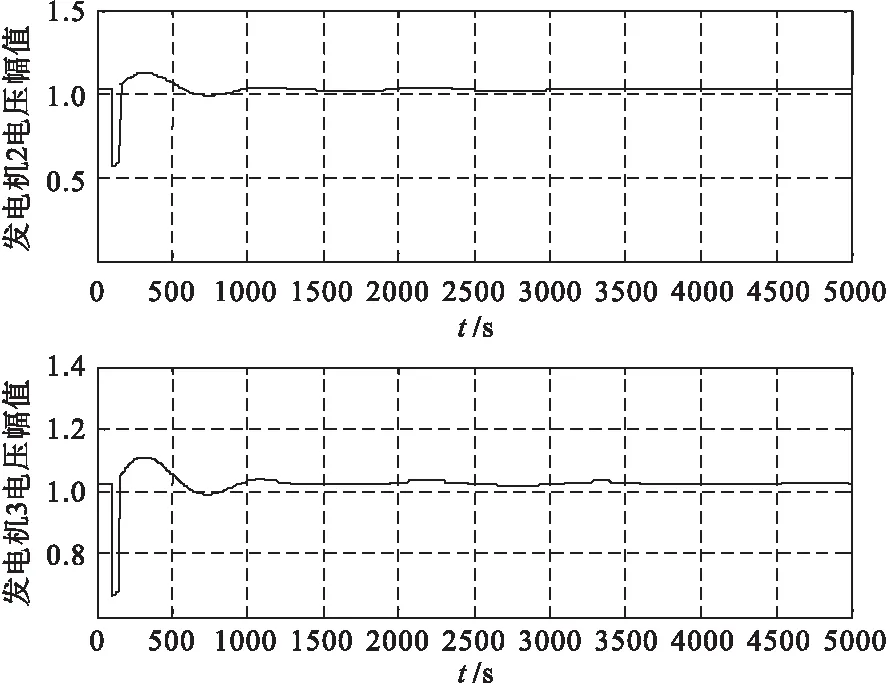
图3 摄动法求解时，1、2号发电机电压仿真曲线

表1 不同算法的仿真时间对比

4.2 仿真时间对比分析

由表1可以看出，当系统总仿真时间都为5s，牛顿法计算时间是0.462s，摄动法为0.075s，计算速度提高6倍。证明了摄动法的优越性。

5 结论

本文利用摄动法进行电力系统暂态计算，其计算速度比牛顿法要快，通过仿真，利用算例验证该方法在保持计算精度的情况下，而提高计算速度，取得较好的计算效果。