回转干馏炉内颗粒运动及停留时间分析

张立栋，韦庆文，李伟伟，张 轩，王 擎

(1.东北电力大学 能源与动力工程学院，吉林 吉林 132012；2.华能巢湖发电有限责任公司，安徽 巢湖 238015；3.榆林职业技术学院神木校区，陕西 榆林 719300)

油页岩是石油的补充能源，在石油对外依赖度较高的当今，油页岩的开发利用具有重要意义，其综合利用可以在一定程度上缓解我国石油资源供应不足的现状[1～2].通过不同的干馏方式，将页岩油从母岩中提取出来，是油页岩的主要利用方式[3～4].其中采用回转式干馏炉对油页岩进行干馏效率较高，且对物料的粒径要求较低，因此具有较好的应用前景.采用固体热载体的干馏方式，是通过固体热载体和油页岩之间传热将油页岩加热至理想温度450 ℃～600 ℃，之后油页岩发生热解[5].但由于颗粒在干馏炉内的运动过程较为复杂，采用实验的方法来研究颗粒在干馏炉内的运动较为困难，为更好研究干馏炉内的颗粒运动状态，采用数值方法模拟了页岩灰和油页岩颗粒在出口加装挡料板并且内置直角抄板的回转干馏炉内的运动过程.

诸多研究表明，对颗粒在回转窑内的停留时间等研究具有工程实际意义[6～8]，对于此方面的研究也逐渐被重视，如采用回转干馏装置干馏城市固体垃圾[9～10]、热解木炭[11]、炭素[12～13]等.Abouzeid[14]等采用轴向扩散的理论论证了回转窑内物料停留时间近似服从正态分布的规律.曲航等[15]通过研究得到了回转窑转速较小、筒体直径或填充度较大时，物料颗粒停留时间将增加的规律.顾丛汇等[16]研究了滚筒转速和倾角对滚筒内烟丝颗粒停留时间的影响.王恭等[17]以油页岩固体热载体干馏试验系统为数值模拟对象，在物料填充率和干馏炉转速固定的条件下，分析了颗粒在不同倾角下的停留时间.乔斌等[18]对回转窑内物料的停留时间进行了研究，得出了随着转速的增大物料停留时间减少的规律.Njeng等[19]采用实验的方法，研究了回转窑转速、物料的质量流率、回转窑的倾角对颗粒在回转窑内停留时间的影响.Ngako等[20]通过建立数学模型，研究了回转窑床层刨面深度和颗粒的速度分布与颗粒停留时间之间的关系.

以上研究更多的是对回转装置参数对颗粒停留时间影响的研究，较少涉及到对颗粒停留时间的分布规律进行检验.鉴于此，本文以回转干馏炉为研究对象，采用离散单元法(Discrete Element Method，DEM)模拟了颗粒在带抄板结构的三维回转干馏炉内的运动过程.先对示踪颗粒在运动过程中的集中分散特性进行了分析，之后不仅考察了转速对干馏炉内示踪颗粒停留时间的影响，还对不同转速下示踪颗粒停留时间分布的正态性进行了检验，并分析了转速对停留时间数据与正态分布拟合程度的影响.最后通过概率密度曲线来估计总体颗粒的停留时间分布.因此，为回转干馏炉运行条件及结构参数的优化设计提供有益的参考.

1 离散元模型的建立

1.1 接触模型

离散单元法最早由Cundall和Strack提出[21]，主要用于研究非连续性颗粒物质的结构和运动规律.硬球模型和软球模型是目前常用的处理球形颗粒接触理论的两类简化模型[22].硬球模型不考虑颗粒之间接触力的大小和颗粒表面的变形，碰撞属于瞬态过程，碰撞后速度的改变是碰撞过程中力对时间积分的结果.硬球模型适用于快速、低浓度颗粒流.软球模型同样忽略颗粒表面变形，但是考虑颗粒之间的接触力.软球模型将颗粒间的法向力简化为弹簧和阻尼器，将切向力简化为弹簧、阻尼器和滑动器.软球模型依据颗粒间的法向重叠量和切向位移计算接触力.软球模型适用于密集颗粒流.干馏炉中混合的油页岩和页岩灰颗粒属于密集颗粒流，在本文中颗粒间的接触模型采用软球模型.采用Hertz-Mindlin(No Slip)模型计算颗粒间接触力.法向力基于Hertz接触理论，切向力基于Mindlin-Deresiewicz理论[23].

法向接触力为

Fn=-Knδ+Cnνn，

(1)

切向接触力为

Ft=min(μFn，Ktδt+Ctνt)，

(2)

式中：Kn为法向刚度；δ为法向重叠量；Cn为法向阻尼系数；vn为法向相对速度；μ为滑动摩擦系数；Kt为切向刚度；δt为接触点的切向位移；Ct为切向阻尼系数；vt为切向相对速度.

1.2 颗粒运动模型

可将颗粒的运动分解为平动和转动[24].根据牛顿第二定律可得颗粒运动方程：

平动方程

∑fi=midνi/dt，

(3)

转动方程

∑Ti=Iidω/dt，

(4)

式中：∑fi为颗粒i受到的合外力；mi为颗粒i的质量；vi为颗粒i的速度；∑Ti为颗粒i受到的合力矩；Ii为颗粒i的转动惯量；ω为颗粒i的角速度.

1.3 模型的建立

1.3.1 建立几何模型

采用Gambit软件绘制回转干馏炉三维几何模型，并将该模型导入到离散元软件EDEM中.干馏炉的材料为钢材，干馏炉、油页岩颗粒、页岩灰颗粒的泊松比、剪切模量、密度参考前期的研究成果[25].回转干馏炉及颗粒参数，如表1所示.

表1 离散元参数

1.3.2 模拟对象参数及仿真过程

(1)干馏炉结构参数及操作参数：干馏炉内径d=84 mm，干馏炉长l=84 mm，出入口直径d′=d″=33 mm.内构件采用直角抄板，其中直板段a=17 mm，弯板段b=5 mm，直板段与弯板段夹角为90°，抄板厚度c=1 mm，6个抄板在干馏炉内均匀分布.干馏炉轴线与水平线倾角为3.24°(入口高于出口).干馏炉的主视图，如图1 (a)所示；剖面图A-A，如图1 (b)所示.物料填充率为1/3，油页岩颗粒直径为3 mm，页岩灰颗粒直径为1 mm，干馏炉中油页岩和页岩灰颗粒的整体质量比为1∶1.选取17 r/min、13.3 r/min、10 r/min、6.8 r/min、3.4 r/min五种转速进行对比.颗粒-颗粒及颗粒-壁面的恢复系数为0.1，静摩擦系数为0.9，滚动摩擦系数为0.01.

(2)仿真过程：颗粒产生时间0 s～0.5 s，页岩灰颗粒产生时间0 s～0.1 s，油页岩颗粒产生时间0.1 s～0.3 s，0.3 s～0.5 s颗粒处于静止状态，干馏炉从0.5 s开始旋转，仿真时间为100 s.从干馏炉入口处选取16个油页岩颗粒作为研究对象(示踪颗粒).油页岩颗粒从入口运动到出口的时间间隔，即为其在回转干馏炉内的停留时间.

图1 干馏炉结构图

2 颗粒运动分析

2.1 颗粒运动规律

以13.3 r/min为例，对颗粒在干馏炉内的运动进行分析.不同时刻下，示踪颗粒在回转干馏炉内运动情况，如图2所示.从图2中可以看出，分别在20 s、40 s、60 s、80 s、100 s，可以将示踪颗粒的运动过程分成两个阶段.第一阶段为颗粒集中阶段，第二阶段为颗粒分散阶段.在初始时刻，示踪颗粒在入口位置与其他颗粒初步接触.之后随着干馏炉的转动示踪颗粒开始和其他颗粒产生混合作用，虽然混合行为不断进行，但是示踪颗粒之间的距离仍然很小，示踪颗粒以颗粒群的形式出现，仅有少数颗粒与主体颗粒群的距离较远，整体上示踪颗粒较为集中，这一阶段称为集中阶段.在集中阶段存在少数示踪颗粒的分离现象，此时的分离以半径方向上的分离为主，称为径向分离，径向分离主要是由干馏炉的转动造成的.随着干馏炉的运行，示踪颗粒的运动进入分散阶段，在这一阶段，整体示踪颗粒群消失，示踪颗粒的分布较为分散，示踪颗粒不仅在径向上较为分散，在轴向上也较为分散，示踪颗粒在轴向上的分离称为轴向分离.因为干馏炉轴线与水平线存在一定的角度(本文中角度为3.24°)，干馏炉入口高度比出口高度高，随着干馏炉的运行，示踪颗粒不断从入口向出口运动，在运动过程中示踪颗粒的轴向移动有快有慢，因此产生了轴向分离.

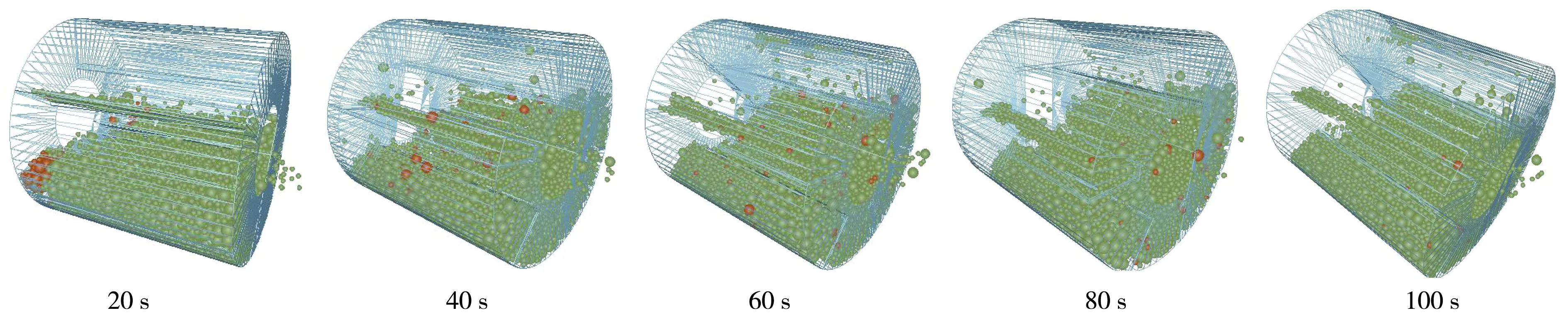
图2 转速为13.3 r/min时颗粒运动过程

在所选的时刻中，20 s处于颗粒集中阶段，40 s、60 s、80 s、100 s处于颗粒分散阶段.在20 s时示踪颗粒仍大多集中在入口处，随着回转干馏炉的转动入口区域的示踪颗粒逐渐减少.在40 s时，示踪颗粒主要分布在干馏炉中部靠近入口位置，但颗粒之间已经拉开了距离，颗粒不再集中分布.在60 s时示踪颗粒在干馏炉内的分布更加分散，颗粒之间的距离进一步拉大.当回转干馏炉经过一定时间的转动，示踪颗粒逐渐接近干馏炉出口(80 s)，此时已经有示踪颗粒流出干馏炉出口.之后不断有示踪颗粒从干馏炉出口流出.到100 s时，干馏炉内仅存在很少的示踪颗粒.随着时间推移，示踪颗粒将会全部从回转干馏炉内流出.因此，可以通过分析示踪颗粒的运动来推断全部颗粒在干馏炉内的运动.

2.2 停留时间分析

提取各工况下示踪颗粒在回转干馏炉内的停留时间，并计算平均停留时间(Mean Residence Time，MRT)及停留时间方差σ2，经整理后的数据，如表2所示.

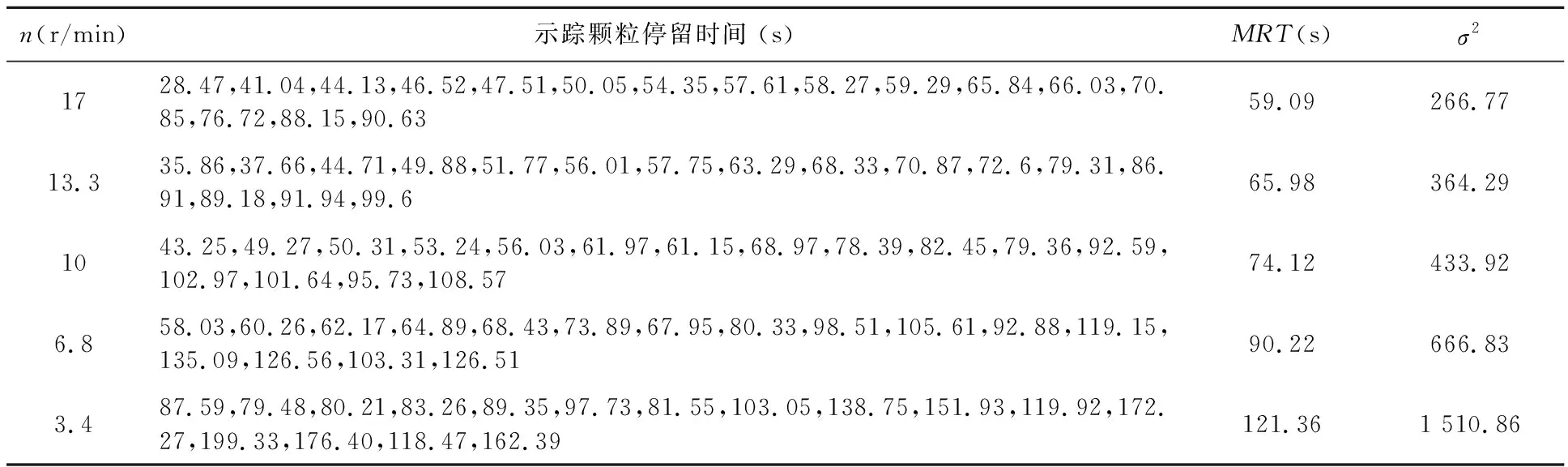
表2 示踪颗粒停留时间

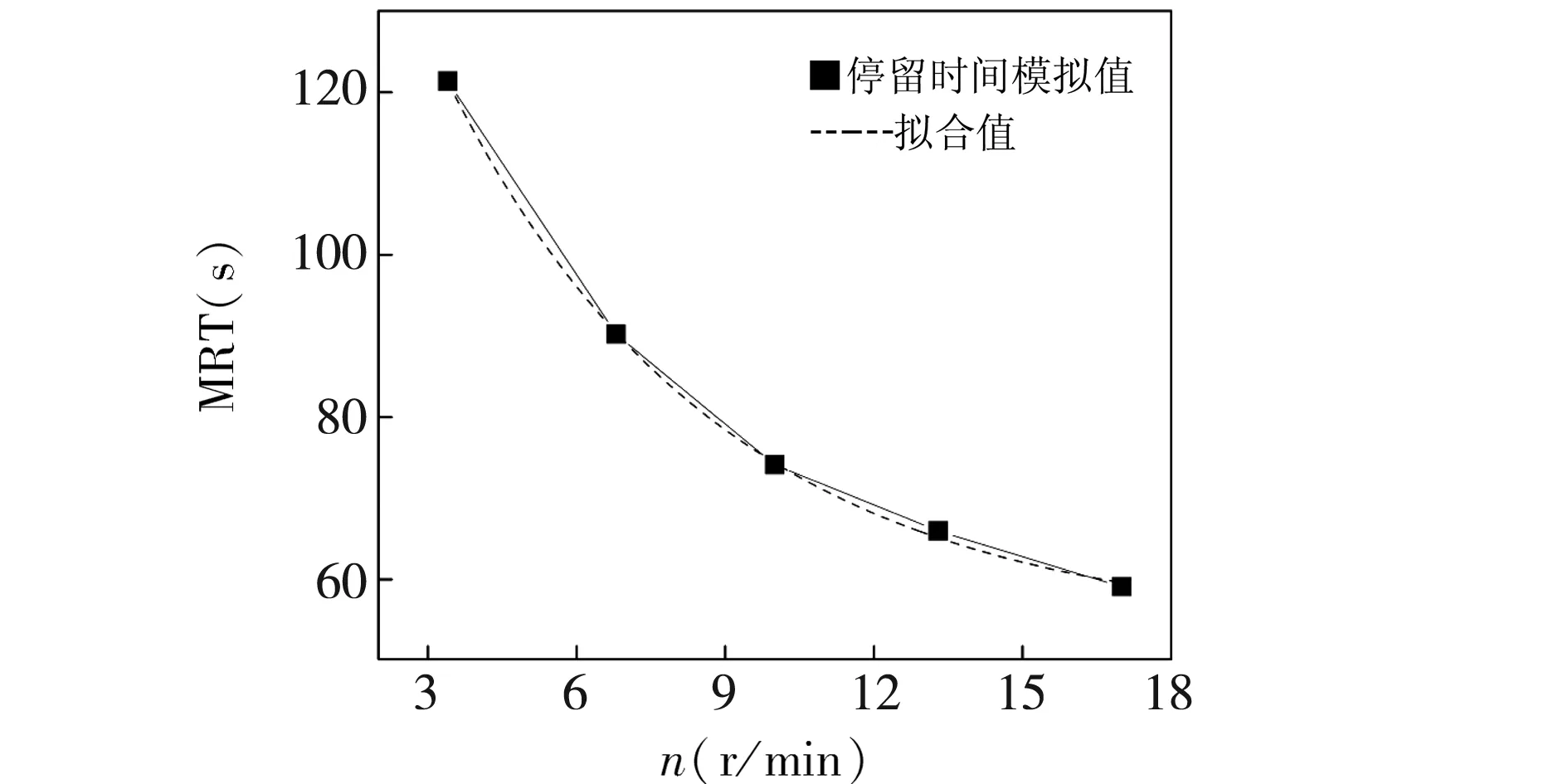
图3 转速与平均停留时间关系

从表2可看出,平均停留时间由小到大的顺序是转速17 r/min、13.3 r/min、10 r/min、6.8 r/min、3.4 r/min，说明平均停留时间随转速的减小而增大，但随着转速的增加，停留时间的减少逐渐放缓.

采用指数函数拟合转速与停留时间的关系，得到公式(5)，R2为仿真曲线和拟合曲线的相关系数，R2为0到1之间的数，R2值越大，表明相关性越好.本文中R2=0.999，相关性非常好.

MRT=a×exp(-n/t1)+b，

(5)

式中：a、t1、b为系数，其中a值为124.44；t1值为5.57；b值为53.71.

干馏炉转速与示踪颗粒在干馏炉内的平均停留时间之间的关系，如图3所示.带方块的实线为数值模拟得到的曲线，虚线为拟合曲线.示踪颗粒在干馏炉中平均停留时间随着转速的提高而逐渐减少，数值模拟得到的结果与文献[26]中的实验结果吻合较好.

通过参考文献[27]的实验研究可知，颗粒在回转干馏炉内的停留时间服从正态分布.因此，这里对数值模拟结果中的颗粒停留时间进行正态性检验.由于在干馏炉中选取的示踪颗粒数量较少，为小样本，因此采用夏皮罗-威尔克(Shapiro-Wilk)法[28]对示踪颗粒在干馏炉内的停留时间进行正态性检验.用夏皮罗-威尔克法检验所需要的统计量为

.

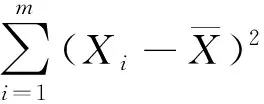
(6)

计算出一组数据的W，当W>W(m，p)时，则接受这组数据为正态分布.对于K值，当m为偶数时，K为1～m/2，当m为奇数时，K为1～(m-1)/2.在本文中m=16，所以K为1～8.将同一工况下所得到的停留时间数据值按从小到大的顺序排列，分别对应X1，X2，X3……X16.ak可通过查表获得.当m=16时，a1=0.505 6，a2=0.329 0，a3=0.252 1，a4=0.193 9，a5=0.144 7，a6=0.100 5，a7=0.059 3，a8=0.019 6.当置信概率为0.95，通过查表可得：W(16，0.95)=0.887.

分别计算出各工况下的W值，如表3所示.当干馏炉转速分别为6.8 r/min、10 r/min、13.3 r/min、17 r/min时W均大于0.887，所以认为在这几个转速下，示踪颗粒在干馏炉内的停留时间服从正态分布.当转速为3.4 r/min时，虽然W<0.887，但仅相差0.01.随着转速的提高，W值不断增加.即转速越高，示踪颗粒在干馏炉内的停留时间数据与正态分布拟合得越好.因此，得到的结果与文献[27]中的实验结果吻合较好.

表3 各工况下的夏皮罗-威尔克法W值

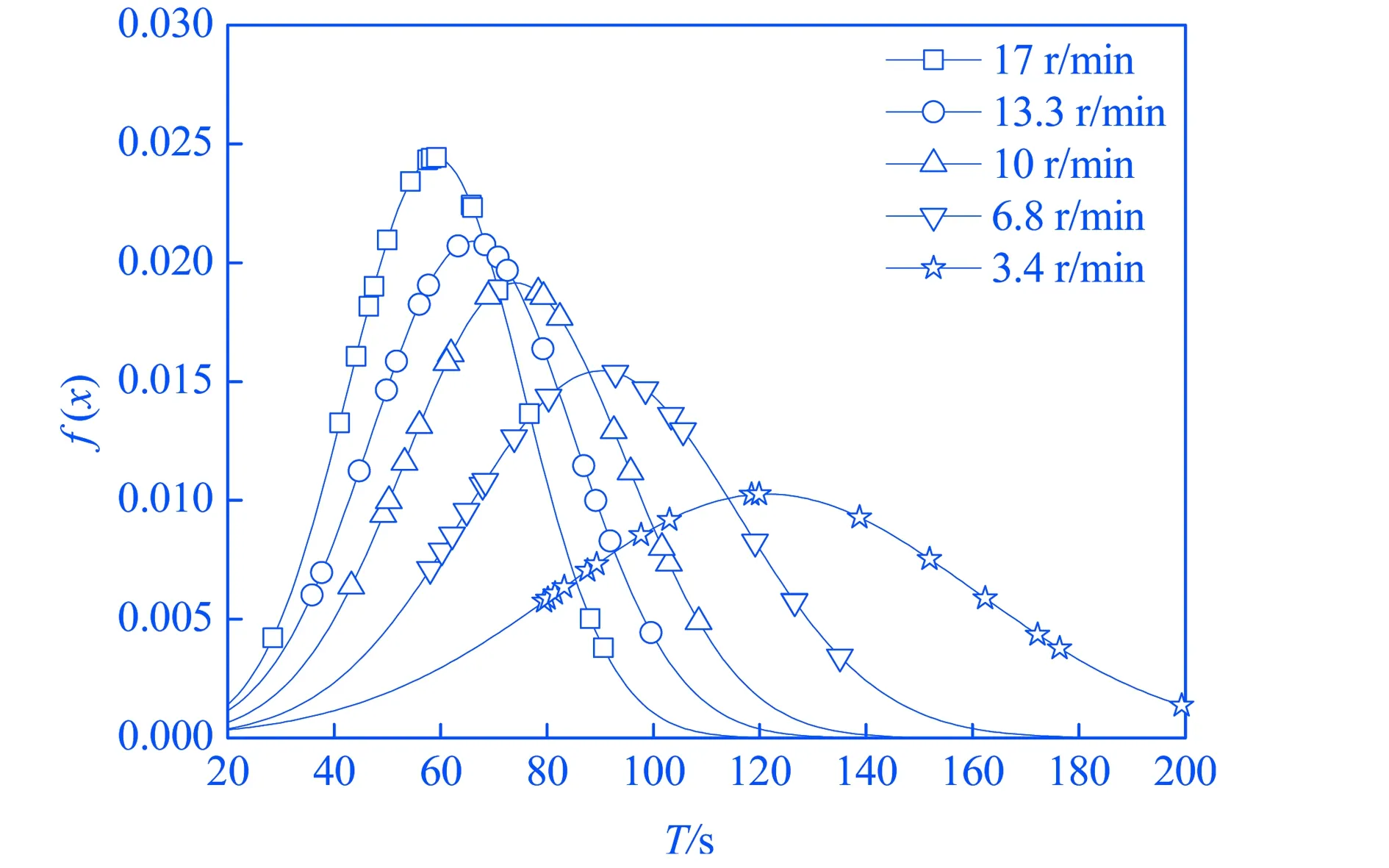
图4 各工况下颗粒停留时间概率密度比较

因为3.4 r/min时，W与0.887相差很小，为方便与其他转速下的颗粒停留时间进行比较，将3.4 r/min时的颗粒停留时间分布作为正态分布来处理.采用正态分布概率密度公式(7)[29]来分析颗粒在回转干馏炉内运动的停留时间.当X服从参数为μ，σ的正态分布时(μ为均值，σ为标准差)，其概率密度公式为

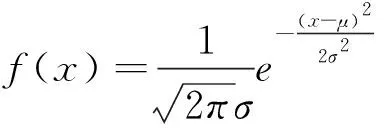
(7)

各工况下的概率密度曲线，如图4所示.图中的正方形、圆形、正立三角形、倒立三角形、星形图标不仅用来区分干馏炉转速，也代表了本文中抽取的样本，即每条曲线上的16个图标分别表示本文选取的16个示踪颗粒.可以通过曲线估计总体颗粒的停留时间分布.转速越高，曲线越陡峭，曲线的峰值越大，并且峰值向左移动.转速越高，曲线越陡峭表示转速越高颗粒停留时间的数据分布越集中，转速越低颗粒停留时间的数据分布越分散.峰值左移表示转速越高，颗粒在干馏炉内的停留时间越向较低值集中.

3 结 论

采用离散单元法，对颗粒在回转干馏炉内的运动进行了数值模拟，探讨了示踪颗粒在干馏炉内的运动规律，分析了转速变化对炉内颗粒停留时间的影响.

(1)可以将示踪颗粒在干馏炉中的运动过程分成两个阶段.第一阶段为颗粒集中阶段，第二阶段为颗粒分散阶段.干馏炉的转动和干馏炉存在倾角分别造成了示踪颗粒的径向分离和轴向分离.

(2)随着转速的提高，平均停留时间减小，其减小的程度逐渐变小，经拟合后得出转速与平均停留时间的关系近似于指数函数.

(3)转速越高，示踪颗粒在干馏炉内的停留时间数据与正态分布拟合得越好，概率密度函数最大值随着转速的增大而逐渐降低.