基于v-NPSVM的暂态稳定评估方法研究

应 鸿，姜黎莉，李 鑫，林 琳

(1.浙江华云清洁能源有限公司，浙江 杭州 310000；2.国网江苏综合能源服务有限公司，江苏 南京 210000；3.国网吉林市城郊供电公司，吉林 吉林 132001)

暂态稳定评估(Transient Stability Assessment，TSA)是电力系统安全稳定评估的重要组成部分[1].现如今，由于电力系统规模的不断扩大，网络结构和运行方式日趋复杂，保证其安全稳定运行越发重要[2].，而传统暂态稳定评估方式早已无法满足当前复杂的电网调度需求，并会给电网安全带来安全隐患[3].面对严峻的电网安全形势，研究符合当下电网运行特点且有利于电网调度把控的暂态稳定评估方法是保障电网安全的重要手段，而基于响应的故障筛选是决定暂态稳定分析在线应用效果的关键[4].

目前，基于系统响应数据的传统暂态稳定评估方法主要包括时域仿真法和直接法[5～8].两种方法都有明显的优点，其中时域仿真法适用性较强，同时能够保证较高准确性，直接法的评估速度快.但与此同时二者又有其各自的局限性.其中时域仿真法需求解大量非线性方程，计算负担较大；直接法受网络拓扑、元件模型的限制，鲁棒性较差.随着电网规模的不断扩大，复杂程度与日俱增，暂态稳定评估的重要性以及难度也随之提升，以上提到的两种传统方法已难以满足当今电网对暂态稳定评估的需求[9].而在暂态稳定评估领域有近20年研究历史的人工智能法，因其评估速度快，受系统规模和元件模型的影响小，克服了传统暂态稳定评估方法的不足.该方法通过离线训练得到系统状态变量与暂态稳定性之间的映射关系，将映射关系用于电力系统实时暂态稳定评估，在电力系统实时评估中得到广泛应用，在众多人工智能方法中，由于支持向量机具有较强的泛化能力，被广泛应用于电力系统暂态稳定评估[10～12].

支持向量机(Support Vector Machines，SVM)是基于统计学习原理用于模式分类和回归的人工智能方法[14～17].SVM现已广泛应用于人脸识别、文本分类等众多领域.近年来，支持向量机的一个衍生分类器——非平行超平面支持向量机的高速发展，引起了国内外学者的广泛关注，其中具有代表性的算法包括广义特征值近端支持向量机(GEPSVM)和孪生支持向量机(TWSVM).其中TWSVM通过求解两个较小规模QPP以替代一个较大规模QPP，此过程可以使TWSVM训练速度比标准SVC训练速度快近4倍.基于此，孪生支持向量机具有广泛应用前景.

在TWSVM的扩展研究中，大多数研究都着眼于通过原始TWSVM解决不同类型的分类问题，而缺乏寻求优于TWSVM且能够克服TWSVM不足的非并行支持向量机(Non Parallel Support Vector Machine，NPSVM).NPSVM将ε-SVR和C-SVC合并为一个模型，兼顾二者的优点，是电力系统暂态稳定评估方法的重大进步，但在NPSVM评估模型中，需要预先指定控制稀疏性的参数ε和正则化常数C，其中C取值越大代表误差越小，ε取值越大代表稀疏性越强.然而该过程严重缺乏其量化意义，无法量化暂态稳定状态的稀疏性程度，即无法对暂态稳定状态的稀疏性程度进行评估.为了改善用NPSVM进行电力系统暂态稳定评估时无法量化暂态稳定状态稀疏程度的不足，本文构造一种由v-SVC和v-SVR组成的v-NPSVM分类器，将指定参数由参数v所代替，并且能够有效控制支持向量的数量，在保证较高准确率和时间复杂度的前提下有效改善暂态稳定评估性能.并在IEEE-145节点系统中进行仿真分析、验证.

1 传统支持向量机的理论分析

1.1 v-SVC向量机

二分类问题训练样本为

T={(x1，y1)，…，(xl，yl)}，

(1)

式中：xi∈Rn为n维特征量(i=1,2,…,l)；yi∈{1，-1}(i=1，…，l)为稳定状态.标准v-SVC将问题描述为一个凸性QPP：

(2)

式中：ξ=(ξ1，…，ξl)T和v∈(0，1]分别为预测误差和先验参数.

1.2 v-SVR向量机

训练样本的回归问题：

T={(x1，y1)，…，(xl，yl)}，

(3)

式中：xi∈Rn是n维特征量(i=1,…,l)；yi∈R(i=1，…，l)是相应输出集.标准的v-SVC将问题描述为一个凸性QPP：

(4)

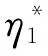
1.3 TWSVM支持向量机

二分类问题的训练样本为

T={(x1，+1)，…，(xp，+1)，(xp+1，-1)，…，(xp+q，-1)}，

(5)

式中：xi∈Rn，i=1，…，p+q.和传统SVM只拥有一个超平面不同，TWSVM通过求解一对如下小规模QPP得到两个非平行超平面(w+·x)+b+=0和(w-·x)+b-=0.

(6)

(7)

式中：ξ+=(ξ1，…，ξp)T、ξ-=(ξp+1，…，ξp+q)T和Ci(i=1，2)是惩罚参数.对于非线性分类情况，用两个二项式规划问题确定相应超平面，进而实现电力系统暂态稳定状态的辨别.

1.4 NPSVM向量机

此处介绍一种TWSVM的改进分类器NPSVM，其理论性更强并且评估准确率更高.对于训练集(5)的二分类问题，NPSVM需寻求两个非并行的超平面

(w+·x)+b+=0 和 (w-·x)+b-=0

.

(8)

求上述两个超平面，需通过求解以下两个QPP问题：

(9)

(10)

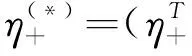
NPSVM相比TWSVM分类器具有如下优势：(1)可构造线性和非线性情况两个可被有效解决的凸QPP；(2)在训练评估模型前无需重新计算逆矩阵，并对结构风险最小化原则进行补充，适当选择参数时，可转化为TWSVM分类器.然而该过程却严重缺乏其量化意义，无法量化暂态稳定状态的稀疏性的程度，即无法对暂态稳定状态的稀疏性程度进行评估.

2 基于v-NPSVM的电力系统暂态稳定评估

2.1 原始特征集构建

本文在文献[13]的基础上构建原始特征集，通过最大相关最小冗余(mRMR)特征选择方法进行特征压缩，得到与电力系统暂态稳定特性强相关的24维特征集，如表1所示.

表1 数据集的输入特征量

系统指标由X1至X20维特征构成，投影能量函数指标X21至X24维特征构成，然后，将原始特征集随机分为训练集和测试集，使稳定与不稳定类分开，引入核函数将其映射到高维空间，将非线性分类转化为线性分类问题，用v-NPSVM进行暂态稳定评估.

2.2 v-NPSVM评估模型

鉴于用NPSVM进行电力系统暂态稳定评估时无法量化稳定状态的稀疏程度，本文构造一种由v-SVC和v-SVR组成的v-NPSVM分类器，将指定参数由参数v所代替，并且能够有效地控制支持向量的数量，在保证较高准确率和时间复杂度的前提下有效改善暂态稳定评估的性能.

(1)线性v-NPSVM

通过求解下述两个凸QPP来寻找两个非平行超平面

(11)

(12)

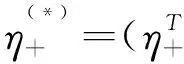
我们可以看到v-NPSVM是v-SVC和v-SVR模型的自然组合，可以用R2几何形式作为一个例子来讨论原始问题(11)，如图1所示.首先，我们希望稳定类“+”尽可能多地位于超平面(w+·x)+b+=ε和(w-·x)+b-=-ε(红色细实线)之间的ε边，它是由v-SVR实现的稳定类特征量，输出值为0(目标函数的前两项和前三个约束);其次，与TWSVM相似，我们需要尽可能将不稳定类“*”从超平面(w+·x)+b+=-ρ+(红色细虚线)中推入，这是由m-SVC实现的不稳定训练点.问题(12)类似.

(2)非线性v-NPSVM

为了将线性v-NPSVM分类器扩展到用暂态稳定评估的非线性分类情况.该方法与NPSVM相似，内核函数可以直接应用于v-NPSVM的对偶问题，线性v-NPSVM很容易扩展到非线性分类器，例如核公式：

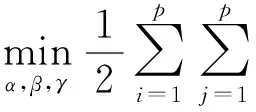
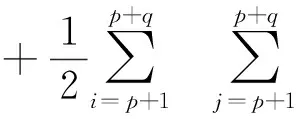
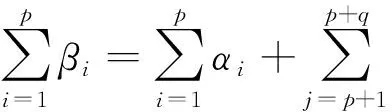
(13)

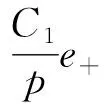
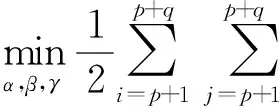
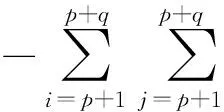
(14)

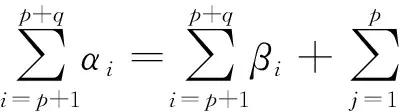
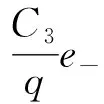
式中：K为核函数.对应的结论与线性情况相似，只是核产物(x，x′)替代了核函数K(x，x′).

基于v-NPSVM的电力系统暂态稳定评估流程：

步骤1：输入训练集(5);

步骤2：选择核函数K(x，x′)，相应参数vi∈(0，1]，i=1，2，3，4和Ci>0，i=1，3；

步骤3：分别构造和解决两个凸QPP(13)和QPP(14)，进而得到解(α，β，γ)；

步骤4：构造两个决策函数

(15)

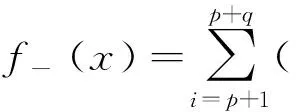
(16)

步骤5：对新输入特征x，把它分配给k类(k=-，+)，通过

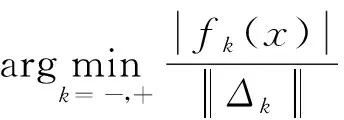
(3)参数v的重要性

参数v值是支持向量速率的下限.假设支持向量的数量是q，那么q/l≥v总是正确的，其中l是训练集中实体的数目.不同v值时的支持向量占比，如图2所示.

从表1和图9中可以看出，单点定位中方位角和俯仰角波动维持在一个较小的范围内，而距离的检测则存在20%左右的误差，通过数据融合的方式能够有效地降低距离检测误差，优化定位系统的检测能力。

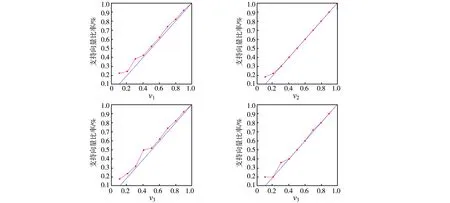
图2 不同v值时的支持向量占比

图2表明了v-NPSVM模型中支持向量vi(i=1，2，3)，4随不同参数变化的百分比，红线代表SVs的真实百分比，蓝色的是vi(i=1，2，3，4)的值.参数以0.1的步长在[0.1，1]的范围变化，我们可以看到在所有情况下，参数v都是SVs率的下限.因此如果我们想要控制SVs率，因此选择合适的v值，可以有效控制模型的稀疏性.

(4)稀疏性分析

首先，我们将v-NPSVM应用到鸢尾属植物数据集中，包含紫罗兰色和维吉尼卡两类以及包含关于类的大部分信息的两个特性，即花瓣长度和花瓣宽度.数据的分布如图3和图4所示，图中“+”s和“*”s分别代表不同类型的紫罗兰色和维吉尼卡.

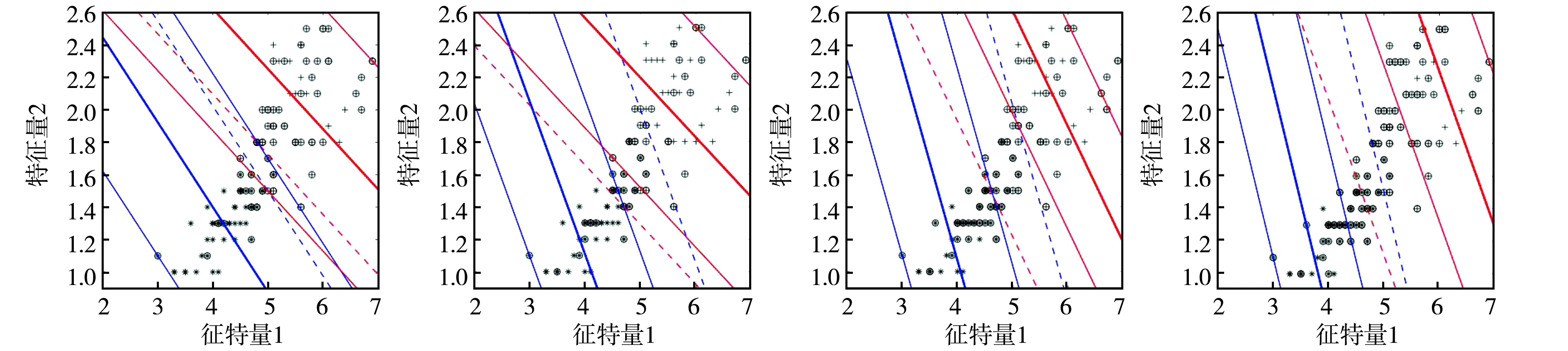
(a)v=0.1 (b)v=0.3 (c)v=0.5 (d)v=0.7图3 线性核函数的稀疏性情况

(a)v=0.1 (b)v=0.3 (c)v=0.5 (d)v=0.7图4 RBF核函数的稀疏性情况

线性内核和RBF内核单独使用，其中参数C1=150，C3=15，v1=v2=v3=v4=v以0.2的步长在[0.1，0.7]的范围内变化.图3和图4显示了实验结果，其中描述了两条邻近线f+(x)=0(红色粗实线)和f-(x)=0(蓝色粗实线)，四条ε边界线f+(x)=±ε+(红色细实线)和f-(x)=±ε-(蓝色细实线)，两条边界线f+(x)=-ρ+(红色细虚线)和f-(x)=ρ-(蓝色细虚线)，通过“.”来标记支持向量.不同v值时支持向量的数目会随之减少，并v总是位于支持向量率的下界，线性和非线性情况的稀疏性增加.

2.3 暂态稳定评估流程

依据上述方法，本文所提的系统暂态稳定评估流程分为三步：1)原始特征集构建，用mRMR对系统指标和投影能量函数指标组成的原始特征集进行特征压缩，搜索最优特征集，分成训练集和测试集，将训练集分成稳定类和不稳定类，并映射到高维空间；2)通过参数选择寻找最优参数；3)基于v-NPSVM的电力系统暂态稳定评估，生成评估模型，计算在线评价指标值.

3 算例分析

为验证本文所提方法的有效性和准确性，本文分别采用IEEE-145节点系统为例进行仿真分析，验证所提方法的准确性和有效性.

3.1 IEEE-145节点系统的原始样本集构造

IEEE-145节点系统共有50台发电机、145条母线、453条线路组成[18]，节点139所连发电机为平衡机，基准功率为100 MVA，基准电压为100 kV.发电机采用经典模型，负荷采用恒阻抗模型，故障类型为三相短路单侧主保护拒动故障，故障开始时刻是0.1 s，单侧故障清除时刻为0.2 s，不同负荷水平和不同发电机出力下，随机设置N-1故障位置，用DSP-BPA进行电力系统仿真计算来获得相应数据.共获得2000个样本，随机选取1000个作为训练集构造在线训练模型，其余作为测试集进行在线暂态稳定评估获得在线评价指标.采用所有发电机的相对功角差最大值Δδmax为暂态稳定与否判据(Δδmax≥360°系统失稳，Δδmax<360°系统稳定).稳定类和不稳定类转子角度随时间变化曲线，如图5、图6所示.

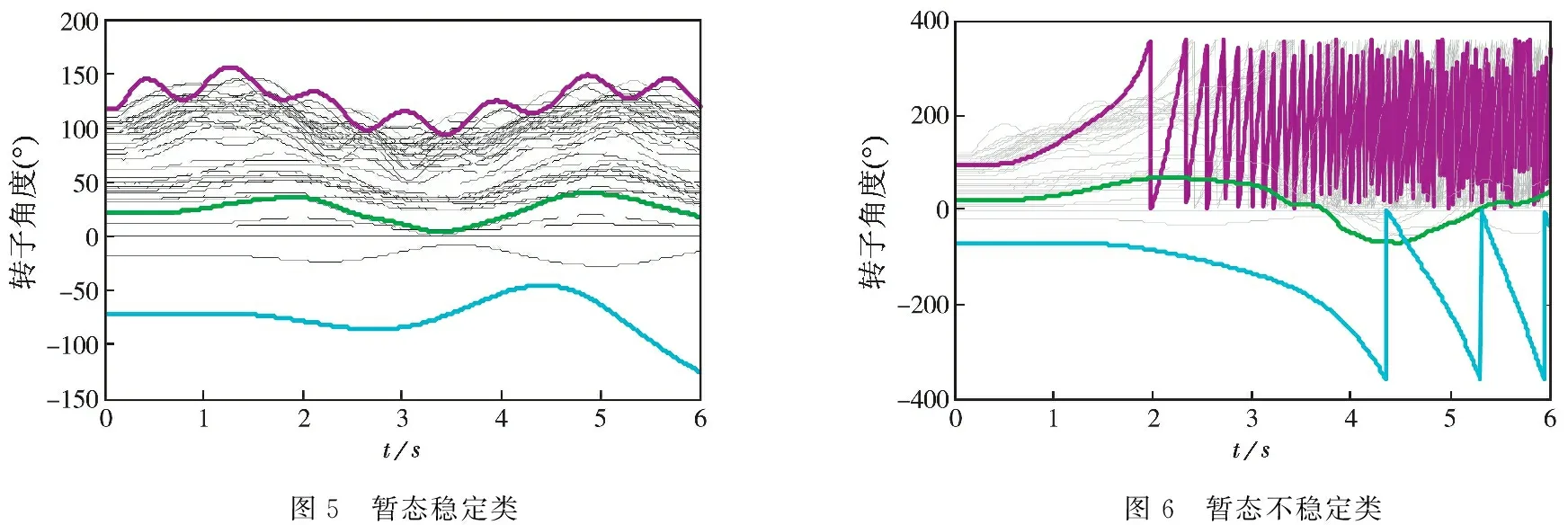
图5 暂态稳定类图6 暂态不稳定类

3.2 IEEE-145节点系统的暂态稳定评估性能分析

表2 3种分类器的评价指标

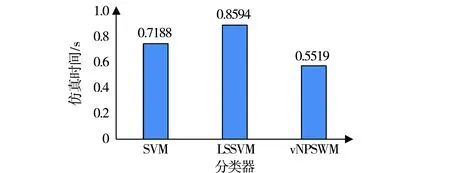
图7 3种分类器的仿真时间

核函数准确率/%Time/slinear90.560.7431poly92.540.9805RBF93.120.5519

通过对比表2中3种分类器的准确率指标、ROC指标、Kappa指标，综合评价指标，可知v-NPSVM的准确率指标为93.12%另外两种支持向量机的评估性能.而且v-NPSVM在评估过程中所需计算时间为0.551 9 s较低，因此v-NPSVM在保证分类器具有较高评估精度的同时，具有较低的时间复杂度.3种分类器的仿真所需时间对比情况，如图7所示.

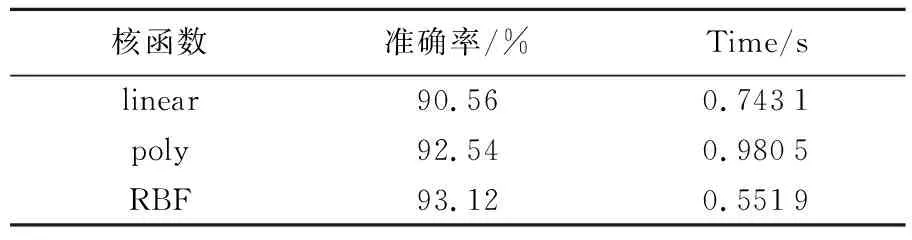
(2)v-NPSVM的核函数分析，考虑3种核函数对v-NPSVM算法评估精度及评估准确率的影响，不同核函数的评估性能如表3所示.

由表3可知，径向基核函数的评估准确率为93.12%高于线性和多项式核函数，在时间复杂度上径向基核函数0.551 9 s低于其他两种核函数.综合考虑评估准确率和时间复杂度两个重要指标，径向基核函数为v-NPSVM分类器的最佳核函数.

(3)为进一步分析不同v值对评估模型的影响将稳定类与不稳定类的投影坐标信息，如图8所示.

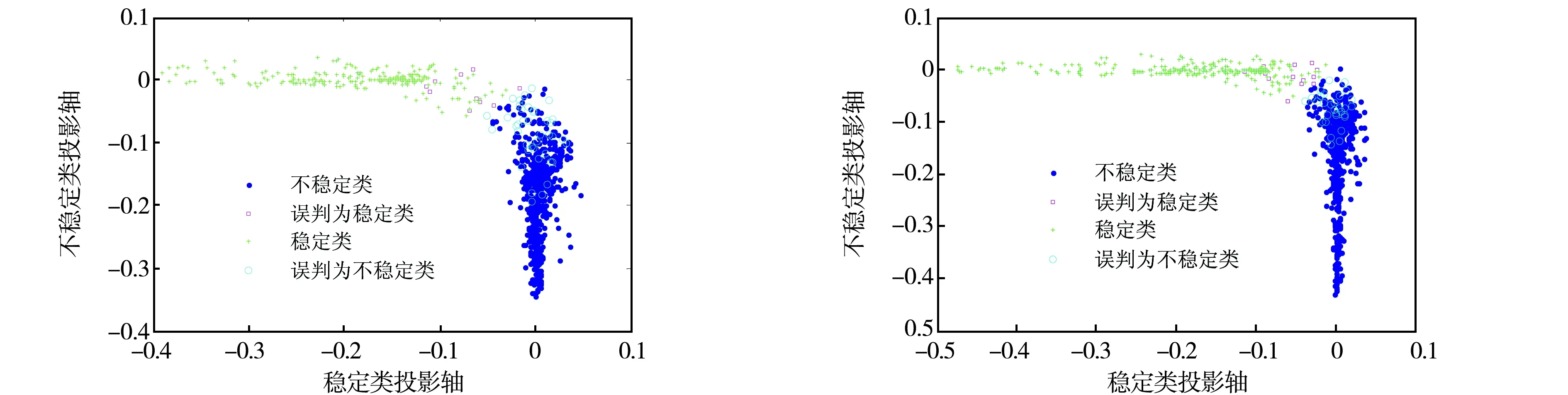
(a) v=0.5 (b) v=1.0图8 IEEE145系统不同v是的分类结果

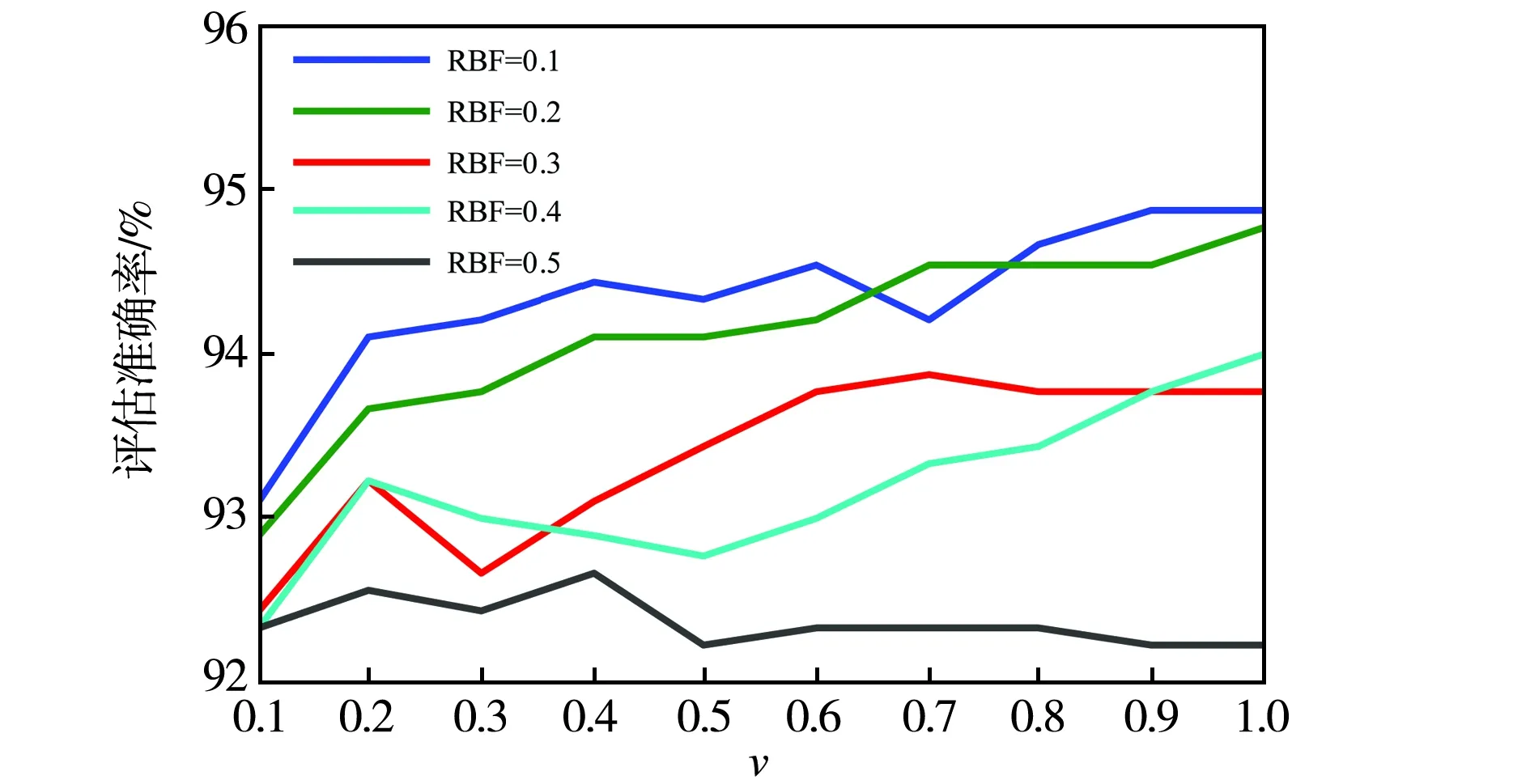
图9 IEEE-145系统不同核参数和v值的评估准确率

图8中稳定类用绿色“+”表示，不稳定类用蓝色“·”表示，稳定类被误判为不稳定类的样本用天青色“○”表示，不稳定类被误判为稳定类的样本用粉色“□”表示，黑色斜线为分类线.由图8可知，不同v值对电力系统暂态稳定评估准确率具有一定的影响，而且v值的改变可以改变评估数据的稀疏程度，即支持向量的个数，进而改变评估精度，可见v合理取值可有效改善评估性能，下面将着重分析不同v值及不同核参数时对评估准确率的影响.

(4)不同v值及核参数对评估准确率的影响.首先分析不同v值对评估准确率的影响，如图9所示.

由图9可知，核参数在[0.1 0.2]之间时能够保证较高的评估准确率，但不同核参数的暂态稳定评估稳定性及计算时间不同.当RBF=0.5时，评估准确率随着v值的变化而上下震动，准确率在92.2左右，计算时间分别为88.36 ms；当RBF为[0.1 0.2 0.3 0.4]时，准确率随v值的增加而增加，计算时间为66.98 ms.可见当核参数RBF=0.1时具有较好的评估性能.而且v值的变化对电力系统暂态稳定评估性能具有较大影响

4 结 论

本文提出一种基于v-NPSVM的电力系统暂态稳定评估方法，并通过IEEE-145对所提方法的准确性和有效性进行验证，相关结论如下：

(1)样本集构建方面采用系统指标和能量函数指标相结合的方式，可有效表征系统的稳定性，降低特征集维数和减少冗余信息，并合理选择核参数可有效改善评估模型的暂态稳定评估精度.

(2)v-NPSVM分类器通过使用参数v替代现有支持向量机的参数C，可有效平衡传统支持向量机的的两个目标，即最大限度地提高了边缘值并最小化了训练误差，与NPSVM模型中的参数C相比，v具有更精确的量化意义，v值是支持向量占比的下限，可通过合适的选择v值来控制v-NPSVM模型中SVs的速率，利用不同的参数v可以获得不同的稀疏性，从而启发我们解决不平衡的分类问题.