ATIS环境下的网络交通流逐日动态演化研究

阎 昊,刘诗序,杨少辉,陈文思,郭丽丹,唐颖诺,方 捷

(1. 福州大学土木工程学院,福建 福州 350116； 2. 中国城市规划设计研究院,北京 100037)

0 引言

当今,交通问题日益显著,特别是对于许多大城市来说,交通拥堵严重困扰了人们的日常出行,已引起政府、通勤者和相关研究人员的广泛关注. 随着大数据和智能化的迅猛发展,作为智能运输系统重要组成部分的先进的出行者信息系统(advanced traveler information systems,简称ATIS)被越来越多的研究工作者所考虑,这也使得研究出行者择路行为成为交通领域的热门问题之一.

ATIS实施的效果取决于ATIS发布的信息影响人们的出行行为,信息作用下的出行者出行行为的相关科研成果丰富,Ben-Elia等[1]系统总结交通信息对出行行为(主要包括出行方式选择和出行路径选择)的影响,信息对个体出行行为会产生有益作用,但是对网络集计行为的影响尚无定论. 每个出行者出行选择结果集计到交通网络上就形成网络交通流,同时,因为出行者具有习惯性和学习能力,出行者的出行选择也会受到历史选择结果的影响,在信息和出行经验共同作用下,出行者每天的出行选择可能会不同,在宏观上的体现就是网络交通流的演化.

交通信息对网络交通流演化的影响,目前国内外学者进行很多研究. 交通历史信息的研究有Cascetta等[2-3]建立day-to-day和within-day择路模型,发现交通信息会使交通流持续波动,而出行者的个人经验能够使交通流平稳. Sun等[4]研究表明,利用交通历史信息可以提高行程时间的可靠性. Selten等[5]借鉴经济学实验方法,选取18个大学生为实验对象,其中只有9人可以获得完全历史信息,其余9人只能获得部分历史信息,在2条平行路径的路网中完成择路行为实验. 结果发现波动现象始终贯穿于整个实验,但是获得完全历史信息会显著减小这种波动现象. Kim等[6]基于Agent仿真模型,分析UE条件对路网交通流演化的影响,研究结果得出,完美信息和先验信息对路径选择有很大的影响. Wang等[7]用元胞自动机模型研究信息影响下的双通道决策问题,提出合理利用交通信息的建议. 田丽君等[8]借助一个包含两条路径的非对称简单路网,运用元胞自动机模型模拟两种信息反馈策略下的日常路径选择的演化过程. 交通预测信息方面的研究有刘诗序等[9]运用微观仿真的方法,探讨预测信息对出行者择路行为以及网络交通流演化的影响,发现出行者对预测信息的偏好程度和相关模型参数都会影响网络交通流的波动性和系统效率. 刘天亮等[10]提出路网信息公开与否的两种路径更新规则,通过数值实验研究得出,发布信息使路径流量更快地收敛到SUE均衡态. 郭仁佣等[11]建立ATIS作用下多用户参与并且多准则决策的SUE交通流演化模型,运用Brouwer不动点定理证明模型固定点的存在性,可惜的是,并没有分析ATIS市场占有率对网络交通流演化的影响. 最近,文献[12-13]研究社交网路信息对出行行为的影响.

从现有的研究成果可以看到,目前还缺乏对交通网络中只有部分出行者具有ATIS设施的网络交通流演化的深入研究,即交通网络中部分出行者依靠历史经验和ATIS信息出行,另一部分只能凭借历史经验出行,在这种情况下,ATIS市场占有率(具有ATIS设施的出行者占出行者总量的比例)对网络交通流逐日动态演化有着什么样的影响需要深入探索. 需要说明的是,ATIS市场占有率对网络交通流静态均衡分配的影响早有研究,文献[14-15]做了许多相关的工作. 实际上,由于每天出行者的择路行为是一个巨量出行者参加的动态博弈过程,故而网络交通流不会始终如一,而是呈现出动态演化过程. 不同ATIS市场占有率下,网络交通流将会呈现出怎样的逐日动态演化规律,正是本文研究的内容,本文以出行者个体为对象,通过数值实验,研究ATIS市场占有率对出行者路径选择的影响,分析网络交通流的演化规律.

1 模型的建立

如图1,出行者每天的路径选择流程如下： 首先,出行者分为具有ATIS设施和不具有ATIS设施两类,具有ATIS设施的出行者可以获取路网的全部信息,不具有ATIS设施的出行者,只了解自己所选出行路径的历史信息,其余路径的信息并不知晓. 而后,出行者依据这些信息去预估第二天路径的行程时间,也就是感知行程时间,出行者再根据感知行程时间和路径选择模型进行路径选择. 每个出行者选择路径出行后,汇集到路网上生成路径流量,根据路径-路段的关联关系以及交通流模型,计算出路段和路径的实际行程时间,作为信息发布给出行者[9].

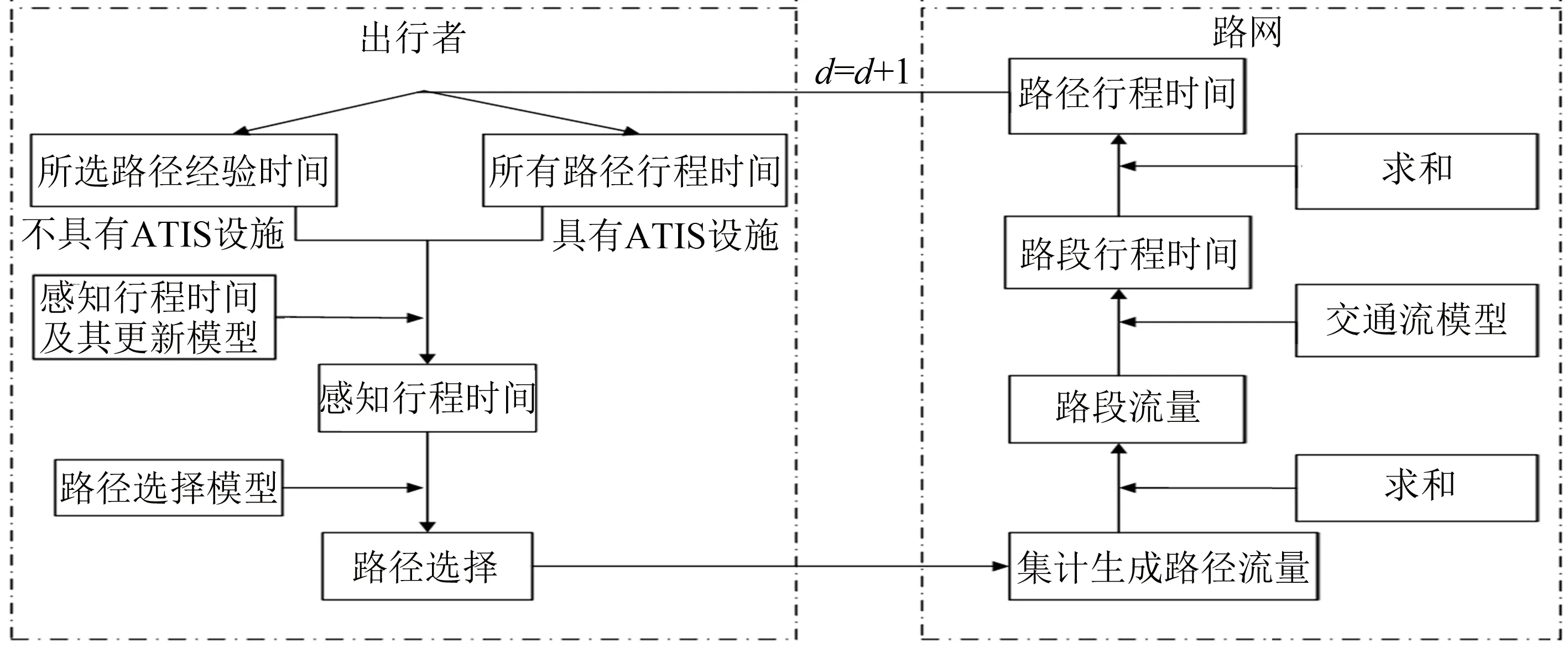
图1 出行者逐日路径选择过程 Fig.1 Travelers’ day-to-day route choice process

1.1 出行者路径选择模型

出行者在日常的出行中,由于不确定情况(如天气变化,交通事故等)很难精准地预先获知路径行程时间,出行者只能根据自己的感知行程时间选择路径[9],假设出行者i第d天对路径k的感知行程时间为：

(1)

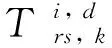
假定随机项ξ服从均值为零的二重指数分布,且每条路径的随机项互相独立. 如果rs之间含n条路径,按照效用最大化准则,出行者i第d天选择路径k的概率为：

(2)

式中：θ反映出行者在择路时的随机性,与感知行程时间随机项ξ的方差有关,ξ的方差越大,θ越小,说明出行者在择路时的随机性越大,反之亦然.

从式(2)可看出,出行者选择任意一条路径的概率与对该路径的感知行程时间相关.

1.2 出行者逐日路径选择学习模型

ATIS市场占有率γ表示具有ATIS设施的出行者比例,γ越大,具有ATIS设施的出行者人数就越多. 分别建立不具有ATIS设施和具有ATIS设施的出行者感知行程时间更新模型.

1) 不具有ATIS设施的学习模型. 不具有ATIS设施的出行者只能按照自己的历史出行经验预测第二天的感知行程时间,第d+1天的感知行程时间期望值表示为第d天感知行程时间期望值和实际行程时间的加权平均,未选择路径的感知行程时间期望值保持不变,更新模型为：

(3)

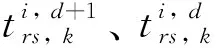
2) 具有ATIS设施的学习模型. 当出行者具有ATIS设施时,ATIS会发布所有路径的出行信息,第d+1天的感知行程时间期望值根据第d天感知行程时间期望值和实际行程时间来更新：

(4)

式中：ρ为权重系数； 其余符号含义同式(3). 权重系数ρ的含义和φ相同.

2 基于MATLAB的数值实验

2.1 场景设计

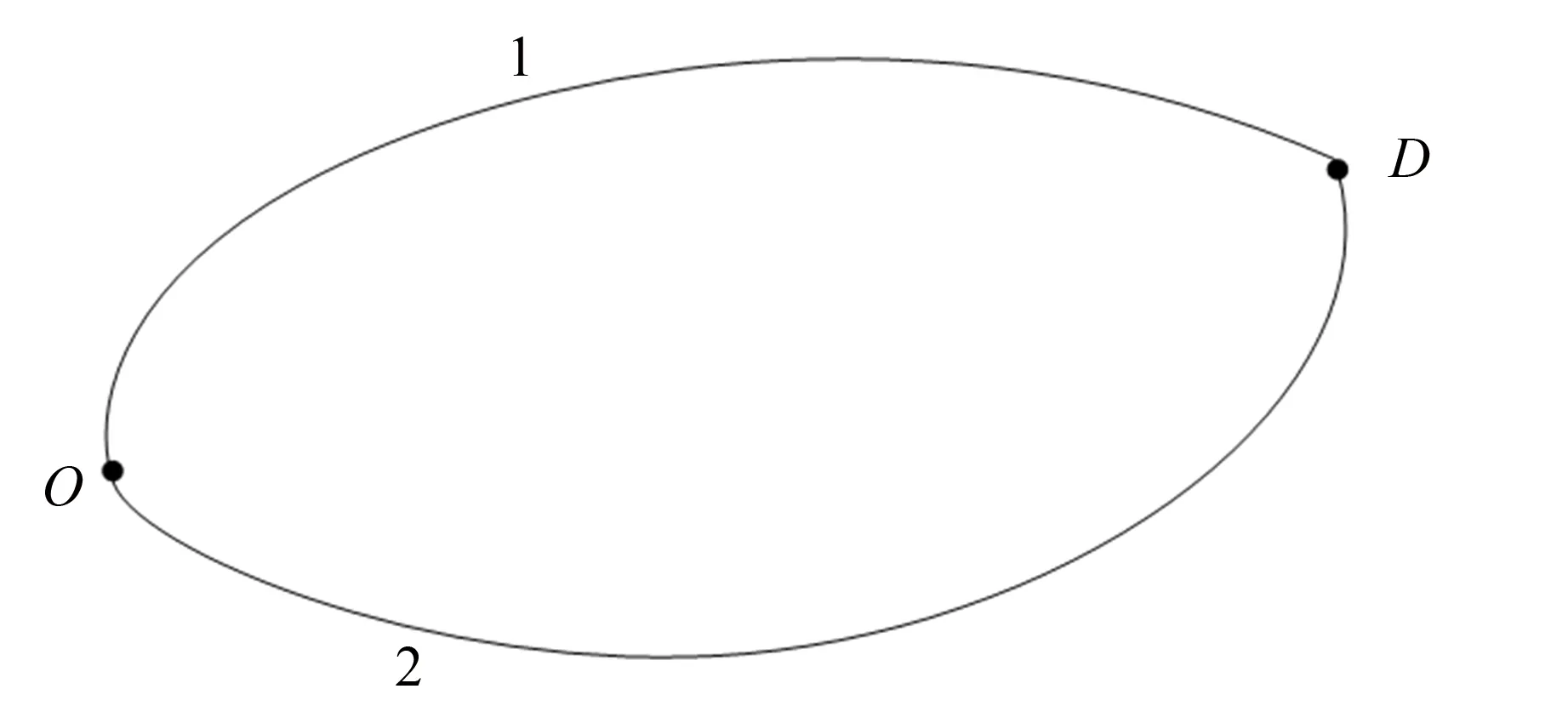
图2 路网示意图Fig.2 Road network diagram

如图2所示,数值实验使用只有2条路径的简单路网，路段阻抗函数是t=tf[1+0.15(q/C)4)], 其中tf表示路段的初始自由流行程时间,q表示路段流量,C表示路段通行能力. 参考文献[16]的实验路网,确定本文的数值实验参数取值. 路径1：tf1=22 min,C1=150辆·h-1； 路径2：tf2=25 min,C2=200辆·h-1. 出行者人数为N=200,具有ATIS设施的人数为N·γ. 设实验天数为M=1 000 d，对200个出行者每日的出行选择进行数值实验.

2.2 实验结果分析

运用MATLAB软件,基于logit随机用户均衡分配模型,便可算出出行者不同随机程度(即不同的θ值)对应的路径流量分配结果,表1以路径1为例给出了路径流量结果,当θ≥1.75时,流量不再显著变化.

表1 路径1上的logit随机用户均衡流量

在数值实验中,θ取1.75,对参数φ、ρ、γ取不同值时进行模拟实验,分析路径流量的波动情况. 下面分别对φ、ρ的同步变化和γ的变化两类情形进行讨论.

1)γ取值固定,φ、ρ同步变化.γ=0时各统计结果如图3所示.γ=0时,表示所有出行者都不具有ATIS设施,图3(a)中路径1流量均值在φ和ρ从0～0.3变化过程中,迅速增长,说明出行者受昨日所走路径的实际时间影响较大,φ和ρ从0.30～0.99变化过程中,均值变化明显减缓,逐渐趋于SUE稳定态,当φ=ρ=1时路径1流量均值突变到接近于200,但是已超过路径1容量,说明该特殊情况下路径1处于非常拥堵的状态； 流量标准差在φ和ρ从0～0.3变化过程中,基本接近于0,在0.3～0.7之间,标准差先增大后减小,系统有一些振荡,φ和ρ在0.7以后,又基本趋于稳定并逐渐减小至0,系统又恢复稳定. 从φ=ρ=0.7开始,基本稳定在SUE均衡态(如图3(b)).

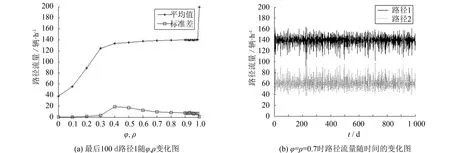
图3 γ=0时路径流量变化图Fig.3 Route flow varying when γ=0

γ=0.5、1.0时统计结果如图4所示.γ=0.5时,表示只有一半出行者具有ATIS设施,由图4(a)可知,流量均值大体呈上升趋势,从φ=ρ=0.55开始,已基本达到随机用户稳态值了； 标准差的变化是φ和ρ从0～0.99变化过程中,先增后减,在φ=ρ=0.4时达到最大值. 当φ=ρ=1时,路径1流量均值发生突变.

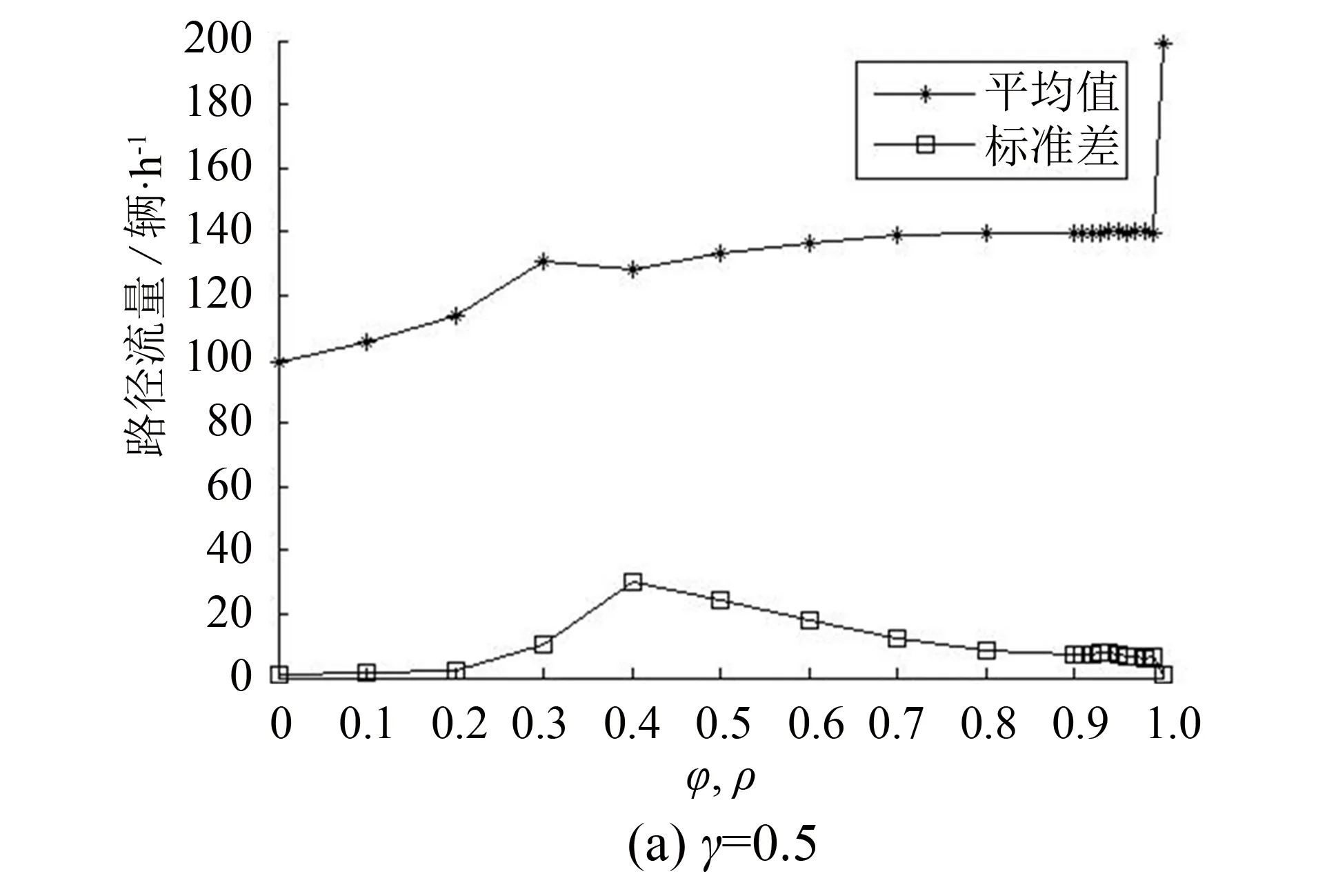
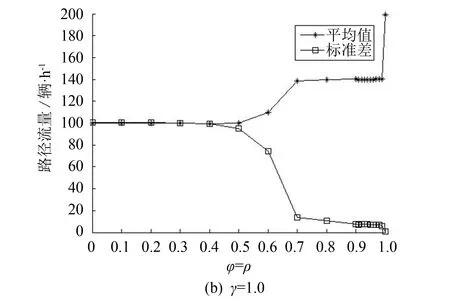
图4 最后100 d路径1的流量均值、标准差随φ, ρ变化图

γ=1.0时,表示所有出行者都具有ATIS设施,完全知道历史信息. 如图4(b),φ和ρ在0～0.5范围内,均值和标准差都在100左右,流量振荡比较厉害,说明出行者对ATIS提供的历史信息依赖比较严重,没有自己的惯性和主见,盲目地信赖ATIS的指示,每天都改变路径,从而无法达到一个路径选择的稳定态.φ和ρ在0.5～0.8时,均值和标准差波动较大,路径流量开始趋向于稳定状态,标准差也明显减小.φ和ρ从0.8变到0.99过程中,流量基本稳定到SUE均衡态. 当φ=ρ=1时会发生突变.

2)φ、ρ取值固定,γ不断变化.φ、ρ取不同的值,最后100 d路径1的流量均值和标准差随γ变化统计结果如图5所示.

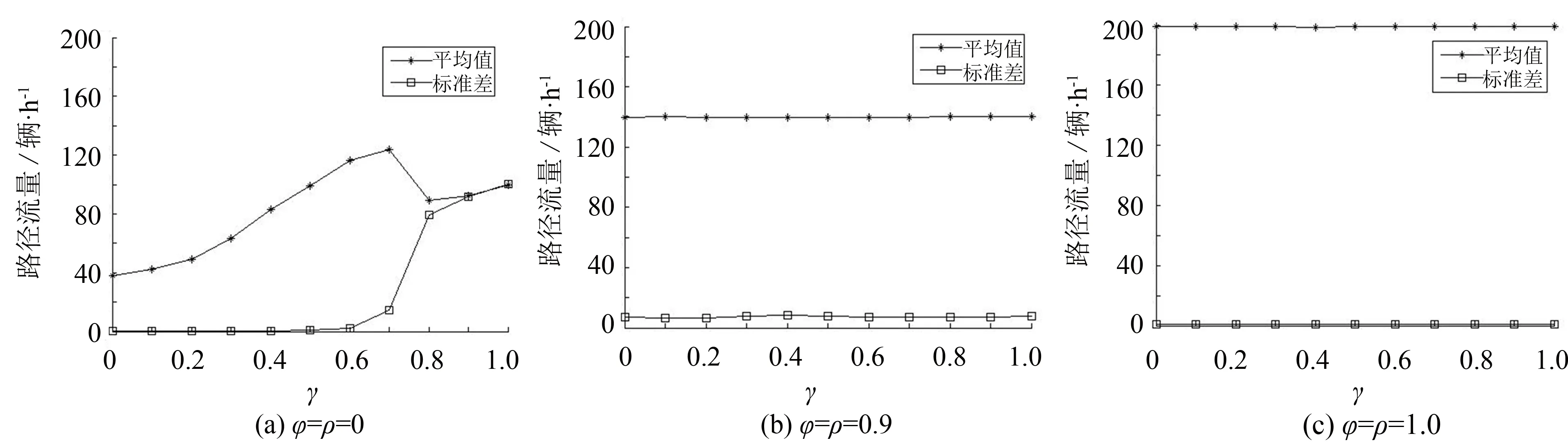
图5 φ, ρ取值固定最后100 d路径1的流量均值和标准差随γ变化图Fig.5 Mean and standard deviation of route 1’s flow varying with γ in the last 100 days when φ, ρ take fixed values

①φ=ρ=0, 表示出行者完全依赖历史信息,如图5(a)所示,γ从0～0.7变化过程中,具有ATIS设施的出行者的比例越来越大,流量均值不断增大,γ在0.7～1.0之间,均值先减小再增大,始终偏离SUE均衡态. 标准差在γ从0～0.6变化过程中,基本接近于0,此后增大明显,系统越来越不稳定.

②φ=ρ=0.8、0.9时,情况类似,以φ=ρ=0.9为例说明. 如图5(b)所示,γ从0～1变化过程中,具有ATIS设施的出行者人数从0变到200,流量均值基本没有变化,始终稳定在SUE均衡态附近； 流量标准差也基本没有波动,表明系统非常稳定. 由图可知出行者对感知行程时间的依赖程度较高,对实际行程时间的依赖程度较低,并且90%的出行者具有ATIS设施时,路网流量演化的效果最优.

③φ=ρ=1.0时,表示出行者出行选择都依据前一天的感知行程时间,每一天都等于初始自由流时间,如图5(c)所示,在0～1范围内,无论γ取何值,路径1流量均值都接近于200,标准差都接近于0,网络交通流演化稳定.

综上所述,信息依赖程度和ATIS市场占有率对出行者的出行行为以及路网流量演化的影响呈现以下规律： 当出行者完全依赖历史信息出行(即φ=ρ=0),路径流量始终偏离随机用户均衡态,且流量从平稳变得越来越振荡； 当出行者对感知行程时间的依赖程度超过了90%,网络交通流演化稳定. 当ATIS市场占有率在50%以内时,随着出行者对昨日感知行程时间的依赖程度φ和ρ的增大,路径流量逐渐趋近于随机用户均衡态； 当ATIS市场占有率为100%时,出行者对昨日感知行程时间的依赖程度不同,网络流量呈现出截然不同的状态.

3 结语

1) 网络交通流演化是否稳定,以及能否达到SUE均衡态,与出行者对昨日感知行程时间的依赖程度φ、ρ以及ATIS市场占有率γ两者都有关系. 当出行者对昨日感知行程时间的依赖程度为80%～99%时,无论有多少出行者配备ATIS(即φ=ρ=0.8～0.99,γ取0～1时),路径流量都能演化到SUE均衡态,路网系统比较稳定,不会发生振荡. 其他情况无法达到SUE均衡态.

2) 当出行者对昨日感知行程时间的依赖程度从很大(即φ、ρ接近1,但不等于1)变化到完全依赖(即φ=ρ=1)时,无论ATIS市场占有率γ取任何值,路径流量演化都会发生突变； 当出行者完全依赖昨日实际行程时间(即φ=ρ=0)时,路网系统始终偏离SUE均衡态.

3) 当出行者对昨日实际行程时间完全不依赖(即φ=ρ=1)时,出行选择都依据前一天的感知行程时间,每一天的感知行程时间都相等并且等于初始时间,无论有多少出行者配备ATIS(即γ取0～1任意值)时,出行者集中选择同一路径,该条路径的流量均值接近OD总量,并且网络交通流演化稳定.

4) 当ATIS市场占有率为0%和50%(即γ=0、γ=0.5)时,对网络交通流演化情况的影响相似,随着出行者对昨日感知行程时间的依赖程度φ、ρ的增大,路径流量逐渐趋近于随机用户均衡态,且流量震荡幅度不大； 而当ATIS市场占有率为100%时,出行者对昨日感知行程时间的依赖程度在50%以内时(φ、ρ取0～0.5),路径流量偏离随机用户均衡态,且流量振荡幅度非常大,出行者对昨日感知行程时间的依赖程度超过80%时(φ、ρ取0.80～0.99),路径流量基本稳定在随机用户均衡态.