布金汉方程一般解在测流变参数的应用

朱 旦 生

(甘肃省兰州市灌溉试验示范中心， 兰州 甘肃 730000)

非牛顿流体是剪应力和剪切变形速率之间不满足线性关系的流体。宾汉流体(也称宾汉塑性流体或宾汉塑料)，是非牛顿流体的一种，通常是一种黏塑性材料，在低应力下，它表现为刚性体，但在高应力下，它会像黏性流体一样流动，且其流动性为线性的。水利行业中对宾汉体的研究始于高含沙水流流动现象的研究，20世纪黄河上、中游高含沙洪水经常遇到的“浆河”及“揭河底”现象，揭示了水利工程生产实践中同样存在宾汉体的非牛顿流体现象。由于宾汉体含沙水流形成的条件不但与浑水的平均含沙量有关，而且与极细黏性泥沙颗粒的含量高度有关，相同浓度下黏性细颗粒构成的浑水更容易由牛顿体变为宾汉体，因此在灌溉渠系的末端或者一些节水器具的特殊部位也会出现宾汉体流动现象，这对灌溉器具的研发无凝会提出更高的挑战。因此，从灌溉工程实践需求角度，宾汉体浑水的研究也具有重要意义。由于宾汉流体流变参数的确定是研究各种宾汉体问题的基础，因此本文从宾汉体流变方程的求解出发，对测流变参数的应用方面进行一些有益的探索。

1 宾汉体流变学的基本问题

宾汉体流变特性可用如下方程表示[1]

(1)

针对灌流对公式(1)分离变量积分，得到著名的布金汉方程：

(2)

当τB=0时，由公式(2)即可得出适合牛顿体的泊谡叶方程：

(3)

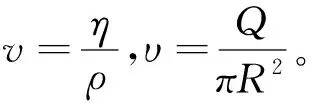
可以得出[2]

(4)

这种方法比传统方法更近了一步，可以查表得出τB和η。但随着计算技术的飞速发展，探索一种合适的数值计算方法仍有必要。

2 布金汉方程的一般解

一元四次方程可写成一般形式[3-4]

x4+P3x3+P2x2+P1x+P0=0

(5)

配方，可写成如下形式：

(6)

(7)

右边，一元二次方程要成为完全平方式，则根据判别式Δ=0，得到一个一元三次方程，称“预一元三次方程”[4]。

则一元四次方程，变成

(8)

得到两个一元二次方程

(9)

和

(10)

即得到一元四次方程一个根。

布金汉方程可化为

(11)

则布金汉方程变为

(12)

可得

得到布金汉方程的“预一元三次方程”：

(13)

无妨取最简单根：

则布金汉方程变为

(14)

则布金汉方程的四个根为

满足条件的根为

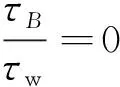
因此，符合一元四次方程四根，满足布金汉方程的解为

3 讨 论

在毛细管黏度计测极限切应力τB和刚度系数η时，更换管径D得到不同的v。由于这个方程有两个未知数τB和η，则至少要做两组实验，但由于毛细管黏度实验中有实验误差，故一个样品要做多组实验，取误差小的数值。通过联立如下方程组可以求得：

(15)

4 结 论

本文通过用一元四次返程求根法得出布金汉方程的一般解。这个一般解可用于求宾汉体流变参数极限切应力和刚度系数。作为一种科学探索，本文的研究方法理论严密，且可为从事宾汉流体工程问题研究的科技工作者提供实际应用。