外场调制控制环形腔光折变 振荡器的时空混沌
周绣佳, 冯秀琴, 张志颖, 姚治海, 王晓茜
(长春理工大学 理学院, 长春 130022)
时空混沌是非线性系统特有的一种状态, 广泛存在于自然界中. 光学时空混沌是非线性光学系统普遍存在的现象, 目前, 有关激光器的时空动力学行为[1]、 环形腔激光器系统[2-4]、 光学双稳态系统[5-7]、 光学相位共轭[8]、 光学参数振荡器系统以及光折变振荡器系统的时空混沌已取得很多研究成果[9-14]. 自White等[15]实现光折变振荡器以来, 环形腔光折变振荡器的非线性动力学研究已引起人们广泛关注, 如利用微分方程对合作频率锁定[16]、 横模巡游[17]、 光学斑图和时空混沌[18-19]以及对称耦合条件下光折变振荡器的时空混沌控制与同步[20-21]等. 本文在此基础上, 研究非对称耦合条件下二维时空混沌的控制.
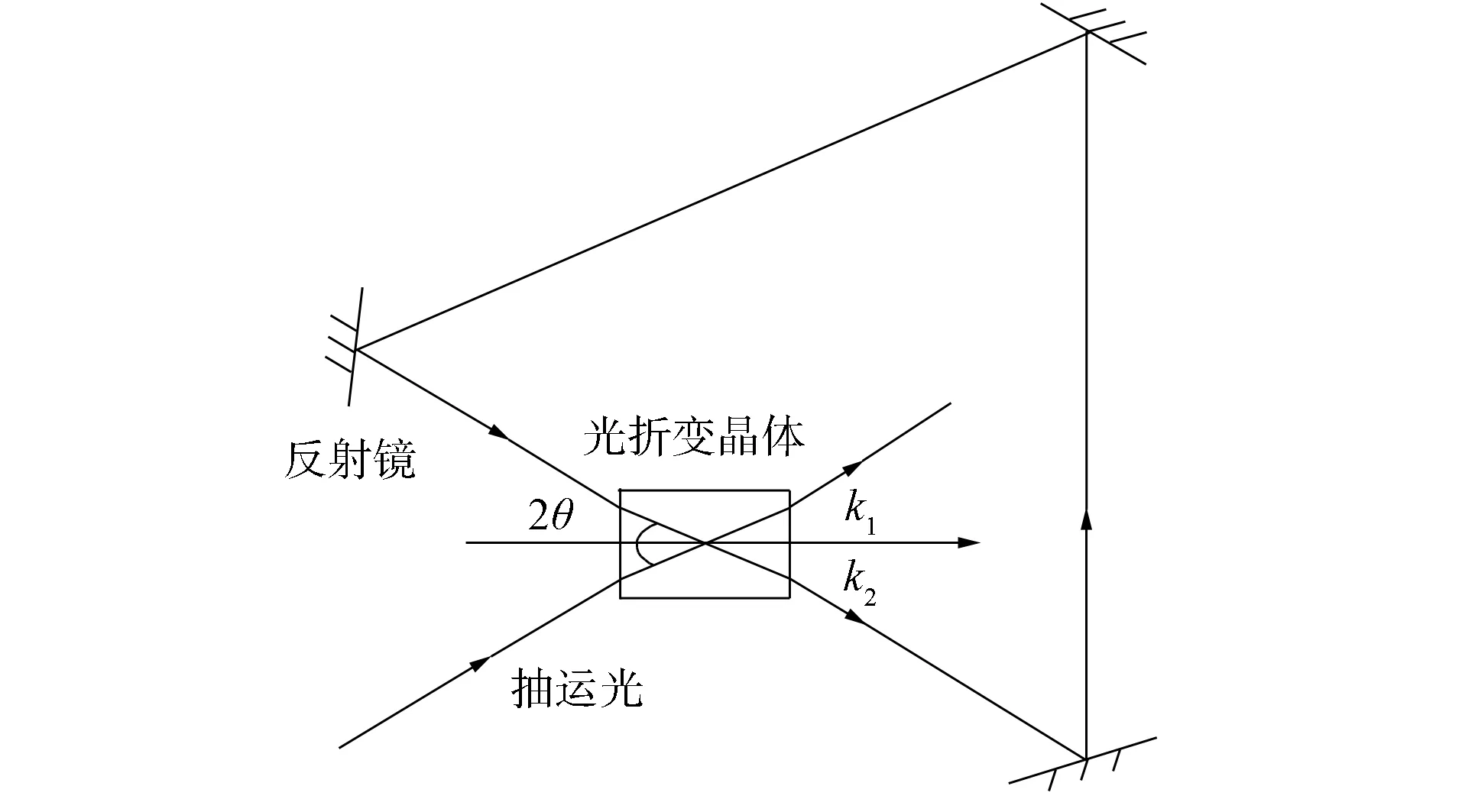
图1 环形腔光折变振荡器原理Fig.1 Schematic diagram of photorefractive ring oscillator
1 非对称耦合环形腔光折变振荡器的时空混沌
环形腔光折变振荡器原理如图1所示, 对应的系统动力学行为可由如下迭代方程表示[13,22]:
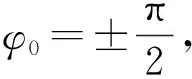
非对称耦合二维时空动力学方程为
其中:n为迭代步数;i,j=1,2,…,L为二维空间平面坐标;εm(m=1,2,3,4)为空间相邻格点间的非对称耦合系数; 函数f[In(i,j)]表示系统的局域动力学函数, 用方程(1)~(3)表示;In(i,j)为状态变量, 表示信号光强.
初始条件为除激光光源外没有其他光场存在的均匀分布的空间光场,I0(i,j)=0.3, 系统参数为
(8)
非对称耦合系数分别为
ε1=0.05,ε2=0.06,ε3=0.055,ε4=0.045,
(9)
边界条件为
In(0,j)=In(i,L+1)=In(i,0)=In(L+1,j)=0.
(10)
图2为第(32,32)格点的时间序列和时空演化, 其中: (A),(C),(E),(G)分别为Ωτ=0.3,0.7,1.05,1.4时格点(32,32)光强随时间的变化; (B),(D),(F),(H)分别为Ωτ=0.3,0.7,1.05,1.4时光强的横向分布. 由图2可见: 当Ωτ=0.3时, 二维空间环形腔光折变振荡器系统均匀稳定, 系统输出状态为稳定的周期1; 当Ωτ=0.7,Ωτ=1.05时, 系统的输出状态为倍周期状态, 从周期2、 周期4过渡到周期8状态; 当Ωτ=1.4时, 系统输出状态为时空混沌状态.
空间斑图与系统参数和时间有关. 当系统参数为式(8)-(9)及Ωτ=1.4, 初始条件为I0(i,j)=0.3, 边界条件为式(10)时, 由方程(7)的数值计算结果表明, 空间非对称耦合作用破坏了系统原有的对称结构, 出现对称破缺现象, 随着时间的增加逐渐向中心扩散, 最后演变为完全时空混沌状态, 如图3所示. 由图3可见: 当时间步数n=50时, 时空斑图的四角处开始出现不稳定现象; 当n=100时, 不稳定范围扩大; 当n=150时, 不稳定范围进一步向中心扩散; 当n=200时, 系统呈完全时空混沌状态.
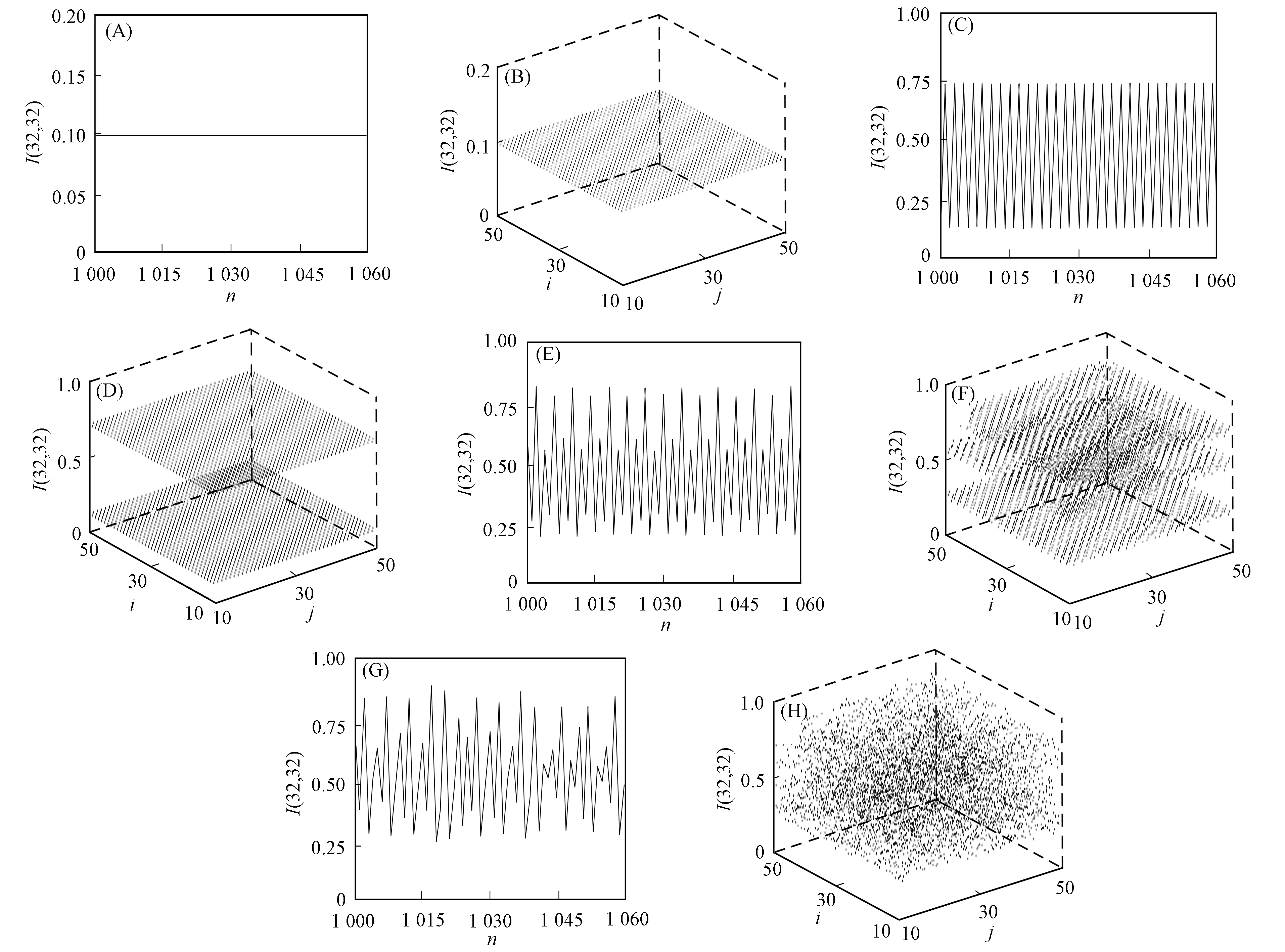
图2 格点(32,32)的横向分布及其随时间的演化Fig.2 Transverse distribution of lattice (32,32) and its evolution with time

图3 从对称破缺向光学湍流演化的横向斑图Fig.3 Transverse pattern from evolution of symmetry breaking to optical turbulence
2 非对称耦合环形腔光折变振荡器的二维时空混沌控制
2.1 均匀外场调制控制二维时空混沌
均匀外场调制控制非对称耦合环形腔光折变振荡器系统二维时空混沌的动力学方程为
其中:f[In(i,j)]为局域动力学函数;M为均匀外场调制强度;εm(m=1,2,3,4)为空间相邻格点间的非对称耦合系数. 系统参数为式(8)-(9)及Ωτ=1.4, 初始条件为I0(i,j)=0.3, 边界条件为式(10), 从n=600步开始加入控制, 结果如图4所示, 其中: (A),(C),(E)分别为M=0.07,0.15,0.41时系统输出光强度随时间的变化; (B),(D),(F)分别为M=0.07,0.15,0.41时系统输出光强度的时空分布. 由图4可见: 当均匀外场调制系数分别为M=0.07,0.15,0.41时, 系统分别被控制到周期4,2,1; 系统中每个格点输出的光强度均不随时间变化, 但不同格点输出的光强度不同.
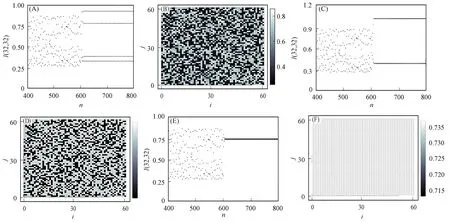
图4 均匀外场调制环形腔光折变振荡器二维时空混沌的控制结果Fig.4 Control results of two-dimensional spatiotemporal chaos by uniform external field modulation in photorefractive ring oscillator
2.2 混沌光场调制控制二维时空混沌
将环形腔激光器输出的混沌激光作为调制信号, 调制控制二维非对称耦合环形腔光折变振荡器系统的时空混沌. 环形腔光折变振荡系统的动力学方程为
其中:f[In(i,j)]为局域动力学函数;εm(m=1,2,3,4)为空间相邻格点间的非对称耦合系数;
为环形腔激光器输出的混沌激光光强[4],α1为环形腔激光器的增益系数,Γ为环形腔激光器的腔损耗.
系统参数为式(8)-(9)及Ωτ=1.4,Γ=11.0, 初始条件为I0(i,j)=0.3,X0(i,j)=0.3, 边界条件为式(10), 从n=600步开始加入控制, 结果如图5所示, 其中: (A),(C)分别为α1=11.75,12.5时系统输出光强度随时间的变化; (B),(D)分别为α1=11.75,12.5时系统输出光强度的时空分布. 由图5可见: 当环形腔激光器增益参数分别为α1=11.75,12.5时, 系统分别被控制到周期4,2; 系统中每个格点输出的光强度不随时间变化, 但不同格点输出的光强度不同. 数值模拟结果表明, 混沌光场调制不能将二维非对称耦合环形腔光折变振荡器系统的时空混沌控制到周期1.
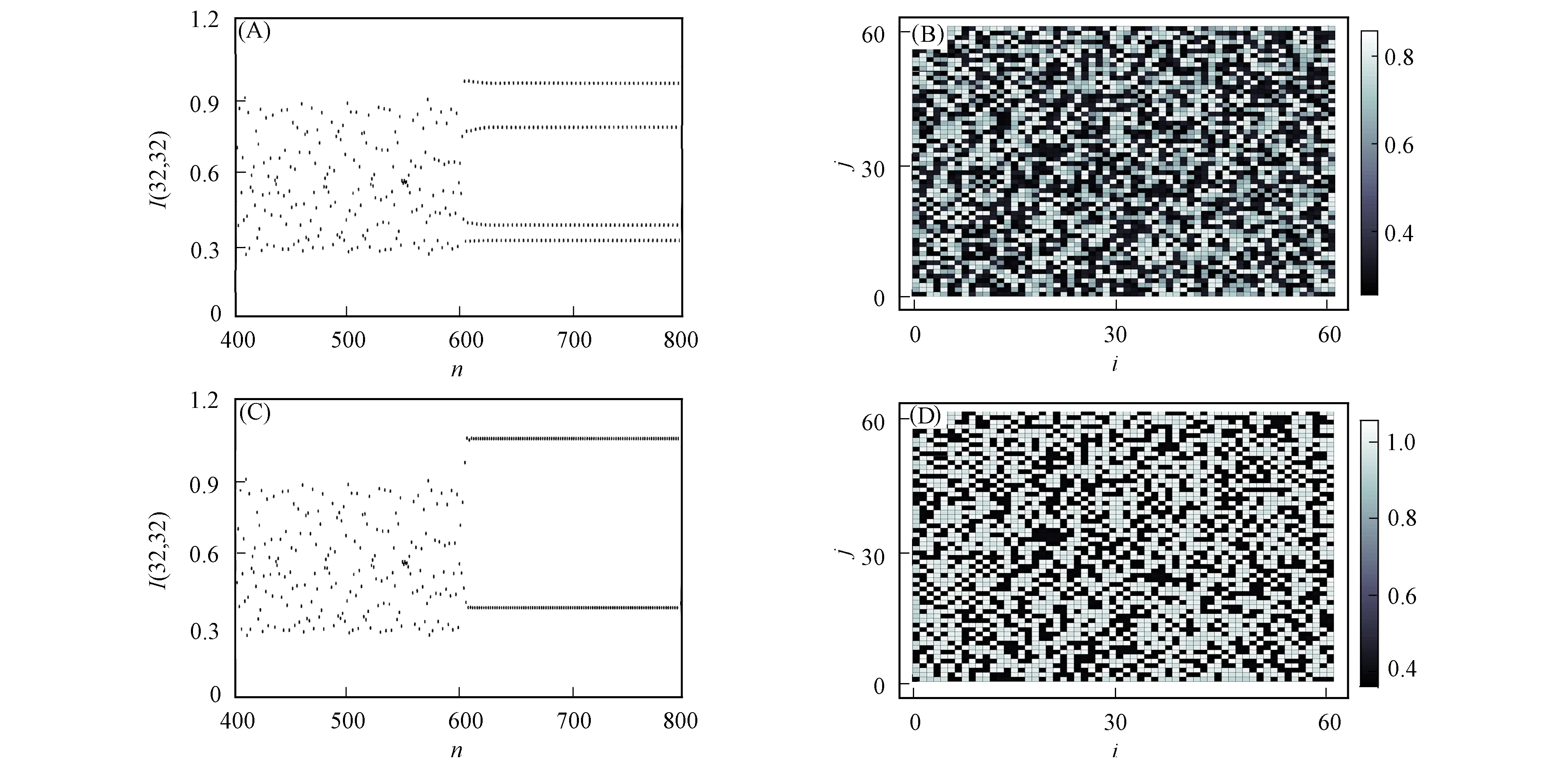
图5 混沌光场调制环形腔光折变振荡器二维时空混沌的控制结果Fig.5 Control results of two-dimensional spatiotemporal chaos by chaotic light field modulation in photorefractive ring oscillator
综上, 本文数值模拟了非对称耦合环形腔光折变振荡器的时空演化行为. 结果表明: 当边界条件、 初始条件以及系统参数取确定值时, 系统的输出状态随时间演化逐渐扩散到时空混沌状态; 当调制强度逐渐增加时, 处于时空混沌状态的二维非对称耦合环形腔光折变振荡器系统逐渐被控制到周期4、 周期2, 最后到稳定的周期1状态; 随着环形腔激光器输出激光光强参数的增大, 二维非对称耦合环形腔光折变振荡器系统从混沌状态逐渐被控制到周期4、 周期2状态, 系统受控后所处周期状态与参数变化导致的周期状态输出光强度不同.

