基于相似度投票的社区划分改进算法
冯成强, 左万利, 王 英
(吉林大学 计算机科学与技术学院, 长春 130012)
随着科技的发展, 出现了很多大型系统, 如果将这些系统的对象视为节点, 对象之间的关系视为边, 则这些系统将构成社会网络. 如电话通信网络、 WWW网络[1]、 社交网络用户关系网、 科学家合作关系网络[2]、 全球的Internet网等, 研究这些网络的特性将有助于发掘网络中隐藏的有用信息. 常见的社会网络特性有小世界性、 无标度性和社区结构性[3]. 社区划分是目前社会网络分析的研究热点. 社区划分就是找出社会网络中的某种内在结构, 使社会网络分裂成一个个的社区, 社区结构的定义如下: 社区结构是一些社区内成员关系密切联系, 社区间的成员关系稀疏的节点集合[4]. 近年来对社会网络划分的研究已取得了很多成果, 主要分为4类: 基于谱分割思想的方法[5]、 基于优化思想的方法[6-7]、 基于模块度的方法[8]以及基于相似度的划分算法. 基于模块度的方法一般属于层次聚类算法, 又分为凝聚式与分裂式两类, 均使用模块度作为社区划分准确率的评判标准. 文献[4]提出了第一个基于模块度的社区划分算法, 称为GN算法, 该算法通过不断删除边介数最大的边增大模块度, 直到模块度不再增加为止, 从而实现对网络的社区划分, 是一种分裂式的层次聚类算法; Newman[9]提出了一种凝聚型的层次聚类算法----FN算法, 该算法通过不断合并使模块度增加最大的两个社区对网络节点进行聚类, 最后达到划分的目的. 但以上两种算法对于大规模的社会网络在时间效率上存在明显缺陷, 为实现对大规模社会网络进行快速划分的目的, Blondel等[10]提出了Louvain算法, 该算法相对于GN算法和FN算法具有运行速度较快、 划分效果较好等优点. Louvain算法通过不断地将节点在其邻接社区中移除与并入来划分社区, 每次移动均需要计算模块度增量, 对于大规模的稠密网络迭代次数一般较多, 收敛速度较慢. 基于相似度的划分算法有: 近邻传播AP算法[11]、 基于聚簇相似度的社区划分方法[12]以及通过相似性度量条件进行社区划分的方法[13]. 节点相似度的构造[14]一般分为基于节点局部信息的与基于网络拓扑结构的两类. 基于节点局部信息的相似度计算方式主要有3种[15], 分别是Jaccard公式、 余弦相似度公式及分母最小化公式, 而基于网络拓扑结构的方法主要原理是依据随机游走的思想[16]. 由文献[14]结果可见, 基于节点局部信息计算相似度, 速度较快, 且准确度也较高.
鉴于局部相似度的计算简单、 速度快等优点与Louvain算法底层划分存在重复开销, 本文针对大规模的稠密网络提出一种基于节点相似度投票的改进算法来改善Louvain算法的第一层划分, 然后再结合基于模块度的Louvain算法实现对社会网络的快速划分.
1 模块度与Louvain算法
1.1 模块度
模块度是通过比较社区内节点的紧密程度及社区间节点的稀疏程度与相同规模随机网络中的期望值得出的, 定义如下:
(1)
其中:Avu表示节点v到u的边的权重;Kv表示节点v的度;m表示边的权重之和;γ(v,u)表示当u=v时表达式取1, 否则取0;Cv表示节点v所在的社区. 所以整个Q值的定义是所有节点到其他节点的边分布与随机分配节点边的差的加权求和. 对式(1)进行化简可得
(2)
其中: ∑in表示社区C内边的权重之和; ∑tot表示连接到社区C内节点的边的权重之和. 式(2)表明模块度是各个社区的模块度之和, 可分别进行计算. 模块度的取值范围为[-1,1][17], 值越大, 社区划分就越合理. 模块度作为一种广泛使用的度量标准, 其划分结果相对可靠.
1.2 Louvain算法
1.2.1 模块度增量 Louvain算法中的模块度增量是指把一个孤立节点v合并到其邻接社区C时带来的模块度的增加量ΔQ, 计算公式为
(3)
其中: ∑in表示合并前社区C内边的权重之和; ∑tot表示合并前连接到社区C内点边的权重之和;Kv,in表示节点v到社区C中节点边的权重之和;λv表示连接到v的边的权重之和. 对式(3)进行化简, 得
(4)
1.2.2 Louvain算法思想 Louvain算法是基于模块度的贪婪式算法.
1) 通过不断地将节点从当前所在社区中移除成为一个单独节点, 再把这个节点重新分配到其某个邻接社区中, 使得与该社区合并所带来的模块度增量最大;
2) 依次对每个节点进行上述操作, 直到所有的节点都稳定在各自社区中或达到最大迭代次数;
3) 将每个社区合成一个超点, 社区间的连边合并为超点间的连边, 为超点增加一条自环边, 权重为超点所代表的社区内边的权重之和, 合并后即重构为一个更简单的社会网络, 第一层划分完毕;
4) 以此类推进行其他层次划分, 直到某一层划分前后总的模块度不再增加为止.
使用伪代码描述如下:
算法1Louvain算法.
输入: 社会网络G(V,E); 输出:G(V,E)的社区划分结果Partition.
1) 计算网络的模块度Q1;
2) 初始化网络G, 每个节点作为一个社区;
3) FORvIN RANGE(n): /*n为节点总数*/
4) 将v从原来的社区取出, 合并到使得ΔQ最大且ΔQ>0的邻接社区中;
5) END FOR
6) 重复步骤3), 直到在一次遍历中没有节点改变划分或达到最大迭代次数;
7) 计算新的模块度Q2;
8) 将社区划分结果存入Partition中, 重构网络G;
9) 重复步骤1), 直到Q1=Q2;
10) 返回Partition, 结束.
1.3 Louvain算法的缺陷
由Louvain算法的划分过程可见, 将一个节点v从其原来的社区中移除, 再并入到模块度增量最大的邻接社区中, 如果假设当v移除后, 其邻接社区数为m, 则再将其重新并入新的社区中要计算m次ΔQ, 然后选择ΔQ增加最大的社区进行合并. 在移除过程中, 如果一个节点的社区归属改变了, 则其他顶点都将从其原来的社区中移除, 然后再重新归入某个邻接社区中, 即使其社区划分没有改变也需进行计算, 由此带来的重复计算将导致大量开销. 特别是在每层划分的最后阶段, 可能只有一个节点的划分与上一次划分不同, 但其他节点也得重新进行一次划分, 这样其他节点都在进行无效计算, 该缺点在大规模的稠密网络上表现特别突出.
一个节点v的社区划分变动, 可能引起另一个节点u的社区划分变动, 而u的社区划分变动可能再次引起v的社区划分变动, 如此进入一个死循环, 对于大规模的稠密网络这种情况很容易出现. Louvain算法中通过设置最大迭代次数跳出死循环, 但最大迭代次数却不易确定, 过大引起无效计算, 过小影响划分效果, 这是Louvain算法的另一个缺陷.
2 改进算法
在Louvain算法的第一层划分中由于网络节点较多导致社区划分收敛慢, 每次迭代过程中均有很多无效计算. 因此, 本文提出一种基于相似度投票的改进算法, 以改善Louvain算法的底层划分, 并将划分后的网络与Louvain算法相结合, 进一步提升社区划分的模块度, 从而完成社区划分.
2.1 改进算法主要思想
基于相似度投票的社区划分算法是一种凝聚式的划分算法, 通过为网络中的每个节点选择最佳的合并社区不断扩大社区规模, 从而完成社区划分.
1) 采取合适的相似度计算方式计算网络中每对邻居节点的相似度;
2) 初始化网络中的每个节点为一个单独社区, 对网络中的每个节点v进行如下操作:
① 通过v与其邻居节点的相似度及邻居节点的划分情况, 为v选择最佳合并社区C;
② 将v所在社区中的所有节点(包括v)合并到社区C中;
3) 根据步骤2)划分结果重构网络;
4) 使用Louvain算法对重构网络进行更高层次的划分, 从而完成社区划分.
2.2 节点相似度计算
网络中的节点彼此之间通过边相连, 与一个节点相连的点称为其邻居节点. 一个节点在网络中的位置与其邻居节点紧密相关. 利用两个节点的邻居分布, 可计算两个节点的相关程度, 即节点相似度. 一个节点与邻居节点的共同邻居越多, 则与该邻居节点越相似. 本文对相似度的计算方式定义如下: 首先根据网络边集合的每条边(v,u), 分别计算节点v与u的邻居集合Sv与Su; 然后利用Jaccard的变形公式计算节点v与u的相似度:
Simvu=Ψ(Sv,Su)/|Sv∪Su|,
(5)
其中: | |表示集合取模运算; ∪表示集合的并运算;Ψ(Sv,Su)表示当Sv与Su交集不为空时取交集的模, 否则取1. 计算完每条边两个节点的相似度后, 即得到了节点与每个邻居的相似度, 然后将节点与邻居的相似度作为划分该节点的依据. 改进算法的实验结果证明了该节点相似度计算方法较准确.
2.3 最佳合并社区的选择与社区合并
在改进算法中通过为每个节点选择社区进行合并来不断增大社区规模, 从而达到社区划分的目的, 如何为节点v选择最佳的合并社区是改进算法的关键. 为节点v选择最佳合并社区时利用了节点v与邻居节点的相似度以及邻居节点的划分情况, 最佳社区选择与社区合并过程如下:
1) 利用网络拓扑结构计算节点v0的所有邻接社区. 此时邻接社区可能会因为社区划分的程度不同(已划分节点的数量)而出现不同情况, 如图1所示, 其中: (A)表示在划分v0时其邻居节点尚未划分, 每个邻居是节点v0的一个邻接社区; (B)表示有些邻居节点已经完成划分, 划分到一起的邻居节点形成一个邻接社区; (C)表示已经有邻居节点被划分到节点v0的初始单独社区中, 形成了一个新的社区C3, 此时将社区C3除v0外的点构成的社区视为一个邻接社区.
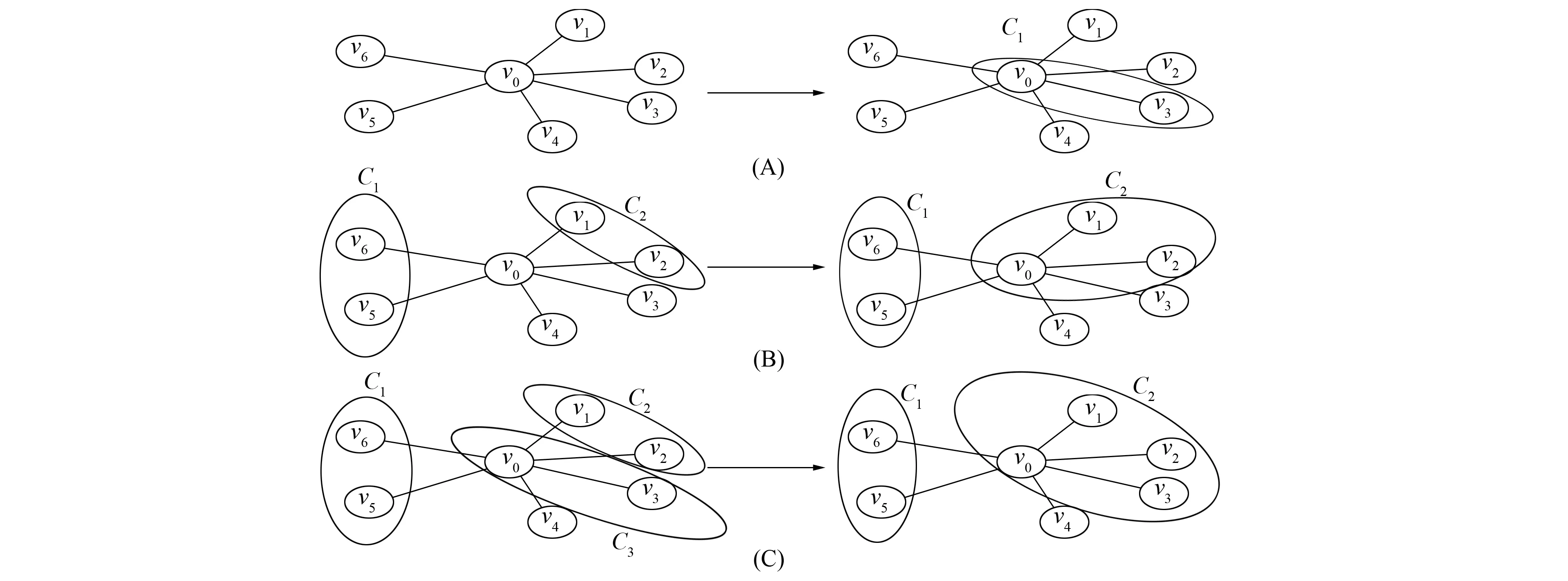
图1 不同情况下的节点划分示意图Fig.1 Schematic diagram of nodes partition under different circumstances
2) 利用相似度为每个邻接社区投票. 遍历v0的所有邻居节点, 先将每个邻居vi与v0的相似度作为票值投给vi所在的邻接社区, 再将同一邻接社区获得的票值累加, 形成投票积累, 如图1(B)中的邻接社区C2的得票即为v1与v0的相似度加上v2与v0的相似度, 其他类似.
3) 计算每个邻接社区的票值, 获得最大投票的邻接社区即为节点v0的最佳合并社区C.
4) 将节点v0或v0所属社区的所有节点合并到C中. 如图1所示, 其中: (A)表示将v0合并到与获得最高票值的邻居v3中, 形成社区C1; (B)表示将v0合并到获得最高投票的邻接社区C2中; (C)表示将v0所在社区中的所有节点v0与v3合并到C2中.
经过上述过程后,图1中的一个节点即完成了初步划分, 所有节点都经过处理后即完成改进算法描述中的步骤2).
开始阶段节点的每个邻居都是一个邻接社区, 相当于将节点代表的社区与最相似的邻居所代表的社区进行合并, 如图1(A)所示. 经过一部分节点划分后, 对于未划分的节点, 其节点的邻居可能已经完成了社区划分, 如图1(B)和(C)所示. 此时由于节点的一些邻居划分在同一个邻接社区, 对节点的邻接社区进行相似度投票将出现投票积累, 选择累积票值最高的社区进行合并, 而不是选择单个相似度最高的节点进行合并原因如下: 1) 通过累积获得最高相似度的邻接社区将有更多邻居节点与该节点相连, 将节点合并到这样的邻接社区中, 形成的社区更紧凑, 使得实验结果中改进算法社区数更少; 2) 该合并方式倾向合并出大的社区, 减少了小社区出现后又被合并的可能性, 从而减少了中间计算量.
2.4 改进算法的实现
为了更好地理解改进算法描述的社区划分过程, 下面将改进算法用算法2实现如下.
算法2改进算法.
输入: 社会网络G(V,E); 输出:G(V,E)的社区划分结果Partition.
1) 计算邻居节点的相似度Sim; /*结果以字典形式保存在Sim中*/
2) 初始化Community[v]=v,cMember[v]=[v]; /*初始化每个节点为单独社区并记录成员*/
3) FORvIN RANGE(n): /*v为网络中的一个节点,n为节点总数目*/
4)C=choseBestCommunity(v,G,Sim,Community) /*为v选择最佳合并的邻接社区C*/
5) IFv!=C: /*当选择合并的社区不为自身所在社区时, 才进行合并*/
6) FORkINcMenber[v]: /*将v所在的社区与邻接社区C合并*/
7)cMember[C].append(k); /*将v所在社区的成员加入社区C/
8) Community[k]=C; /*改变v所在社区成员的社区划分*/
9) END FOR
10) END IF
11) END FOR
12) 将Community存入Partition1中, 作为第一层的划分结果;
13) 将社区合并为超点, 重构网络G;
14) 调用算法1对网络G进行进一步划分, 结果保存在Partion2中;
15) 合并Partion1与Parttion2为Partition;
16) 返回Partition, 结束.
函数choseBestComunity为根据相似度投票为v代表的社区选择合并的邻接社区C, 实现步骤如下.
函数1choseBestCommunity.
输入: 节点v, 网络G, 相似度Sim, 当前社区划分Community; 输出: 节点v应合并的邻接社区C.
1) 声明字典neighborCom={ }; /*用于记录v每个邻接社区获得的票数*/
2) 根据网络G计算节点v的邻居列表neighborList;
3) FORuIN neighborList: /*根据v的邻居划分情况计算v的所有邻接社区, 初始票值为0*/
4) neighborCom[Community[u]]=0.0;
5) END FOR
6) FORuIN neighborList:
7) sim=Sim(v,u); /*读取v与u的相似度*/
8) neighborCom[Community[u]]+=sim; /*为包含u的邻接社区累积投票, 票值为sim*/
9) END FOR
10)C=neighborCom中有最大投票数的邻接社区; /*若最大投票有多个, 则任意选取一个社区*/
11) 返回邻接社区C, 结束.
算法2的步骤1)~13)是本文提出的改进算法部分, 其余部分则是直接运用Louvain算法, 所以二者的差距只在第一层的划分上. 改进算法在进行社团合并的过程中利用了节点的邻居划分情况, 以保证节点选择社区进行合并的合理性, 从而省去了模块度增量计算. 整个过程只需遍历所有节点一次即可完成初步社区划分, 相比Louvain算法的多次迭代要快很多.
2.5 算法时间复杂度对比分析
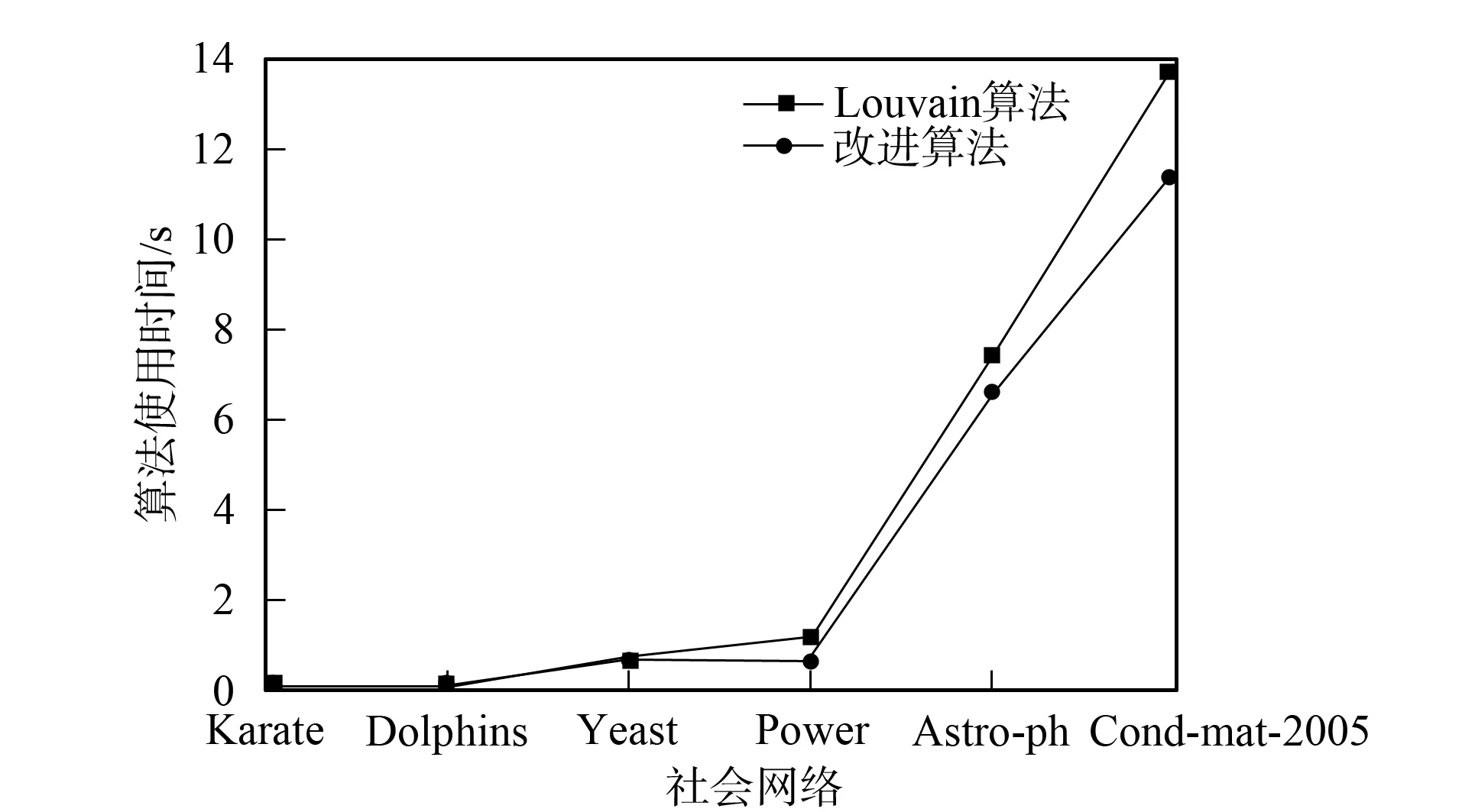
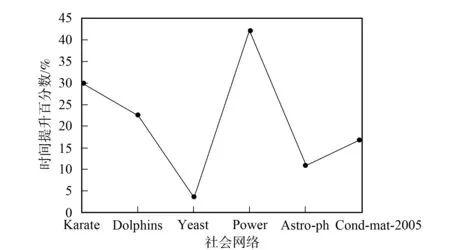
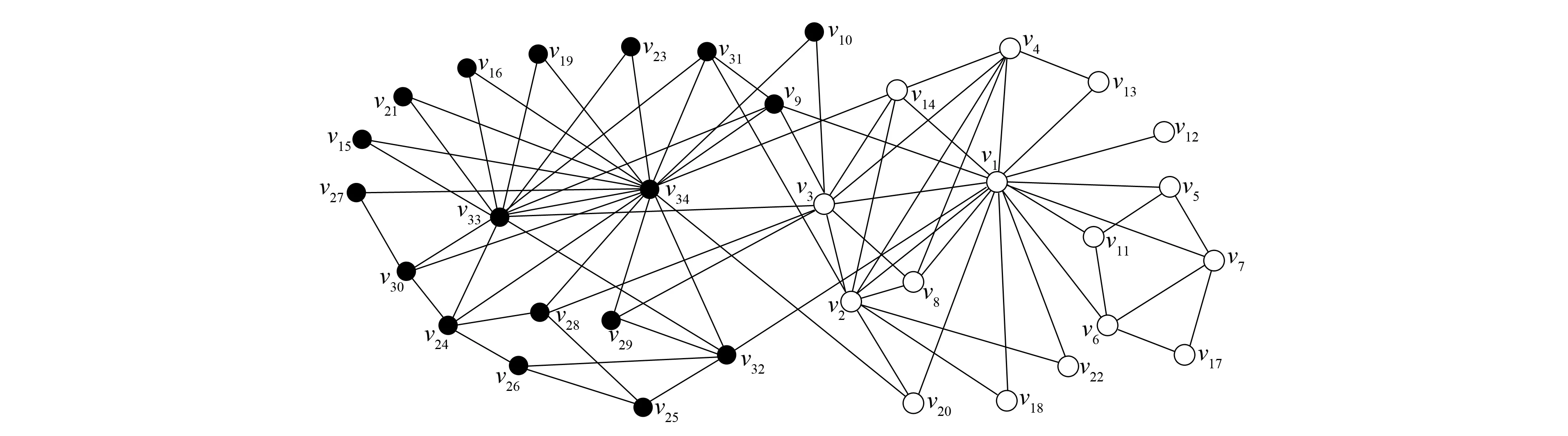
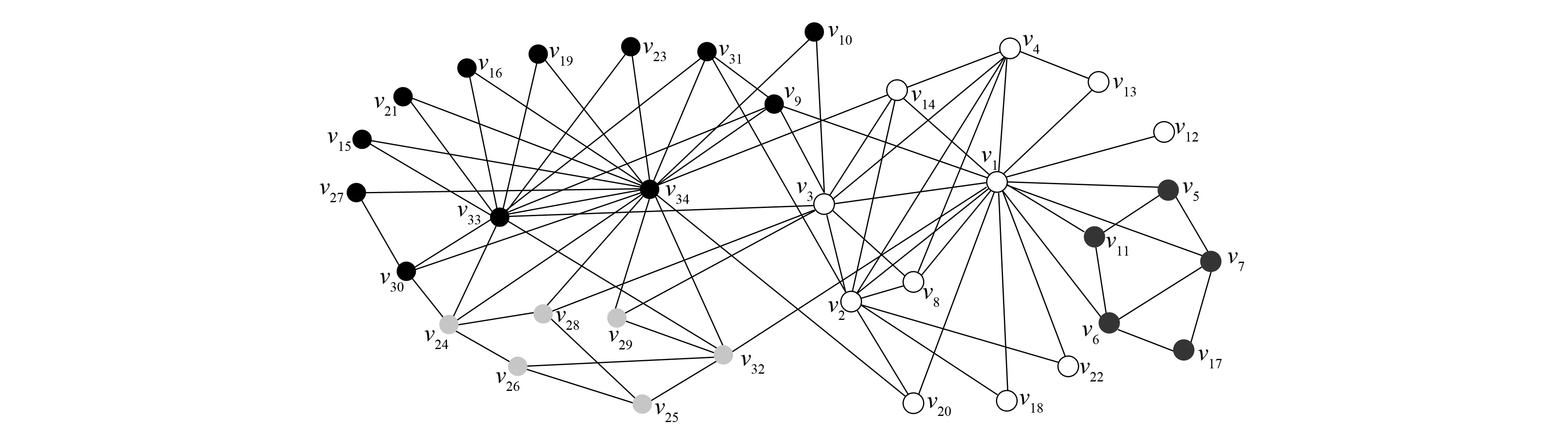
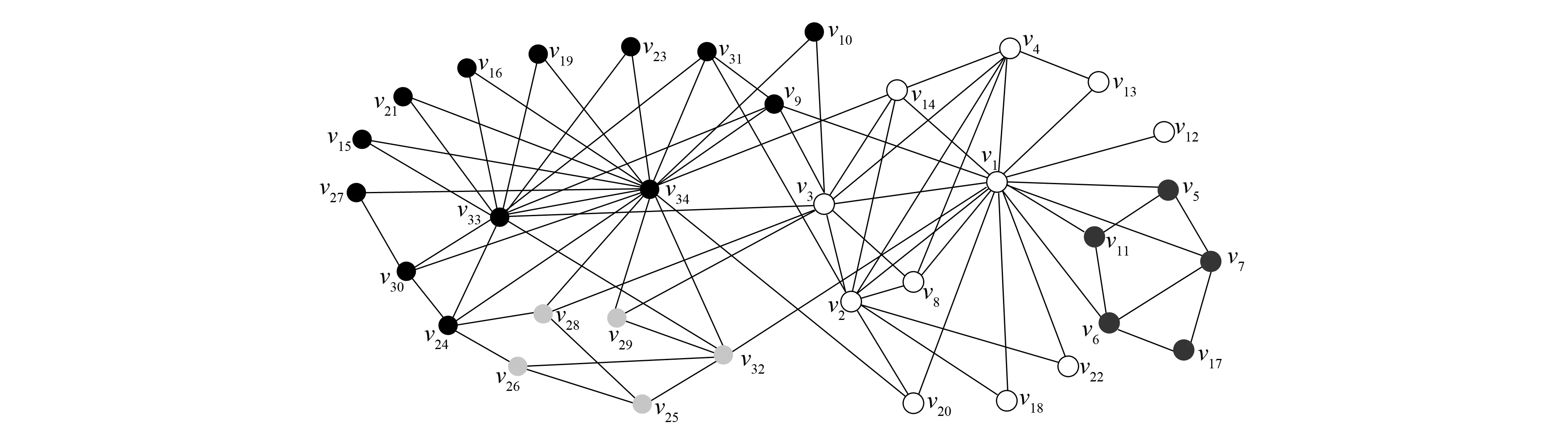
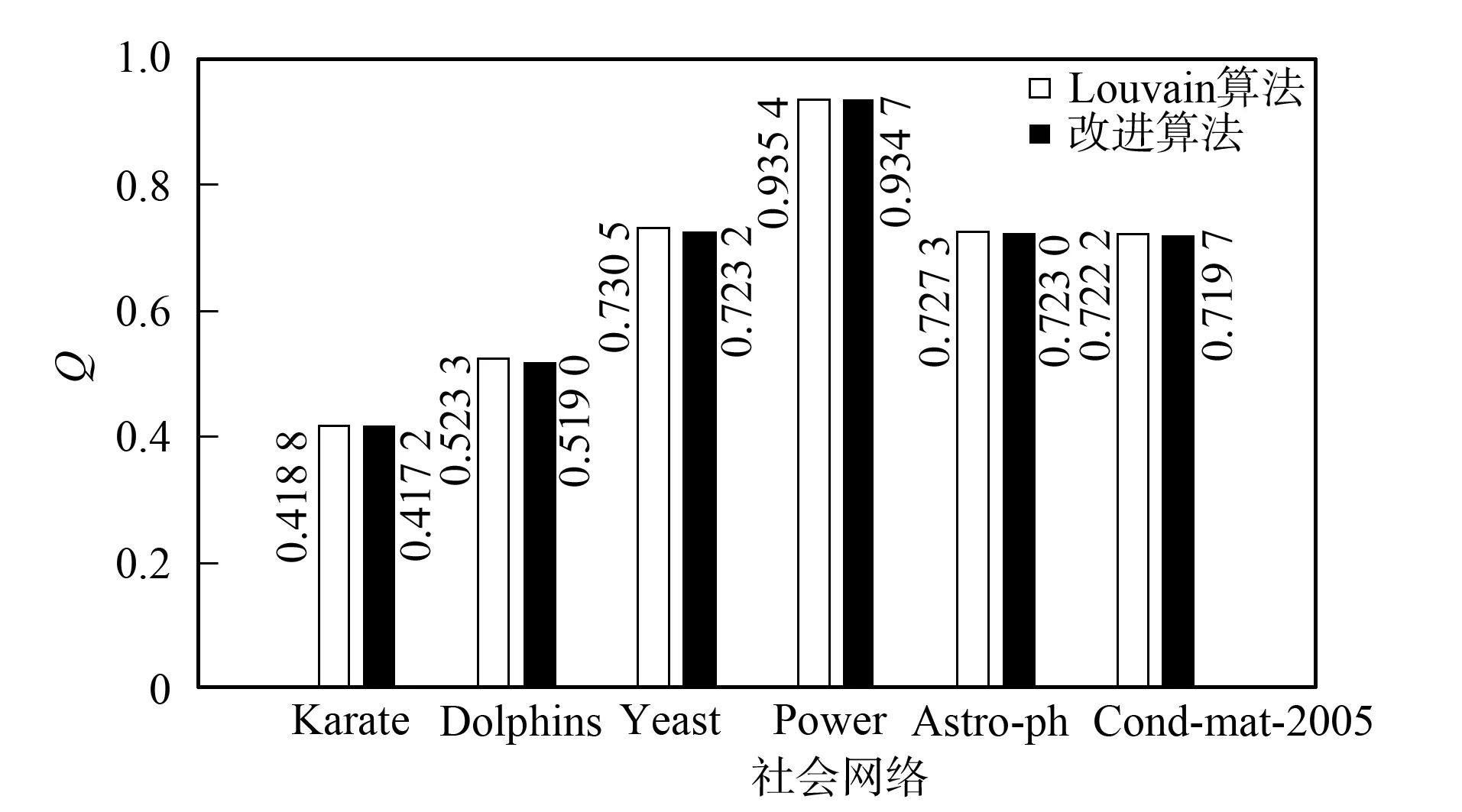
改进算法第一层划分的时间开销主要集中在节点的相似度计算及节点划分中的社区选择与合并两部分. 第一部分的时间复杂度为O(c1|E|), 其中:E表示社会网络的边集合;c1表示每对节点相似度计算的开销. 第二部分的时间复杂度为O(c2|V|), 其中:V表示顶点集合;c2表示为每个节点选择社区与进行社区合并的开销. 总的复杂度为O(|E|+|V|), 所以具有线性的时间复杂度. Louvain算法的第一层划分过程中遍历节点一次需要O(c3|V|)的时间复杂度, 其中c3表示移动一个节点的开销, 需要多次遍历直至节点划分不再变化, 设次数为γ, 则其时间开销为O(γ|V|), 所以当γ较大时, 其时间开销可能大于改进算法. 由于其他层次的划分采用相同的算法, 所以其时间复杂度相同, 且均为线性的. 将改进算法与Louvain算法第一层划分所用的时间分别记为T11和T21, 第一层后的划分所用时间分别记为T12和T22. 如果T11+T12 下面通过对改进算法与Louvain算法在真实数据上的实验结果进行比较与分析, 说明算法的有效性. 实验中采用的社会网络分别是Zachary空手道俱乐部成员关系网络[18]Karate、 海豚协作关系网Dolphins、 酵母遗传网络Yeast、 美国西部电力网络Power及两个规模更大的社会网络: 物理学家合作网络Astro-ph和Condensed matter collaborations网络Cond-mat-2005. 上述6个社会网络在规模上呈按节点数递增的关系, 表1列出了上述各网络的基本参数. 表1 社会网络参数 为对比改进算法在实际社会网络上的社区划分效果, 选用较经典的Zachary空手道俱乐部网络的划分结果对两种算法的社会网络划分差异做比较. Zachary是用于社区划分分析的经典社会网络, 包含34个点, 代表俱乐部的成员, 78条边代表成员之间的社会关系. 俱乐部因为是否提高收费产生争执, 分为2个真实关系社区. 如图2所示, 分别以节点v1为代表的白色社区1和以节点v33为代表的黑色社区2. 图2 Zachary关系网络Fig.2 Relational network of Zachary Louvain算法对未划分的Karate网络的划分结果如图3所示, 相对原始网络新增了3和4两个较小的社区, 整个网络被划分成4个社区: 白色的社区1, 黑色的社区2, 深灰色的社区3, 浅灰色的社区4. 改进算法对未划分的Karate网络的划分结果如图4所示, 同样划分4个社区, 相比Louvain算法划分的社区结构只有节点v24不同, 它从社区4移入到了社区2, 分析节点v24可知它与社区2中的度数较大的节点v33, 节点v34均直接相连, 所以将它划分到社区2更合理. 对比图3和图4可见, 改进算法在社区划分结构方面与Louvain算法相差较小. 图3 Louvain算法对Zachary的社区划分结果Fig.3 Community partition results of Zachary by Louvain algorithm 图4 改进算法对Zachary的社区划分结果Fig.4 Community partition results of Zachary by improved algorithm 图5 两种算法模块度比较Fig.5 Modularity comparison of two algorithms 根据6个社会网络的实验结果对Louvain算法与改进算法关于模块度与社区数目做出分析. 模块度Q作为社区划分算法效果的度量标准, 一般模块度越高, 社区结构划分越合理. 由文献[11]可见, Louvain算法相对于其他算法模块度相对较高.图5为Louvain算法与改进算法的模块度柱状图比较. 由图5可见, 改进算法与Louvain算法在模块度上的差别较小, 只略低于原始算法. 其原因可能是由于算法开始阶段, 对于处于划分后社区边界的节点由于其邻居节点尚未划分, 无法进行相似度投票而导致误划分. 纯模块度的度量标准倾向于小社区, 具有极端退化的现象[19], 所以可能导致Louvain算法的社区结构与实际社区结构不同, 但模块度却很高; 而改进算法则倾向于更紧凑的社区结构, 可能会有一小部分的模块度损失, 从而导致模块度略低于Louvain算法. 社区数目G也是用于测评算法准确性的一个重要度量标准. 合理的社区数目将使划分出来的社区结构更紧凑, 社区成员间的关系更符合实际情况. 表2列出了两种算法对6个社会网络划分的社区数目. 由表2可见, 改进算法与Louvain算法在前4个网络上划分的社区数目相差较小, 但均少于Louvain算法划分的社区数目; 后2个网络中, 改进算法相对于Louvain算法对大规模社会网络划分的社区数目更少. 表2 两种算法划分的社区数目比较 表3 FN算法与改进算法比较 准确性与时间效率是衡量算法优劣的两个重要指标.图6与图7分别是两种算法的时间开销(T)对比与时间提升百分数(1-改进算法时间/Louvain算法时间)对比结果. 由图6可见, 在6个社会网络中改进算法的时间开销均较小. 图7为改进算法对于Louvain算法的时间提升百分数. 由图7可见, 6个网络的时间提升百分数分别为30.0%,22.4%,3.6%,42.1%,11.0%,16.9%. 因此在前4个规模较小的社会网络上, 其中3个网络中改进算法的提升效果在20%以上, 在Yeast网络上只有3.6%. 分析Yeast网络可知其节点数很少, 却有近万条边, 在计算节点相似度上花销较大, 且节点少会加快Louvain算法的收敛速度, 所以提升效果不明显. 在Astro-ph和Cond-mat-2005大规模社会网络上提升的效率都超过了10%, 所以大规模网络的提升效果较明显. 改进算法在大部分的社会网络上的时间开销比Louvain算法少, 将改进算法用于大规模社会网络的社区划分在时间效率上可行. 图6 两种算法的时间对比Fig.6 Time comparison of two algorithms 图7 改进算法相对Louvain算法的时间提升百分数Fig.7 Time lifting percentage of improved algorithm relative to Louvain algorithm 综上可见, 本文从模块度、 社区数和时间效率三方面综合分析总结了两种算法在社区划分上的差异, 说明了改进算法用于社区划分的可行性. 对于一些基于社区划分的应用, 如果其对准确性要求不高, 则使用改进算法能更快地对用户的请求做出回应, 从而提升用户的体验效果. 对于需要实时划分的动态网络, 由于改进算法的节点相似度计算结果可重复利用, 只需重新计算由于节点变动带来的相似度变化的节点, 省去了大部分节点的相似度计算, 所以能很快地完成动态网络的社区划分.3 实验结果与分析

3.1 改进算法在真实社会网络上的社区划分
3.2 改进算法的模块度与社区数分析
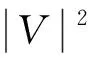


3.3 改进算法的时间效率分析