基于LabVIEW的时域积分的加速度信号的处理

王兴明，王成军

(1.安徽理工大学 机械工程学院，安徽淮南232001；2.安徽理工大学矿业工程博士后流动站，安徽淮南232001)

1 引言

铸造水平的高低能衡量一个国家的工业水平[1]。经实验研究发现，振动的幅度和频率会对铸件的性能和质量产生显著影响。振幅的大小及振动频率的高低对铸件的影响规律研究需要通过实验装置进行实时测量、分析，因此，需要开发专用的多维振动测试系统，对多维振动铸造机的振动参数进行测试、分析，为多维振动铸造机的产品开发和多维振动铸造工艺设计提供参考。

2 编程语言

LabVIEW(Laboratory Virtual Instrument Engineering Workbench)是由美国NI公司(National Instruments，国家仪器公司)开发出的一款功能强大且易于编程的仪器和分析软件，编程语言为G语言（图形化编程语言）。

3 测试对象

测试的对象是安徽理工大学自主开发研制的具有三个运动自由度的多维振动铸造机，其激振机构采用一种完全解耦的混联机构2PRRR—P（2R），能够实现砂箱沿X、Y、Z三个方向进行直线往复运动。振动铸造机的振动频率和振动幅度与负载密切相关，为了更直观地观测砂箱在各方向上位移的大小，采取空载测试方式，优选Z轴方向。

4 测试条件

采用的是压电式晶体三轴加速度传感器测量；采用归一化电荷放大器，且自带低通滤波器；采集卡为NI USB-6242，采集信号为模拟电压信号。由于实际的采样振动加速度信号，在去直流信号后仍存在偏差，因此对加速度信号积分后会产生趋势项[2]。

5 信号处理

加速度求位移，常用的处理方法有频域分析法和时域分析法两种。对加速度信号直接在时域上进行积分可可避免傅里叶变换引起的截断误差。

设采集到的加速度信号为α（t），加速度信号由积分性质可得

同理可得位移信号

其中：v′（t）是 v（t）的原函数，v0为初始速度；s′（t）为 s（t）的原函数，s0为初始位移。

在实际采样过程中，传感器获得的加速度信号含有直流分量，即 α（t）=α′（t）+δ，对含有直流分量的积分，式(1)和式(2)会有：

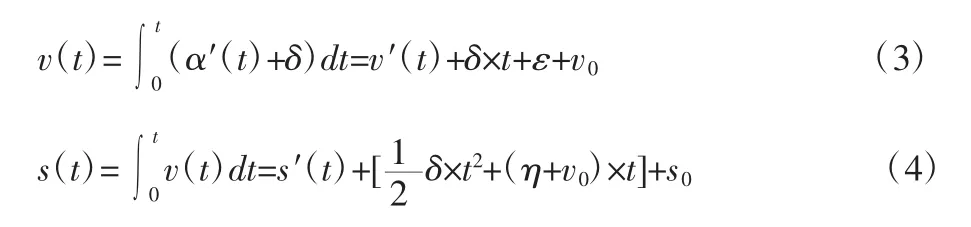
式（3）中ε和(4)式中η分别是加速度信号直流分量的一次积分（一次趋势项）和二次积分（二次趋势项）后产生的积分常量。如果不消除这些趋势向，误差就会越来越大。通常会用拟合多项式来消除趋势项，从而消除积分后产生的误差。

拟合多项式极值消除趋势。通过数值积分得到数据点（tivi）（i=0，1，...，n-1）。设

式中：pk为多项式系数，Ø为所有次数不超过m（m≤n-1）的多项式构成的函数类，使得式中：

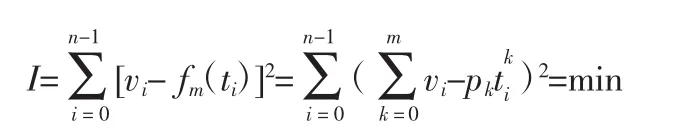
当某一组pk的值使I最小时，就可确定拟合趋势项。由多元函数求极值的必要条件，用矩阵表示

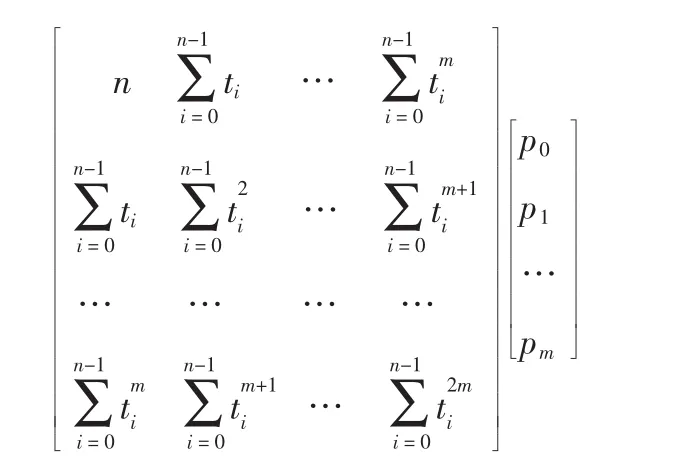
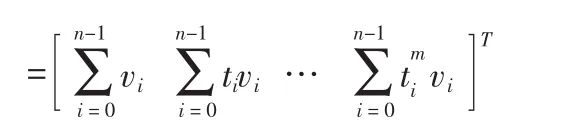
由解方程组可得

得到拟合趋势项f1（t）=p1t+p0。从而可以消除v0中的一次趋势项，同理，s（t）中含有二次趋势项，拟合多项式可消除 s（t）中的二次趋势项。

6 加速度信号处理程序

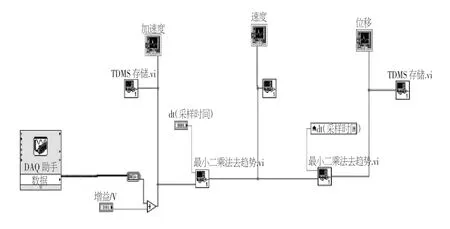
图1 加速度信号处理总程序框图

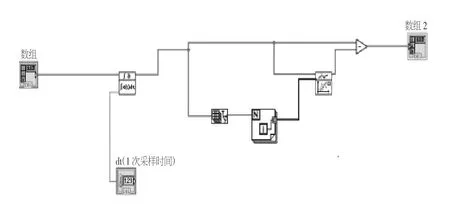
图2 拟合多项式程序框图

7 结论

本文利用压电式加速度传感器、信号调理设备、数据采集卡、PC机组成测量振动位移信号的硬件系统，采用图形化编程软件LabVIEW开发数据采集程序及基于拟合多项式极值消除趋势算法程序。在多维振动铸造机试验台上完成了实际振动位移测量。结果证明了该方法可以有效地将振动加速度信号变换成振动位移信号，很好地抑制了积分过程中趋势项的影响，能够达到实际振动测试的任务要求。