非线性渗流对特低渗油藏数值模拟开采的影响

姜瑞忠 张福蕾 崔永正 张海涛

中国石油大学(华东)石油工程学院, 山东 青岛 266580

0 前言

自1990年以来,特低渗油藏在我国能源结构中的地位越发重要,特低渗油藏的渗流机理和渗流模型的应用性很强,但对两者的研究是基础性的。渗流机理[1-8]、规律[9-14]和模型[15-17]以及关于特低渗油藏的数值模拟技术[18-21]都是科研人员的关注点。然而特低渗油藏渗流曲线的非线性段对油藏开发动态的作用仍未被商业化软件所考虑。同时比较成熟的数值模拟软件的基础主要是拟启动压力梯度模型,非线性段的影响未得到重视,由此得到的模拟结果存在较大的偏差。

本文调研了国内外已有特低渗油藏储层物性、非线性渗流理论和数值模拟技术的成果,在此基础上建立了特低渗油藏非线性渗流数值模型。用自制软件模拟非线性渗流对特低渗油藏数值模拟开采的影响,比较了达西模型、拟启动压力梯度模型和非线性模型的差异,对方向性、油水相态等进行了敏感性分析。

1 数学模型的建立及求解

渗流方程采用杨清立等人提出的两参数连续模型[17],该模型可以很好地表示非线性段,其模型如下所示:

(1)

式中:b为拟启动压力梯度的倒数,(MPa/m)-1;a是非线性凹形曲线段的影响因子。

油气水三相的运动方程为:

(2)

将运动方程代入连续性方程中,得到特低渗油藏渗流数学模型为:

(3)

(4)

(5)

初始条件:

pwt=0=pwi(x,y,z)

(6)

Swt=0=Swi(x,y,z)

(7)

Sot=0=Soi(x,y,z)

(8)

外边界条件:

(9)

内边界条件:生产井的井底流压或产液量恒定,注水井的井底流压或注入量恒定。

式中:qov、qwv、qgv为单位时间注入量或采出量,cm3/s;So、Sw、Sg为饱和度,ψo、ψw、ψg为三相的势,atm;ρo、ρw、ρg为密度,g/cm3;Bo、Bw、Bg为体积系数;μo、μw、μg为黏度,mPa·s;Rso、Rsw为溶解气油比,cm3/cm3。

依据块中心七点有限差分法建立全隐式数值模型对上述所建立的数学模型进行求解。

2 非线性渗流的影响

建立数值模型,网格数Nx=Ny=93、Nz=5,空间步长Dx=Dy=Dz=5 m,渗透率Px=Py=Pz=10×10-3μm2;孔隙度是0.25;四注一采,五点井网;定产量7 m2/d弹性开发10 a后转注水开发,注水阶段定产量18 m2/d,继续开采10 a。考虑不同非线性渗流情况进行模拟开采，对开采20 a的结果进行分析讨论。

2.1 非线性流与线性流的对比

图1为不同模型的剩余油饱和度模拟图,可以看出,达西模型、拟启动压力梯度模型、非线性模型(a=0.5)、非线性模型(a=1)的剩余油饱和度分布存在明显的差异。达西模型的开采效果最好,油藏各个部位的油都有采出;拟启动压力梯度模型的水驱方向主要沿水井到油井的垂直方向,水平方向波及效果较达西模型差得多,剩余油分布的形状以油井为中心形成明显的“十”字形;随a值的减小,非线性模型剩余油的分布形态越来越接近拟启动压力梯度模型的形态。这是因为非线性模型a值越小,启动压力梯度越大,泄油区域边缘处的流体不能流动,缩小了有效泄油面积。

图2为不同模型的日产油量对比曲线,达西模型的日产油量最高,拟启动压力梯度模型最低,非线性模型介于两者之间;图3为不同模型的生产井井底流压对比曲线,达西模型生产井的井底流压最大,拟启动压力梯度模型最低,非线性模型介于两者之间;图4为不同模型的注水井井底流压对比曲线,注水井井底流压的模拟结果与生产井恰好相反,非线性渗流的注水井井底流压比达西模型高。从图2～4可知,拟启动压力梯度模型的生产效果最差,在一定程度上夸大了地层阻力。而达西模型没有考虑启动压力梯度的存在,减小了地层阻力对渗流的影响。非线性模型的模拟结果表明启动压力梯度的存在导致渗流阻力增大,增大了生产压差,降低了生产效果。

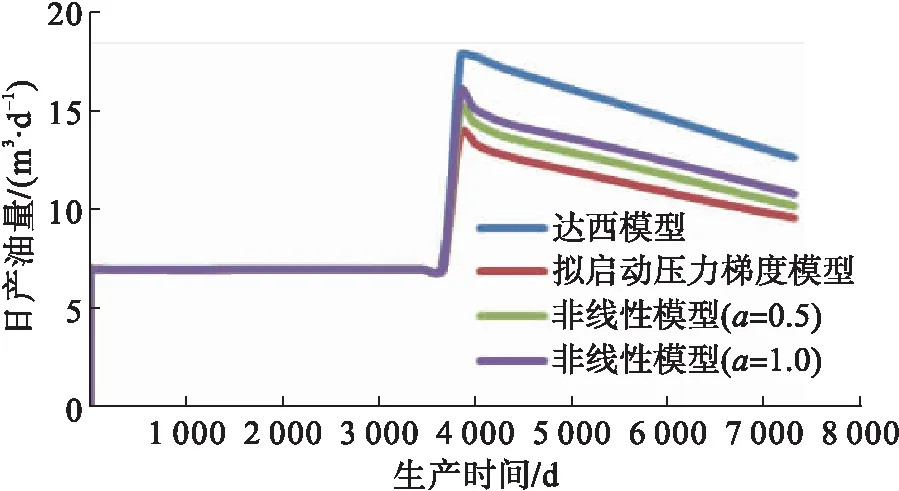
图2 不同模型的日产油量对比

图3 不同模型的生产井井底流压对比

图4 不同模型的注水井井底流压对比

2.2 方向性非线性分析

图5显示了不同方向非线性渗流时的剩余油饱和度模拟图,当不同方向非线性渗流时,含油饱和度的分布表现出明显的方向性。x方向为非线性渗流时,水驱方向向y方向偏离油水井的垂直方向,以生产井为中心的纵向的原油被明显地驱替出来;y方向为非线性渗流时,水驱方向向x方向偏离,以生产井为中心的横向的原油被明显地驱替出来;z方向为非线性渗流时,剩余油在水平面的分布是对称的。

图6显示了不同方向非线性渗流时的日产油量对比曲线,x方向和y方向非线性渗流时的日产油量是相同的,且明显低于z方向非线性渗流时的日产油量;图7显示了不同方向非线性渗流时的生产井井底流压对比曲线,z方向的生产井井底流压高于x方向和y方向;图8显示了不同方向非线性渗流时的注水井井底流压对比曲线,z方向的注水井井底流压低于x方向和y方向。从图6～8可知,x方向和y方向的非线性渗流在产油速度和生产压差方面的影响是一致的,相较于x方向和y方向的非线性渗流,z方向非线性渗流的影响较小,这是因为模型以水平方向的流动为主。

2.3 油水相态非线性分析

图9为不同相态的剩余油饱和度模拟图,油相非线性渗流时的含油饱和度分布与水相表现为非线性渗流时在各个阶段形状上有很大的不同。考虑油相非线性渗流时,剩余油分布以生产井为中心为明显的“十”字形,水驱波及区域大,但波及程度小;考虑水相非线性渗流时,开采效果较油相为非线性渗流时要好,剩余油分布的“十”字形发散,水驱波及区域较小,但采出程度较大。这是因为考虑油相非线性渗流时,水相渗流仍然符合达西定律,水沿油水井直线方向突进严重。

图6 不同方向非线性渗流的日产油量对比

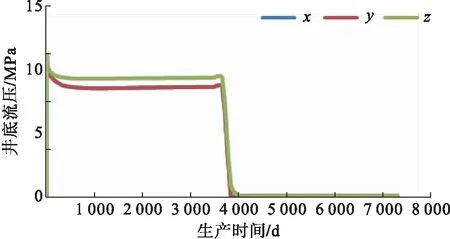
图7 不同方向非线性渗流的生产井井底流压对比

图8 不同方向非线性渗流的注水井井底流压对比

图10给出了不同相态的日产油量对比曲线,油相为非线性渗流时的日产油量比水相为非线性渗流时明显降低;图11给出了不同相态的生产井井底流压对比曲线,油相为非线性时的生产井井底流压偏低;图12给出了不同相态的注水井井底流压对比曲线,水相为非线性时的注水井的井底流压较低。从图10～12可知,仅考虑油相非线性渗流时,水相渗流阻力小,油井见水后,水的优势通道形成,采出程度降低;而考虑水相非线性渗流后,水的渗流阻力增大,油水流度比变小,采出程度增加。

图10 不同相态的日产油量对比

3 结论

1)本文以特低渗油藏非线性渗流数值模拟技术为主要的研究方向,建立了特低渗油藏非线性渗流数值模型。用自制软件模拟研究非线性渗流对特低渗油藏数值模拟开采的影响,比较了达西模型、拟启动压力梯度模型和非线性模型的差异,对方向性、油水相态等进行了敏感性分析。

2)拟启动压力梯度模型的水驱方向主要沿水井到油井的垂直方向,水平方向波及效果较达西模型差得多,剩余油分布的形状以油井为中心形成明显的“十”字形;随a值的减小,非线性模型剩余油的分布形态越来越接近拟启动压力梯度模型的形态。拟启动压力梯度模型的生产效果最差,在一定程度上夸大了地层阻力;达西模型没有考虑启动压力梯度的存在,减小了地层阻力对渗流的影响;非线性模型中启动压力梯度的存在导致渗流阻力增大,增大了生产压差,降低了生产效果。

3)x方向为非线性渗流时,水驱方向向y方向偏离,以生产井为中心的纵向的原油被明显地驱替出来,而y方向为非线性渗流时的情况恰好相反,z方向非线性渗流的影响较小,这是因为模型以水平方向流动为主。

4)考虑油相非线性渗流时,水驱波及区域大,但波及程度小,水相渗流阻力小,油井见水后,水的优势通道形成,采出程度降低;考虑水相非线性渗流时,开采效果较油相为非线性渗流时要好,水驱波及区域较小,但采出程度较大。