基于深度置信网络的农用地基准地价评估模型

王 华，罗 平，赵志刚，聂 可



基于深度置信网络的农用地基准地价评估模型

王 华1,2，罗 平1，赵志刚1，聂 可1

（1. 国土资源部城市土地资源监测与仿真重点试验室，深圳 518034；2. 郑州轻工业学院计算机与通信工程学院，郑州 450002）

该文针对现有基准地价评估模型主观性较强及精度不够等问题，提出了一种基于深度学习思想的农用地基准地价评估方法，构建了样本特征集合与地价标签集合的深层网络结构映射关系，并以广东省普宁市农用地基准地价评估为实例，验证了模型的可行性和有效性。结果如下：1）与神经网络、支持向量机这类浅层学习模型相比，深度置信网络模型其对地价的拟合精度要高出3.61%，3.12%；2）在训练样本只有300时，深度置信网络模型对地价的拟合误差为16.43%，比神经网络、支持向量机模型的拟合精度最少要高出6.76个百分点；3）深度置信网络模型对单个样本的运算时间及内存占用比神经网络、支持向量机模型都要高，但在评估精度都达到95%左右的情况下，深度置信网络模型所需训练样本较少，支持向量机训练时间为193 s，而深度置信网络模型耗时187 s，两者耗时基本持平；4）基于DBN模型对耕地评估单元的地价测算结果，将将普宁市耕地评估单元划分为5级，然后利用面积加权法求取对应的级别基准地价范围为21.34～26.23元/m2。上述试验结果表明该方法在对样本点地价的评估精度上要优于传统的浅层方法，并且该模型计算所得普宁市耕地基准地价与耕地质量在空间分布规律上保持一致。

土地利用；模型；农用地估价；深度学习；深度置信网络；基准地价；普宁市

0 引 言

农用地估价（agricultural land appraisal，ALA）工作是中国为促进农村土地使用制度深化改革而开展的一项重要工作，可为国家科学合理、依法统一管理农用土地、培育土地市场，提供科学精确的农用地标准价格体系[1]。农用地基准地价评估对于顺利开展土地承包经营权流转、征地补偿、土地整理、土地资产合理配置等农村土地管理工作具有十分重要的意义[2]。

中国在地价评估工作实践当中常用的方法包括算术平均模型[3]及回归模型[4-6]：算数平均模型对某均质区域内的样点地价取平均值来确定该区域基准地价，其缺陷在于该结果严重依赖于区域内样点的空间及数量分布情况；线性模型和指数模型等回归统计模型通过建立样点地价与土地级别或定级单元作用分值之间的数学模型来预测基准地价，但该模型需要预先人为确定众多影响因素权重值，具有很大的主观性、经验性与不确定性，并且无法准确地模拟地价与其影响因素之间复杂的非线性关系[7]。针对传统方法存在的缺陷，有研究人员尝试利用模糊数学[8-9]以及云模型[10]等方法来改进传统回归模型，但上述方法更为关注定性因素的评估量化，未改善回归模型的先天缺陷。由于影响地价的自然、社会、经济等因素在空间上均具有随机性和结构性，为消除变量本身的空间自相关对回归结果的影响，Kriging空间插值法[11-12]被用于构建地价求解方程，但该方法并未消除影响因素权重取值的随意性。近十几年来，人工神经网络模型在基准地价评估研究中获得广泛应用[13-16]。人工神经网络模型具有自主学习地价样本特征的优势，且不需要确定权重，克服了多因素权重确定受人为因素影响大的缺陷，并可利用多层神经网络建立地价与影响因素之间的映射关系。也有学者进一步提出基于支持向量机（support vector machine，SVM）的基准地价评估模型，该算法无论是对样本的拟合情况以及对地价的测算精度都要略优于人工神经网络模型[17]。无论是人工神经网络模型或者支持向量机都属于浅层学习算法，其有限的计算单元导致浅层学习的网络难以全面的表征影响因素与农用地基准地价之间的复杂函数关系，并且随着样本数量的浮动及多样性增加，浅层模型也无法适应复杂的样本[18]，地价评估精度也因此受到较大影响。

近些年兴起的深度学习技术由于拥有多层非线性映射网络层，使其具有强大的复杂函数表达能力，在复杂分类、识别、预测等问题的解决中获得了广泛应用，并取得良好的效果和效率[19-20]。深度学习可以看作为神经网络的发展，Hinton等[21]认为深层神经网络结构可以学习到对象更深刻更本质的特征。为解决上述问题，本文尝试选择深度学习的经典算法深度置信网络（deep belief network，DBN）[22]来构建农用地基准地价评估模型，并以广东省普宁市农用地基准地价评估为实例，对基于深度学习的农用地基准地价评估模型的原理及建立流程进行了探讨和研究。

1 基于深度学习的农用地基准地价评估模型

1.1 深度置信网络理论

深度学习是一类新兴的多层神经网络学习算法，通过多隐层感知器来组合低层特征形成更加抽象的高层表示，自动地学习得到层次化的特征表示，从而有助于提高分类和预测的准确性。DBN 结合了无监督学习和有监督学习，是由若干层无监督的受限玻尔兹曼机(RBM，restricted Boltz-Mann machine)和一层有监督的反向传播网络(BP，back-propagation)组成的一种深层神经网络（如图1所示），其基本思想是采用无监督学习方法逐层训练每一个RBM，最后对整个网络采用有监督学习进行微调。

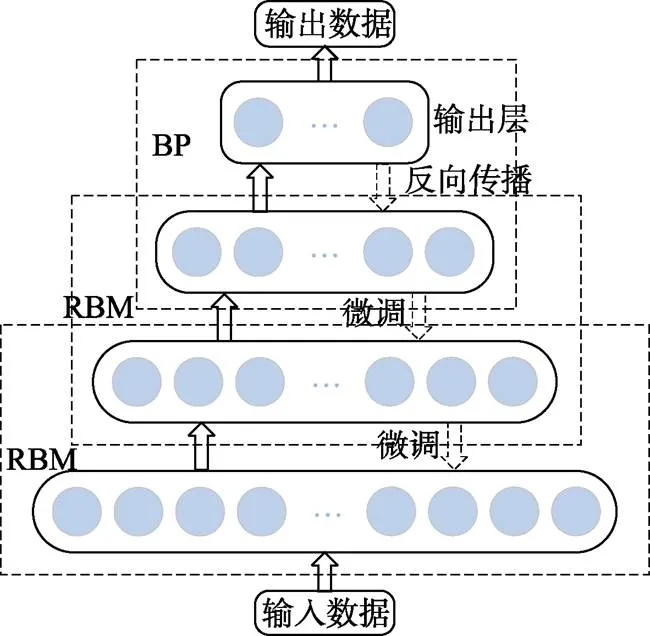
图1 DBN结构图

受限玻尔兹曼机（RBM）是一种特殊的玻尔兹曼机，由一个可视层（）和一个隐含层（）组成，可以看作为一个二部图，两层之间通过权重连接，同层单元之间没有连接（如图2所示）。可视层中任一可见节点v和隐含层中隐含节点h之间都存在一条权值为w的连接，且w=w，0<<，0<<。

图2 RBM示意图

RBM进行无监督学习的目的就是通过吉布斯抽样不断调节连接权值及偏置参数，最终使得隐含特征信号还原重建成¢后与之间误差最小。由于难以确定概率变化斜率计算的步长，Hinton[23]提出了一种对比散度（CD，contrastive divergence）算法来加速RBM训练过程并保持了精度。

1.2 深度置信网络地价评估模型

1.2.1 农用地基准地价评估问题描述

农用地基准地价受自然、经济、区位等多种因素影响，评估结果既能够表现出自然经济因素影响土地价值的区域空间结构性特征，也能反映人文活动及其它因素对地价的随机性扰动。农用地基准地价评估问题实质就是在对自然经济影响因素作用量化的基础之上，利用评估模型构建起地价与多维特征之间的复杂映射关系，基于该映射关系求取不同级别评估单元价格，进而确定均质区域内基准地价。

对于农用地基准地价评估问题，样本特征即为评估模型的输入，将样本特征数据集表示为

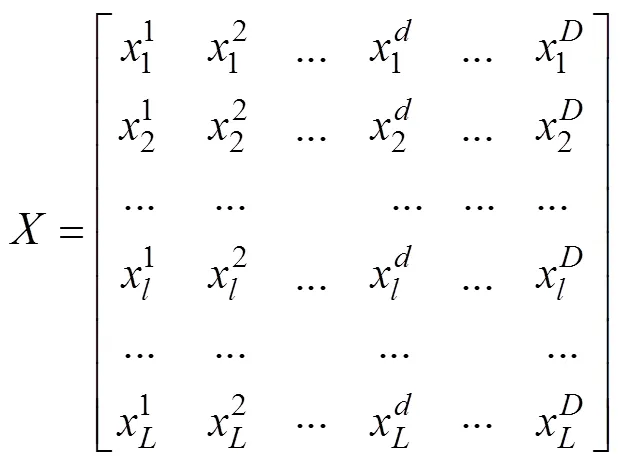
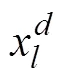
为与样本特征数据集对应的样本标签数据集，可以表示为式（2），y表示第个样本地块对应的实际市场价格。

农用地基准地价评估的核心即为寻找映射→的问题。由于特征维数较高，映射关系通常会非常复杂，通过机器学习方法，特别是深度学习方法能够对这类问题进行较为准确的求解。基于该映射网络可以将各级别评估单元的特征向量分别输入，通过DBN模型参数计算输出评估单元地价，再通过加权或者取平均值的方法即可求取某一级别的平均地价即基准地价。

1.2.2 模型的建立

选择如图1所示的DBN网络来建立农用地估价模型，它由输入层、多层RBM和BP微调层构成，输入层为土地价格影响因素x，输出层为评估地价y。农用地估价DBN模型的建立流程如图3所示。

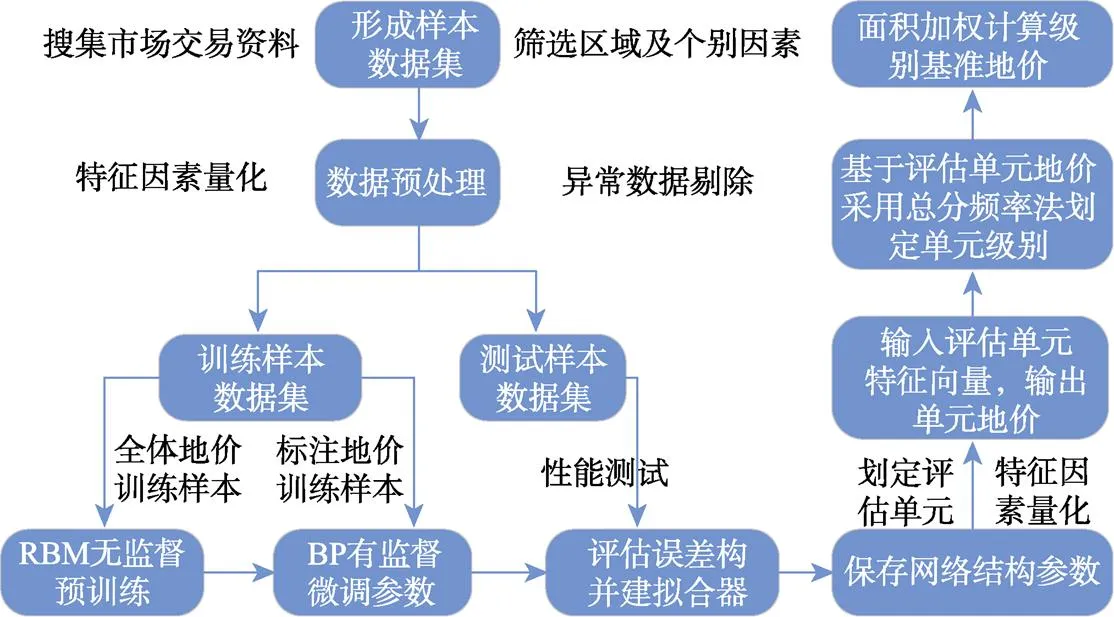
图3 农用地估价模型的构建

1)采用z-score方法对样本集特征数据及进行归一化预处理，如式（3）所示。其中为归一化后的数据特征值，为某一具体特征值，为平均数，为标准差。

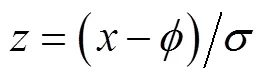
归一化的目的：一是为满足DBN算法对输入特征数据格式的要求；二是消除不同量纲的影响从而避免部分特征无法有效参与地价评估。

2)将原始样本集合按照设定比例随机拆分为训练样本集合（train，train）和测试样本集合（test，test），并给定所有样本的地价标签。

3)样本预训练：以全体训练样本数据集的维特征向量作为输入，地价向量为输出，采用逐层地无监督贪婪学习的方法来训练模型中的RBM。在每一层，可视层h及隐含层v单元的状态按照式（4）和式（5）进行计算，b表示可视层偏置量、c表示隐含层偏置量，参数空间（，，）可通过CD算法进行更新。

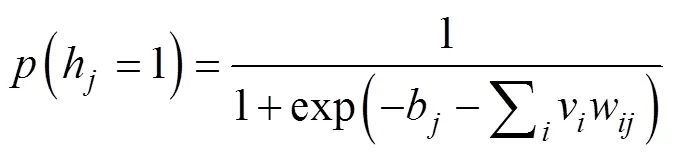
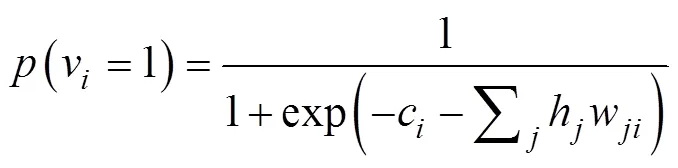
4)微调：采用有监督学习方式对最后一层的BP网络进行训练，具体是将最后一层RBM的输出由BP输入端传到输出端，然后根据前向传播的输出结果与预期值的误差从输出端到输入端进行反向传播，进而对整个DBN网络参数进行微调，直到迭代次数达到设定值为止。

5)测试及评估：将测试样本数据集输入到训练好的DBN，利用模型的输出地价与样本标签地价计算得到平均评估误差率λ（如式（6）所示）并将其作为衡量DBN 评估性能的标准，式中test表示测试样本的实际地价，test表示测试样本集合的数量，表示模型的输出地价。

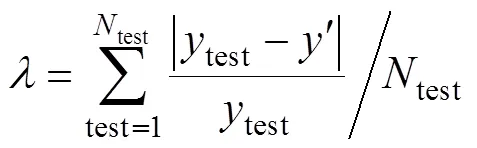
6)计算评估单元地价：对评估单元每一个特征值进行量化，并同样按照公式（3）进行归一化，并输入到训练好的DBN网络之中，可计算得到每一个评估单元的地价。

7)划定单元级别：采用总分频率法以所有评估单元输出地价作为依据划定评估单元级别，并用道路、地类界、权属界、其它线状地物校核级别边界。

8)计算基准地价：本模型选用面积加权法，利用每一级别内的评估单元的地价及对应的面积权重进行基准地价计算，如公式（7）所示：BValue表示第级别的基准地价，Area表示级别内第个评估单元的面积，TotalArea表示级别的所有单元的面积之和，ZValue表示利用模型求取的第个评估单元的地价。

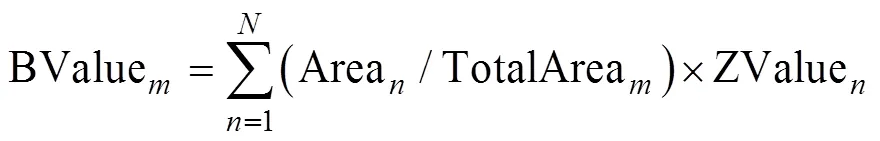
2 研究区及数据来源

2.1 研究区概况

普宁市位于广东省东部偏南，潮汕平原西部。东毗潮阳市，南临惠来县，西南连陆丰市、陆河县，北接揭西县，东北与榕城区交界。市域东西约50 km，南北约38 km。市区东至汕头市70 km，西距广州市约400 km，市域南部距海岸线30 km。行政区范围位于115°43¢10²～116°21¢02²E和23°05¢40²～23°31¢48²N之间（如图4所示）。全市总面积1 604.23 km2。全市设20个镇、5个街道办事处、3个国营农场；有519个村委会、48个居委会。区域面积1 620 km2，其中耕地2.58万hm²，占15.9%。

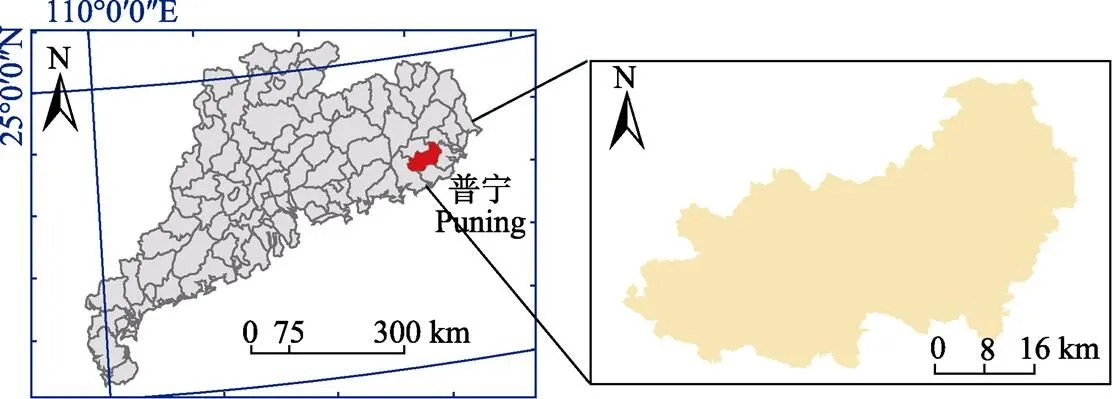
图4 普宁市区位图

本研究涉及到的数据主要包括土地利用、气候、水文、土壤、地形、交通条件、土地经济等方面的资料及空间图件等。土地利用数据来源于普宁市国土环境资源局提供的土地变更调查数据、土地利用更新调查和第二次土地调查数据库；地形坡度、灌溉保证率、pH值、有机质含量等数据同样来源于普宁市国土局提供的农用地分等定级数据；道路通达度、汽车站主要参考交通部门提供的道路等级图、道路分布图、交通图等资料。

2.2 农用地估价特征体系

普宁市农用地地价评估对象包括耕地、园地、林地、养殖水面4类用地单元，本文只以耕地单元评估为例。一般而言，影响农业用地地价的因素指标有: 地形地貌、土壤条件、水资源状况等自然因素；基础设施、土地利用状况、耕作便利条件等社会经济因素以及交通条件、区位条件等区位因素。根据农用地定级估价国家规程中推荐的因素体系，课题组在征求普宁市国土资源局、农业局、水利交通及从事土地定级估计的专业人士的意见基础之上，参考现有研究对于农用地地价影响因子的分析[5,12,24]，利用特尔菲法最终确定普宁市耕地价格评估因素体系，共计19个评价因子，如表1所示。

2.3 样本点集合构建

本课题组在全市范围内以调查表格的形式进行样点资料外业调查，同时使用手持GPS进行样本点定位，确保每一个行政村都至少包含十个以上的样点，共计12 555个水田和旱地投入产出样点。对每一个样点从种植收益、农用地出租、承包转包、土地开发、农用地抵押以及农用地征用等几个方面进行资料收集和调查工作（如表2所示）。对初步调查的样点的总收益（主产品产量´单价+副产品产量´单价），各项费用（物质费用+人工费用+投资机会成本+税金）和纯收益（土地总收益-土地总费用）进行分项检查，发现异常数据（采用两倍标准差），并对其进行纠正或剔除，然后对修改后的样点进行统一编号和规范化处理并入库备用按样点的具体位置落实到定级单元图上。经整理后有效样点共11 496个，并运用收益还原法将样点地价修正到农用地基准地价内涵的价格水平，采用年期修正系数、农用地熟化程度、期日修正和区位条件修正系数修正。

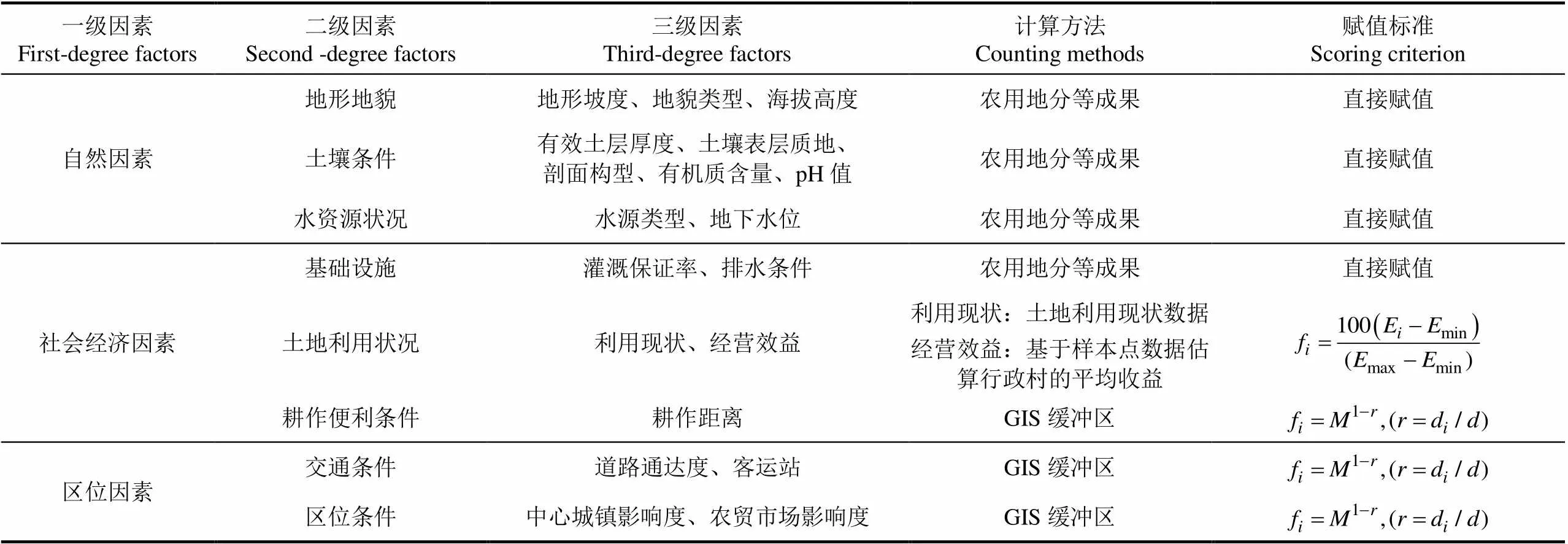
表1 耕地价格评估指标体系

注：式中E为评价单元因子实际值，min为评价单元因子最小值，max为评价单元因子最大值，f是因子的作用分值；=100；为相对距离；d为单元距扩散源的影响半径。

Note: Erepresents the value of factorof assessment unit,minrepresents the minimum value of factorof assessment unit,maxrepresents the maximum value of factorof assessment unit,frepresents the influence grade of factor;=100；denotes the relative distance;ddenotes the influence radius between assessment unit and diffusion source.

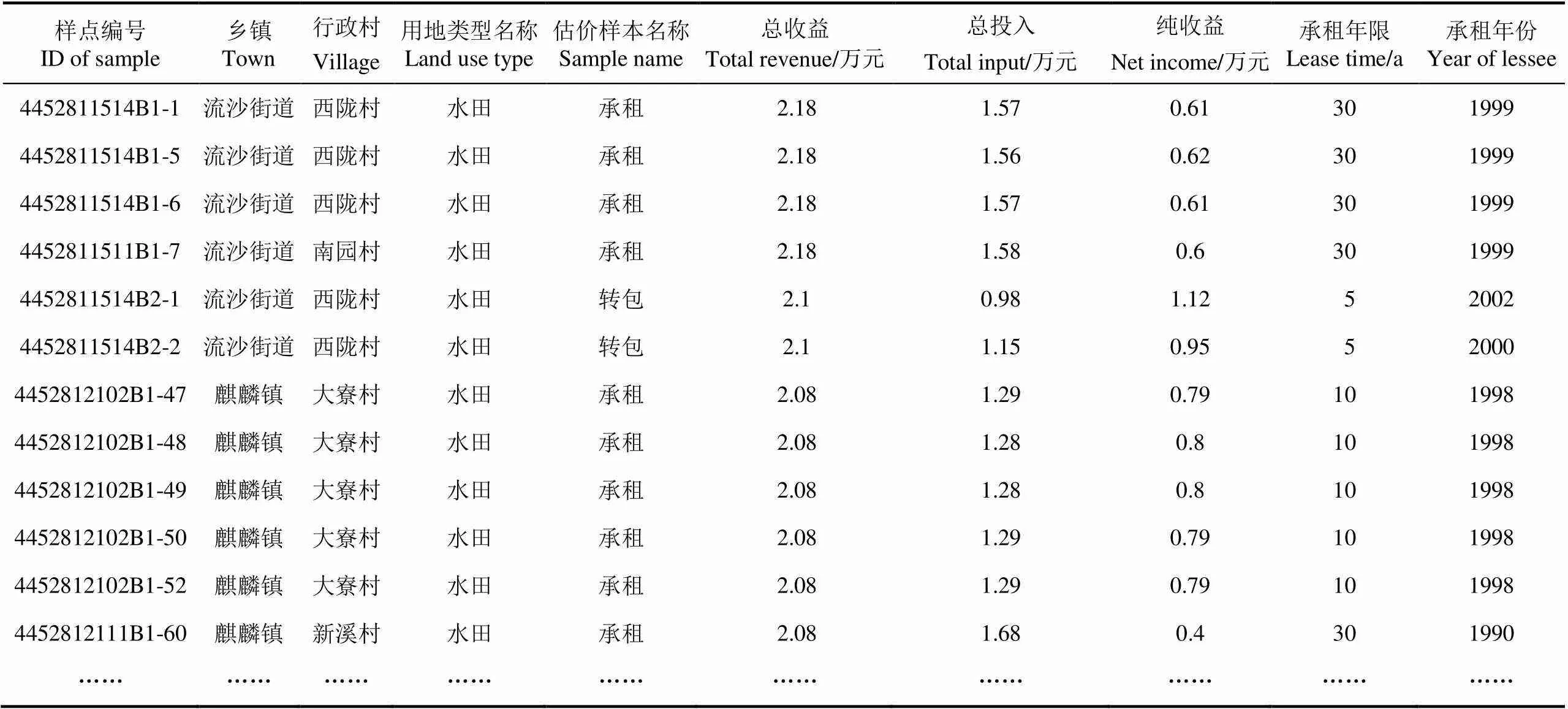
表2 样本点原始资料

3 结果与分析

3.1 试验设置

将样本点集合中的11 496个地价样本点全部进行标注，随机抽取其中10 000个样本作为农用地估价模型的训练样本，剩余的1 496个作为测试样本验证模型性能。BP神经网络模型和SVM模型均为浅层学习结构算法，且已有学者将其应用于基准地价评估研究[14-17]，因此为验证DBN深层网络结构模型的评估性能，本研究实现了两种不同网络结构参数的BP神经网络评估模型作为对比，分别定义为BPANN1和BPANN2，并将SVM模型也设置为对照试验。DBN隐含层数目设置为3，即总层数为5层，每层的神经单元数依次为19-12-6-3-1，先放大特征信号再逐层压缩，最后形成 6 维特征向量进行拟合。DBN模型无监督训练阶段学习率为0.6，迭代次数为200，为动态调整学习率设置初始动量项参数为0.5，中后期调整为0.9。BP神经网络考虑两种情况，BPANN1设置为单隐层结构，隐含层神经单元个数采用遍历法确定，遍历区间为[1,20]，经搜寻，隐层单元设定为10个。BPANN2则采用和DBN一样的网络结构即19-12-6-3-1；DBN 的监督学习阶段和两个 ANN 的训练方式一致，均采用梯度下降算法，学习率设置为0.4，迭代 200 次。SVM取核函数为高斯径向基核，利用6折交叉验证和网格法遍历寻找到最优的惩罚因子C为100，径向基核函数参数为6.4。

试验采用的硬件平台为Intel(R)Core(TM) i7-4600U CPU 4核，主频2.1 GHz，内存16 GB。软件配置为Microsoft Windows 7专业版64 位操作系统，Matlab 2015运行环境。

3.2 评估性能对比

考虑到多层神经网络参数的随机性，将上述3种算法各运行20次，并统计对应的输出误差及相对误差，结果见表3。表中的误差为各次测试的平均值，“输出误差”指根据测试样本的模型地价与实际地价求出的地价中误差（median）、最大误差（max）和最小误差（min），“相对误差”由“输出误差”和“实际地价”计算而得。

表3 不同评估模型的测试结果

由表3的结果可以看出DBN模型的相对误差比BPANN1、BPANN2、SVM 4个模型分别要低3.61%、8.14%、3.12%。相比于BPANN1、SVM模型，DBN的深层架构明显能够更好地挖掘地价样本集的深层特征，其将原始的19维特征抽象成了3维高阶特征进行评估，能够获得比浅层结构更好的拟合精度。此外，DBN与BPANN2模型的网络结构及监督训练阶段的参数设置虽然均保持一致，但两者的拟合精度却相差较多，这是由于DBN模型利用其无监督贪心算法有效的对网络结构参数进行了预训练，显著提高了模型的拟合精度。BPANN2的网络结构参数一般是通过随机化方法来进行初始化，然后通过该网络进行训练，其参数未经过有效优化，所以对样本集合的地价拟合精度较差，DBN与BPANN2的监督训练过程如图5所示。此外，BPANN2的网络结构虽然要复杂于BPANN1，但由于传统训练及反馈系统的误差传播效应导致其复杂参数系统影响整体网络系统的拟合功能，所以其拟合精度反而要比BPANN1低4.53%。SVM的目标函数是一个凸函数，可以保证得到问题的全局最优解，避免了人工神经网络优化频繁陷入局部最优的困扰，所以其拟合精度要比BPANN1略高0.46。

传统的浅层学习方法一般仅依靠监督训练来优化模型参数，当训练样本不足时，模型评估性能不够理想。但本文DBN模型包括RBM无监督训练和BP有监督训练2个训练阶段，理论上来讲可以在样本较少时依然获得较高的拟合精度。本研究通过从样本集合中抽取少量训练样本来测试各个模型在训练样本数量不足时的评估性能。在各模型参数设置同上的情况下，从11 496个标注样本中分别抽取300、600、900、1 200、1 500个样本作为训练样本，剩余的作为测试样本，各模型的测试相对误差如表4所示。

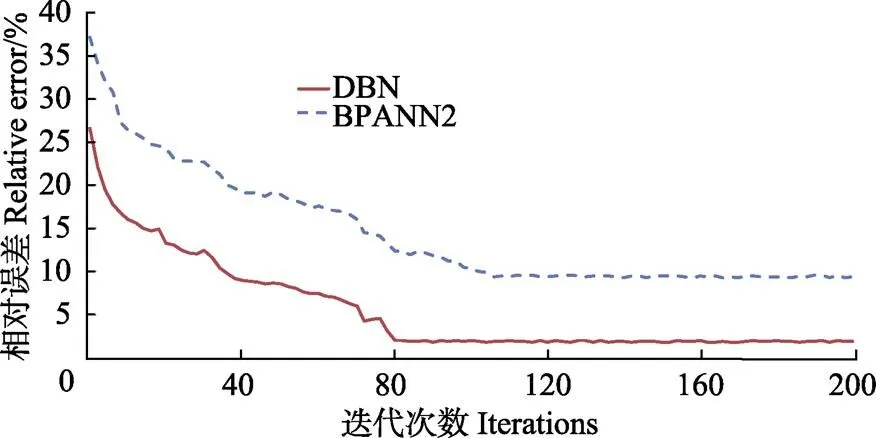
图5 DBN和BPANN2的监督训练过程

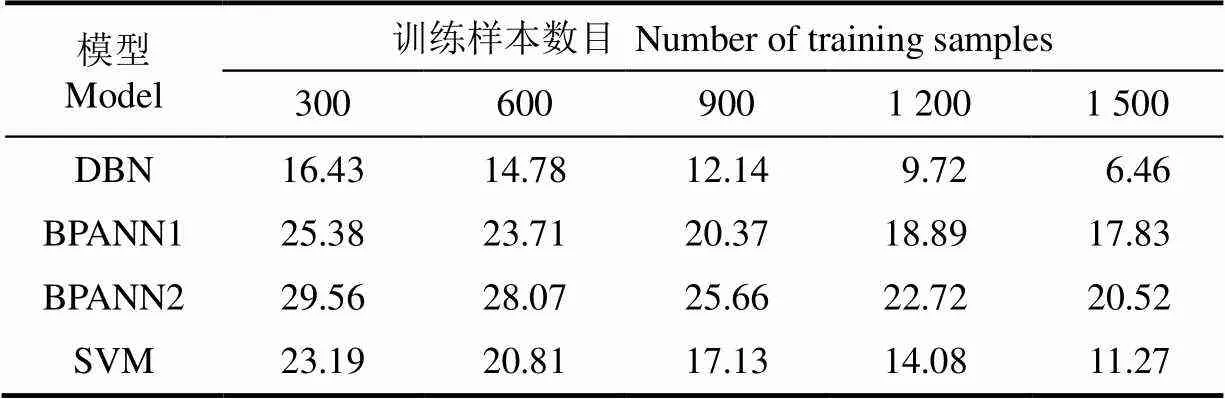
表4 不同训练样本数目的相对误差测试结果

根据表4测试结果可以看出，在训练样本数量较少的情况下，DBN模型显示出了比BPANN1、 BPANN2、SVM模型明显更优越的评估性能。当训练样本数量仅为300时，DBN的相对误差值比上述3个模型低了8.95、13.13和6.76个百分点。随着训练样本数量的递增，各个模型的评估精度都增长明显，DBN模型在训练样本数量为1200时，拟合精度提高到90.28%，而样本数量为1500时，拟合精度已经可以达到93.54%，仍然比其他模型的拟合精度高出4.81～14.06个百分点。SVM模型的评估精度虽然低于DBN但却显著高于BPANN1和BPANN2，这是由于其基于结构风险最小化的训练框架能够在一定程度上客服训练样本不足的问题，但是BP神经网络是基于经验风险最小化的模型，在训练样本数量不足时，网络参数无法得到有效优化，因此其评估精度较低。DBN通过对无标签农用地样本数据的非监督训练来进一步抽象样本集合特征，使得网络结构参数尽量靠近最优区域，因此在有监督训练阶段即使通过少量标注样本的训练也可使模型获得较高的评估精度。综上所述，DBN模型在训练样本数量不足时依然可获得较为理想的评估精度。

上述试验一定程度上说明了DBN的无监督训练过程对于模型评估性能的重要性，本文继续通过改变参与无监督训练的地价样本数量来探讨DBN地价模型评估精度的变化规律。首先固定有监督训练微调阶段的标注样本数量为1 000，然后分别设置RBM无监督训练段的无标签训练样本数量为500、1 000、1 500、…、5 000，每一种参数设置的模型分别运行5次然后求取平均相对误差如图6所示。

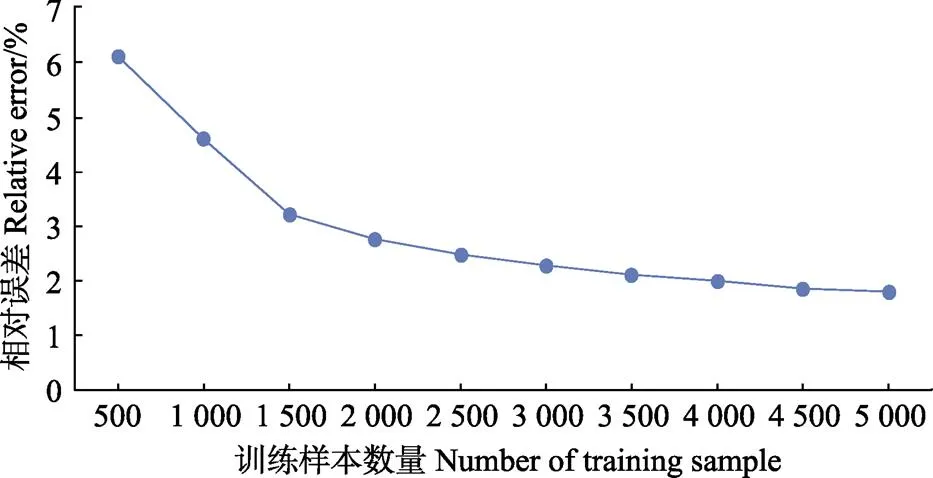
图6 DBN相对误差

由图6可以看出，随着无标签地价样本数量的增加，DBN模型的测试相对误差逐渐降低，即评估精度越来越高，当加入2 000个无标签样本时，评估精度达到了97.23%。从曲线变化趋势来看，在无标签训练样本数从500到2 000的过程中，DBN的评估准确率上升较快，之后的增加趋势较为平缓。总体来看，充分的无监督训练可以有效改善深层网络结构参数，为监督训练微调提供优化后的网络结构，进而提高模型整体的评估精度。

对比4种算法处理10 000个测试数据的运行时间和内存占用率峰值（表5），SVM模型所需时间最短，内存占用率最小，BP神经网络和 DBN 由于隐含层较多，所以运行时间和内存占用率相对较大。尤其是DBN算法的无监督训练及微调训练2个阶段占用计算资源较多，其总体训练时间及内存占用都是最高的。

表5 各类算法运行时间及内存占用率

继续将浅层模型中评估准确率最高的SVM与DBN进行运算效能进行对比。DBN模型依靠1 000个标注样本和1 000个无标注样本可实现95.38%的评估精度（如图6）。而SVM达到95.13%的评估精度需要10 000个标注样本（如表3）。上述两者对应的训练样本所需的计算耗时如表6所示。根据测试结果，达到近似的评估精度，SVM的训练样本仿真耗时为193 s，而DBN耗时187 s，两者耗时基本持平。如果考虑地价评估系统规模扩大时（如增加影响因子或者扩充地价样本库），为达到同等评估精度，SVM会需要更多的标注样本，DBN模型将逐渐体现出更明显的时间优势。

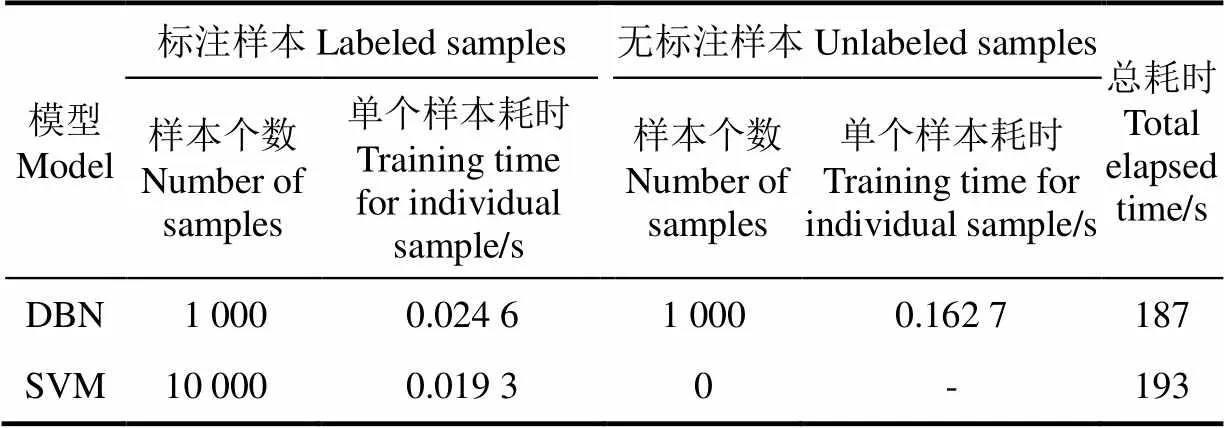
表6 DBN与SVM训练耗时对比

3.3 基准地价评估

在耕地估价特征体系下，根据点、线、面三类因子对评估单元的不同作用方式选择相应的量化方法（可参见农用地定级估价国家规程）计算并构建所有评估单元的特征向量矩阵，并将其输入DBN的深层网络结构，可输出所有评估单元对应的地价，然后利用总分频率法结合当地实际将耕地评估单元划分为5级，然后运用公式（7）可计算得到各级别的基准地价，具体计算结果见表7。

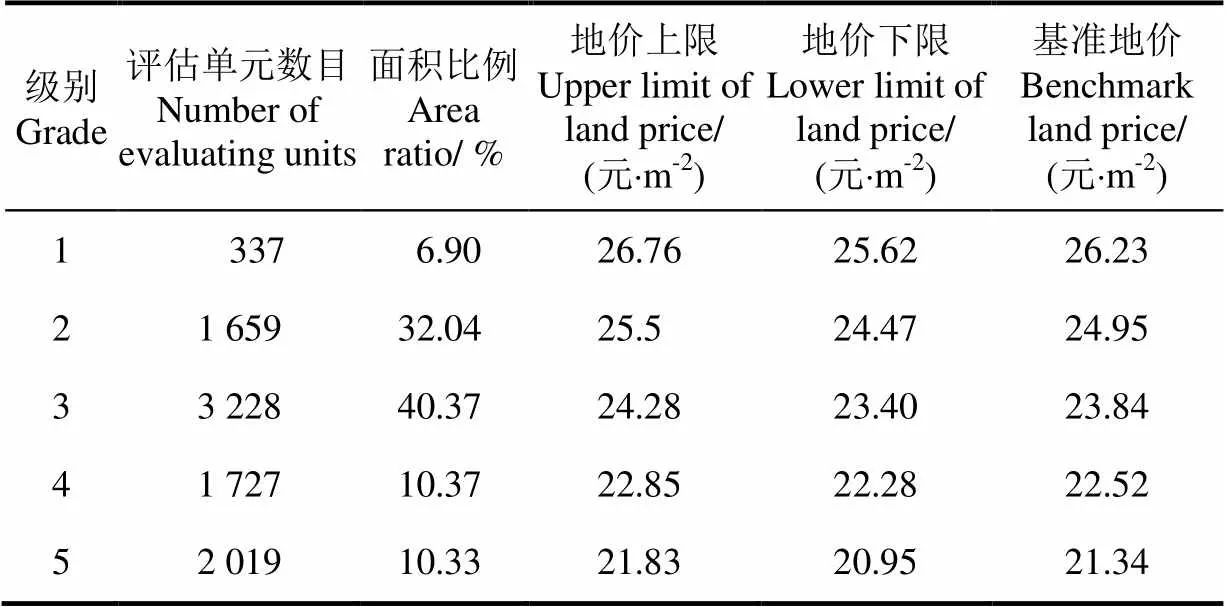
表7 普宁市不同级别耕地基准地价

普宁市农用地基准地价评估DBN模型综合考虑了评价单元的自然条件、社会经济条件和区位条件3方面因素的影响。而耕地质量同样也受3类因素的制约，因此耕地的基准地价成果和分等成果在宏观的空间分布上应该具有较高的一致性。普宁市耕地分等成果（由普宁市国土局提供的农用地分等成果数据）和基于DBN模型的基准地价评估成果的空间分布特征如图7所示：1）从空间位置上看质量最好的耕地分布在普宁中东部和东北部的冲击平原地区，该地区土壤质量较好，自然条件比较优良，是普宁市的粮食主产区，此外该地区也具有较好的区位条件和交通条件，不仅有国道过境，省道和县道相连，而且具有二个1级中心城镇（占陇镇和洪阳镇），7个二级中心城镇（流沙、池尾、下架山、军埠、大坝、麒麟、南溪），4个客运站和5个农贸市场，因此该地区对应的耕地基准地价总体也是最高的，但是该区域也存在耕地质量最优但由于远离主干道路、中心城镇或者客运导致评估单元基准地价级别较低；2）较好的耕地主要分布在东北部丘陵区和中西部丘陵区，该地区土壤耕层较厚，排灌较好，但肥力一般，总体区位和交通条件不十分理想，虽然有省道贯通南北，但是县道较少，中心城镇、农贸市场和客运站数量不多，所以其总体基准地价不高，但也有部分评估单元虽然耕地等别不高，但由于临近国道、省道、中心城镇或者农贸市场，在DBN模型的深层网络映射关系下，最终评估单元也获得了较高的基准地价水平，这也与该区域实际农用地交易情况保持一致；3）最差的耕地主要分布在西南部，此地带土壤耕层浅薄，肥力较差，另外该地区省道较短，主要由县道和农村道路相连，中心城镇、农贸市场和客运站稀少而分散，因此其对应的基准地价也最低。

上述结果表明通过本模型计算所得的普宁市基准地价与耕地质量在空间分布上呈现出较为一致的异质性规律，并且DBN模型在前期训练时能够综合考虑自然质量、交通区位等因素，使得二者的空间分布也存在一定的差异性。

4 结 论

本文针对农用地地价评估问题，提出一种基于深度置信网络的农用地基准地价评估方法。以广东省普宁市农用地基准地价评估为实例，得出以下结论：

1）DBN模型将原始的19维特征抽象成了3维高阶特征进行评估，与BPANN1、SVM这类浅层学习模型相比，其对地价的拟合精度要高出3.61%、3.12%；

2）由于DBN模型借助其无监督贪心算法能够有效对网络结构参数进行预训练，而BPANN2采用随机化方法生成网络参数，因此DBN比具有同样网络结构的BPANN2地价评估精度要高出8.14%；

3）在训练样本只有300时，DBN模型对地价的拟合误差为16.43%，比BPANN1、BPANN2、SVM模型的相对误差分别要低8.95、13.13和6.76个百分点。当样本数量增加至1500时，拟合精度已经可以达到93.54%。此外DBN通过对无标签地价样本数据的非监督训练来进一步抽象样本集合特征，使得网络结构参数能够尽量靠近最优区域，进而提升评估精度；

4）对比10 000个测试样本的训练过程，DBN模型的运算时间高于BPANN1、BPANN2、SVM模型，但内存占用率最少，但在都获取到95%左右的评估精度的情况下，SVM 的训练样本仿真耗时为193 s，而DBN耗时187 s，两者耗时基本持平。

5）在训练完成的DBN网络结构下，求取所有评估单元地价，并采用总分频率法将普宁市耕地评估单元划分为5级，然后利用面积加权法求取对应的级别基准地价范围为21.34～26.23元/m2。通过与普宁市耕地质量等别图对比分析，发现二者之间的空间分布规律具有较高的一致性。

本研究首次将深度学习方法与农用地基准地价评估问题相结合，为地价评估课题的研究提供了新思路。通过对地价样本数据集合的训练仿真结果可以看出DBN模型要比BP神经网络、SVM算法的拟合精度更高，一定程度上可以证明通过DBN求取的基准地价准确度更高，但从现有研究来看现在还缺乏可以直接检验基准地价测算结果精准度的理论与方法，使得本研究的实验效果证明这一部分还不够完善，这也成为下一步研究的重点内容。

[1] 邓南荣，文雅，张金前，等. 农用地估价中土地还原率和社会保障价格的探讨[J]. 农业工程学报，2008，24(增刊1)：164－168. Deng Nanrong, Wen Ya, Zhang Jinqian, et al. Land capitalization rate and social security cost in the evaluation of agricultural land price[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(Suppl.1): 164－168. (in Chinese with English abstract)

[2] 刘跃辰，王秋兵，钱凤魁，等. 灰色模型与回归模型在农用地基准地价评估中的比较分析[J]. 农业工程学报，2010，26(增刊2)：344－348. Liu Yuechen, Wang Qiubing, Qian Fengkui, et al. Comparison and analysis of gray model and regression model in basic prices appraisal of agricultural land [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(Suppl.2): 344－348. (in Chinese with English abstract)

[3] 吴宇哲. 基准地价评估中算术平均方法的应用[J]. 中外房地产导报，2000(9)：52－54.

[4] 张雅杰，唐旭，祝国瑞. 城市基准地价评估回归模型分析与改进[J]. 武汉大学学报(信息科学版)，2004，29(6)： 551－554. Zhang Yajie, Tang Xu, Zhu Guorui. Improvement on evaluation model for base land price[J]. Geomatics and Information Science of Wuhan University, 2004, 29(6): 551－554. (in Chinese with English abstract)

[5] 吴群，温修春，唐焱，等. 模型法在农用地基准地价评估中的应用—以江苏省泰兴市为例[J]. 资源科学，2004，26(5)：68－73. Wu Qun, Wen Xiuchun, Tang Yan, et al. Application of modeling method in datum price appraisal of arable land: a case study of Taixing city in Jiangsu province[J]. Resources Science, 2004, 26(5): 68－73. (in Chinese with English abstract)

[6] 姚慧，郑新奇，江吉星. 基于多元线性回归的宗地地价评估—以东营市为例[J]. 资源开发与市场，2006，22(3)：228－229. Yao Hui, Zheng Xinqi, Jiang Jixing. Study on zone land price estimation based on regressive equation[J]. Resource Development & Market, 2006, 22(3): 228－229. (in Chinese with English abstract)

[7] 王满银，肖瑛，汪应宏，等. 中国基准地价评估近10年研究进展[J]. 华中农业大学学报：社会科学版，2011(6)： 71－75. Wang Manyin, Xiao Ying, Wang Yinghong, et al. Research progress of appraisal of benchmark land price in China in recent ten years[J]. Journal of Huazhong Agricultural University: Social Sciences Edition, 2011(6)：71－75. (in Chinese with English abstract)

[8] 方乃芳. 宗地地价模糊评估的研究[J]. 辽宁工程技术大学学报, 2005, 24(增刊1): 86－88. Fang Naifang. Research on the price of land with blurring valuation method[J]. Journal of Liaoning Technical University, 2005, 24(Suppl.1): 86－88. (in Chinese with English abstract)

[9] Bogataj M, Suban D T, Drobne S. Regression-fuzzy approach to land valuation[J]. Central European Journal of Operations Research, 2011, 19(3): 253－265.

[10] 胡石元，李德仁，刘耀林. 一种新的基于云模型的宗地地价评估方法[J]. 武汉大学学报(信息科学版)，2008，23(9)：983－985. Hu Shiyuan, Li Deren, Liu Yaolin. A new land price evaluation method based on cloud model[J]. Geomatics and Information Science of Wuhan University, 2008, 23(9): 983－985. (in Chinese with English abstract)

[11] 刘耀林，傅佩红. Kriging空间分析法及其在地价评估中的应用[J]. 武汉大学学报(信息科学版)，2004，29(6)：471－474. Liu Yaolin, Fu Peihong. Kriging analysis and its application to urban base land-value evaluation[J]. Geomatics and Information Science of Wuhan University, 2004, 29(6): 471－474. (in Chinese with English abstract)

[12] 聂艳，周勇，曾菊新. 基于Kriging的宜都市农用地基准地价评估研究[J]. 地域研究与开发，2008，27(4)：94－98. Nie Yan, Zhou Yong, Zeng Juxin. Datum land value evaluation of agricultural land of Yidou city based on Kriging spatial analysis[J]. Areal Research and Development, 2008, 27(4): 94－98. (in Chinese with English abstract)

[13] Lewis O M, Ware J A, Jenkins D. A novel neural network technique for the valuation of residential property[J]. Neural Computing & Applications, 1997, 5(4): 224－229.

[14] 刘耀林，焦利民. 人工神经网络的基准地价评估方法研究[J]. 地球信息科学学报，2002，4(4)：1－6. Liu Yaolin, Jiao Limin. Artificial neural network based method for evaluating basic land price[J]. Journal of Geo-Information Science, 2002, 4(4): 1－6. (in Chinese with English abstract)

[15] 吴迪军，刘耀林，黄全义. 城镇基准地价评估的人工神经网络模型研究[J]. 测绘科学技术学报，2007，24(4)：255－258. Wu Dijun, Liu Yaolin, Huang Quanyi. An artificial neural network appraisal model for urban base land price[J]. Journal of Geomatics Science and Technology, 2007, 24(4): 255－258. (in Chinese with English abstract)

[16] Sampathkumar V, Santhi M H, Vanjinathan J. Forecasting the land price using statistical and neural network software[J]. Procedia Computer Science, 2015, 57: 112－121.

[17] 赖红松，吴次芳. 基于GASA优化支持向量机的基准地价测算[J]. 中国土地科学，2008，22(8)：56－61. Lai Hongsong, Wu Cifang. Measurement and calculation on base land price based on GASA-optimized support vector machine[J]. China Land Science, 2008, 22(8): 56－61. (in Chinese with English abstract)

[18] Bengio Y. Learning deep architectures for AI[J]. Foundations and Trends in Machine Learning, 2009, 2(1): 1－127.

[19] Golovko V A. Deep learning: An overview and main paradigms[J]. Optical Memory & Neural Networks, 2017, 26(1): 1－17.

[20] Schmidhuber J. Deep learning in neural networks: an overview[J]. Neural Networks the Official Journal of the International Neural Network Society, 2015, 61: 85－117.

[21] Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504－507.

[22] Hinton G E, Osindero S, The Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527－1554.

[23] Hinton G E. Training products of experts by minimizing contrastive divergence[J]. Neural Computer, 2002, 14(8): 1771–1800.

[24] 刘洁，李宏，高敏华. 农用地定级与基准地价评估研究—以吐鲁番市为例[J]. 中国农业资源与区划，2011，32(2)：6－12. Liu Jie, Li Hong, Gao Minhua. Research on agricultural land classification and datum land price evalution[J]. Chinese Journal of Agricultural Resources and Regional Planning, 2011, 32(2): 6－12. (in Chinese with English abstract)

Establishment of agricultural land appraisal model based on deep belief network

Wang Hua1,2, Luo Ping1, Zhao Zhigang1, Nie Ke1

(1.518034,;2.450002,)

The basic prices of agricultural land appraisal (ALA) has the extremely vital significance on establishing a complete set of agricultural land price system and smoothly carry out land assets, such as reasonable allocation of land consolidation rural land management. Existing models such as artificial neural networks, support vector machines, multivariable regression cannot build the complex function relationship fully between the affecting factors and land prices, and the above-mentioned models with shallow structure have no ability to handle a high-dimensional sample set for land appraisal. So deep learning method was firstly introduced into ALA, and a novel method for ALA based on deep belief networks (DBN) was proposed. A group of 19-dimensional original features reflecting status of land location and quality were employed as inputs, and the land prices were used as outputs of DBN model. The parameters of DBN model were firstly initialized by unsupervised learning method with no-label samples, and then fine-tuned by supervised learning method with labeled samples. The land price of each assessment unit can be calculated by using the well-trained DBN deep neural network with the input of feature vector, and the level of assessment unit can be determined by taking advantage of total value frequency distribution histogram, then the benchmark land price for each level can be calculated via the method of area weighted technique. Take the city of Puning in Guangdong province as a case study, feasibility and validity of the model was validated. The results of the present study indicate that: 1) With respect to the artificial neural networks and support vector machines models, the DBN model get better assessment accuracy with a slight increase of 3.61% and 3.12% because of it is able to take the advantage of feature extraction of deep structure, and can enhance its generation ability by a large amount of no-label land price samples; 2) The simulating error of DBN model for land price appraisal is 16.43% when the number of training samples is only 300, which is less than the artificial neural networks and support vector machines models with a least reduction of 6.76%, DBN model gets high assessment accuracy with a small amount of training samples resorting to its unsupervised learning framework, and the assessment accuracy increases with the number of no-label samples; 3) The running time and memory usage of DBN for single training sample is higher than the artificial neural networks and support vector machines models, and the running time of support vector machines model is 193 and 187 s for DBN model when the assessment accuracy reaches about 95%, both of which are equal because of the DBN model need less training samples than the SVM model; 4) The cultivated land assessment units of Puning city are divided into 5 levels based on the their land price results which are calculated based on the DBN model, and the benchmark land price of Puning city ranges from 21.34 to 26.23 yuan/m2which are calculated based on the area weighted technique. The above experiment results indicate that the assessment accuracy of DBN model is significantly better than the models with shallow structure, and the spatial distribution pattern of benchmark land price and quality level of cultivated land for Puning city are consistent with each other. It is concluded that the method is feasible and effective in measurement and calculation on agricultural base land price.

land use; models; agricultural land appraisal; deep learning; deep belief network; basic land price; Puning

10.11975/j.issn.1002-6819.2018.21.033

F301.2

A

1002-6819(2018)-21-0263-09

2018-01-26

2018-08-10

国家自然科学基金项目资助（41601418）；国土资源部城市土地资源监测与仿真重点实验室开放基金资助课题（KF-2016-02-014）；河南省科技攻关项目资助（172102210539；162102210059）

王 华，博士，讲师，主要从事地理信息系统研究，空间数据挖掘，空间决策支持技术研究。Email：whuwanghua@163.com

王 华，罗 平，赵志刚，聂 可.基于深度置信网络的农用地基准地价评估模型[J]. 农业工程学报，2018，34(21)：263－271. doi：10.11975/j.issn.1002-6819.2018.21.033 http://www.tcsae.org

Wang Hua, Luo Ping, Zhao Zhigang, Nie Ke.Establishment of agricultural land appraisal model based on deep belief network[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(21): 263－271. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.21.033 http://www.tcsae.org