基于神经网络的旋风分离器分离效率研究

胡江玮，陆金桂

(南京工业大学 机械与动力工程学院，江苏 南京 211816)

0 引言

旋风分离器是一种普遍应用于发电、机械、矿山等行业，具有结构简单、分离效率高、性能稳定等优点的设备[1]。

分离效率是旋风分离器的主要工作性能，而旋风分离器的结构尺寸对分离效率有较大的影响。为了设计更高性能的旋风分离器，现阶段人们采用CFD的方式对旋风分离器的结构和性能进行了研究。Khairy等[2]研究了进气口截面宽度对旋风分离器的流场分布和分离性能的影响，孙胜等[3]研究了进气口结构与旋风分离器分离效率之间的规律，多数学者研究了单一结构对旋风分离器分离效率的影响，在多个结构参数变化的复杂情况下，李昌剑等[4]提出了基于响应曲面法的旋风分离器分离效率模型。本文应用计算流体力学Fluent软件对Stairmand HE型高效旋风分离器进行两相流数值模拟，以分离器的多个结构参数为输入，利用BP神经网络非线性拟合强的优点，建立基于神经网络的旋风分离器分离效率模型，旨在预测不同结构参数下的旋风分离器分离效率。

1 仿真计算

1.1 计算模型

旋风分离器的结构看似简单，但内部却存在复杂的三维湍流运动，需要对模型进行一定的简化。进行数值模拟计算时先把空气当做是连续相，颗粒视为离散相，计算的步骤是先对连续相的流场进行求解，接着再添加离散相，依据离散相颗粒受力方程获得颗粒的运动轨迹。

连续相采用RNG模型计算。其湍动能和耗散率方程[5]为：

(1)

(2)

其中：

μeff=μ+μt

(3)

(4)

式中：Gk为由平均速度梯度引起的湍动能；Gb为由浮力影响引起的湍动能；YM为可压缩湍流脉动膨胀对总耗散率的影响，αε、αk分别为湍动能和耗散率的有效普朗特数的倒数。

在Fluent中，针对颗粒体积分数<10%的气-固两相流的模拟通常使用离散相模型(DPM)进行计算，用随机轨道模型对颗粒运动进行追踪，在拉格朗日坐标系下，颗粒轨迹求解微分方程为：

(5)

其中：

(6)

(7)

(8)

式中：u为流体相速度，m/s；μp为颗粒速度，m/s；μ为流体动力黏度，Pa·s ；ρ为流体密度，kg/m3；ρp为颗粒密度，kg/m3；dp为颗粒直径，mm；Re为相对雷诺数；CD为曳力系数；gx为X方向重力加速度，m/s2；Fx为X方向的其他作用力，N。

1.2 旋风分离器模型

本文以Stairmand HE型高效旋风分离器为对象，建立三维实体模型，进行数值模拟计算。旋风分离器的结构模型如图1 所示，表1为旋风分离器初始结构参数。

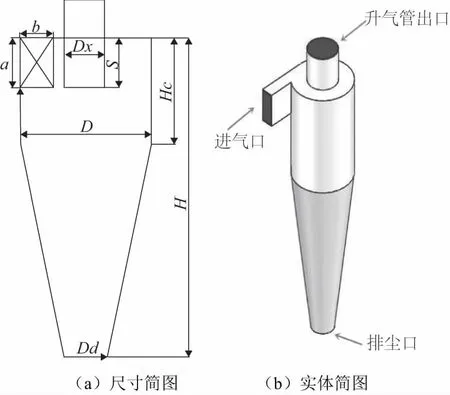
图1 旋风分离器结构模型

表1 旋风分离器的几何尺寸 mm

1.3 边界设定

旋风分离器模型入口速度设置为16 m/s；升气管出口设置为自由流出(outflow)，流量为1；排尘口设置为自由流出(outflow)，流量为0；湍流强度设置为10%；流体介质设置为空气，密度为1.094 kg/m3，黏度为1.789×10-5Pa·s；固体颗粒密度为2 100 kg/m3，质量流量为0.001 kg/m3；选择PRESTO法对压力梯度进行处理，采用二阶精度QUICK差分格式，压力耦合选择SIMPLE算法处理[6]。

1.4 分离效率

对于分离效率的计算采用颗粒跟踪法。当颗粒射入分离器时便开始跟踪，经过分析粒子在分离器内的运动情况，将碰到排尘口的颗粒看作是被捕集、除掉的颗粒；碰到升气管上端面的颗粒被认为是逃逸的颗粒。这样总分离效率由式(9)所得：

(9)

2 数值仿真计算结果

通过数值模拟得到了流场和粒子轨迹的计算结果。Y=0剖面上的切向速度云图如图2 所示。切向速度在轴心处接近于0。Z=791截面上的速度矢量图如图3 所示。从图3中可以看出，在旋风分离器内部气流大致可分为2 个区域，即外旋转气流和内旋转气流。

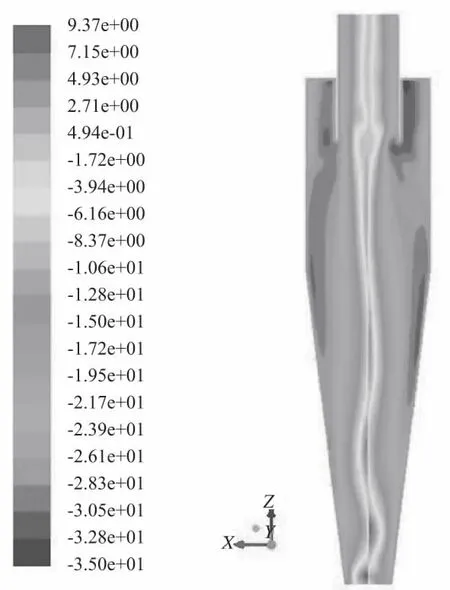
图2 Y=0剖面上的切向速度分布

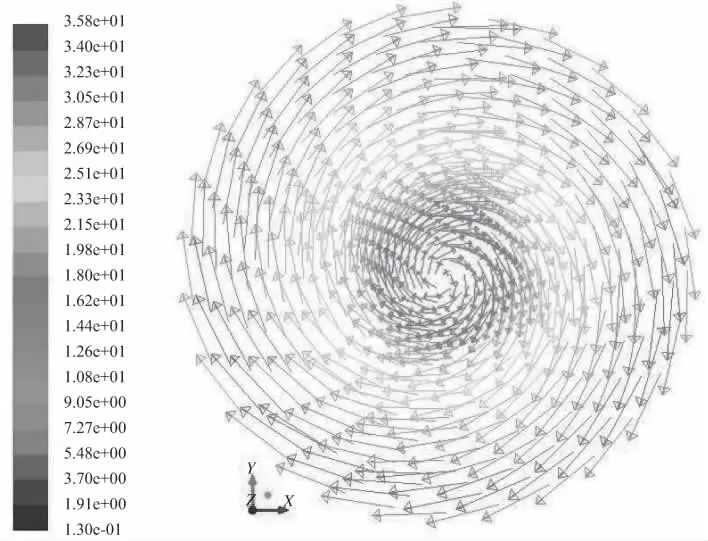
图3 Z=791圆柱和圆锥交界面上的速度矢量

旋风分离器内1～100μm粒子的运动轨迹图如图4 所示。颗粒在旋风分离器中的运动状况非常复杂，且带有很大的随机性，其运动轨迹随着颗粒粒径的不同而有较大变化。

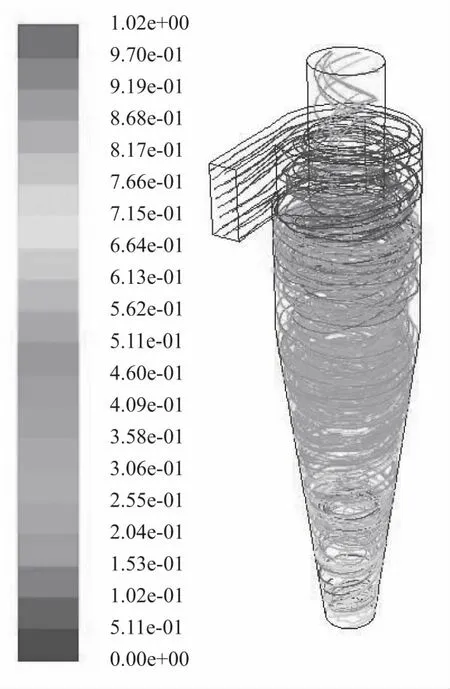
图4 粒子运动轨迹

Y=0剖面上压力分布云图如图5所示。从图中可以看出，剖面上压力由轴心向壁面方向不断增大，存在明显的径向梯度，这是由旋流中离心力造成的。

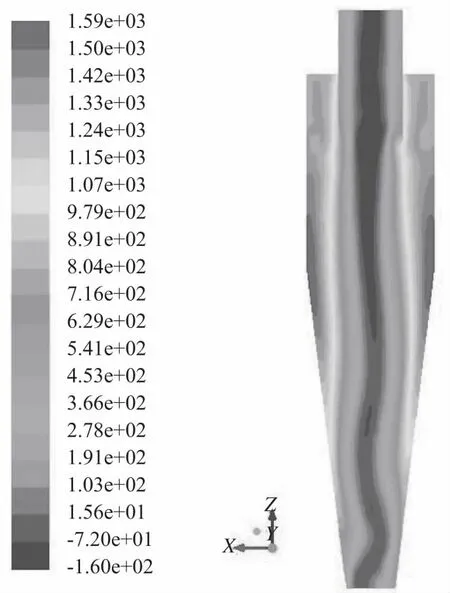
图5 Y=0剖面上压力分布

3 分离效率的神经网络预测

BP神经网络是一种包括输入层、隐含层及输出层的三层神经网络。网络上下层之间实现权连接，而每层节点之间没有连接，输入参数正向传播，误差逆向传播。BP神经网络是一个具有高度非线性的信息处理系统，能对旋风分离器的结构参数和分离效率之间的非线性关系进行学习。通过学习样本输入和输出值，设计网络的隐含层与每层的结点，并设定学习速率和允许误差，然后进行训练[7]。BP神经网络的容错能力能容纳计算分离效率过程中的不确定因素，并对结构参数和分离效率之间的非线性关系建模，其泛化能力能够预测旋风分离器在其他参数水平下的分离性能。

3.1 旋风分离器设计参数的选取

为了建立神经网络分离效率模型，参考一定的文献，选取了对旋风分离器分离效率影响较大的3个结构：排尘口直径Dd、直筒段高度Hc、升气管直径Dx，把与分离器筒体截面直径D的比值即Dx/D、Dd/D、Hc/D作为神经网络输入层[8]。表2为3个结构参数的取值范围。

表2 主要设计参数的取值范围

把设计参数的最小值、中间值、最大值定为三水平，建立以Dx/D、Dd/D、Hc/D为输入，以分离效率Z为因变量的17个实验样本组，其中前12组为BP神经网络模型学习训练组, 后5组为模型验证组对建立的神经网络模型进行验证。表3列出了1-12组的样本参数。

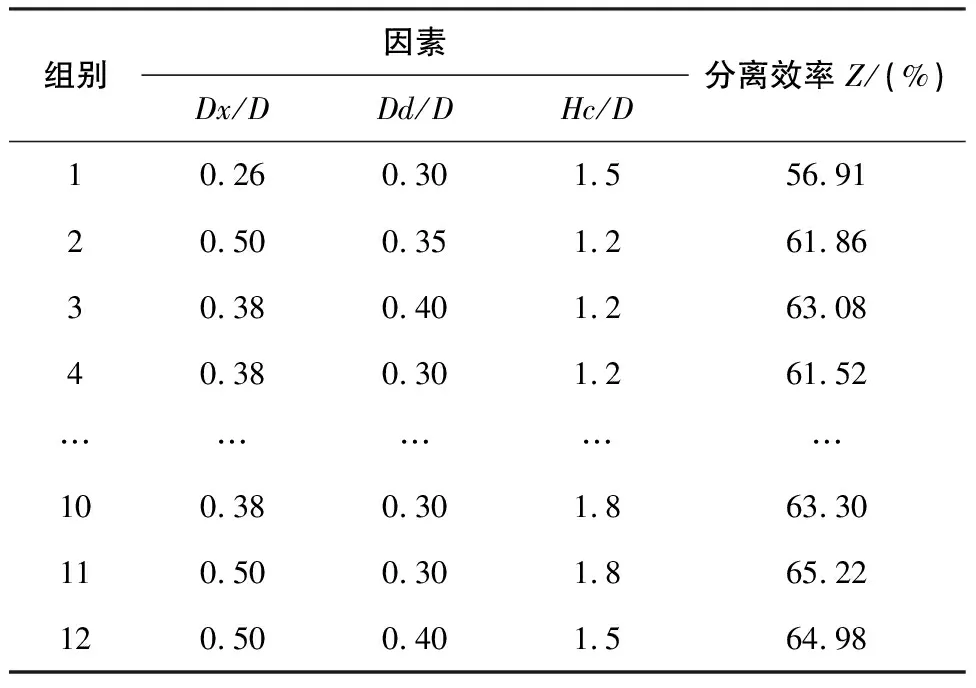
表3 神经网络模型学习训练样本

3.2 BP神经网络参数设定

神经网络的隐含层节点数在神经网络中有着重要的地位，节点的数目影响着神经网络的学习和训练精度，节点数目太少会使神经网络的容错能力变差，而节点数太多会延长网络的学习时间从而会导致误差变多。本文隐含层节点数目计算方法：

N=2n+1

(10)

式中，N为隐含层节点个数，n为输入层节点个数。因为本文的输入层的因素个数为3，所以隐含层节点个数经计算定为7。同时学习速率也会对神经网络产生重要的影响，学习率太小，神经网络能够收敛，但是速度太慢耗费时间；而学习率太大，学习速度就会变得很快，有可能导致振荡或发散。此处设置学习率为0.1。神经网络的误差设置根据训练和研究的问题所决定，此处设置误差率为0.001。

3.3 建立神经网络模型

确定BP神经网络的结构，学习速率等设置参数，样本数据进行归一化处理后，对样本进行学习训练，得到训练好的神经网络模型。

3.4 预测结果分析与比较

使用训练完成的神经网络来对后5组数据完成分离效率预测，预测值见表4。进行分析后，得到BP神经网络预测的相对误差均<5%, 结果表明，BP神经网络在预测旋风分离器分离效率还是相当可靠的。

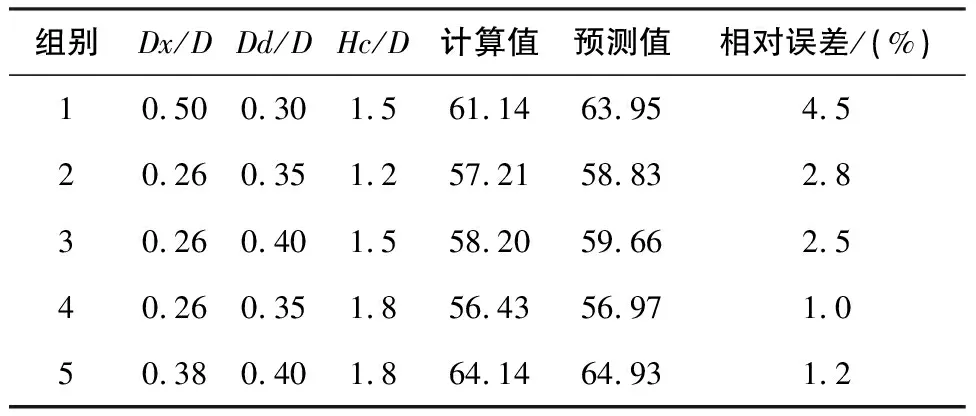
表4 模型预测结果与实验值比较

4 结语

1) 通过FLUENT对旋风分离器进行两相流数值模拟，建立基于神经网络的旋风分离器分离效率模型。用5组数据验证神经网络分离效率模型，预测误差<5%，模型的预测值与模拟结果吻合较好，表明建立的神经网络模型是可行的，为旋风分离器的分离性能计算提供了新方法。

2) BP神经网络模型具有结构简单，预测精度高的优点，可以快速地预测旋风分离器的分离效率，为旋风分离器的性能优化设计提供了参考依据。