围壳形状对潜艇流致噪声的影响计算

王开春, 马洪林, 赵 凡, 官 睿

(中国空气动力研究与发展中心 空气动力学国家重点实验室, 四川 绵阳 621000)

0 引 言

潜艇在航行中存在各种噪声，如：流动噪声、螺旋桨推进器噪声、发动机噪声等。随着噪声探测技术的飞速发展，在未来的海战中潜艇隐身性能是决定战争胜负的关键因素，有效降低潜艇的噪声已经成为潜艇研究主要课题。近年来，随着计算机技术和CFD技术的发展，采用数值方法开展气动声学研究其成熟度不断提高，同时把气动声学的研究成果应用于潜艇流致噪声研究也成为可能。研制相应的计算分析软件，对于静音潜艇的选型设计具有重要的工程价值。

采用CFD方法进行噪声计算的主要有：计算气动声学(CAA)[1-2]、声比拟方法等。CAA方法就是直接从CFD结果中提取所有的声音信息；通过声观测点的位置来监控直接获得声压的波动，并捕捉声的反射、散射等声学现象，需要无反射的边界条件[3]。CAA要求保持足够的时间与空间精度，计算网格规模大、时间步长小、计算耗时长；通常采用空间4阶以上的高精度计算格式[4]，稳定性差，容易发散。声比拟是另一类噪声计算方法，声学比拟理论[5]由Lighthill 1952年提出，用于处理喷流噪声问题。Curle[6]、Ffowcs Williams与Hawkings[7]等进行了推广，相继加入静止固体边界和运动边界的影响。声比拟的实质就是使用CFD精确模拟声源附近的瞬态流场，从瞬态(LES、DES、URANS) CFD 计算中提取源信息[8]，通过分析求解波动方程来模拟噪声从声源到接收者的传播过程。相比于CAA，声比拟耗时较少，计算格式精度不必象CAA那样高，适应复杂外形的计算。声比拟理论将流场与声场分开处理，无法考虑流场与声场之间的相互作用。

国内在潜艇流致噪声数值计算研究方面起步较晚，直到20世纪90年代，潜艇流致噪声的数值计算研究才开始逐步发展起来。早期的研究也多是涉及到计算方法等探索性工作，后来较多见的是利用商用软件采用声比拟方法开展一些具有工程意义上的计算研究[9]。但在大尺度、复杂外形、超大规模网格的计算方面文献不多见。

针对潜艇流致噪声数值计算问题，本文基于迭代时间推进方法、DES模拟湍流方法、超大网格规模并行计算技术等，建立了高精度脉动压力与噪声计算方法与程序。应用该程序对潜艇SUBOFF[10]放大模型的四种不同围壳后缘形状，开展了流致噪声影响计算，并依据梯形布局设计的降噪思想，提出了一种具有较好降噪效果的围壳后缘形状。

1 数值计算方法简介

潜艇流致噪声的计算思路：先开展稳态流场计算；在此基础上开展非定常流场求解，获得脉动压力等瞬态流场结果；最后采用声比拟方法获得声观测点随时间变化的声压。

稳态流场计算采用本课题组自主研制的低速流动计算软件WS3D[11-13]。该软件采用多块技术与SIMPLE算法求解不可压N-S方程，处理复杂外形与复杂流动能力强，计算精度和效率高。因此该软件在大型军用、民用运输机的低速气动特性、舰尾流与飞机着舰、汽车、磁浮列车、高铁与城际列车等空气介质的计算中得到应用，并取得较好结果。同时，软件在水动特性的计算中也获得应用，曾开展了三峡坝区非定常摆流计算、潜艇的阻力计算以及非定常脉动压力与噪声计算。

1.1 流场计算方法

低速流动的控制方程为不可压N-S方程，其通用形式为：

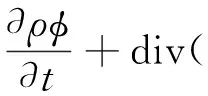
其中，φ为输运变量，ρ为流体密度，V为流体速度，Γφ为扩散系数，qφ为源项，φ、Γφ和qφ取不同值，可代表空气的连续性方程、动量方程和其他标量(如温度、湍动能等)的输运方程。

数值计算方法：采用有限体积法，离散后方程组求解采用SIP强隐式算法；不可压的计算方法采用SIMPLE系列算法; 采用结构网格的多块对接技术与多窗口技术处理复杂外形和边界；湍流计算采用两方程的k-ε模型，近壁区采用低Re数修正与壁面函数相结合的方法处理。方程中各项的物理意义、具体表达式以及数值方法可参见文献[11,14,17-18]。

脉动压力的精确计算是潜艇流致噪声的关键，在技术上难度很大，对高质量的网格生成、计算方法的精度、湍流模型等方面提出了很高的要求。为此本文在计算软件WS3D中采取了如下措施：1) 采用三阶迎风格式处理对流项，中心差分格式处理扩散项和源项，以提高计算精度；2) 非定场计算中采用迭代时间推进法[15]，该方法属于非定场求解中PISO类算法，即在每个物理时间步内添加了多次迭代，适用于非定场流动问题的求解；3) 超大网格规模(高达亿量级)的并行技术，并行计算中采用贪婪算法实现负载平衡与划分，采用并行的SIP算法实现流场求解，提高计算效率；4) 湍流计算采用DES模型，由于URANS求解获得的脉动量的信息比较有限，而DES模拟在获得固体表面的脉动压力具有一定的优势。在低雷诺数k-ε模型中[16]，其湍动能方程为：

将方程(2)的中的消失项ρε改为：

ρε=ρk3/2/lDES(3)

其中lDES为RANS和LES长度尺度中的较小值，其表达式为：

lDES=min(lke,lLES)(4)

lke=k3/2/ε(5)

lLES=CDESΔmax(6)

Δmax为单元网格边长(Δx、Δy、Δz)的最大值。在具体计算中，为了达到DES模拟的延迟的效果，先用RANS方法算出稳态流场，非定常计算中再采用DES模型。

1.2 声场计算方法

本文潜艇流致噪声的模拟方法为声比拟方法。其最通用的声学积分公式FW-H方程为：

p′(x,t)=p(x,t)-p0

其中，p′(x,t)为观测点的声压，右端第一项为空间流体脉动项(即四极子源)，右端第二项为固体表面脉动项(即二极子源)，右端第三项运动壁面所产生的单极子源，单极子属于短距项。x为声观测点，y为声源位置,li为固体表面单位外法向量，a0为介质声速，当水介质时取声速为1500 m/s。R为声源到声观测点之间的距离，表达式为R=|x-y|。Tij为Lighthill应力张量，表达式为：

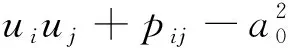
在低马赫数流动，固体表面的偶极子声源处于主导地位，四极子源是很小的量，在计算中没有考虑四极子源。本文计算中FW-H积分面选取的是整个潜艇表面。

2 不同围壳形状流噪声计算

2.1 计算软件验证

为了验证流场软件，开展SUBOFF潜艇模型阻力验证计算，该潜艇模型是美国国防高级研究计划署资助的SUBOFF计划所用模型[10]，它包括主艇体、指挥台围壳，对称翼型十字型尾翼。表1提供了本软件计算阻力结果与试验比较，两者吻合较好。

为了验证噪声计算软件，开展了汽车后视镜模型[8]验证计算，图1提供了本软件汽车后视镜表面脉动压力分布云图，图2提供了本软件计算的典型声测点声压级频谱图。本软件计算的典型声测点最大声压级为81.7 dB，试验值为79 dB，结果表明：本软件计算的最大声压级的误差在3 dB左右。

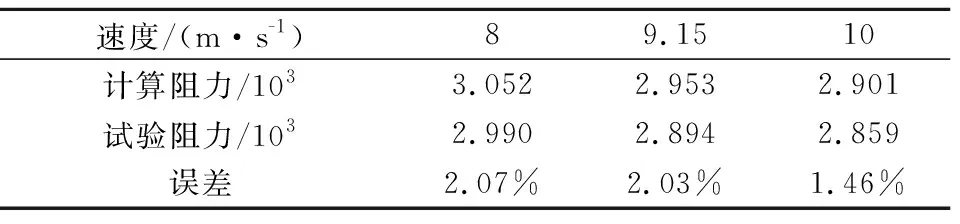
表1 潜艇SUBOFF模型阻力计算与试验比较Table 1 Comparison of drag for SUBOFF model

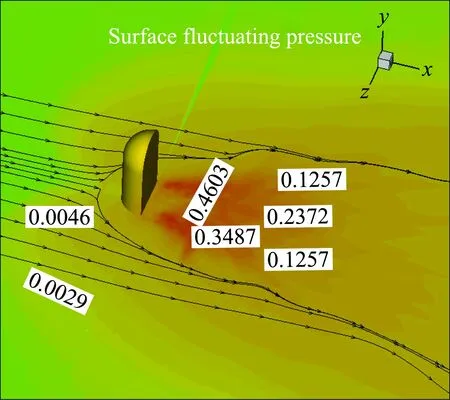
图1 汽车后视镜表面脉动压力云图Fig.1 Contours of surface fluctuating pressure

图2 汽车后视镜典型观测点声压级频谱Fig.2 Frequency spectra at typical observation point

2.2 计算外形及网格

美、俄等国在其先进潜艇的围壳设计上都有采用梯形布局的型号，为了研究这种围壳梯形布局的降噪机理与效果，基于本文所开发的潜艇流致噪声计算程序，在潜艇SUBOFF放大模型的基础上，开展了四种指挥台围壳后缘形状的声场计算研究。

考虑到声学存在尺度效应，本文计算中把SUBOFF潜艇模型放大到通常潜艇的尺寸，放大比例为10.6952∶1，此时计算的艇长98.5985 m，最大直径11.496 m。放大后的原型为“jb”，其围壳的根弦长度8.2723 m。

改型主要是把围壳由矩形变为梯形，在围壳的根弦长度与后缘处进行修改，围壳的顶部弦长和高度保持不变。三种改进型分别为：jb-m1、jb-m2、jb-m3。根弦长度分别为：10.1997 m、11.5668 m、12.5668 m。如图3，坐标原点取为艇体头部中心，坐标轴：x轴为艇身方向，y轴为艇身高度方向垂直向上，z轴为水平尾翼翼展方向按右手系确定。计算采用多块对接网格，网格规模为1.02亿，图4显示了计算的四种围壳外形及其典型围壳的表面网格。

图3 计算外形及坐标方向Fig.3 Submarine configuration and frame

图4 四种围壳外形与jb-m2表面网格Fig.4 Four fairwaters shapes and surface grid of jb-m2 model

2.3 流致噪声计算结果分析

对四种不同围壳外形开展了流致噪声计算，它们的计算条件相同。即：潜艇航行速度7.2 m/s，迎角与侧滑角均为0°。图5给出了声压观测点位置示意图，声压观测点共有2个系列，其中1系列观测点在水平方向上距艇中心线10 m，间隔4 m，共26点；2系列观测点在距艇头部53 m处的横截面的圆周上，圆的半径10 m，角度间隔10°，共36点。

图5 声观测点Fig.5 Acoustic observation points

把固体表面脉动压力的时均均方根值[8]按照声压级计算方法处理，可获得脉动压力声压级。表面脉动压力声压级可直观显示声源在固体表面的分布。图6给出了潜艇jb、jb-m2两个模型表面脉动压力声压级分布云图，计算可见：1) jb模型艇身表面的脉动压力级比jb-m2模型在相同位置的表面高出2 dB左右；2) 围壳表面及其附近的艇身表面区域出现较高的表面脉动压力声压级，说明围壳是重要的声源区；3) 潜艇尾部的局部区域因流动分离也出现了较高的表面声压级。

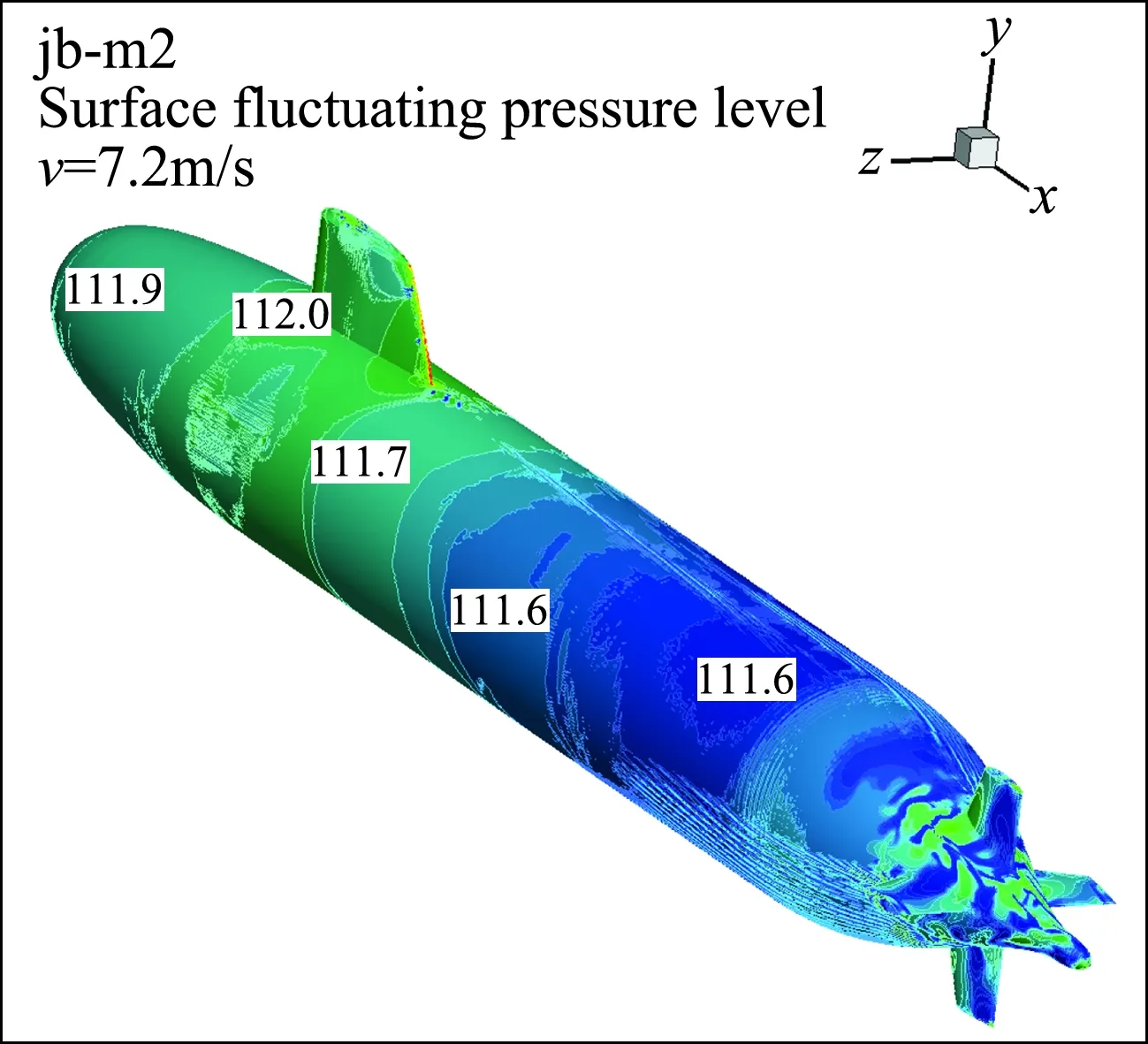
图6 潜艇jb与jb-m2模型表面脉动压力声压级云图Fig.6 Contours of fluctuating pressure level on surface of jb and jb-m2 models

图7给出了首尾视角下潜艇jb与jb-m2模型绕围壳流动的空间流线与压力云图。计算可见：1) 在jb模型中水流绕过围壳后，没有直接到达潜艇后部的垂直尾翼上，而是产生了一定的偏流，说明该模型的围壳尾流产生非对称流动；2) 在jb-m2模型中，围壳顶部和根部的尾流均能够到达潜艇后部的垂直尾翼上，偏流现象得到了明显改善。

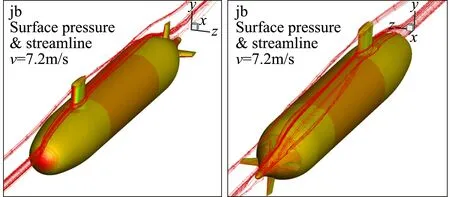
正是围壳尾流的左右摆动，引起围壳与艇体周围流场的较大变化，并使围壳与整个艇体表面产生了较大的脉动压力。本文通过改变围壳后缘形状，采用梯形布局来抑制围壳后尾流的摆流，从而降低整个艇体表面脉动压力与噪声源强度，达到降噪目的。

图8给出了潜艇四种围壳外形在观察点1系列中的总声压级比较。由此可见：1) 三种改进的围壳外形在总声压上均有不同程度下降，其中降噪效果较好的是jb-m2模型，与原模型相比总声压下降在7 dB左右，jb-m3模型总声压下降在5 dB左右，jb-m1模型总声压级下降在3.6 dB左右；2) 观察点1系列中声测点7～18(距潜艇头部24～68 m)范围总声压级较高。

图9给出了四种围壳外形观测点1系列中典型测点声压级随频率的变化比较，其中jb模型的最大声压级为108.4 dB，jb-m1模型最大声压级为107.8 dB，jb-m2模型最大声压级为103.0 dB，jb-m3模型最大声压级105.8 dB。由此可见：jb-m2模型最大声压级比原模型降噪5.4 dB，降噪效果在三个模型中最佳。其次是jb-m3模型，降噪2.6 dB。

图8 四种围壳外形观察点1系列处总声压级比较 Fig.8 Comparison of total sound pressure level among four fairwater shapes at observation point series 1

图9 四种围壳外形测点1系列处典型声压级频谱图比较Fig.9 Comparison of frequency spectra among four fairwater shapes at observation point series 1

图10给出了潜艇四种围壳外形在观察点2系列处的总声压级比较，其中jb模型的总声压级最大， jb-m2模型降噪效果较好，与原模型相比总声压下降在7 dB左右，jb-m3模型总声压级下降在5 dB左右。jb-m1模型总声压级下降在3.3 dB左右。

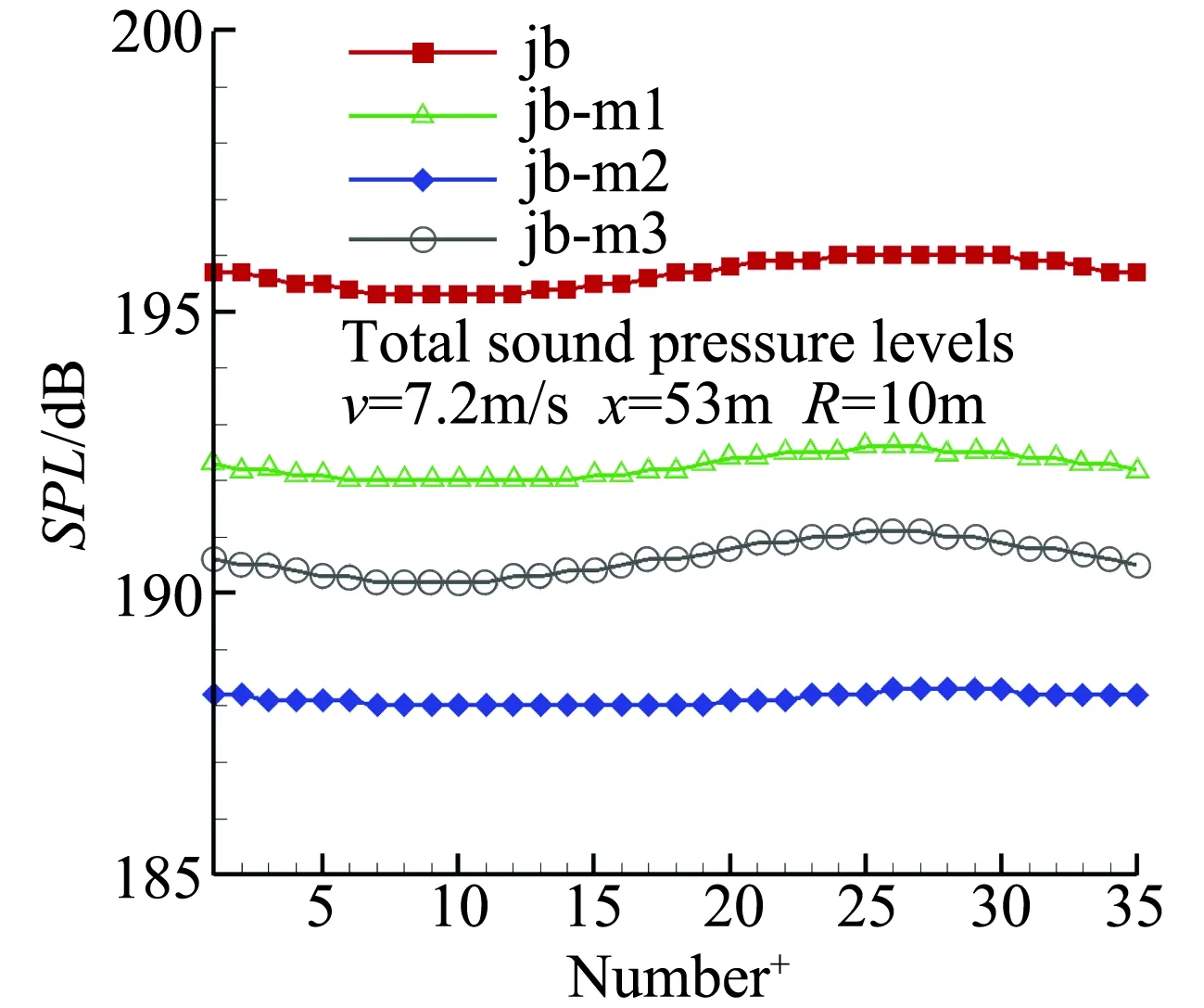
图10 四种围壳外形观察点2系列处总声压级比较 Fig.10 Comparison of total sound pressure level among four fairwater shapes at observation point series 2

图11给出了四种围壳外形观测点2系列中典型测点声压级随频率的变化比较，其中jb模型的最大声压级为108.2 dB，jb-m1模型最大声压级为107.4 dB，jb-m2模型最大声压级为102.6 dB，jb-m3模型最大声压级105.6 dB。jb-m2模型最大声压级比原模型降噪5.6 dB左右。

图11 四种围壳外形测点2系列处典型声压级频谱图比较Fig.11 Comparison of frequency spectra among four fairwater shapes at observation point series 2

3 结 论

本文建立了适用于潜艇流致噪声计算的方法和计算程序，对四种不同围壳后缘形状的潜艇模型进行了流致噪声计算，得到如下结论：

1) 本文所提出的流致噪声计算程序在潜艇阻力计算上有较高精度，在噪声计算上最大声压级误差约为3 dB，可满足工程应用中噪声选型的需要；

2) 潜艇围壳后缘形状从矩形变为梯形，能有效降低潜艇流致噪声。围壳的三种改型中，最大的降噪效果可达5 dB左右；

3) 通过分析潜艇表面脉动压力声压级分布、空间流线、声测点处总声压级等计算结果，初步揭示了梯形围壳降噪机理，即梯形布局的围壳可抑制其尾流的摆动，达到降低潜艇表面脉动压力与声源强度效果，为静音潜艇的设计提供了一种思路。