人工快速土壤渗滤系统滤池高度计算模型的构建
姚雪倩,李云祯,曾拯康,许文来
(1.四川省地质工程勘察院,四川 成都 610031;2.四川省环境保护科学研究院,四川 成都 610041;3.成都理工大学环境与土木工程学院, 四川 成都 610059)
1 引沿
人工快速渗滤系统的滤池高度关系着污染物的降解能力,所以滤池过低,污染物浓度降解难以达标;滤池过高,建造成本会大大增加,而人工快速渗滤系统的滤床高度需要根据一些具体的处理目标和要求以及填料情况进行选择判断,目前却大多数用经验来判断大致的滤池高度。Hydrus可以较为准确的模拟污染物的运移,并科学的计算出人工快速渗滤系统的最适高度[1]。
2 材料和方法
2.1 实验室模型构建
计算机数值模拟方法研究污染物长期运移机理,并分析影响因素理论上是科学可行的。但在实际情况下,土壤结构具有明显的不确定性,而所建立的模型都是确定性模型,其研究结果与实际情况有较大偏差,因此无法准确真实的反应出实际情况下的准确参数。所以,在运用计算机数值模拟方法研究污染物长期运移机理时应添加一组真实的实验进行模拟、校正。
由于各种条件的限制,无法使用真实的人工快速渗滤系统进行实验,只有将人工快速渗滤系统等比例缩小,采用模拟沙柱的形式进行实验。
所使用的模拟沙柱填料应尽量模仿实际人工快速渗滤系统中自然条件下的填料。模拟沙柱上应有较多的,均匀排布的排水孔[2],以便取得不同高度的出水进行测量。进水时应保证连续,均匀,保证污水流经尽量多的填料。
本实验所采用的模拟沙柱为150 cm高,半径为6 cm的塑化玻璃柱。内部填充物为模拟自然条件下的中砂,填充物填充了105 cm的高度。沙柱每隔5 cm存在一个取水口,用于取出不同高度的出水,见图1。
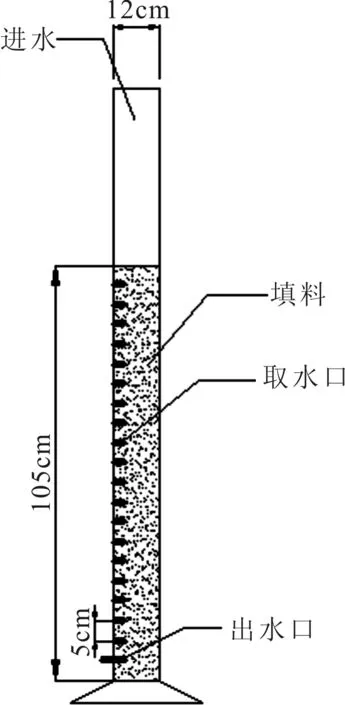
图1 实验装置示意
2.2 沙柱数据测量
本实验所采用的模拟沙柱为150 cm高,半径为6 cm的塑化玻璃柱。内部填充物为模拟自然条件下的中砂,填充物填充了105 cm的高度。
取出部分填充物,放入坩埚中,称量。放入马弗炉550度烘干2 h,取出称重。根据前后重量差,计算出残余含水率θr。
取出全部填充物,称量出质量。堵住出水口,向模拟沙柱中通入水至水刚好淹没填料且液面不再下降,记录用水体积,算出用水质量[3],计算出饱和含水率θs,孔隙度n。
向沙柱中连续进水,直到出水量均匀,稳定后,测量相关数据,计算出柱内填充物的渗透系数。
填充物的渗透系数计算过程如下:
V=Q单/A
(1)
式(1)中,V为单位时间的流速;Q单为单位时间的流量;A为过水断面面积。
I= (H1-H2)/L
(2)
式(2)中,I为水力梯度;H1-H2为水头高度;L为水位高度。
K=V/I
(3)
通过对沙柱的测量,计算,再将(1)、(2)的结果带入(3)中,Q单=260 mL/s,V=0.05 cm/s,L=85 cm,H1-H2=81 cm得出:K=0.053 cm/s。
2.3 Hydrus软件所需CRI系统参数
Hydrus-1D水流模块中的SoilCatalog项目包含12种典型土壤材料,如沙子,淤泥和粘土,以及与土壤湿度特性曲线有关的参数[4]。该软件还提供了预测土壤中的土壤和沙子的神经网络算法[5]。根据实际参数,模拟沙柱水分特征曲线参数如表1所示。

表1 土壤水分特征曲线参数值
3 结果与讨论
通过实验室测试的方法得出不同浓度进水COD对应的CRI滤池最适高度见表2Y轴,运用Hydrus软件模拟的不同浓度进水COD对应的CRI滤池最适高度见表2Z轴,进水浓度见表2X轴。
将表2中的数据输入Origin中,采用曲面拟合,得到已知进水COD浓度,可对应出实际最适滤床深度与理论滤床最适深度的曲面数学模型(图2)。
4 结论
本研究建了这个模型,可以在上面找到任何一个点,所对应的一个进水COD浓度就会对应一个实际最适深度与一个理论最适深度。

表2 进水COD浓度对应最适深度整合记录

图2 曲面数学模型
以X=200 mg/L为例,在曲面模型上对应Y=83 cm,Z=81 cm。代入图2中可算出Y′=82.7 cm,Z′=82.3 cm。对比曲面模型的数据和拟合曲线的数据,两者结果相差不大,证明整个数学模型是准确有效的,实验是科学。该实验为CRI系统滤池高度的确定寻求了新方法。

