光热汽轮机低压进汽结构气动性能分析与优化设计

吴方松，邵卫东，李伯武，尹刚，宋立明，李军

(1.东方汽轮机有限公司，四川 德阳，618000；2.西安交通大学叶轮机械研究所，陕西 西安，710049；3.陕西省叶轮机械及动力装备工程实验室，陕西 西安，710049)

随着可再生化石能源的急剧减少和生态环境的持续恶化，新能源发电已经成为电力生产结构中的重要组成部分，其占有的比例将逐步升高。太阳能光热发电[1]作为新能源利用的一种新方式，具有分布广、易于储能等特点，从而成为了新能源商业化利用的重点方向。在太阳能光热发电系统中，汽轮机是将热能转化为机械能的关键动力设备，其机组效率直接影响系统的热效率。

低压缸的功率占整机功率的三分之一左右，故其效率也直接影响汽轮机组效率。尽管低压缸的叶片型线和叶片通道的优化设计已经相对完善，但目前低压缸的第一级效率只有65%左右，远低于其它级的效率[2]，导致整缸性能大幅降低。造成第一级效率严重偏低的原因可能有：级间漏汽损失[3]和无叶通道的低气动性能。级间漏汽未参与叶轮做功，直接流入级后并提高了级后温度，从而导致级效率降低，可通过调整级间密封来降低漏气损失。无叶通道是指主汽阀到凝汽器之间的所有连接管道和蜗壳，其气动性能主要包括总压损失和汽流组织形式等；无叶通道主要分为进汽和排汽结构，其中低压排汽缸的研究已相对成熟[4-5]。而在低压缸进汽道中，弯管和蜗壳造成的涡流损失和汽流组织不好，使得第一级的汽流入口均匀度和速比偏离叶片设计最佳值，这是导致第一级效率偏低的主要原因。

有研究者通过改变低压缸的进汽弯管[6]和导流片的倾斜角度[7]来提高进汽均匀度，从而改善第一级效率，但这种结构设计仅考虑了单独部件的气动性能，忽略了部件之间气动性能的相互影响[8]。从提高结构设计准确性的角度讲，需要将无叶通道与叶栅通道相匹配。

本文采用数值模拟对国内某太阳能光热发电汽轮机低压进汽结构进行通流分析，并对进汽蜗壳与弯管进行了优化设计，在此基础上研究了不同阀门结构设计对低压进汽结构气动性能的影响。

1 数值方法

1.1 计算模型

低压进汽结构由蒸汽阀、进汽弯管和蜗壳组成，在耦合第一级叶片的基础上，两部分共同构成了本文所采用的计算模型，如图1所示。蒸汽从进口进入蒸汽阀，再流过弯管后通过蜗壳，最后在叶栅中膨胀做功后从出口排出。考虑到第一级叶片与进汽蜗壳间的相互影响，本文采用整圈叶栅进行计算。为了更清晰地分辨出第一级叶栅结构，图2和图3分别展示了整圈静叶和整圈动叶，其中静叶与动叶的数目分别为42和146。整个进汽结构采用了轴对称布置的方式，且计算时的进口和出口都进行了相应的延伸来消除回流的不利影响。

图1 低压进汽结构模型

图2 低压缸第一级整圈静叶

图3 低压缸第一级整圈动叶

在计算模型经过光顺处理后，对图1所示的进汽结构进行了网格划分。进汽结构的网格由两部分组成：采用商业软件ANSYS-ICEM对无叶通道进行非结构化网格生成，采用NUMECA-AU-TOGRID对叶栅通道进行了六面体结构化网格生成。图4展示了蜗壳与弯管及其连接处的网格，在蜗壳出口与第一级静叶的交接面处网格布置较为致密。进汽阀的网格如图5所示，在曲率半径较小处也控制网格尺度与结构相匹配。考虑到边界层内速度梯度较大，对近壁面采用三棱柱网格进行了加密处理，如图6所示。生成的整圈静叶和动叶的局部网格如图7和图8所示，为了准确捕捉叶片表面的边界层和分离流动，对叶片表面均进行了加密处理。进汽结构整体网格的总节点数和单元数分别为1 700万和2 200万左右。

图4 蜗壳下部与进汽弯管表面网格

图5 蒸汽阀表面网格

图6 近壁面处加密的网格

图7 整圈静叶局部网格

图8 整圈动叶局部网格

1.2 边界条件

采用商业软件ANSYS-CFX对低压进汽结构进行数值模拟，该求解器基于有限体积法求解三维定常Reynolds-Averaged Navier-Stokes方程，具有二阶离散精度，同时采用了标准k-ε两方程湍流模型。计算采用的工质为可凝结水蒸汽Steam5V；进口给定总压和总焓为1.565 MPa和3 214.1 kJ/kg，出口给定静压为1.27 MPa；固体壁面采用绝热无滑移边界条件。在各项残差收敛到10－5时认为计算收敛，通过调整壁面网格分布来达到湍流模型对Y+的要求，本文计算得到的Y+分布如图9所示，满足标准k-ε湍流模型的要求。通过与实验流量对比，本文数值计算的流量相对误差为0.022%，进一步证实了本文所采用的数值方法的有效性和准确性。

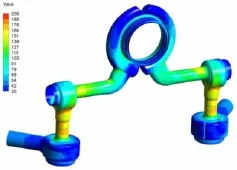
图9 低压进汽结构的Y+分布

2 结果与讨论

2.1 低压进汽结构的优化设计

在对低压进汽结构进行优化设计之前，先对原始结构进行通流分析。图10给出了进汽弯管与蜗壳内流线分布，整体分布成轴对称性，在弯管内流线分布较为均匀且速度大小基本相等；在蜗壳内流体从蜗壳下部沿着壁面流到蜗壳上部，并且速度分布呈现上部速度低而下部速度高的特点。但是在弯管与蜗壳连接处有两个滞止涡 （图10中红色标记所示），这是从弯管流出的部分流体撞击到蜗壳壁面所造成的。这两个滞止涡会减小蜗壳内流体的通过面积，阻碍流动并增加一定的压力损失。

图10 进汽弯管与蜗壳内流线分布

原始进汽结构的弯管与蜗壳连接不仅会直接影响蜗壳内的流动，还会间接影响蜗壳第一级静叶的进汽均匀度和汽流角。为了定量描述这种间接的影响，给出了叶栅通道内三个速度分量 （径向速度RV、轴向速度AV和周向速度TV）和汽流角α的定义，切向速度以逆时针方向为正，如图11所示。选取蜗壳与静叶域的交接面上 （如图1中P3位置所示）的速度分量和汽流角作为目标函数，因为位置P3既能反映静叶的进口汽流角也能反映蜗壳与第一级的相互作用。

图11 叶栅通道内速度分量与汽流角示意图

图12给出了蜗壳与静叶交接面P3上的轴向速度分量分布，面P3下部轴向速度较大而上部轴向速度较小；从进汽弯管出来的流体经过蜗壳收缩段加速导致下部轴向速度大，且图中虚线的指向正是进汽弯管的中心线方向。图13给出了面P3上的径向速度分布，其值相对于轴向速度较小且周向分布较为均匀。图14给出了面P3上的周向速度分布，左右两侧速度大小相同方向相反，这与蜗壳的对称性有关。图15给出了面P3上的汽流角分布，与周向速度分布的趋势相同，但是汽流角的跨度较大，这会造成第一级静叶的周向进汽攻角的跨度也较大，不利于叶栅通道中的汽流膨胀做功。

图12 蜗壳与静叶交接面上的轴向速度分布

图13 蜗壳与静叶交接面上的径向速度分布

图14 蜗壳与静叶交接面上的周向速度分布

图15 蜗壳与静叶交接面上的汽流角分布

为了进一步研究汽流角沿周向分布，选取叶栅通道10%、30%、50%、70%和90%等五个径向位置作为参考位置。图16给出了五个径向位置的汽流角周向分布，随着叶高的增大，汽流角逐渐减小；最大和最小汽流角分布在蜗壳的左右两侧，与汽流角分布云图一致。除了汽流角外，还需要考虑进汽不均匀度，并给出其定义：通过蜗壳与静叶域交接面P3上的流量与实验流量的相对误差。图17给出了蜗壳与静叶交接面上的进汽不均匀度分布，其呈现下部进汽多而上部进汽少的特点，与轴向速度分布的趋势一致。因此，从优化目标的角度看，对进汽弯管与蜗壳的改进主要是减小进汽攻角与进汽不均匀度。

图16 不同径向位置的汽流角周向分布

图17 蜗壳与静叶交接面上的进汽不均匀度分布

基于遗传算法的基本思想，每次保留对进汽攻角和进汽均匀度有利的几何调整，淘汰对优化目标不利的几何调整。经过若干次几何改进，给出了优化过程中产生的几个典型弯管与蜗壳连接结构，如图18所示。相对于原始结构，第一次优化时将弯管改为接近垂直方向，但弯管与蜗壳连接面积减少；第二次优化结构OP2在不改变弯管出流角度的基础上，增加了其与蜗壳连接处的出流面积；对于第三次优化结构OP3，既增大了弯管出流倾角，也增加了其出流面积。

图18 优化过程中的几个典型结构

优化的目标是改善静叶进口汽流攻角和进汽均匀度。图19给出了三种不同优化结构下蜗壳与静叶交接面上的汽流角分布，通过对比最大和最小汽流角发现优化后的结构满足OP3>OP2>OP1的关系。与图15中的原始结构汽流角分布对比可知，图19（a）中的汽流角的跨度更大，这说明减小弯管与蜗壳连接面积不利于组织汽流。从优化结构OP2和OP3得到的汽流角与原始结构对比可知，增大弯管出流面积和倾角有利于缩小汽流角的跨度。图20给出了三种不同优化结构下蜗壳与静叶交接面上的不均匀度分布，对比发现优化后的结构满足OP3>OP1>OP2的关系。与原始结构的进汽不均匀度（见图17）对比可知，三种优化结构均有较大的改善，也进一步说明增大弯管出流面积和倾角有利于改善进汽均匀度。将优化结构OP1和OP2得到的进汽不均匀度对比而知，增大弯管倾角更有利于静叶进口汽流的均匀性。

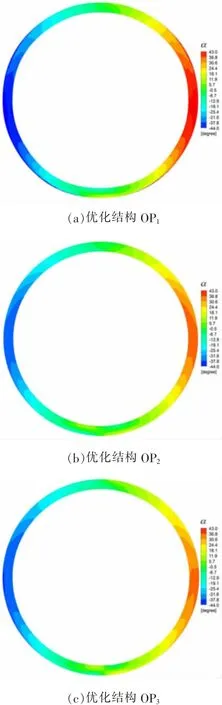
图19 三种不同优化结构下蜗壳与静叶交接面上的汽流角分布

图20 三种不同优化结构下蜗壳与静叶交接面上的进汽不均匀度分布

2.2 蒸汽阀对低压进汽结构气动性能的影响

在优化的弯管和蜗壳结构OP3的基础上，研究了蒸汽阀的偏心度对低压进汽结构气动性能的影响。图21给出了三种不同偏心度的蒸汽阀结构， 其中（a）为阀芯所处位置的截面， （b）、 （c）和（d）分别为偏心度为0 mm、20 mm和40 mm的蒸汽阀结构示意图。不同的偏心度不仅会改变阀门喉口处的通流面积，还会改变阀芯的类圆柱绕流涡脱落频率，对阀门的振动产生影响。对于后者的研究将会体现在后续的工作中，本文主要讨论偏心度对蒸汽阀气动性能的影响。

图21 不同偏心度的蒸汽阀结构

为了考查不同蒸汽阀偏心度对总压损失的影响， 定义总压损失系数为 φ＝1－Px／Pin， 其中 Pin为进口质量流量平均总压，Px为指定截面位置 （图1中P1、P2和P3）处的质量流量平均总压。图22给出了不同截面位置总压损失系数随偏心度的变化，随着偏心度的增大，总压损失系数逐渐减小。从图中还可以看出，不仅阀门会带来一定的总压损失，进汽弯管和蜗壳也会产生总压损失，但大部分总压损失仍是蒸汽阀造成的。

图22 不同截面位置总压损失系数随偏心度的变化

进一步分析不同偏心度下蒸汽阀的气动性能，图23给出了不同偏心度下蒸汽阀内的流线分布和速度云图。随着偏心度的增加，蒸汽阀中的最大速度和平均速度都相应地减小。这是因为偏心度的增大也会增加流入阀柱内的通流面积。由图可知，在偏心度为0 mm和20 mm的工况下，阀柱内的流线呈螺旋线式，这会导致相同流量下流体与阀柱的摩擦损失增加。在偏心度为40 mm的工况下，阀柱内的流线呈直线状，有利于通流并减小了总压损失。

图23 不同偏心度下蒸汽阀内的流线分布和速度云图

3 结论

本文基于三维RANS方程数值研究了国内某太阳能光热发电汽轮机低压进汽结构的气动性能。在对原始低压进汽结构通流分析的基础上，对弯管与蜗壳进行了优化设计，分析了优化结构改善汽流组织的机理；对比分析了不同偏心度的蒸汽阀结构对低压进汽结构的气动性能的影响，获得结论如下：

（1）结构的对称性决定了流场的对称性，原始低压进汽结构的静叶进汽角跨度很大，且最大值分布在蜗壳的左右两侧；

（2）增大进汽弯管的出流面积和倾角有利于减小进汽攻角和进汽不均匀度，优化的低压进汽结构OP3很大程度上改善了叶栅通道进汽的汽流组织；

（3）随着偏心度的增加，阀芯与阀柱间的通流面积增大，有利于汽流在阀柱内的通流并降低总压损失。