基于改进萤火虫聚类的异构WSNs能耗优化路由算法*
罗 剑,毕晓东
(浙江经济职业技术学院数字信息技术学院,杭州310018)
无线传感器网络(WSNs),是由随机投放在监测区域内的大量低成本且拥有传感、计算、数据处理和通信能力的微型节点构成的自组织网络,具有部署迅速、实时性强等优点。通过感知、收集和融合目标对象的观测数据,将预处理后的信息发送回基站,扩展了人们洞悉外部世界的能力[1-2]。根据节点计算能力、内存容量、通信带宽和初始能量等的差异,WSNs可以分为同构型WSNs和异构型WSNs。因为外界环境的制约,传感器节点通常由电池供电,自身携带能量有限,无法得到及时补充。仅初始能量不同的节点所组成的能量异构型WSNs在维持网络节点数量不变、降低成本开销的前提下增加了网络能量,特别具有研究价值[3]。
在传感器节点中动态均衡地分配通信和计算负载、从而节约能耗是WSNs路由算法需要解决的关键问题,很大程度决定了整个网络的生命周期[4-5]。分簇路由算法综合考量节点发送、接收数据的固定能耗和跟随传输距离远近改变的发送端无线功放能耗,将网络划分为若干本地簇,簇头消耗额外能量负责从簇成员接收数据并发往基站。分簇结构使得网络整体扩展性良好,相比节点与基站直接通信和节点间最小传输能量路由(MTE)性能更优,已经成为WSNs路由算法的研究重心,得到国内外学者的广泛关注[6]。LEACH算法是最早提出的WSNs分簇路由算法,利用合适的阈值概率公式,保持网络节点在运行周期内的各个轮次拥有同样的竞争簇头概率以平衡节点间能耗,但该算法只适用于节点初始能量相同的WSNs[7]。根据高级节点相对全体节点的数量占比和高级节点多于普通节点初始能量的比例,SEP算法修改阈值概率公式,按照初始能量的差异维持节点成比例地消耗能量,有效地延长了异构WSNs的稳定期(第1个节点死亡前)[8]。DEEC算法通过预测节点每个轮次的残余能量,修正不同节点竞争簇头的概率,比较SEP算法获得了更长的网络生命期[9]。
上述分布式随机分簇算法无须了解节点的具体位置,本地化自适应簇生成过程计算简单,减少了网络控制流量。然而随机算法存在两个问题:首先,每个轮次的簇头数围绕最优簇头数波动,加大了网络通信负载;其次,随机选择的簇头位置可能集中于局部区域,造成部分簇头与成员间距离过远,不利于平衡节点能耗。许多WSNs应用中节点位置预知,如果依据最优簇头数采用聚类算法获得更为紧密的本地簇,同时算法改进减少的网络能耗大于网络控制包负载和聚类计算的多余能耗,完全可能大幅度地提升网络能效。
萤火虫算法是一种仿生萤火虫个体的种群趋光性特征的群智能优化算法,起初用于求解非线性数值优化问题[10]。为了将该算法引入聚类分析领域,定义目标函数为聚类中心与簇成员间距离和,目标函数值越小萤火虫亮度越高。使用UCI机器学习库的13类典型基准数据集与其他11种聚类算法进行比较,结果表明萤火虫算法拥有良好的整体性能[11]。该算法进一步改善聚类效果、提高稳定性和降低计算负载的研究,围绕着萤火虫移动位置的选取策略和最优类中心扰动的快速收敛展开[12-13]。
综上所述,本文提出的IFCEER算法的基本思路是:WSNs初始化阶段节点将位置坐标一次性发往基站,使用改进萤火虫算法完成对全体高能节点的第1次聚类。随后运行的每个轮次分为簇形成和数据传输两个阶段。簇形成阶段向全网广播主副簇头消息,节点加入临近的簇。数据传输阶段簇头接收和融合成员数据,在事先规划指定的TDMA时隙发往基站。同时,该阶段根据阈值条件预测节点能量,决定是否重新执行聚类。因此,网络运行第1轮之后簇形成阶段只有在满足任意簇头能量小于指定阈值条件的轮次才会执行,否则保持原有簇结构。实验数据表明,提出的IFCEER算法平衡和降低了通信能耗,有效地延长了网络寿命。
1 系统模型
1.1 多级能量异构WSNs模型
考虑n个节点随机分布于M×M监测区域的多跳传感网络。假定S为网络内全体传感节点集合,如式(1)所示:
S={s1,…,si,…,sn}
(1)
式中,si表示第i个传感节点。
多级能量异构WSNs中节点初始能量在闭区间[E0,E0(1+αmax)]内随机分布,E0是节点能量下界,αmax决定了节点的最大能量。节点si的初始能量为E0(1+αi),其中αi∈[0,αmax]。因此,网络的整体能量可以描述为式(2):
(2)
模型具有以下特点:①基站位置固定于监测区域中心,能量和计算资源不受限制,通信范围覆盖整个监测区域。②节点拥有全网唯一的标识ID,位置固定。③基站通过某些渠道,如节点装备GPS等,了解每个节点的定位信息。④节点的发射功率以及通信半径可以根据需要自动调整。⑤链路对称,即已知发射端的发射功率,接收端可以根据接收到的信号强度估算两者距离。⑥节点以固定速率监测环境,定期上报监测数据。
1.2 能量消耗模型
本文采用文献[7]的能耗模型,即一阶无线电模型。发射方能耗ETX(l,d) 、接收方能耗ERX(l)和数据融合能耗Ec的具体公式如式(3)~式(5):
ETX(l,d) =ETX-elec(l)+ETX-amp(l,d)
(3)
ERX(l)=ETX-elec(l)=lEelec
(4)
Ec=lEDA
(5)
假定在一个轮次内每个簇成员发送l比特监测数据和自身残余能量等级到主簇头,因为残余能量占用数据位远小于l比特,所以忽略不计。主簇头将接收的全部信息融合成(1+φ)l比特信息包经副簇头发往基站。其中l比特是融合的本地监测数据,φl比特包含簇全体节点残余能量信息。根据前述能耗模型,得到每个轮次主簇头能耗EMCH、副簇头能耗EVCH和簇成员能耗EnonCH的相关公式如式(6)~式(8):
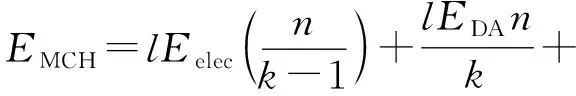

(6)

(7.1)
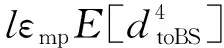
(7.2)
(8)
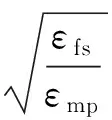
式中,k为簇数,dtoCH为簇成员与簇头间的平均距离,dtoBS为簇头与基站的平均距离,E[·]为期望值。由于簇头和基站间距离可能较远,式(7.1)对应自由空间模型,式(7.2)对应多路径衰减模型。假设节点满足均匀分布,则[8]:
(9)

(10)
式(10)是选择采用自由空间模型或者多路径衰减模型的依据,同理计算得到:
(11)
(12)
在一个轮次内簇消耗能量如下:
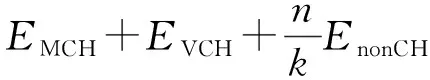
(13)
因为k≤n,所以一个轮次内网络消耗的全部能量Eround近似于:

(14.1)
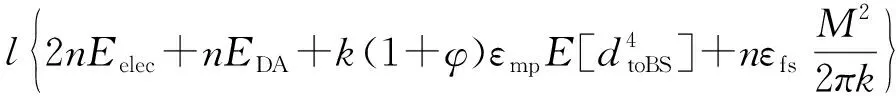
(14.2)
式(14.1)对应自由空间模型,式(14.2)对应多路径衰减模型,两公式分别对k求导数,得到不同模型下最优簇头数kopt公式如式(15.1)和(15.2)所示:
(15.1)
(15.2)
2 提出的IFCEER算法
2.1 改进萤火虫聚类


(16)


(17)
式中,nj是Gj中节点sj的个数。


(18)

亮度值的大小体现了萤火虫所处位置的优劣,目标函数值越小,萤火虫亮度越高。如果萤火虫F的亮度大于萤火虫Q,那么Q将被F吸引,即Q的kopt个分量一一对应地向F的kopt个分量所指示的方向移动。两个萤火虫分量的匹配规则是两两之间距离最近,假设Q中第i个分量qi与F的第j个分量fj之间距离rij小于与F的其他分量的距离,则qi向fj指示的方向移动。由于初始位置选取的随机性,两个萤火虫分量间的对应关系可能不具备充分的辨识度,如图1所示。萤火虫Q的#4分量与萤火虫F的#5分量距离更近,但是因为存在Q的#5分量,所以Q的#4分量只能和F的#4分量对应。当kopt增加时,这种随机匹配的概率同步增加。基于上述原因,算法依次从两个萤火虫的分量集合中查找距离最近的点对完成匹配,以维护合适的对应关系。
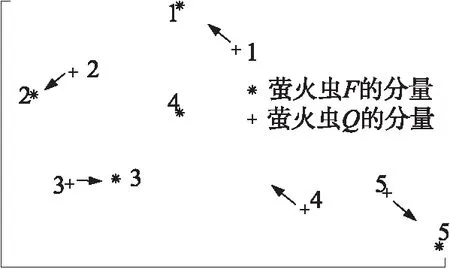
图1 萤火虫分量的对应关系
萤火虫彼此间吸引度公式为:
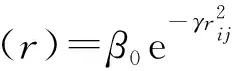
(19)
式中,β0为最大吸引度,γ为光强吸收系数。
萤火虫Q向F移动的位置更新公式如式(20)所示:
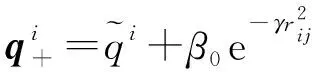
(20)
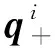
经过萤火虫之间互相吸引和移动之后得到的本次迭代最亮萤火虫,按照式(21)进行最优类中心扰动,评估再次移动效果。如果亮度优于移动前,则移动到新位置;否则保持原来位置不变。
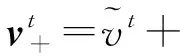
(21)
萤火虫算法的参数适用于标准化数据,所以需要对节点集合S进行标准化和归一化处理,标准化处理公式由式(22)列出:

(22)
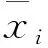
改进萤火虫聚类算法的主要步骤可以描述为:
步骤1 输入参数。传感节点集合S,最优聚类数Kopt,萤火虫群体规模N,最大吸引度β0,光强吸收系数γ,步长因子α,最大迭代次数τmax。
步骤2 根据式(22)标准化集合S;执行N次随机选择Kopt个节点作为萤火虫个体位置的操作,初始化全体萤火虫。
步骤3 由式(17)生成萤火虫各个分量对应的Kopt个聚类中心,根据式(16)计算萤火虫种群目标函数。
步骤4 将萤火虫按照亮度由低到高排序,从亮度最低的萤火虫开始两两比较,执行次数为N×N。如果Ii 步骤5 最亮萤火虫根据式(21)围绕其聚类中心扰动。如果得到的目标函数小于扰动前,则移动到新位置;否则保持原位置不变。 步骤6 达到最大迭代次数τmax停止算法,否则转到步骤3。 步骤7 输出最亮萤火虫V。 IFCEER算法支持周期性地远程监测WSNs,网络按照运行时序划分为若干轮次(round),每轮由两个部分组成:簇形成阶段和数据传输阶段,网络初始化还包括一个独立的信息收集阶段,如图2所示,T1≪T2。在每个轮次内产生分簇并传输数据,网络经历的轮次越多,说明网络运行时间越长,即网络寿命越大。 图2 IFCEER算法运行时序 2.2.1 信息收集阶段 (23) 参照式(15.1)或者式(15.2)确定最优簇数Kopt,对全体高能节点集合SHN运行改进萤火虫聚类算法,得到全局最优簇集合。 2.2.2 簇形成阶段 在每个簇中,选择距离簇聚类中心最近的节点作为簇内通信的主簇头(MCH),选择距离基站最近的节点作为与基站通信的副簇头(VCH)。主副簇头策略平衡了簇内负载,缩短了通信距离[15]。基站向全网广播簇头消息CH_stat_Msg(MCH_ID,VCH_ID),全体节点接收到该消息后,副簇头根据指定的主簇头加入簇,其他节点的入簇机制与LEACH算法相同[7]。 图3 IFCEER算法流程 2.2.3 数据传输阶段 (24) 因此,聚类只在当前簇头预测能量低于阈值Eth或者有节点死亡的少数轮次才会执行,从而尽可能地减少网络通信负载和计算延时,增强鲁棒性和适用性,IFCEER算法流程如图3所示。另外,一次聚类之后,没有采用在簇内高能节点间轮转(rotate)生成簇头来避免再次聚类的策略,主要基于三点考虑:①保留让外部节点加入网络的机会;②再次聚类可以动态寻找位置更优的簇头;③聚类计算由基站在时间充裕的数据传输阶段完成,鉴于基站强大的计算能力,不会影响网络整体性能。 为了评估IFCEER算法性能,使用MATLAB软件搭建仿真平台,完成两步实验。首先,分析改进萤火虫聚类算法的精度和收敛性;其次,从生命期、传输数据包、能耗、重新聚类次数占比等指标考量算法的网络性能。根据节点传输数据方式的不同设立了两组实验数据,分别是自由空间模型主导的100 m×100 m监测环境,以及多路径衰减模型主导的300 m×300 m监测环境,传感节点随机分布在监测区域。 聚类实验用于比较本文提出的改进萤火虫聚类算法IFA、萤火虫聚类算法FA和K-means聚类算法的性能指标[11,14],两种萤火虫算法的初始聚类中心保持一致,计算参数N=15,β0=1,γ=0.8,α=0.06。图4显示了在100 m×100 m数据集上3种算法聚类的收敛曲线,总迭代次数为20次,运行30次取平均值,得到IFA算法最优目标函数值JC=36.92,FA算法最优目标函数值JC=37.90,K-means算法最优目标函数值JC=39.21。因此,IFA算法的精度最高。IFA算法、FA算法和K-means算法达到最优目标函数值的平均迭代次数分别为9次、7次和16次。比较而言,K-means算法容易收敛于局部次优解,稳定性最差。IFA算法和FA算法收敛性基本一致,因为IFA算法引入了最优类中心扰动,所以迭代次数相比无扰动的FA算法略有增加。 图4 100 m×100 m数据集聚类收敛曲线 为了直观地对比聚类效果,图5中绘制了3种算法聚类后节点分布的隶属情况。图5(a)是IFA算法的簇结构图和聚类中心分布图,图5(b)是FA算法的簇结构图和聚类中心分布图,图5(c)是K-means算法的簇结构图和聚类中心分布图,图中O代表聚类中心。由图5可得,IFA算法簇划分更为均匀,簇内节点间的距离更接近,聚类效果优于其他两种算法。 图5 3种算法的聚类效果 网络实验在多级能量异构WSNs环境下比较IFCEER算法与DEEC算法性能。仿真实验参数如表1所示,其他参数与聚类实验相同。100 m×100 m监测环境的最优簇头数Kopt参照自由空间模型计算公式(15.1)得到;300 m×300 m监测环境的最优簇头数Kopt大于多路径衰减模型公式(15.2)的计算结果,是为了避免过多减少簇头使得簇内节点间距离增加甚至超过d0的情况大量出现。在网络稳定期,簇头数量等于最优簇头数Kopt;当节点大量死亡后,如果具备竞争簇头能力的高能节点的数量小于最优簇头数Kopt,则这些高能节点都成为簇头,以尽可能保持网络的连通。控制数据包携带了节点残余能量等级等信息。 表1 仿真参数 图6是存活节点图,反映了随时间关系网络中存活的节点个数。 图6 网络中剩余的存活节点数 图6(a)100 m×100 m监测环境 IFCEER 算法和DEEC算法分别在706轮和497轮出现节点死亡,在712轮和662轮有50%节点死亡,在716轮和775轮有90%节点死亡。图6(b)300 m×300 m监测环境IFCEER算法和DEEC算法分别在260轮和80轮出现节点死亡,在520轮和171轮有50%节点死亡,在548轮和442轮有90%节点死亡。可以看到,图6(a)中IFCEER算法的曲线几乎是一条垂直于y轴的直线。由于IFCEER算法引入了预测能量阈值,只有大于该阈值的高能节点具备竞争簇头的资格,网络能耗被均匀地分布到异构网的每个节点上,因此第1个节点和最后一个节点的死亡时间非常接近。图6(b)300 m×300 m监测环境簇内节点间距离大幅增加,副簇头与基站平均距离大于d0,可以反映算法在恶劣条件下的性能表现。IFCEER算法大部分节点在450轮之后才开始死亡,而DEEC算法在80轮之后节点就迅速死亡,网络性能下降严重。体现出改进萤火虫聚类对比随机聚类在寻找紧密簇结构、生成全局最优簇方面的优越性,而且主副簇头机制进一步均衡了网络能耗。从图6可以看到,与DEEC算法比较第1个节点死亡时间,IFCEER算法在100 m×100 m和300 m×300 m监测环境使得网络寿命分别提高了43%和225%。更长的网络生命期意味着更多的传输数据,如图7所示,DEEC算法在100 m×100 m监测环境网络整体传输了67 231个数据包,在300 m×300 m监测环境传输了23 923个数据包;而IFCEER算法分别为75 026和51 769,效果提升明显。 图8展示了网络总体能量随时间的消耗情况。两组实验环境中IFCEER算法网络生命期能耗曲线的斜率几乎保持不变,均低于DEEC算法的能耗曲线,IFCEER算法的性能表现为更节约能量。 图7 网络传输的数据量 图8 网络总体能耗 由表1可知,自由空间模型100 m×100 m监测环境的能量消耗中接收和发送数据的电路固定能耗占比较大,因此IFCEER算法的优势更多地体现在节点间能耗的均匀分配,从而推迟节点的平均死亡时间。多路径衰减模型300 m×300 m监测环境的消耗能量中随传输距离改变的无线功放能耗占据主导地位,造成经过全局最优聚类获得紧密簇结构的IFCEER算法的能耗显著低于DEEC算法。表2是两种算法的能耗统计,与经典DEEC算法相比,随着节点间传输距离的增加,本文采用的IFCEER算法有效减少了网络的总体能量消耗,网络性能得到了很大的提高。 表2 两种算法的能耗统计 根据式(24),通过比较全体簇头的下一轮预测残余能量与阈值能量的大小决定网络运行过程是否重新聚类,簇形成阶段执行的次数与重新聚类的次数相当。因此,重新聚类次数越少,网络通信负载越低。IFCEER算法默认有节点死亡的轮次都会重新聚类,所以仅统计网络稳定期所有轮次对应的重新聚类次数。仿真运行20次得到的100 m×100 m监测环境数据如表3,结果表明只有约29.5%的轮次需要重新聚类,有效地减少了网络控制包数量。 表3 IFCEER算法重新聚类次数 本文提出基于改进萤火虫聚类的异构WSNs能耗优化路由算法IFCEER,算法通过改进萤火虫聚类算法对全体高能节点进行预测分簇,在簇内选择与聚类中心和基站临近的高能节点作为主副簇头,形成结构紧密的全局最优簇集合,只有大于指定残余能量阈值的节点具备持续竞争簇头的资格。利用上述策略,较好地平衡了网络的能量负载,降低了网络能耗,从而达到延长网络生命期的效果,仿真实验证明IFCEER算法拥有可观的性能提升。后续研究围绕3个方面开展:①综合节点距离、残余能量等因素拓宽萤火虫聚类算法中目标函数的定义,使得聚类结果更深刻地反映网络变化情况,简化后续执行步骤;②在节点死亡后动态增加新节点可以持续保持网络的通信能力[16],注入新节点的策略值得深入研究;③大规模WSNs基站和簇头相距遥远,需要采用簇间多跳方式解决远距离数据传输问题。利用IFCEER算法为基础,开发相应的新算法是可行之道。2.2 算法实现


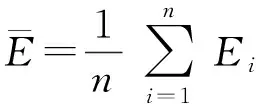

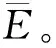
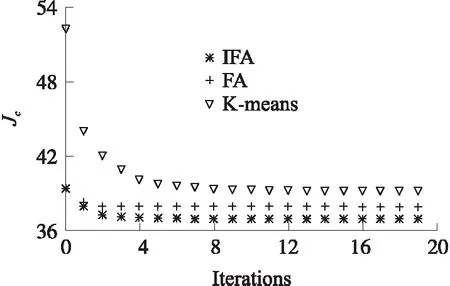
3 仿真与结果分析
3.1 聚类仿真实验
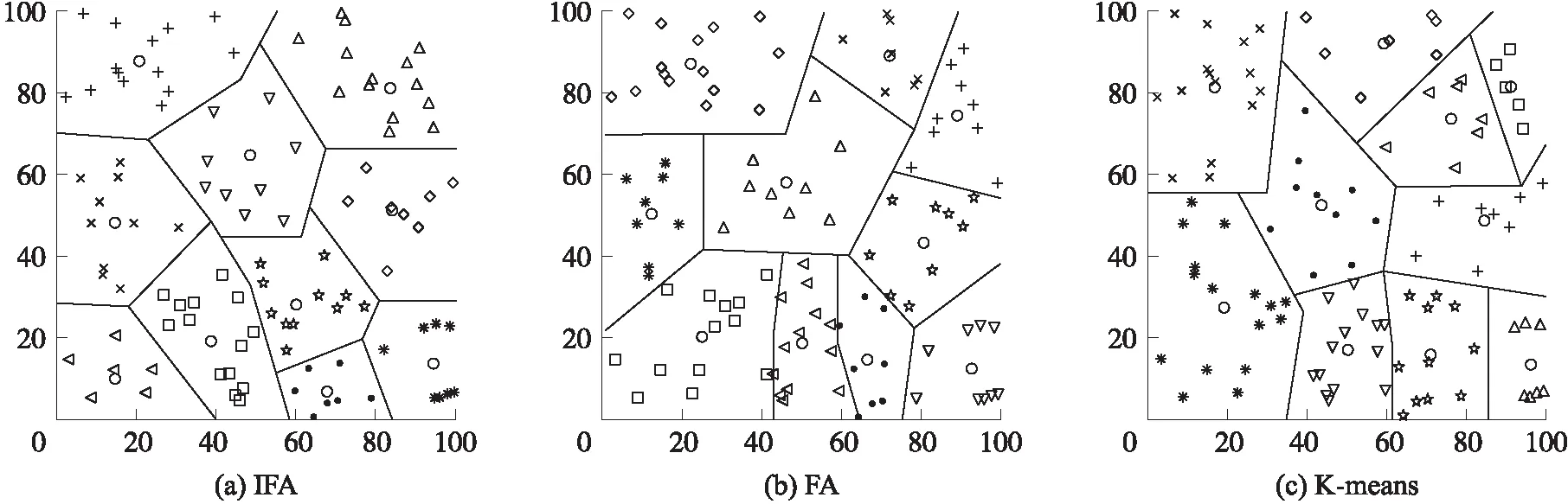
3.2 网络仿真实验


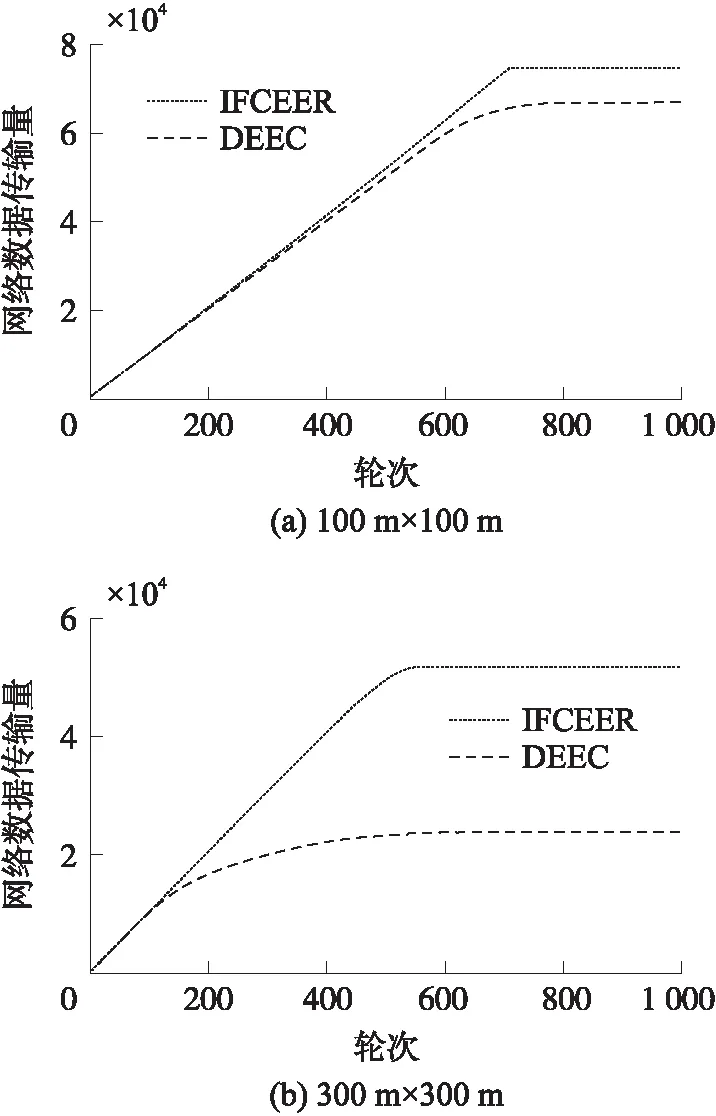
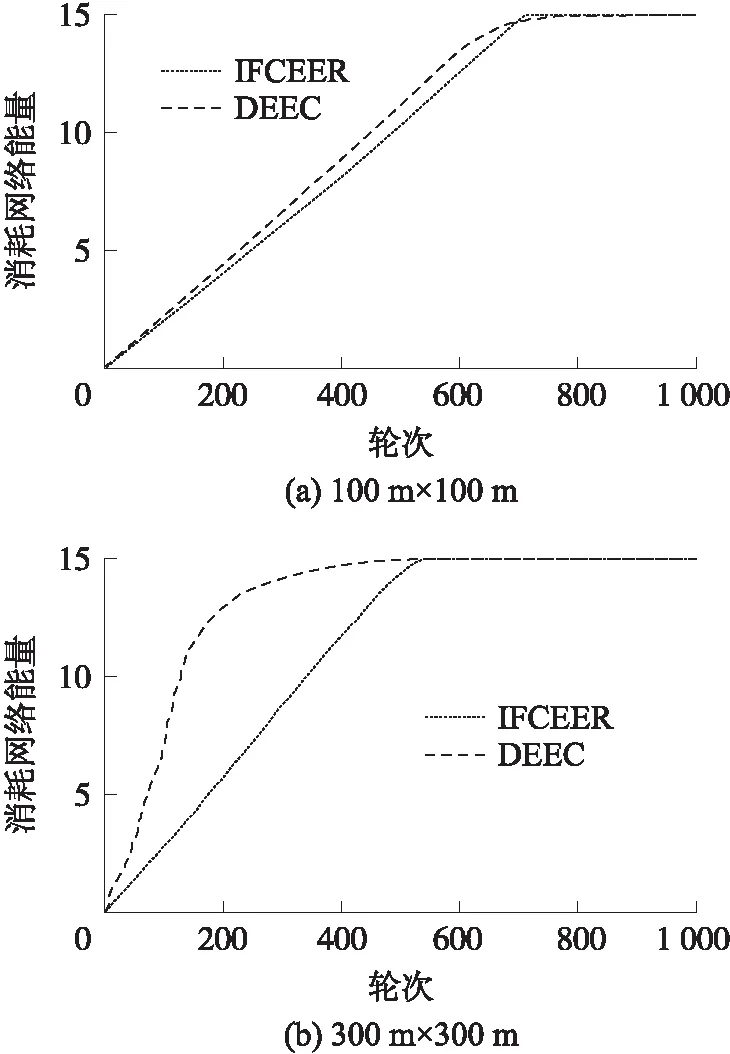


4 结束语

