Development of nonlinear disturbance observer based control and nonlinear PID:A personal note

Wen-Hua CHEN

Department of Aeronautical and Automotive Engineering Loughborough University,Loughborough,Leicestershire LE11 3TU,U.K.

Received 3 July 2018;revised 31 August 2018;accepted 4 September 2018

Abstract

This paper gives an overview of early development of nonlinear disturbance observer design technique and the disturbance observer based control(DOBC)design.Some critical points raised in the development of the methods have been reviewed and discussed which are still relevant for many researchers or practitioners who are interested in this method.The review is followed by the development of a new type of nonlinear PID controller for a robotic manipulator and its experimental tests.It is shown that,under a number of assumptions,the DOBC consisting of a predictive control method and a nonlinear disturbance observer could reduce to a nonlinear PID with special features.Experimental results show that,compared with the predictive control method,the developed controller significantly improves performance robustness against uncertainty and friction.This paper may trigger further research and interests in the development of DOBC and related methods,and building up more understanding between this group of control methods with comparable ones(particularly control methods with integral action).

Keywords:Disturbance observer,nonlinear control,PID controller,disturbance observer based control

1 Introduction

Disturbance observer based control(DOBC)is now a well known control method and has found a wide range of applications.The objective of this paper is twofold:one is to provide a review of the history of the development of a nonlinear disturbance observer technique and a nonlinear DOBC design[1]and the other is to present a piece of the work about the link between DOBC and nonlinear PID for a robotic manipulatorunder a number of assumptions.A specific nonlinear disturbance observer technique of concern was developed in 1998 with papers published in[2]in 1999 and[3]in 2000.Actually before that,disturbance observers(DOB)have been developed and applied in a number of areas particularly in motion control[4,5].A few researchers attempts to extend this idea to nonlinear systems(e.g.,notably,[6]).This paper is not attempting to overview the disturbance observer based control and related methods.Researchers who are interested in this area please refer to several review papers[7,8].Instead,this paper is to provide a reflection of personal journey in the development of DOBC for nonlinear systems.20 years past since then and the method developed in 1998 are now attracting an even increasing interest from both academic and industrial community.However,in the first 10 years,this method was struggling to attract attention in the community particularly so called main streams in control theory and was quite difficult to get papers published.It is greatly appreciated for giving the author this opportunity to reflect this uneven journey.

On the other hand,there is always a strong interest in understanding the link between the controller with integral action and DOBC.The second part of the paper is devoted to this.Rather than developing a general understanding and insight of their relationship,a robotic manipulator is adopted as a case study to reveal their link.It will be shown that under a number of assumptions,the combination of a special nonlinear controller with a nonlinear disturbance observer may reduce to a nonlinear PID controller with all the gains being nonlinear functions of the states.The method employed in this paper is in the same fashion as that used in[2]where more general discussions between DOBC and PID have been studied and established.However,this result must not be over interpreted so concludes with a general statement that DOBC is equivalent to PID.In essence,DOBC is a two degrees of freedom control configuration while PID is a one degree of freedom control configuration.This work is also related to the very first work when motivating the research on nonlinear DOBC[3].It is quite suitable to present it together with the note of the history on this occasion.

This paper is organized as follows:Section 2 overviews the origin and the history of the nonlinear disturbance observer techniques.In Section3,the technical evolvement of the nonlinear disturbance observer and its related control strategy was described.Discussions will be provided on addressing and establishing properties of these methods.Section 4 is devoted to the link between DOBC and integral action for the special case of robotic manipulators.After the introduction of the dynamics of a robotic manipulator,a predictive control law was developed based on tracking performance.Then a nonlinear disturbance observer is designed to estimate friction and other unmodelled dynamics/disturbance.This nonlinear disturbance observer is integrated with the presented predictive controller together to form a DOBC scheme in Section 4.3.The stability of the composite controller is established.However the most significant and interesting contribution is to establish its link with nonlinear PID controllers.Then experimental results for the proposed controller are reported in Section 5 and the paper is ended with conclusions in Section 6.

2 Review of the origin of the nonlinear disturbance observer design technique

When employed as an EPSRC(Engineering and Physics Science Research Council)Postdoctoral Research Associate in the Department of Mechanical Engineering at University of Glasgow in 1998,Wen-Hua Chen was working on the development of nonlinear model predictive control(MPC)techniques for systems with fast and strong nonlinear dynamics.Traditionally MPC was originated from process industry where system dynamics are quite slow and in many cases could be reasonably appropriated by a linear system after being linearised around operational points.The slow dynamics in process industry allow computers with limited computing power to solve an online optimisation problem involved in MPC in real-time.Within the help of fast development of computing power,we were looking to develop MPC for mechanical and electrical systems(e.g.,robots and aircraft)where fast dynamics are involved in and in general nonlinearity of the systems to be controlled have to be taken into account.Hence the research focused on the development of fast MPC for systems with strong nonlinearity and fast dynamics.A novel nonlinear model predictive control scheme was proposed where no online optimisation is involved in as analytical solution was developed after several month hard work[9].In order to verify the proposed algorithm,it was implemented on a robotic manipulator that was directly driven by DC motors in the Department of Mechanical Engineering at the University of Glasgow.Despite promising performance in simulation,unsatisfactory tracking performance was observed in experimental tests.After calibrating all the parameters and examining all the possible causes,friction was identified as the main source of poor performance.A friction model was added to the controller to compensate this influence,and satisfactory performance was initially achieved.However,inconsistent performance was lately observed since friction changes with temperature,lubrication and other factors.This motivated Chen to develop a method that is able to directly estimate friction,rather than relying on a friction model whose parameters may change.Promising performance was demonstrated after implementing the proposed nonlinear disturbance observer on the robotic manipulator in the lab[3].

In preparing a paper to present this new design technique,it was found in the literature search that a similar concept was proposed by Ohnishi(1982)(e.g.,[10]and[11]).Motivated by the need of estimating unknown load torque in motor motion control,a transfer function based approach has been developed by Prof Ohnishi and his collaborators to estimate unknown load torque and then extended to a variety of applications.The technique was coined by Ohnishi as the disturbance observer or DOB.Although the design method and analysis tools in the DOB approach are completely different from Chen’s approach as DOB is based on transfer functions and frequency domain analysis and design techniques are only applicable to linear systems,the new technique was named as nonlinear disturbance observer technique and adopted in the title of the papers in[3].

Although friction can be considered as disturbance torque/force,it also could be considered as an outcome due to unmodelled friction dynamics.Encouraged by the very promising results observed in the experiments and simulations,Chen attempted to apply the same idea in estimating the influence of uncertainty,rather than external disturbance.Dynamic inversion control was widely regarded as one of the most promising techniques to deal with nonlinear dynamics in the aerospace control community.Nonlinear control dynamics are introduced to cancel the nonlinear dynamics of a controlled plant(so bear the name of dynamic inversion).But it also widely recognised that it may lack of robustness when real aircraft or missile dynamics are different from the dynamics model used to generating the dynamic inversion.This was a quite interesting and challenging topic.Inspired by the success in estimating of friction in robotic manipulators,the newly developed nonlinear disturbance observer technique was extended to estimate the change of missile nonlinear dynamics due to uncertainties in aerodynamics coefficients[12].Very promising performance was observed and robustness of the dynamic inversion control was significantly improved under significant changes of aerodynamic coefficients.Furthermore,it also showed that the nonlinear gain in the disturbance observer could provide a far better robustness than linear gains.In many design methods,strong robustness is achieved by the use of high gains or demanding high bandwidths.Careful study shows that the gains and the bandwidths of the proposed nonlinear disturbance observer are quitemodest.It shall be noted that both the external disturbance and the influence of the aerodynamic uncertainties were considered in this paper so this led to the concept of“lumped disturbances”.It was found out quite lately that this concept also appears in other techniques,most notably in Adaptive Disturbance Rejection Control(ADRC)proposed by Prof JQ Han(e.g.,see[13]and[14]).

The research in this area was boosted by the award of the first U.K.EPSRC grant in 2000,entitled“Disturbance Observer Based Control of Nonlinear Systems with Unknown Disturbances”to Wen-Hua Chen.The terminology Disturbance Observer Based Control or DOBC was formally proposed in the proposal.The specific schemes for the estimation of friction in robotic manipulators and the influence of aerodynamic uncertainties in missiles were then generalised into a systematic design method for dealing with generic nonlinear systems and a wide range of disturbances which now becomes the most widely used nonlinear disturbance observer design technique[1,7].A generic nonlinear Disturbance Observer Based Control(DOBC)framework was first proposed in[15],which provides a design procedure to integrate the proposed nonlinear disturbance observer with nonlinear controller design methods to form a composite controller with proven theoretical properties[15,16].With a continuous effort in the last decades by Chen and other researchers,a number of analysis tools and design processes have been established.The first book“Disturbance Observer Based Control:Methods and Applications”authored by him and his collaborators was published in 2014[1].Nonlinear DOBC work has been gradually attracting a considerable interest worldwide with a quite wide range of applications.To respond to increasing interests and research activities in DOBC and related methods,one special section on IEEE Transactions on Industrial Electronics and one special issue on the Transactions of Institute of Measurement and Control have been organised by Chen and his collaborators as in 2015 and 2016,respectively,as Guest Editors.

3 Nonlinear disturbance observer based control and discussion

There are basically two control strategies:feedback and feedforward.Feedforward can be used to compensate the influence of disturbances on output when they are measurable.Quite often,external disturbances are not measurable which significantly limits the applicability of the feedforward strategy.The basic idea of the disturbance observer concept is to design a mechanism to estimate unmeasurable disturbances.This very idea is similar to that in the widely used state observer design,where state observers are designed to estimate the state of a dynamics system and then the true state variables are replaced by their estimate in state feedback control design and implementation if they are not measurable.When the estimate yielded by the disturbance observer is integrated with the feed forward strategy,it constitutes the so calledDisturbance Observer Based Control(DOBC)which was named by Chen in the same fashion as widely usedState Observer Based Control.

3.1 The development of nonlinear disturbance observer technique

Next it will explain how the original idea of the nonlinear disturbance observer technique in[2]was inspired and developed.Consider a general nonlinear system described by

wherex∈Rn,u∈R andd∈R are the state vector,input and external disturbance respectively.It is assumed thatf(x),g1(x),g2(x)are smooth functions in terms ofx.

To estimate the unknown disturbanced,an intuitive update law of the disturbance observation would be like

As long as the above equation is stable in some sense(depending onl(x)),the error between the estimate of the disturbance,d,and the true disturbance,d,drives the the estimate to converge to the true disturbance.However the disturbancedis not available.

It follows from the original system dynamic(1)that

Therefore an intuitive disturbance observer could be constructed as

wherel(x)is the nonlinear gain function of the observer.

However,the above disturbance observer cannot be implemented since the derivative of the state is required.

Inspecting the above equation,it also could be written as

Letting

as an intermediate state variable andp(x)is a nonlinear variable to be decided.One has

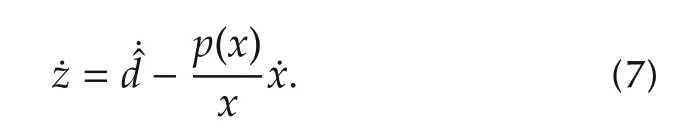
Therefore,a new nonlinear disturbance observer is then proposed after modifying the above basic observer,given by

wherez∈Rmis the internal state variables of the observer andp(x)∈Rmis a nonlinear function to be designed.The nonlinear observer gainl(x)is then determined by

It has been shown in[3]that the NDOB asymptotically estimates the disturbance if the observer gainl(x)is chosen such that

is asymptotically stable regardless ofxwhereed=d−dis the disturbance estimation error.

In the early days of the development,questions and criticism have been received from many aspects.Most of the criticisms have their own rights and demanded a better understanding of the properties of the proposed nonlinear observer and DOBC techniques.But it also made the early publication of any results in this area quite difficult,which was expected,to some extents,for any new technique.In the next few years,with the help of the U.K.government grant,significant progress in establishing their properties,developing design and analysis tools and extending to a much wider range of nonlinear systems and disturbances has been made.

3.2 Properties and further development

3.2.1 Performance under disturbances with bounded derivatives or of high frequency

The stability and convergence property of the proposed nonlinear disturbance observer(NDO)(8)was established under the assumption that the disturbance are slow time varying or unknown constant.However,in practical applications,external disturbances are quite complicated and could have many forms(may even changes from one type of disturbance to another).Hence they do not necessarily satisfy the slow-time varying assumption.Although the disturbance torque or force caused by friction is fast changing,both simulation and experiment results have confirmed that a promising performance in tracking non-slow time varying disturbance has been demonstrated.How to prove the stability of the disturbance observer does not destroy by high frequency component of general disturbances?This is not an issue for linear systems as external disturbance does not affect stability of the closed-loop systems.However this is in general not true for nonlinear systems.Rigorous analysis has been presented in[17],which shows that,as long as the change rate of the disturbance(i.e.the derivative of the disturbance)is bounded,the stability of the proposed NDO(8)stills holds.That is,under a mild condition,the estimate error of the disturbance is bounded under any disturbance with bounded derivative.Therefore the high frequency components in disturbance would not destroy the stability of the proposed nonlinear disturbance observer.This significantly extends the applicability of the proposed NDO and NDOBC.

It shall be highlighted that establishing the stability of the NDO in the presence of high-frequency components in disturbances does not imply the NDO shall be used to estimate disturbance of high frequency.It is quite often confused by many young researchers.In many times,it was asked whether or not the disturbance observer techniques could be used to estimate high frequency disturbance.The answer to this shall be negative.The reasons are as follows.First,most of the physical systems have inertia so the influence of high frequency components of disturbance on the output is much smaller as illustrated by the frequency response of a typical transfer function of a dynamic system.Therefore,the disturbance components of high frequency are naturally “filtered”out by the system dynamics.Secondly,in order to estimate the disturbance of high frequency,the bandwidth of the disturbance observer has to be quite high which not only may amplify high frequency noise of sensors,but also usually requires high observe gains.The latter may cause saturation problems on actuators and so called“peak phenomenon”in the transient period which may de-stabilise the whole closed-loop system.Thirdly,even if we are able to estimate disturbance of high frequency,normally actuators do not have an enough bandwidth(or fast enough)to implement the control command to counteract the high frequency disturbance.In summary,the disturbance observer techniques are mainly used for attenuating disturbances of low and medium frequency.It is NOT applicable/effective for attenuating disturbances of high frequency.Certainly high,medium or law frequency shall be interpreted in the context as there could mean different frequency ranges for different applications.

3.2.2 The existence and the choice of the nonlinear gain

The observer gainl(x)has to be chosen such that for anyx,the observer error dynamics(10)are asymptotically stable.There is a key question:does there exist such a nonlinear function l(x)which is also satisfies(9)such that the stability of the error dynamics holds regardless of x for any given nonlinear system?A related question is how to design such a nonlinear gain function if it does exist.To answer these two questions,[2]and[15]show that,as long as the relative degree from the disturbance to output is well defined,there does existl(x)such as the error dynamics(10)is stable regardless of the statex.That is,the nonlinear disturbance observer(8)converges to the true disturbance regardless of the statu of the statex.Furthermore,a systematic design method for the nonlinear observer gain is constructed and the convergence rate of the estimation could be adjusted by a tuning parameter.This not only sows the existence but also greatly simplifies the design of a nonlinear disturbance observer in the form of(8).

3.2.3 Separation of controller and disturbance observer design

In addition to its simplicity in its design,a most promising feature of the proposed disturbance observer design method and DOBC is that the controller design could be separated from the disturbance observer design.This somehow extends the so-called separation principle in state observer based design for linear systems into nonlinear systems.In the state observer based control design,a state feedback control law is designed under the assumption that all the state are available.If the state variables are not available,a state observer,e.g.,Luen berger observer or Kalman filter,is designed to estimate the state and the states in the control law are replaced by their measurements.It is shown that the state observer design can be separated from control design for linear systems under certain conditions.This is known as a separation principle,more formally known as a principle of separation of estimation and control.Due to the special feature of the proposed nonlinear systems in(8),the convergence of the observer does not depend on the state of the nonlinear systems.Therefore,the proposed NDO can be integrated with any nonlinear control design method to improve its disturbance rejection or/and robustness under certain conditions.In the design framework,a feed forward control strategy is first developed under the assumption that the disturbance is measurable,and then it is replaced by its estimate yielded by the disturbance observer.This realises theseparation principle but for nonlinear systems.It is believed that this very feature makes this specific DOBC design very attractive so becomes the most successful design method in this area.

4 Nonlinear PID for robotic manipulators

Another open question is what is the link between DOBC or related methods with controllers with integral action.As the disturbance observer based control technique can remove the steady state influence of disturbance on the output,it essentially achieves the“offset free”feature as the introduction of integral action.Actually an earliest work in this area by Johnson was motivated to develop a control method that could realises offset free under external unknown disturbance in the state space approach.In early 60’s,state space methods were rapidly developed and received a wide range of attention.External disturbance and model ling errors widely exist and it is quite easy to achieve zero steady state error by introducing an integral action.However,it was not clear how to realise this modern state space approach which significantly restricted the application of state space design methods.With the help of state estimation methods,by introducing unknown input observer concept,Prof Johnson proposed“Disturbance Accommodation Control”to address this problem[5,18].Therefore,a natural question is what is the link between DOBC and integral control such as PID.The relationship is not as simple and straightforward as someone might think.Obviously both of them are able to achieve zero steady state error under unknown constant disturbance or model ling uncertainty.More specifically,[2]has proved that by integrating a nonlinear disturbance observer with a nonlinear predictive controller,a DOBC can reduce to a nonlinear PI or PID controller depending on the relative degree of the nonlinear systems to be controlled.In the following,we further explore this relationship by investigating a specific case–a two link robotic manipulator.

4.1 Nonlinear predictive control

The dynamics of a two-link robotic manipulator can be described by a second order matrix equation,given by

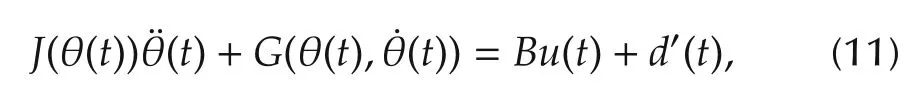
where θ∈R2,∈R2and∈R2denote the displacement,velocity and acceleration vectors of the robotic manipulator,respectively,u∈R2the vector of the generalized torque and/or force,d′the unknown exogenous disturbance vector andJ(θ) ∈R2×2the inertia matrix.G(θ)consists of Coriolis and centrifugal terms and the gravitational term,etc.In general,the matrixJ(θ)is positive definite for all allowable θ.When the first order dynamics of DC motors are included in the above model,uis the voltage vector imposed on the motors instead of the torque vector.In general the input matrixB∈R2×2is of full rank.For the sake of simplicity,the disturbanced′(t)∈R2is equivalent to the disturbancedon the control inputu(t)in this paper.Hence Equation(11)can be represented as

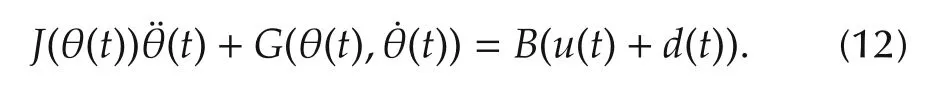
Suppose that the controlled outputy∈R2is the combination of the displacements of the robotic manipulator,i.e.,

whereC∈R2×2is a constant matrix of full rank and in many cases,Cis a unit matrix.

In the controller design,first it is supposed that there are no exogenous disturbances.In Section 4.2,we will discuss how to design a nonlinear observer to estimate the disturbancedand then compensate for it.

Model predictive control(MPC)performance index is adopted[9],given by

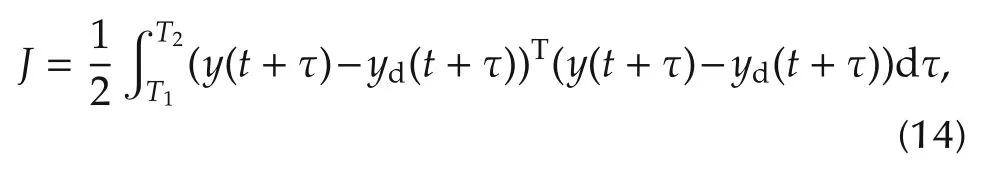
whereT1andT2are the minimum and maximum predictive times respectively.yd∈R2is the reference trajectory vector.

At time instantt,the future outputy(t+τ),τ ∈[T1,T2],is predicted using Taylor series expansion,which is a function of the current system statex(t)and future input in the time period[t,t+T2].Then a control profileu′(t+τ),τ ∈[0,T2]is generated by minimizing the tracking error performance index(14).However as in other receding horizon control algorithms,only the control action at time instanttis implemented,i.e.,

Then the above process is repeated as time goes.When the future output is predicted using Taylor expansion up to any order larger than or equal to 2,[9]showed that the model predictive controller can be given in a closed form.For the robotic manipulator(12)and(13)in the absence of disturbances,the nonlinear MPC law is given by

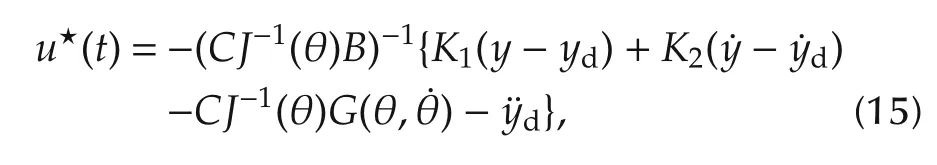
where the feedback gain matricesK1andK2are determined by

and

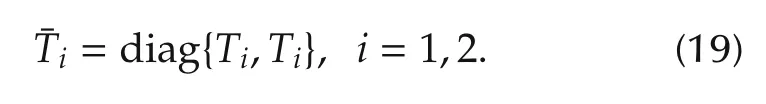
Note that the notation 0!=1 is used here.It is obvious that the gain matricesK1andK2depend on the choice of the predictive timesT1andT2explicitly.By adjusting these two design parameters,the desired system response can be achieved.[9]provides the criterion for choosing the design parameters in MPC based on overshoot and rising time specifications.Let the tracking error be defined by

Stability of the above nonlinear predictive control can be established by applying the stability results in[9]for the robotic manipulator(12).

Theorem1Suppose that reference trajectoryydand its derivativedare defined for allt≥0 and bounded.In the absence of exogenous disturbances,the closed loop system under the nonlinear predictive control(15)can exponentially track the desired referenceyd(t)for allt≥0.

4.2 Nonlinear disturbance observer

In Section 4.1,it is assumed that there are no disturbances.To compensate for the effect of the unknown exogenous disturbanced,a nonlinear disturbance observer is designed to estimate it.The nonlinear disturbance observer used in this paper is given by

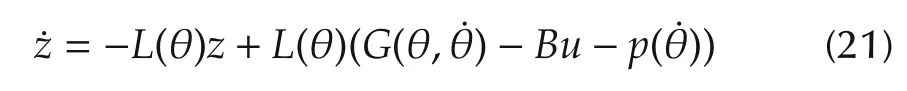
and

wherez∈R2andd∈R2are the observer state and the estimate of the disturbanced,respectively.The auxiliary variablep(˙θ)and the nonlinear observer gain matrixL(θ)are given by

and

respectively wherew1andw2are gains to be designed and

The convergence rate of this observer can be adjusted by the choice of the constantsw1andw2.

Stability of the above nonlinear disturbance observer is stated in Theorem 2 and the proof of Theorem 2 is given in the appendix.

Theorem 2For a two-link robotic manipulator(12)and(13)under unknown exogenous constant disturbances,the estimation yielded by the disturbance observer(21)and(22)converges to the disturbance exponentially,ifWin(25)satisfies

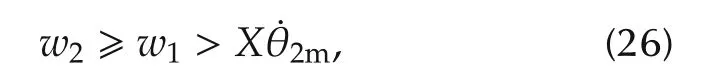
In order to develop the stability result,it is assumed that the disturbances are unknown constants.However,as shown in[3]and by experimental results in this paper,this assumption is not necessary in some cases(see further discussion in Section 5).

4.3 Nonlinear PID predictive controller

The control system diagram for robotic manipulators proposed in this paper is shown in Fig.1.The controller consists of two parts–the nonlinear predictive controller in Section 4.1 and the nonlinear disturbance observer in Section 4.2.In this and the following sections,we will investigate the properties of this control system scheme.It will be shown that this composite controller is equivalent to a nonlinear PID controller and stability of the composite controller will be established.

Fig.1 Robotic manipulator controller structure with the nonlinear disturbance observer.

When a disturbance is presented in the control input channel and measurable,a simple feed forward strategy can be adopted.A combined feedback and feed forward configuration is given by

whereu(t)∗anddare given by the nonlinear MPC(15)and the true disturbance is replaced by its estimate given by the the nonlinear disturbance observer(21)and(22).The control configuration diagram is shown in Fig.1.

It follows form(22)–(24)that

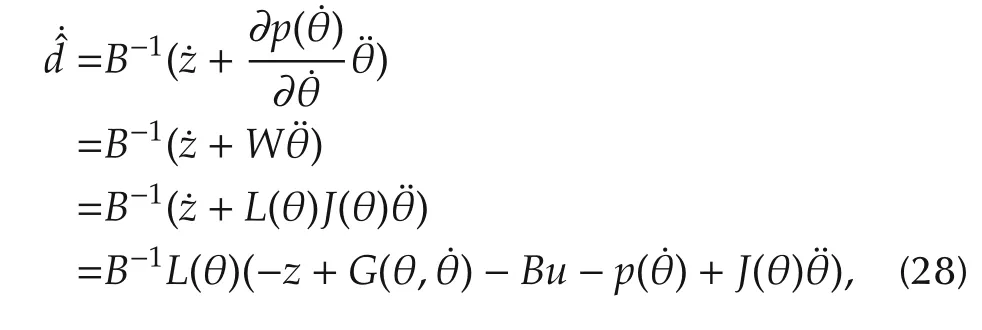
where the last equality follows form the nonlinear observer equation(21).

Invoking(22)and the nonlinear MPC(15)and(27)into(28)gives

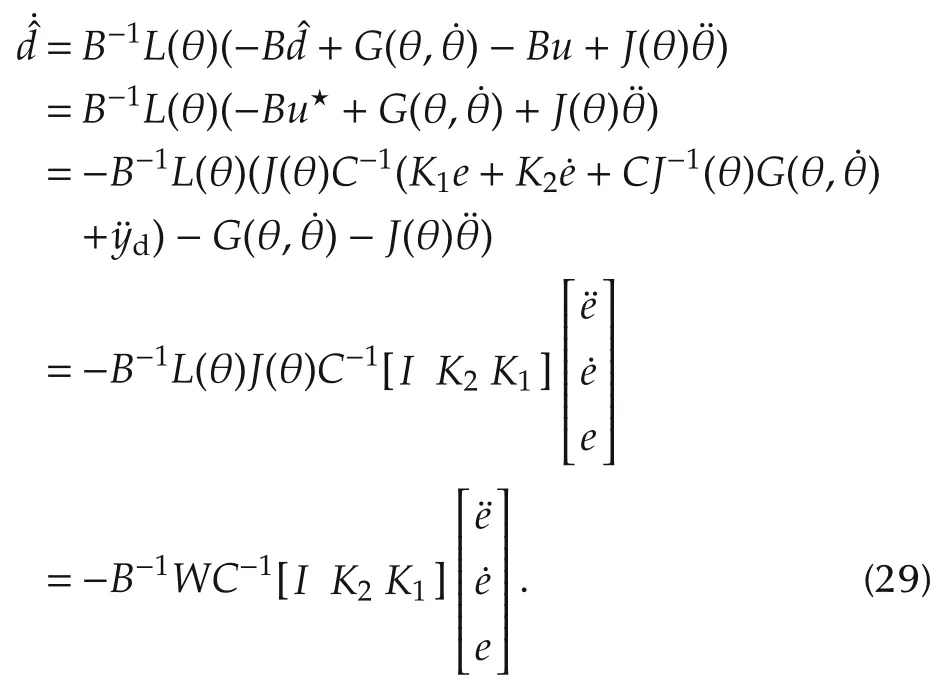
Integration of(29)from the initial time 0 totyields

When the initial disturbance estimate is chosen as

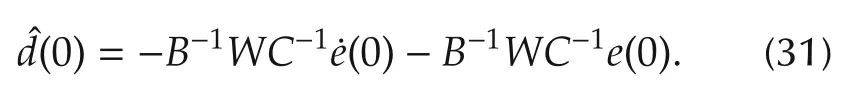
Equation(30)becomes

Then substituting the disturbance estimate(32)and the nonlinear MPC(15)into the control law(27)yields

This composite controller can be further written in the PID controller structure,given by

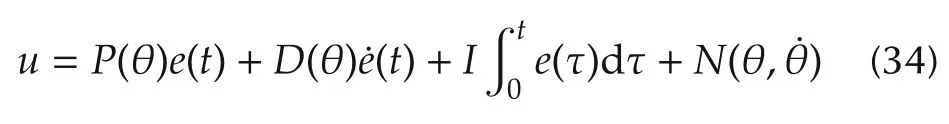
with the proportional gain

the derivative gain

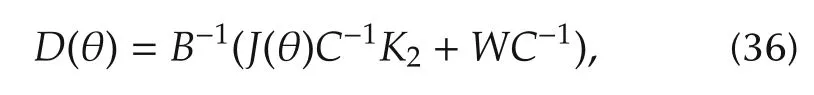
the integral gain

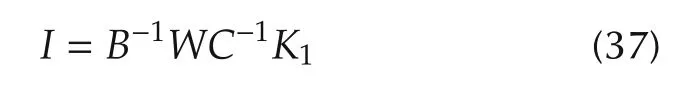
and

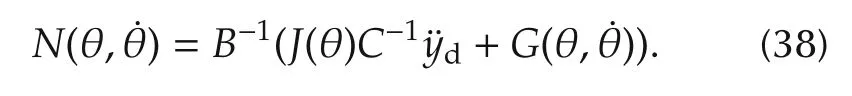
This controller is referred to as anonlinear PID predictive controlleras shown in Fig.2 wherexdenotes the state vector of the robotic manipulator,i.e.,x=[θ;].

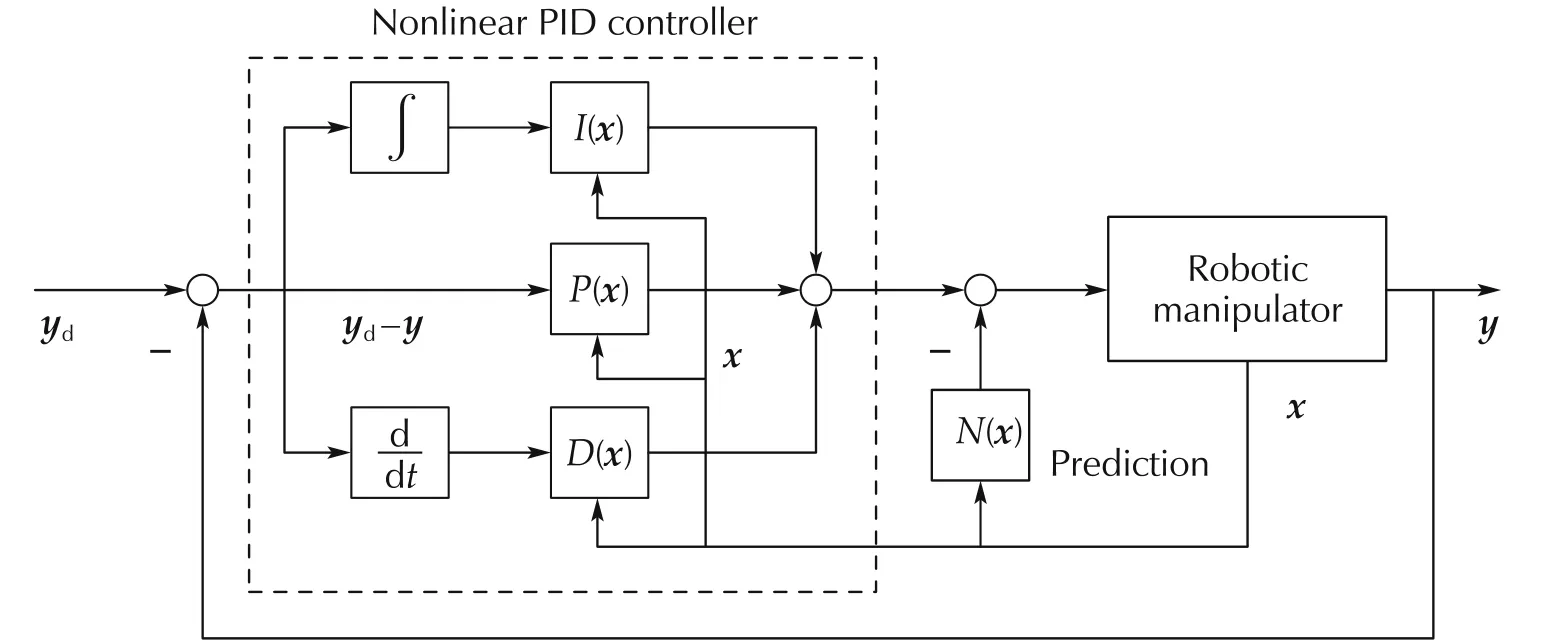
Fig.2 Nonlinear PID predictive controller.

The proportional and direvative coefficients are nonlinear functions of the displacements of the links θ.In addition to the traditional PID structure,a prediction partN(x)(see(28))is included in this controller.It consists of two terms.The first termB−1J(θ)C−1takes into account the control input requirement for future output using the second order derivative of the reference signal(note that the first derivative of the reference is employed by the PID part.)The latter termB−1G(θ,˙θ)is to make up the influence of the current system’s dynamics on future output.HenceN(x)takes into account the influence of the current system’s dynamics on future output and the input requirement for tracking future reference.This can be explained from the fact that this controller is derived from the predictive control method in Section 4.1.

4.4 Stability

Stability is essential for a control system.It is important to investigate stability of the composite controller consisting of the nonlinear predictive control(15)and the nonlinear disturbance observer(21)and(22).

Define the observer error as

Since it is assumed that the disturbances are unknown constant,it follows from the observer(21),(22)and the system model(12)that

Furthermore substituting the control law(27)into the manipulator dynamics yields

Invoking(15)into(41)together with(40)yields the the closed-loop error dynamics of the robotic manipulator under the composite controller,given by

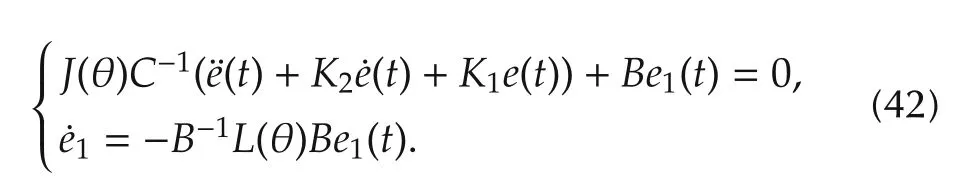
Theorem 3Consider the two-link robotic manipulator(12)and(13)with unknown exogenous constant disturbances.Suppose thatydanddare defined and bounded fort≥0.The two-link robotic manipulator under the composite controller consisting of the nonlinear MPC(15)and the nonlinear disturbance observer(21),(22)as in Fig.1,i.e.,the nonlinear PID predictive controller(34),exponentially tracks the reference trajectoryydif the condition(26)is satisfied.

The proof of the above stability result is given in the appendix.

Remark 1Theorem 3 states that as long as the maximum velocity of the second link,i.e.,˙θ2m,satisfies condition(26),the robotic manipulator under the nonlinear PID controller developed in this paper can track the reference trajectoryydin the presence of unknown constant disturbances.It can be shown that the maximum velocity of the robotic manipulators depends on the maximum velocity of the reference trajectory,the initial position and velocity error between the robotic manipulator and the reference,and the disturbances imposed on the robotic manipulator.This is easy to understand from physical properties of the robotic manipulator.In particular,when there is no initial error between the position and velocity of the robotic manipulator and the reference,the bound of the maximum velocity only depends on the maximum velocity of the reference trajectory and the size of the disturbances.

5 Experimental results

5.1 Experiment setting

The proposed nonlinear PID predictive control is implemented on a two-link horizontal robotic manipulator in the laboratory.The experiment layout is shown in Fig.3.In this experiment,a direct drive motor is attached to each joint and potentiometers and tachometer are mounted at the end of each link to measure the position and the velocity of the links.Since the outputs of the tachometers are quite noisy,the signals from the tachometers are filtered by digital filters before used to calculate the control action.The motor dynamics are approximately represented by a first order model.The definitions of the position and its direction of two links are given in Fig.4.

Fig.3 System layout of the experiment.

Fig.4 A two link robotic manipulator.

All the calculation in the nonlinear controller and the nonlinear disturbance observer is performed by dSPACE.The physical data and parameters of this system are given in the table of the appendix.Two controllers are implemented and compared.One is the MPC without disturbance observer and the other the nonlinear PID predictive controller proposed in this paper(e.g.,the combination of MPC with the nonlinear disturbance).

5.2 Experimental results

The experimental results for MPC and the proposed nonlinear PID predictive controller are shown in Figs.5 and 6,respectively,which are directly taken from dSPACE trace window.In both Figs.5 and 6,the first column and the second column are for the first link and the second link respectively,and the motor inputui(V),velocity((°)·s−1),displacement θi(°)and reference signalydi(°)are displayed in the order from the top to the bottom.The reference signal for each link is generated by the output of a stable transfer functionGr(s)driven by a pulse generator with the amplitude 90 degree.The transfer functionGr(s)can be considered as a desired model that the robotic manipulator should follow.It represents the tracking performance specifications and is chosen as

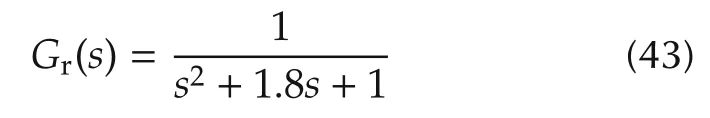
for the both links in the experiment.It is obvious that the reference signal generated by the above model driven by a pulse generator is smooth and differentiable up to second order.

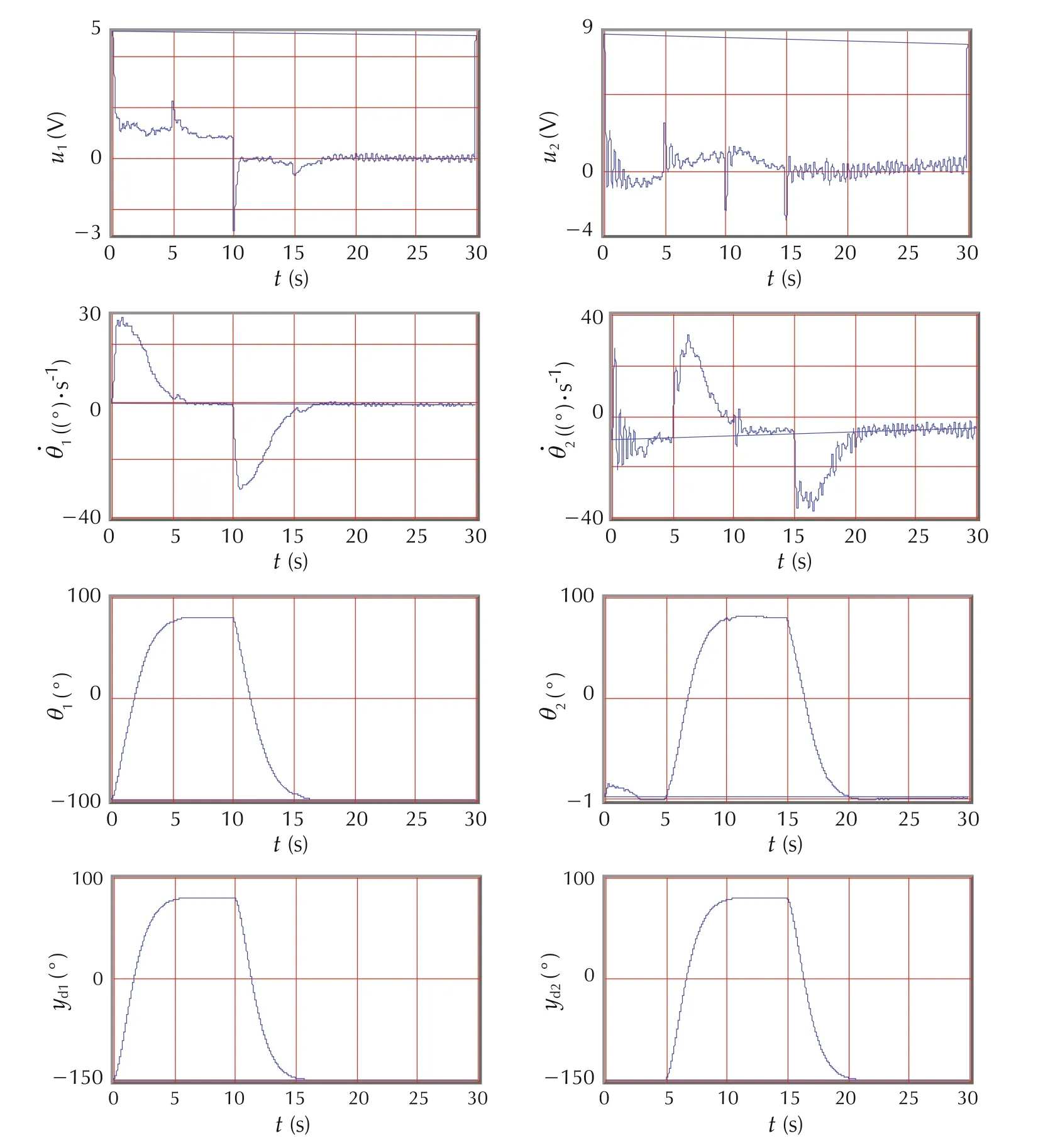
Fig.5 Experimental result of Nonlinear PID predictive controller Vi:the velocity of ith link;Pi:the position of ith link.

Fig.6 Experimental result of model predictive control without disturbance observers.

In the MPC,the predictive times in the performance index(14)are chosen asT1=0 andT2=1/1.2s and used in(15).The nonlinear PID predictive control uses the same parameters but with a a disturbance observer and its observer gains are selected as

The tracking performances of the proposed nonlinear PID predictive control and the MPC are further compared in Figs.7 and 8.The nonlinear PID controller significantly improves the tracking performance.There are two important factors degrading the performance of the MPC in this experiment.One is friction and the other is the mismatch between the model used for the controller design and the real robotic manipulator.

For the nonlinear PID predictive controller,since it is derived from integration of the nonlinear predictive controller and the nonlinear disturbance observer,the observer considers the disturbance torque caused by the friction as a part of disturbances and estimates and then compensates for it.The tracking performance in Figs.7 and 8 shows that the nonlinear PID predictive controller works well against friction.The tracking error in state steady is removed.

In model ling the two-link robotic manipulator,the effects of the sensors,connection,wire,etc,are ignored.The controller is directly generated based on the dynamic model of the robotic manipulator and the physical parameters in the table of the appendix.Due to the mismatch between the model and the real robotic manipulator,the coupling effect between the two links cannot be completely removed by MPC and this is evident by the fact in Figs.7 and 8.

Fig.7 Nonlinear PID predictive controller versus computed torque control:First link.

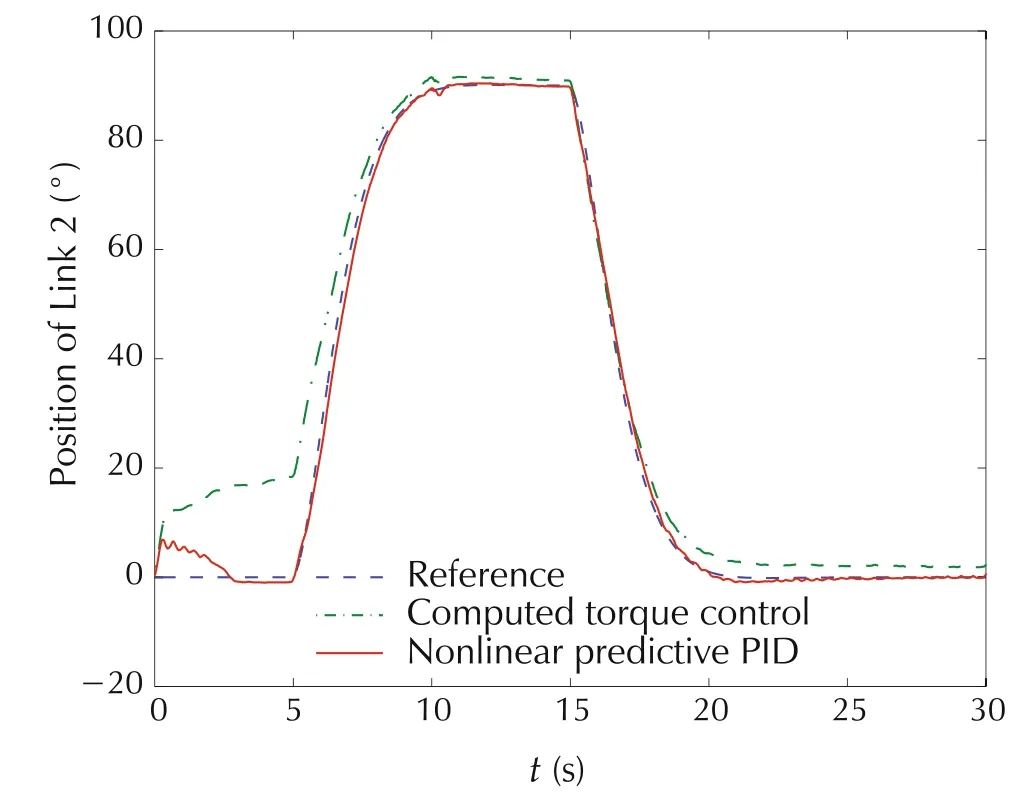
Fig.8 Nonlinear PID predictive controller versus computed torque control:Second link.

At the beginning of the experiment,the first link moves to track the reference signal.It is required that the second link maintains the relative degree between the first link and the second link to be zero during the period 0–5s.However,Fig.8 shows that for MPC the second link has significant tracking error.In the proposed nonlinear PID predictive controller,the remaining coupling effect due to the unmodelled dynamics is considered as an unknown disturbance,and the built-in disturbance observer estimates and then compensates for it.The similar phenomenon occurs at 5s when the second link starts to track its reference trajectory.As shown in Fig.7,compared with the MPC,the nonlinear PID predictive controller greatly reduces the tracking error of the first link caused by the coupling effect.This is clearly evident that the nonlinear PID controller exhibits quite good performance robustness.

6 Conclusions

This paper provides a history account of the development of the nonlinear disturbance observer.It starts from the motivation,the intuitive idea of the technical development and the original disturbance observer design method,and then presents the criticism it has received and the features of the DOBC method.The simplicity of its design and the separation of the disturbance observer from control design are two most attractive features.In this sense,it is very similar to widely used Lunegerber observer or Kalman filter techniques.Certainly there may be still a room to further improve the deign and analysis methods.Hopefully,with all the effort,it will eventually become a powerful tool for engineers and as widely popular and used as state observer design techniques.

Then the paper focuses on a special aspect of the proposed method and tries to build up more understanding between the DOBC approach and controllers with integral action.To this case,rather than trying to answer this question in a generic sense,it chooses the very first case study that motivated the development of the nonlinear disturbance observer design technique–a two link robotic manipulator to investigate their relationship.A predictive controller is firstly designed using a tracking performance index and the a nonlinear disturbance observer is designed for the two link manipulator.By carefully choosing the initial state of the nonlinear observer and the observer gain function,it is shown that the combination of the nonlinear predictive controller with a disturbance observer under these special choices actually reduces to a nonlinear PID controller.However it shall be noticed that this conclusion holds only under a number of assumptions:a specific nonlinear baseline controller,a specific choice of the nonlinear observer gain and the specific choice of the initial estimate of the disturbance.On the other side,there are some significant differences between these two methods.First,DOBC is a two degrees of freedom control configuration with both a baseline controller and an addon disturbance observer while a controller with integral action(e.g.,PID)is one degree of freedom control configura-tion.Secondly,integral action in a controller affects both regulation/tracking and disturbance attenuation performance while a disturbance observer mainly affects disturbance attenuation and robustness gainst uncertainty.For example,when a set point changes,the integral action will kick in and cause overshoot.But the disturbance observer loop is not active in the presence of the change of a set point.More research shall be carried out in understanding the relationship between these two types of control mechanisms.

Appendix

Proof of Theorem 2The proof is modified from the proof of Theorem in[3].The main difference is that the different observer gains are allowable for different links in Theorem 2.

First letd′=Bdand,following(22),its estimate is given by

wherezandp(˙θ)are given by(21)and(23)respectively.It is obvious that in order to prove stability of the observer(21)and(22)ford,it suffices to prove that the observer ford′is exponentially stable.

Sincep(˙θ)is given by(23),we have

Let

It follows form(21),(a1),(a2)and(24)that

Invoking(12)into the above equation yields

Hence the estimate error ofd′is governed by

The inertial matrixJ(θ)for a two-link manipulator is given by[19]

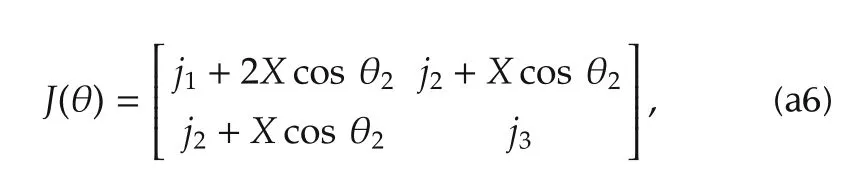
wherej1,j2,j3andXare inertial parameters which depend on the masses of the links,motors and tip load and the lengths of the links.

A candidate Lyapunov function for the observer(21)and(a1)is chosen as

Differentiating the Lyapunov function with respect to timetalong the observer trajectory gives

That is,

which can be further rewritten as

Sincew1andw2satisfy(26),this implies

and

Hence the inequality(54)is met.Since the Lyapunov function(51)is positive definite and its derivative along the trajectory is negative if condition(26)is met,this implies that the system approaches to the equilibrium(e′=0)exponentially.Therefore the estimation yielded by the disturbance observer converges to the disturbances exponentially. □

Proof of Theorem

3Let

whereeis the tracking error andits derivative of the tracking error.The first error equation in(42)can be written as

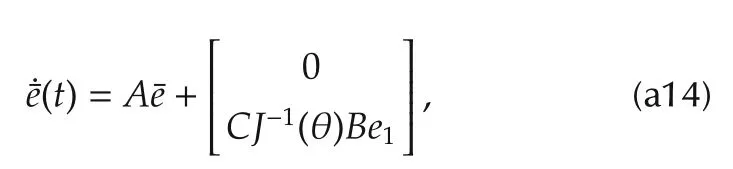
where

and

Define a candidate Lyapunov function asV(ē)=ēTPēwherePis given by the Lyapunov equation

andQis a positive definite matrix.In the absence of the observer errore1,the error dynamics of the closed-loop system(a14)reduces to=A.Theorem 1 implies that the matrixAin(a15)is stable.Thus it can be shown thatPis positive definite whenQis positive definite.

The derivative of the Lyapunov function with respect to timetassociated with the system(42)is given by

where λmin(·)denotes the minimum eigenvalue of a matrix and‖·‖denotes the Euclidean norm of a vector and the induced Euclidean norm for a matrix.c1is a constant defined by

This implies that

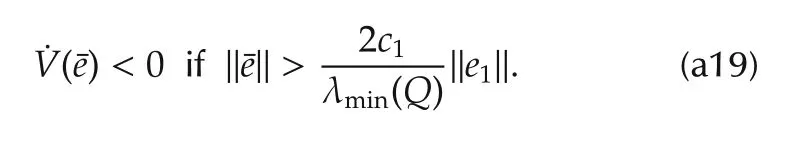
Let

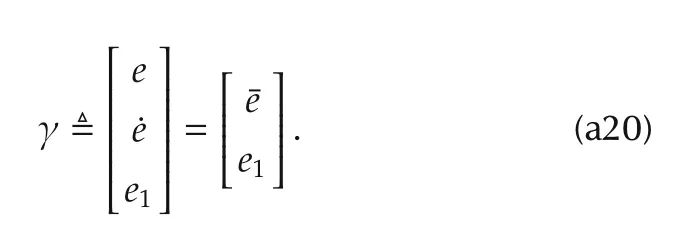
Then we have

According to the definition of the Lyapunov functionV(e),the following property holds

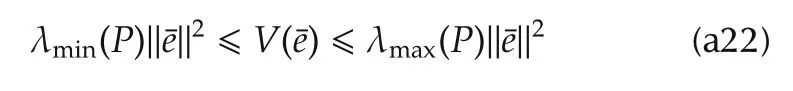
where λmax(P)denotes the maximum eigenvalue of the matrixP.

It follows from(a19)and(a22)that

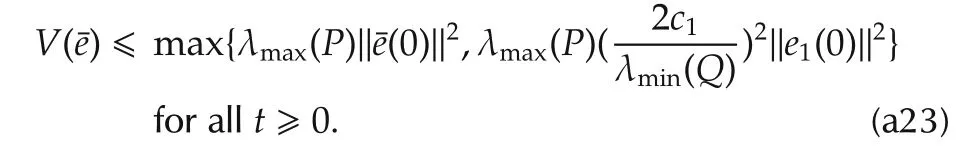
Invoking(a21)into the above inequality yields

where

Together with(a22),equation(a24)implies

wherec3is a constant depending onc2and λmin(P).

Theorem 2 shows that the estimation of the nonlinear disturbance observer(21)and(22)converges to the disturbances exponentially if the condition(26)is satisfied.This implies there exist constantsc4andd1such that

for allt≥0.

Substituting(a22),(a27)and(a26)into(a18)gives

where

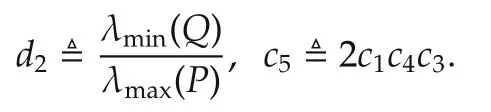
The above inequality implies that[20]

where

It follows from(a29)that

where

Invoking(a22)into equation(a31)yields

wherec7is a constant depending onc6and λmin(P).

Combining(a27)and(a33)gives

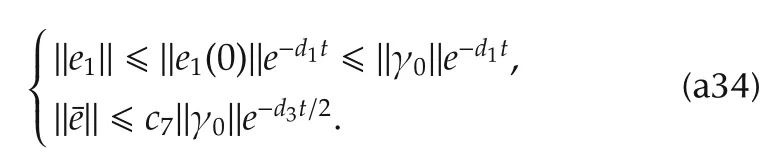
Hence the tracking errro and the estimation error closed-loop system under the nonlinear MPC(15)and the nonlinear observer(21)and(22)converge to zero exponentially.The nonlinear PID predictive controller(34)is equivalent to the composite controller when the initial disturbance estimate in the nonlinear disturbance observer is chosen as equation(31).This completes the proof. □

The physical parameters for experiments are as follows:

First and second link lengths:0.38m

Second motor mass:0.44kg

Tip mass in the end point:0.1kg

First and second link masses:0.361kg

First motor torque constant:0.23Nm/A

Second motor torque constant:0.044Nm/A

First motor voltage constant:0.29V/rad/s

Second motor voltage constant:0.047V/rad/s

Armature resistance of Motor 1:3.4Ω

Armature resistance of Motor 2:5Ω