用代数的方法解决高中立体几何问题初探
王昕阳
摘 要:用代数的方法解决几何问题,用求坐标、解方程代替辅助线、辅助面,思维单纯,容易直击目标。本文通过具体例子解说了解析法在高中幾何学习中的应用。
关键词:笛卡尔坐标系;代数方程;几何问题
学习高中立体几何,最主要的就是空间想象能力的培养,然后就是添辅助线,用几何的方法解决几何问题,这是常规的套路。自从研学了空间解析几何,笔者豁然发现用代数的方法解决几何的问题,即把图形放在坐标系里,用坐标计算代替做辅助线,解决立体几何问题会事半功倍。
一、建立坐标系,把图形放在特定的坐标系中思考
比如,异面直线之间的距离,教材中总是转化为线面距离、面面距离,也就是说需要图形中做出必需的辅助线,然后求解。例如,棱长为1的正方体ABCD-A1B1C1D1,求异面直线DB1与AC间的距离。
这本是几何问题,但若以A为坐标原点,AB为X 轴正方向,AA1为 z 轴正方向,AD为 y 轴正方向,建立笛卡尔坐标系,则D点坐标是(0,1,0),B1坐标(1,0,1),A点坐标(0,0,0),C点坐标(1,1,0),这样DB1和AC的方程可以写出,把方程改为参数方程,得x=t1,y=-t1+1,z=t1;x=t2,y=t2,z=0。这样在两条直线上任意各取一点,求得两点间距离的平方为(t2-t1)2+(t2+t1-1)2+t12,上式除以t22,可得关于t1/t2的一元二次多项式,分析什么时候取最小值,最小值是多少,这样就转化为代数问题了,利用的原理是两点间异面直线间的距离最短。
利用笛卡尔坐标系统标示法以及变数的知识,可以把几何证明问题归结为代数求解问题,在求解时可以运用全部代数方法,这样带来极大的方便。
二、练习坐标系的转化
空间建立了坐标系,空间的点就有了坐标,线或者向量就可以用它的坐标(三维数组)表示,这就是向量的代数表示。比如空间四面体对边中点的连线交于一点且互相平分,就可以用坐标计算来证明,而不是画辅助线通过几何途径来解决问题。
常见的是上面提到的笛卡尔直角坐标系,可是若空间图形直角不多,或者没有直角,那建立直角坐标系时点的坐标就不好写了,于是想到了反射坐标系。
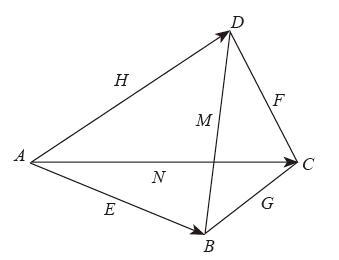
取反射坐标系,以A为坐标原点,以AB为X 轴,BC为Y 轴,AD为Z 轴,则A点坐标(0,0,0),B点坐标(1,0,0),C点坐标(0,1,0),D点坐标(0,0,1),E点坐标(1/2,0,0),F点坐标(0,1/2,1/2),G点坐标(1/2,1/2,0),H点坐标(0,0,1/2),M点坐标(1/2,0,1/2),N点坐标(0,1/2,0),则EF中点为(1/4,1/4,1/4),MN中点为(1/4,1/4,1/4)重合,所以互相平分,交于一点得证,用事实说话即可证明结论正确。
三、学会总结,提升自己的数学修养
几何问题一直是高考的难点,碰到几何问题,特别是证明,更是难上加难,如果能巧用代数计算替代证明,那会事半功倍,毕竟解方程我们做了很多年,很方便。
比如,求椭圆柱面x2/a2+y2/b2=1(a>b>0)上,过x轴并且与此椭圆柱面的交线是圆的那个平面方程。
如果设成带系数平面方程,根据已知条件求系数,那就走弯路了,换个思路,交线圆可以看成以原点为中心,以a为半径的球面与已知椭圆柱面的交线,即交线圆方程为x2+y2+z2=a2,x2/a2+y2/b2=1;这个圆在过x轴的平面上,所以它对于yoz平面的投影平面就是所求平面。确定好思路,计算上表现为从上述二式中消去 x 得y2=Z2×b2/(a2-b2),两边开根号即可得到所求的平面y=±Z×b/。
这种思路简单些,但不容易想到。就是求平面方程看成是圆的投影直线,投影在三维空间就是平面,这种知识的迁移能力是慢慢培养的。笔者坚信,高考的个性化发展会给学生的思维提供更多放飞的空间。
高中几何的半壁江山全靠辅助线当家,如果引入空间解析几何的观点,或许会为解决综合题提供更多的思路。教材与软件结合能解决更多的空间图形展示问题。
参考文献:
[1]李智.例谈转化思想在立体几何教学中的运用[J].新课程研究(基础教育),2009(6).
[2]吕林根,许子道.解析几何[M].北京:高等教育出版社,1992.

