“问题引领学习”的构建及单元教学研究

张 丹，刘 晓



“问题引领学习”的构建及单元教学研究

张 丹1，刘 晓2

（1．北京教育科学研究院 基础教育教学研究中心，北京 100191；2．海淀实验小学，北京 100048）

“问题引领学习”是指基于学生真实问题开展的学习．在这样的学习中，既将学生发现和提出问题作为学习目标，又将发现和提出，分析和解决问题作为学习的途径．基于“问题引领学习”的理念和学习模型，在“比的认识”单元中设计了真实的情境任务，鼓励学生从中发现提出问题．组织学生对这些问题进行分类，形成单元学习路线，按照此路线开展单元学习并进行问题分享会，分享学生发现和提出问题的经验．在单元实施后的后测中，实验班学生普遍反映喜欢这种学习形式，在“运用数学的眼光观察世界”方面收获最大．实验班学生问题提出的整体水平高于对照班，提出的问题类型更为丰富．

问题提出；关键能力；单元教学；比的意义

1 研究的缘起

《义务教育数学课程标准（2011年版）》（以下简称《标准》）在课程目标中规定“通过义务教育阶段的数学学习，学生能增强发现和提出问题的能力、分析和解决问题的能力”[1]，突显了“发现和提出问题”的重要性．《中国学生发展核心素养》研究成果中，提出了六大素养18个要点，其中“具有问题意识”“善于发现和提出问题”等都指出了发现和提出问题的重要性．数学问题提出能促进问题的更好解决，是发展学生创造性能力的重要途径，也是其终身学习和毕生发展的基础[2]．

纵观当今世界各国的数学教育，问题提出已成为大家关注的焦点[3]，而且教学实践都注重将儿童问题作为进一步学习和研究的基础，鼓励学生经历发现和提出，分析和解决问题的全过程．斯金纳（Skinner）要求小学生提出大量的数学问题，并对这些问题进行交流分享，形成后续问题解决活动的材料[4]．波诺托（Bonotto）以超市优惠宣传单、游乐场的宣传册作为情境，这些情境中包含着价格、百分比等数学信息．学生首先根据信息提出数学问题，并对问题进行评价．之后，教师组织学生选取问题，小组之间互相解答，最后对问题中存在的错误和解答进行讨论．通过实验，研究者发现，在这种“半结构化”的开放式任务情境中，问题提出和解决活动能够促进学生的数学创造性和审辩思维[5]．

中国的数学教育研究者和实践者，在如何为学生提供多种问题提出的活动方面也做了大量努力．但在实际教学中，学生发现和提出问题的机会却是比较少的．另一方面，虽然《标准》将发现和提出问题作为重要目标，但由于缺乏这方面的具体要求，教材和教学中即使有发现和提出问题的活动，提供的情境往往也并不开放，学生一般只能根据给出的信息提出常规问题，从而限制了学生的思考广度和深度．而教师对于学生提出的问题，往往只挑选与自己教学设计相符合的去解决，对其它问题采取了回避的态度．因此，学生的问题往往只是成为学习该课内容的“引子”，而非重要的学习素材，更不是课堂教学所要达到的目标．

因此，教师如何鼓励学生提出真问题，并真正基于他们的问题开展学习，这些都是亟待研究和实践的．研究确立了将“学生”作为数学教育研究和实践的基本立场，强调数学教学要符合学生的数学学习规律，而学生的数学学习正是不断发现问题，解决问题的过程．因此，数学教学应该重视学生的问题，运用他们的问题来引领学习．

2 “问题引领学习”的内涵与学习模型

2.1 “问题引领学习”的内涵

“问题引领学习”是指基于学生真实问题开展的学习．在这样的学习中，既将学生发现和提出问题作为学习目标，又将发现和提出，分析和解决问题作为学习的途径，从而激发学生的学习兴趣和自信心，促进学生创新意识的发展，提高学生发现和提出，分析和解决问题能力，以使学生逐步学习“用数学的眼光观察世界，用数学的思维思考世界，用数学的语言表达世界”[6]．

具体来说，“问题引领学习”包括3个要点．第一，学会提问：发展学生发现和提出问题的意愿与能力是学习的重要目标．第二，因问而学：真正的学习从学生发现和提出问题开始，不断产生问题也成为学习的持续动力．第三，问学交融：学生一方面在不断发现、提出、分析、解决问题中学习、应用和发展所学的知识和方法，一方面在学习过程中不断发现和提出新问题[6]．

2.2 “问题引领学习”的学习模型

“问题引领学习”并不是一种简单的学习模式，更是对学生学习过程的真实还原．为了避免程式化的现象，并不要求所有的学习都有固定的程序，只需要体现“问题引领学习”的基本学习模型．在基本模型下，具体的形式、时长等都可以根据需要灵活设计．图1给出了“问题引领学习”的学习模型．

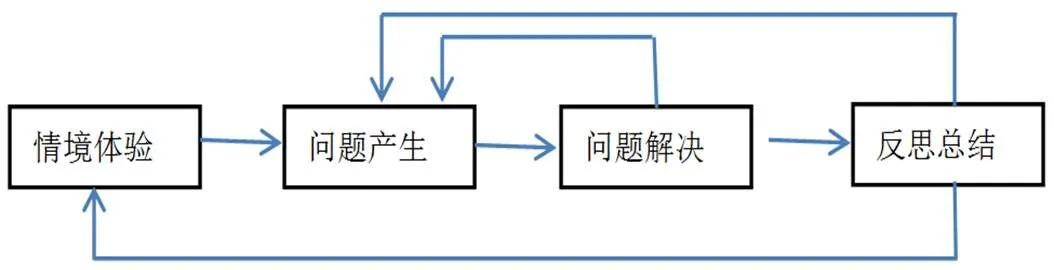
图1 “问题引领学习”的学习模型

图1呈现了一个发现和提出，分析和解决问题的全过程：学生在情境中进行体验，由于情境与已有经验产生冲突会不断产生疑问；进而经过思考，这些疑问会转化为可以讨论的问题．通过自我探索与合作交流，学生经历解决问题的过程，运用所学的知识和方法解决问题，或者进一步学习新的知识和方法．在反思中总结所学知识和方法，建立内容之间的联系．

需要特别注意的是，学生问题的产生绝不仅仅是学习的开始，正如图1箭头所示，学生不仅仅是在情境体验的基础上会产生问题，而且在尝试解决，以及反思总结的过程中，也将不断产生新的问题，这些问题又可以作为新一轮学习的开始．

总之，学生的问题作为目标、动力和途径，将一直引领着学习的发生和深入．问题引领了学生的学习需求，问题引领了学生的思维，问题引领了学生的探索和发现．

3 “比的认识”单元的整体设计

“比的认识”是六年级的学习单元，包括认识比的意义、比的化简以及利用比的意义解决简单实际问题．根据“问题引领学习”的理念整体设计了这个单元，并在北京市海淀区一所小学的六年级选择了一个班进行了实施．

3.1 设计真实情境任务促使学生产生问题

学生的问题往往来源于他们对情境中事物的好奇．研究表明，具备新颖性、复杂性、不确定性和冲突性的事物都能够引发人们的好奇心，促使人们去探索和研究[7]．“可以根据生活的经验创设教学活动，让学生在这样的活动中感悟：数学是如何利用两个数量的比合理地分析和解决问题的．”[8]

3.1.1 “比的认识”的情境任务

该单元教材一开始提供了图2的情境图，引导学生观察并思考，哪几张图片与图A像？学生初步判断图C和图E不像，图B和图D像，然后把它们放在方格纸里研究长和宽的比．

图2 教材情境

基于教材情境图，为了更加突出研究“像”与“不像”的必要性，了解面对这个现象学生还有什么其它的想法和问题？研究中创设了“拉伸照片”的情境任务，具体设计如下．

情境任务：我们在完成制作小报等实践作业时，常常需要在文档中插入长方形图片，并根据需要不断“拉伸”，以调整到合适的大小．不知你是否留意过这个过程？实际试一试，看看这里面有没有你感兴趣、值得研究的问题．

教师提前几天布置了任务，鼓励学生多实践，并将自己的思考记录在表1中，即学生进行“情境体验”．因为，“好”的问题往往是在“玩”的过程中萌发的，是人们在“玩味”所学习的事物时产生的．

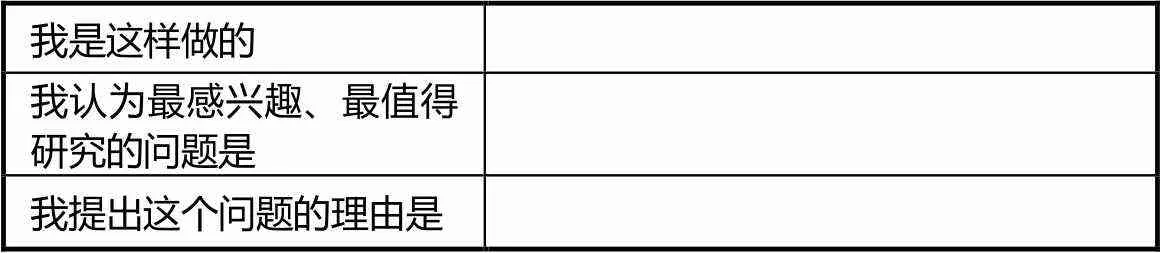
表1 “拉伸照片”中的问题记录单

学生在实际操作中观察到图片的变化，初步体验到图片是否“变形”与长方形的长、宽有关，产生学习“比”的需求．

3.1.2 学生提出的问题

根据这一情境任务，学生在充分体验之后，自然而然地发现并提出了很多有意思的问题，全班一共提出了38个问题．其中大部分问题都是关于图片拉伸前后的关系，也有一些与“比”相关的其它数学问题．具体问题举例如下．

怎样调整长和宽才能让图片不变形？

怎样放大或缩小图片，能让它与原图最为相似？

我发现虽然拉伸前后两张图片的大小不一样，但看起来很相似，这是为什么？是因为长都是宽的两倍吗？

为什么只向一个方向（左右或上下）拉伸，图片的样子会变得很怪？

长和宽同时减少一个长度，还能和原来的图片形状一样吗？

拉伸的过程中为什么出现了某数：某数？那是什么？有什么用？

听说0.618是黄金分割比，为什么它是黄金分割的？

A4纸的长与宽是如何确定的？

…………

除了数学问题，学生还提到了不少非数学问题：能否设计一个软件让图片一次性就拉伸好，为什么拉伸照片时鼠标会变成两个箭头而不是一个箭头等．一个真实情境不仅可以使问题自然聚焦到接下来需要学习的内容上，还可以突破学科的限制，引发儿童对于生活现象的多角度关注．

3.2 组织学生对问题进行分类梳理形成单元学习路线

基于学生问题开展学习，还需要将这些问题进行整理，形成单元学习路线．这一过程也是学生认真阅读问题、理解别人问题的过程．

教师提前一天布置任务，学生认真阅读每一个问题，记录印象最深的问题和不理解意思的问题．上课时，同学们首先讨论得到了该单元的学习思路，“去掉重复的问题；将这些问题找共同点，根据共同点分类；然后在同一类中选择有代表性的问题进行研究”．在此基础上，教师鼓励学生进行独立思考、全班交流，共同将这38个问题进行分类．下面是全班的分类结果．

第一类：图形拉伸前后像不像．比如：怎样调整长和宽才能让图片不变形？怎样放大或缩小图片，能让它与原图最为相似？

第二类：与“比”相关的其它数学问题．比如，什么是黄金分割比，为什么它是黄金分割的？A4纸的长与宽是如何确定的？

第三类：计算机操作．比如：能否设计一个软件让图片一次性就拉伸好？为什么拉伸照片时鼠标会变成两个箭头、而不是一个箭头等．

分类的同时，还将两个表述不清楚的问题进行了调整．分类后，学生在每一类中挑选一些有代表性的问题，比如第一类，学生挑选了“怎样调整长和宽才能让图片不变形”这一问题，解决完这一问题后再看看其它问题是否都可以解决了．对于第二类问题，同学们决定，“将其贴在问题角上，供感兴趣的同学课下研究，然后汇报研究成果．”对于第三类问题，同学们决定，“推荐给计算机老师，请计算机老师帮助解决可能的问题．”

于是，这一单元的学习路线初步确定了下来．在后续学习中学生又提出了新的问题，引领着学习的进一步深入．

3.3 鼓励学生在解决问题中开展学习并发现和提出新的问题

面对“怎样调整长和宽才能让图片不变形”的问题，教师以一位同学的问题单入手（图3），鼓励同学们尝试解决．

图3 一位同学问题单中的学习素材

通过讨论，大家感觉图片1和图片3没有变形，图片2变形了．但也有同学提出了质疑：“仅仅用肉眼判断不够，有没有其它的办法说明图片没有变形？”新的问题引发了新的探索，同学们想到了如下方法．

生1：我把图片剪下来折了折、量了量，发现图1与原图的长宽并不成倍数关系，图3的长、宽都是原图的2倍．

生2：图3与原图的关系是：宽5÷2.5=2，长8÷4=2．

生3：我们可以利用透明方格纸放在上面看一看，每副图片长是宽的几倍，看看这些倍数是否一样．

于是，大家利用方格纸测量了这些图片的长、宽，并分别比较了每幅图长是宽的几倍，以及图片1、图片2、图片3的长和宽分别是原图的几倍．最后得到如果将原图的长和宽按照一定的倍数进行拉伸，图片就不会变形．在此基础上，教师引进了“比”的概念，并引导学生用比来刻画上面情境中的关系．最后，鼓励学生描述生活情景中存在的比的关系．

“问题引领学习”的重要特征之一是问学交融：学生一方面在不断发现、提出、分析、解决问题中学习、应用和发展所学的知识、方法，一方面在学习过程中不断发现和提出新问题．在学习了比的概念后，第二节课又有学生提出了新的问题：“如果图片2、图片3都是图片1拉伸后得到的，并且都不变形，那么图片2和图片3之间长和宽的比也是一样的吧．”于是，大家一起把某一个图片在方格纸上进行拉伸，分别记录数据，得到表2．

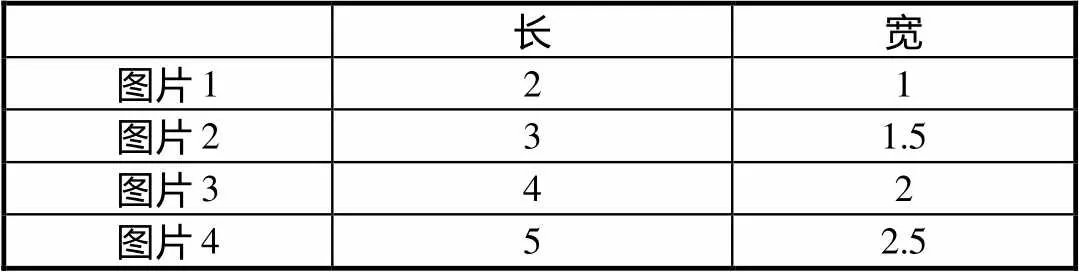
表2 图片1经过“不变形”的拉伸后得到的图形

通过分别讨论图片2、图片3、图片4长、宽的比与图片1的关系，讨论了比的化简．在此基础上，学生自然地提出疑问：“任意一个比都能够进行化简吗？商不变的规律在比中还适用吗？”由此学习了比的化简．

在这节课的最后，学生又提出了一个问题：“比及比的化简在生活中有什么用处呢？”自然引入了第三个内容“比的应用”的学习，这里限于篇幅就不赘述了．

3.4 运用问题角回应学生问题拉长思考的时间

在实施“问题引领学习”的过程中，教师面临的一个挑战是如何看待学生提出的与所学内容关系不大的问题，在“比的认识”这个单元中也不例外．此时，需要回到思考的原点：鼓励学生发现和提出问题的价值到底是什么．正如前文所阐述的，问题将引领儿童的学习需求，问题将引领儿童的思维，问题将引领儿童的探索和发现．因此，学生所有的问题都需要“回应”．斯腾伯格指出：“父母和教师针对儿童的问题，可以作出不同的反应．这些反应可以划分为7个水平，级别越高，表示中介的程度越强，儿童也就越有可能发展其高级思维技巧．”他提到的7个水平由低到高分别是：回绝问题，仅仅重复问题，承认自己无知或简单呈现信息，鼓励发问者寻找资料，提供可能的解答供儿童选择，鼓励儿童对可能的答案进行评估，鼓励儿童评估答案．最后一一验证[9]．

为了在“比的认识”单元中积极回应学生的问题，教师设计了“问题角”．“问题角”指的是：教师利用教室环境专门设置的区域，用来展示学生提出的、在班级内暂时无法解决的问题．利用“问题角”，学生将未在课堂中讨论的问题记录在上面（比如A4纸的长和宽是如何确定的），随时与其他同学分享．问题角的使用流程如图4所示．

图4 “问题角”的使用流程

这一过程不仅激发了学生提问的热情和自信，并且不知不觉地拉长了学生思考的时间．无论是学生发现问题（特别是一个有价值的问题），还是尝试去解决一个问题，都是需要过程和时间的．

3.5 举行“问题分享会”帮助学生积累发现提出问题的经验

在这个单元的最后，教师设计了一节“问题分享会”，旨在帮助学生积累发现和提出问题的经验．整节课的基本过程如下．

提前让学生回忆自己曾经发现和提出的问题，然后每人写下一个自己最满意的问题，贴在黑板上．

阅读别人的问题，为自己最喜欢的3个问题投票，统计出得票数最高的5个问题．然后请问题提出者阐述提出这个问题的背景及理由．

独立思考，小组交流，这些问题为什么会成为大家最喜欢的问题，然后修改自己的问题．

最后全班研讨，这些最喜欢的问题的共同特点是什么？什么能促使大家提出更多的“好”问题？同学们纷纷提出了自己的经验：“促使我们提问的是兴趣和好奇．”“我一直不断提问，然后自然就想到了好问题．”“生活经验让我们发现了不明白、不理解，这让我们有许多为什么，这让我们提出丰富的问题．”“我觉得很多我们没探索过的地方也有好问题，比如物理和宇宙．”“实践之后才能得出真实的想法，才能看出自己的不知，从而提出问题．其次是集体的力量，集体一起做促使我们大开脑洞．还有是同学们的问题展示，一些同学将自己想问题的不同角度展现出来，使我们有了更多角度思考问题．还有是老师的鼓励，老师一次又一次鼓励我们提出新的好问题．最后是我们的课堂汇报，每个人都想把自己最好的问题展示给大家．”

4 学生的学习效果分析

选择北京市海淀区一所小学的六年级实施了“比的认识”单元，在这所学校选择了实验班（39人）和对照班（40人）．实验班和对照班五年级下学期的期末考试成绩相当，实验班教师的教龄低于对照班．为了衡量学生问题提出的能力，课题组利用“区域教育质量健康体检项目”中的一道发现和提出问题的题目测试了两个班的学生，使用Fisher精确检验分析两个班的作答结果，Fisher精确检验=1.538，>0.05，表明两班在作答上没有显著差异．

两个班同时进行“比的认识”单元学习，实验班采取“问题引领学习”的方式，对照班没有采取此形式．两个班在该单元都使用了6课时，其中实验班3课时新授，2课时练习，1课时问题分享会（实验班6课时不包括学生提前进行的情景体验产生问题，以及问题分类形成单元学习路线）；对照班4课时新授，2课时练习．经过该单元的学习，实验班学生对此的感受如何，他们发现和提出问题的能力与对照班相比又如何呢？

4.1 实验班学生对于“问题引领学习”活动的感受

首先询问了学生是否喜欢该单元的学习方式，实验班39名学生中有36人回答喜欢，有2人回答不喜欢，1人回答80%喜欢，20%不喜欢．

进一步，借鉴文献中提到的评估学生对于问题提出活动感受的题目[10]，询问了学生“在发现和提出问题的活动中，你学习到的最重要的事情是什么？”学生们收获最大的是学会用数学的眼光观察世界，39人中有23人提到了这点．表3呈现了实验班学生认为学习到的最重要的事情．

有两位同学表示对这样的学习不喜欢，理由分别是：“因为生活中有很多活动，长时间研究一个活动我觉得没有意思．”“自己的问题被别人舍弃，心里会不好受．”还有一位同学表示80%喜欢，20%不喜欢，不喜欢的理由是：“因为老师给的问题是有范围的，我喜欢无范围的．”从理由来看，他们并不是不喜欢“问题引领学习”的方式，而是对于活动设计，以及学生问题的处理有着更高的期待，值得研究者注意．

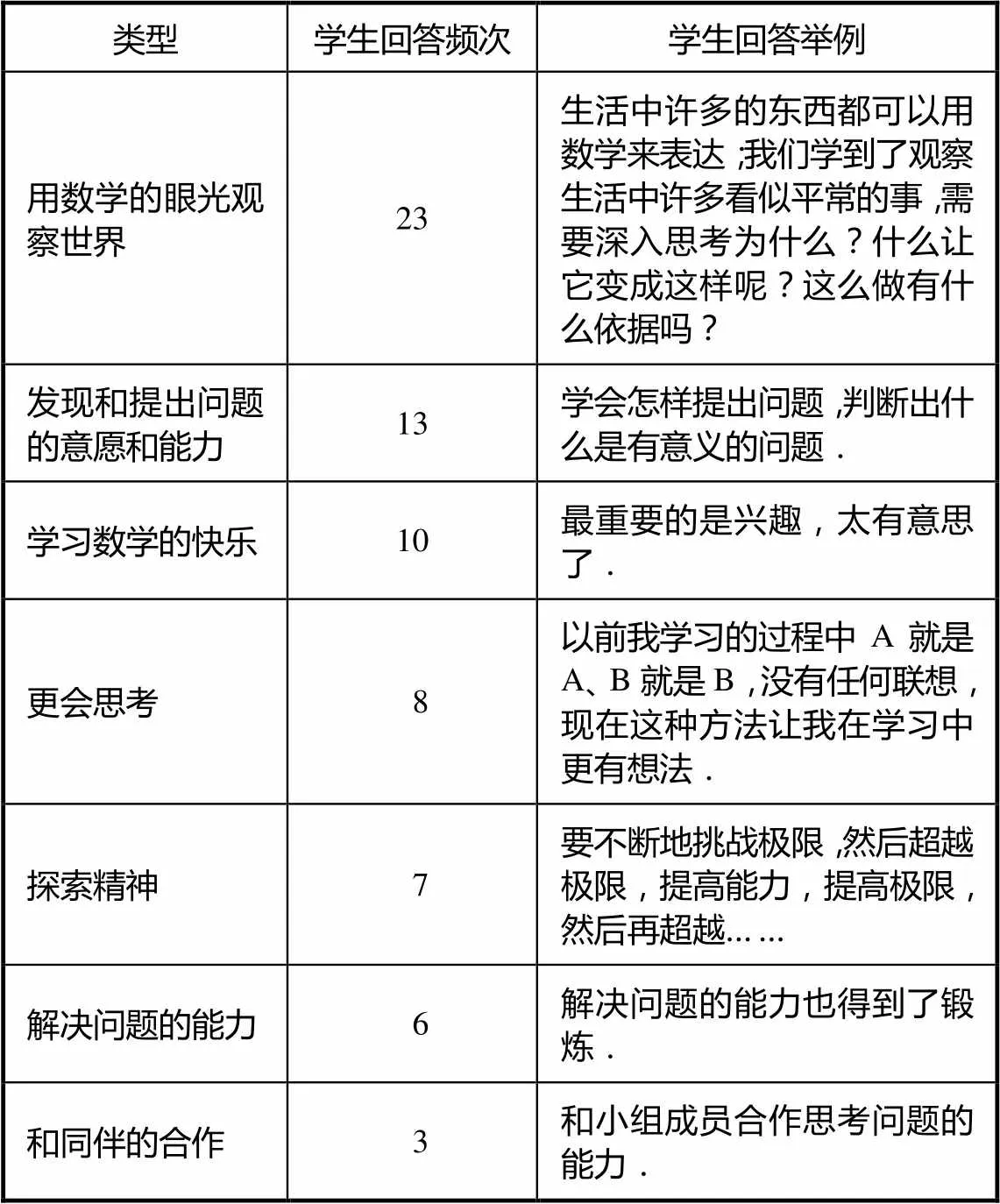
表3 实验班学生在这次活动中的收获

4.2 实验班和对照班学生问题提出的水平

为了考察学生发现和提出问题的能力，在后测中借鉴了“区域教育质量健康体验项目”的题目（见“问题单1”），要求实验班和对照班的学生共同作答．

问题单1：在停车场停车的时候肯定存在着许多数学问题．

你想到了什么？有什么想要研究的问题？

请根据要求提出3个问题：

简单的：____________________________________．

中等难度的：________________________________．

较难的：____________________________________．

（学生作答完后，下发“问题单2”）

问题单2：

（1）一辆小型车19:00驶入停车场，22:00驶出，应该交多少停车费？

（2）解决完上题后，你还能提出哪些数学问题？请尽可能多地写下你的问题．

Silver指出：问题提出涉及两个方面的活动，一是从一个情境或经验中创造出新的问题；二是对已经给的问题进行重新阐述或构想出新问题[11]．“问题单1”是鼓励学生从情境中提出问题；“问题单2”则鼓励学生根据已经解决的问题构想出新问题．后测结果是将学生在两个问题单中的所有问题综合起来加以评定的，取所有问题中水平最高的．表4呈现了问题提出水平的具体标准．

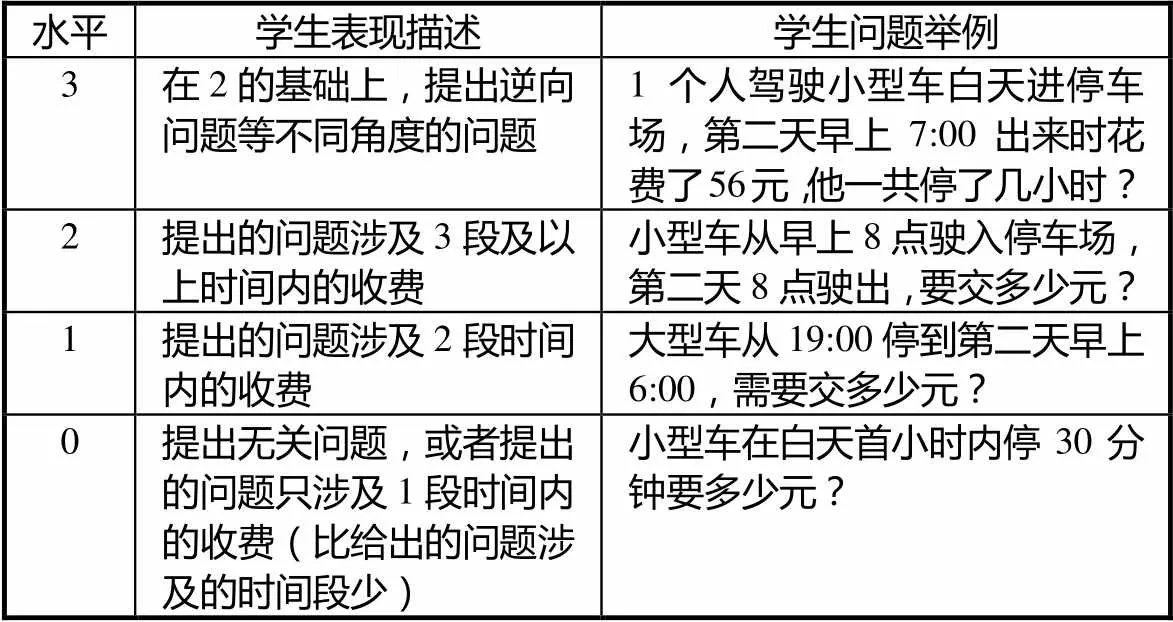
表4 学生问题提出水平划分标准

如果学生提出的问题不清楚，则按照低一个水平计算．比如，“小明家的车从早上7:00停到晚上23:00，需要花多少钱”，此问题涉及了白天首时间内，白天首时间后和夜间3段时间，应该算水平2的问题，但由于没有说清楚是小型车还是大型车，所以算水平1．

根据表4的评分标准，实验班（班级1）和对照班（班级2）的作答情况见表5．使用Fisher精确检验分析结果：Fisher精确检验=7.426，<0.05，表明两班作答上有显著差异．从各水平分布来看，实验班（班级1）约73.7%的学生在2水平以上，对照班（班级2）只有45.9%，整体而言实验班学生水平高于对照班．

表5 实验班和对照班作答水平分布

后测此题时，由于生病的原因，实验班共38名同学参加了测试，对照班共37名同学参加了测试．另外，表5去掉了合计的最后两行．

4.3 实验班和对照班学生问题提出的类型

研究中还统计了两个班学生问题提出的类型，除了与问题单2给出的求停车费的类型外，同学们还提出了如下3类问题，分别记录为类型A、类型B和类型C．

类型A：计算不是整15分钟及其倍数的时间如何收费问题．比如，小车白天在停车场如果停了20分钟，如何收费呢？

类型B：对于价钱为何如此规定的问题．比如，白天、夜间、首小时前、首小时后，大小两种型号的车的各种收费标准为什么这样规定？有什么依据？

类型C：不同时段、不同车型价钱之间关系的问题．比如，白天小型车首小时后每小时停车费为9元，夜晚为每小时0.5元，为什么差距如此之大？为什么大型车永远比小型车多交1倍的钱，它们占的面积并没有差1倍呀？

统计了两个班提出类型A、B、C问题的情况，惊奇地发现实验班学生的次数远远大于对照班，如表6．

表6 实验班和对照班提出不同类型问题的频次

综合起来，实验班学生不仅在问题提出水平上整体高于对照班，而且提出的类型也更加丰富．尤其是B、C类对于价格的“质疑”问题，正反映了实验班学生在收获中提到的“我们要有善于观察的眼睛，善于触摸的手以及一颗善于思考的心，看到生活中司空见惯的事情，一定要用心想．”“我们学到了观察生活中许多看似平常的事，需要深入思考为什么？什么让它变成这样呢？这么做有什么依据吗？”

总之，期待着用问题引领学习，进一步用问题引领学生的创新意识，用问题引领学生的好奇与自信，用问题引领学生的探究与交流，用问题引领学生的思考与实践．正如一位学生在经历“问题引领学习”后的感言：“学习就是你带着很多很多的问题，然后尝试去解决他们，接着又产生了很多很多新的问题，再去解决，如此反复的过程！”

[1] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：8．

[2] CAI J, MOYER J C, WANG N, et al．Mathematical problem posing as a measure of curricular effect on students’ learning [J]. Educational Studies in Mathematics, 2013, 83 (1): 57-69．

[3] SINGER F M, ELLERTON N, CAI J. Problem-posing research in mathematics education: new questions and direction [J]. Educational Studies in Mathematics, 2013, 83 (1): 1-7．

[4] SKINNER P. What’s your problem: posing and solving mathematical problems, K-2 [M]. Portsmouth, New Hampshire: Heinemann, 1991: 33.

[5] BONOTTO C. Artifacts as sources for problem- posing activities [J]. Educational Studies in Mathematics, 2013, 83 (1): 37-55．

[6] 张丹．“问题引领学习”：让儿童学习走向深入[J]．中小学管理，2017（6）：41-44．

[7] 约翰·巴雷尔．教会学生探究[M]．姚相全，译．北京：教育科学出版社，2016：15．

[8] 史宁中，娜仁格日乐．小学数学教科书中的比及其教学[J]．数学教育学报，2017，26（4）：1-5．

[9] 斯滕伯格，史渥林．思维教学：培养聪明的学习者[M]．赵海燕，译．北京：中国轻工业出版社，2001：73．

[10]  MEEK L K. Using problem posing as a formative assessment tool [M]. New York: Springer, 2015: 273-292．

[11]  SILVER E A. On mathematical problem posing [J]. For the Learning of Mathematics, 1994 (14): 19-28.

Research on Unit Teaching of “Problem Leading Learning”

ZHANG Dan1, LIU Xiao2

(1. Beijing Academy of Education Science, Beijing 100191, China; 2. Beijing Haidian District Experimental Primary School, Beijing 100048, China)

“Problem Leading Learning” referred to learning based on students’ real problems. In this kind of study, students were posed questions as learning goals, and would find and put forward, analyze and solve problems as a way of learning. Based on the concept of “problem leading learning” and the learning model, this study designed a real situational task in the ratio unit to encourage students to find and pose problems. Organize students to classify these problems, form a unit learning route, and carry out unit learning according to this route. Finally, a problem sharing session was conducted to share the experiences of students in finding and posing questions. In the post test after the implementation of the unit, the students in the experimental class generally liked this kind of learning form, and gain the maximum in “using the mathematics to observe the world”. The overall level of the students in the experimental class was higher than that of the control class, and the types of questions raised were more abundant.

problem-posing; key competencies; unit teaching; the meaning of ratio

2018–06–20

中国教育学会2016年度“十三五”教育科研规划重点课题——促进小学生发现和提出问题能力发展的实践研究（1601060303）

张丹（1972—），女，陕西西安人，教授，博士，主要从事数学课程和数学教学研究．

G420

A

1004–9894（2018）05–0042–06

张丹，刘晓．“问题引领学习”的构建及单元教学研究[J]．数学教育学报，2018，27（5）：42-47．

[责任编校：周学智、陈汉君]