基于云模型的基坑工程地质条件复杂性评价研究

李 明， 吴 波， 李春芳

(1. 福建工程学院土木工程学院， 福建 福州 350118； 2. 地下工程福建省高校重点实验室，福建 福州 350118； 3. 广西大学土木建筑工程学院， 广西 南宁 530004；4. 中交一公局厦门工程有限公司， 福建 厦门 361021)

0 引言

目前我国地铁工程处于大发展的时期，地铁车站基坑工程逐渐呈现出“大、深、紧、近”等特点。实践表明，当工程区域内发育有地下水、软土层、不良地质体等时，施工过程中极易出现围护结构渗透破坏、支护失稳、踢脚破坏、突涌破坏等灾害事件[1]，因此有必要对基坑工程地质条件的复杂性进行评价，从而为施工提供指导，并针对相关问题采取积极的预防措施以降低基坑工程风险。

文献[2-3]基于层次分析方法及模糊理论，构建了北京、上海、合肥、福州等地的地质条件评价模型，相关研究成果初步应用于地下空间的规划与建设中。目前在基坑工程的地质条件评价过程中存在以下问题： 1)由于测试误差和认知的局限性等原因，对地质指标进行评价时具有不确定性，表现为模糊性和随机性，传统的评价模型中往往只考虑了模糊性，而忽略了随机性； 2)定量评价指标(如土层厚度、地下水位等)往往在某一区间内变动，是一区间数而非一定值，但以往的研究中多采用定值处理，不太合理。

云模型是20 世纪 90 年代提出的一种能用于定性语言描述与定量数值间不确定性转换的模型，其以概率理论为基础建立模糊性与随机性的关联[4-6]，经过近30年的发展逐渐得到完善，在围岩分级[7-8]、岩爆预测[9]等岩土工程问题中得到了初步应用，但目前在基坑工程中的应用还较少。因此，为实现基坑工程地质条件更合理、准确的评价，有必要在相关研究的基础上对以上问题进行深入研究。本文以福建地区地铁深基坑工程为背景，考虑区域工程地质特点，构建地质条件复杂性评价的层次结构模型，采用云模型理论实现评价，评价过程中对定量指标考虑了其区间变量的特点，提出一种确定区间变量云模型的方法，最后以工程实例验证所提方法的可行性和有效性。

1 云模型理论

1.1 云模型概念及数字特征

云模型的定义[4]： 设I是一个用数值表示的定量论域，C是I上的定性概念，若定量值x∈I是定性概念C的一次随机实现，x对C的确定度μ(x)∈[0,1]是有稳定倾向的随机数，即

μ∶I→[0,1]

,

(1)

∀x∈I,x→μ(x)

。

(2)

则x在论域I上的分布称为云，记为C(x)。若x满足x∶N(Ex,En′2)，其中En′∶N(En，He2)，且x对C的确定度满足

则x在论域I上的分布称为高斯云，记为C(Ex,En,He)。

云模型一般用期望Ex、熵En、超熵He3个数字特征表示[4-6]，期望Ex是在论域空间I中最能够代表定性概念C的点，是概念C量化的最典型样本点； 熵En是定性概念C的不确定性度量，反映了在论域I中可被定性概念C所接受的数值范围； 超熵He是熵的不确定性的度量, 即熵的熵，它反映代表定性概念值的样本出现的随机性, 揭示了模糊性和随机性的关联。云模型含义如图1所示。

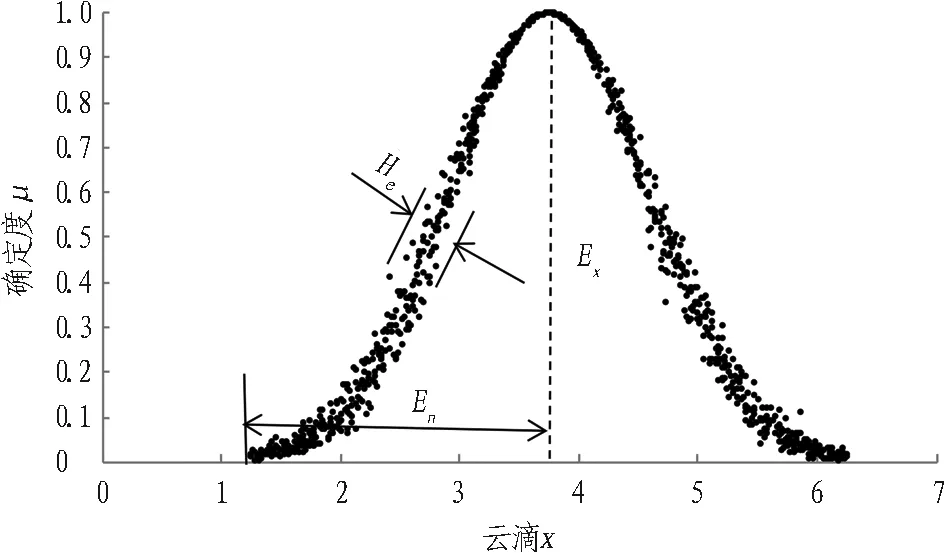
图1 云模型数字特征示意图

1.2 云模型的运算

设有n个云模型Ci(Exi,Eni,Hei)(i=1,2,…,n)，则有如下运算规则[10]成立：

其中：

式中wi为任意常数。

1.3 区间变量的云模型

设某定量评价指标的2个相邻的评价区间为A∶ [a-,a+]、B∶ [b-,b+](a+=b-)，与之对应的云模型分别为CA(ExA,EnA,HeA)、CB(ExB,EnB,HeB)，若工程实测值为区间数[d-,d+]，则参考相关区间数学理论[11]，提出以下方法确定其云模型。

1)若a-≤d-≤d+≤a+或b-≤d-≤d+≤b+(见图2)，则表示[d-,d+]完全属于区间[a-,a+]或区间[b-,b+]，则可用云模型CA(ExA,EnA,HeA)或CB(ExB,EnB,HeB)对其进行评价。

2)若a-≤d-≤a+≤d+≤b+(见图2)，则表示[d-,d+]部分属于区间[a-,a+]、部分属于区间[b-,b+]，其兼具区间[a-,a+]和区间[b-,b+]的特征，故将云模型CA、CB按实测值所占比例进行加权融合，即用如下云模型对其进行评价:

(6)

式中：λA= (a+-d-)/ (d+-d-);λB= (d+-b-)/ (d+-d-)。

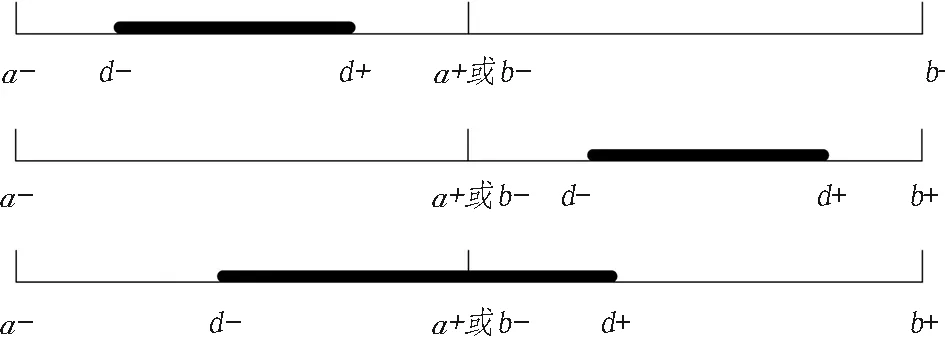
图2 指标实测值与评价区间关系

Fig. 2 Relationship between index measured values and evaluation intervals

2 基坑工程地质条件复杂性评价体系

2.1 评价因子确定

基坑施工过程中地质环境对工程活动的影响较为复杂，本文针对福建地区的地质特点、基坑工程施工过程中可能存在风险等进行分析与归纳，提炼影响工程建设的主要地质环境因子及其潜在风险[1-3,12]。

2.1.1 岩土体特征及其工程影响

1)软土层： 福建地区软土主要包括淤泥及淤泥质土，一般厚度较大，多在10 m以上。施工过程中易引发围护结构大变形，处理不当可能导致发生支撑失稳和踢脚破坏等。

2)砂土层： 砂土透水性强，当发育有地下水且围护墙的止水效果不好或止水结构失效时，地下水有可能夹带砂粒涌入基坑，使基坑产生渗透破坏，严重时造成支护结构失稳。

3)不良地质体： 东南沿海地区最常见的不良地质体是花岗岩球状风化体(孤石)，当地层中发育有孤石时，可能会造成地下连续墙等结构施工困难等问题。

4)土层组合情况： 工程范围内岩土体种类及其厚度变化情况对施工工法、施工工艺的选择有一定程度的影响，一般当土层种类较少、分布较均匀时，施工风险较低且质量较易控制，而当土层种类较多、分布不均匀时，施工风险高且质量难控制。

2.1.2 水文地质条件及其工程影响

1)局部上层滞水、潜水： 渗透破坏是基坑工程中最常见的破坏形式，当基坑工程存在局部上层滞水、潜水时，若处理不当极易造成围护结构渗透破坏，严重时可能导致发生侧壁倒塌等事故。

2)承压水： 当地层中有承压水且施工过程中未有效控制，则可能导致基坑底部发生底鼓、突涌等破坏。

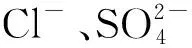
地质环境因子与基坑潜在风险之间的联系如图3所示。

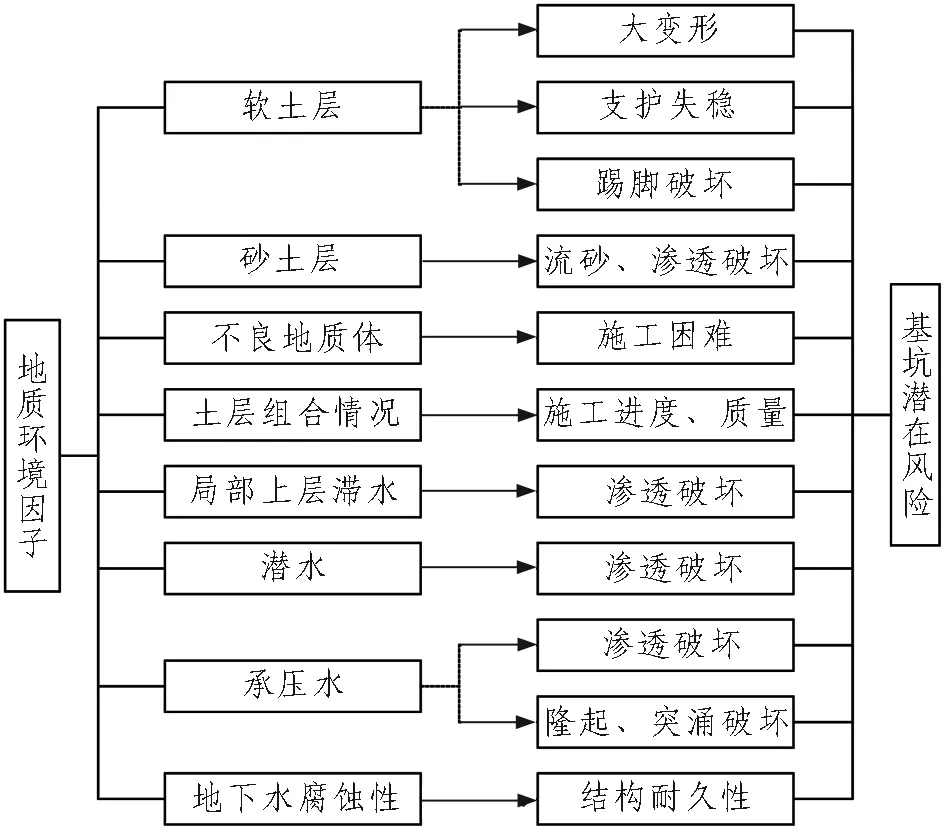
图3 地质环境因子及潜在风险

Fig. 3 Geological environment factors and potential risks of foundation pit

2.2 评价体系确定

结合以上分析，参考相关资料[1-3,12]，构建基坑工程地质条件复杂性评价体系，如图4所示。

Fig. 4 Complexity evaluation system for geological conditions of foundation pit

对地质因子进行量化时，若分级较少可能导致评价结果不准确，分级较多则计算不便。目前多划分为3～5个级别，参考相关资料[1-3,12]，本文选择目前最常用的4等级划分方法，地质因子的量化标准如表1所示。

表1 基坑工程地质因子量化标准

注： 指标U11、U12、U22的单位为m。

将定性评价语言“简单”、 “一般”、 “较复杂”、 “复杂”等映射到定量区间0～10上，分别用区间[0,2.5)、[2.5,5.0)、[5.0,7.5)、[7.5,10.0]上的云模型表示，其对应云模型的数字特征可按式(7)—(9)计算[7]。

He=k

。

(9)

式(7)—(9)中：i-和i+分别为某一等级标准的最小与最大边界；k为常数，可根据变量的模糊阈度进行调整，本文取为0.05。

对于单边界限的某变量，形如[i-,+)、(-,i+]，可先根据数据的上下限确定其缺省边界参数或期望值，然后再参照式(7)—(9)计算云参数。本文所选用的云模型的数字特征计算结果如表2和图5所示。

表2 评价等级云模型数字特征

2.3 因子权重确定

采用层次分析方法(1～9标度)确定各指标的权重[13]。对于表1中一级指标一般认为“水文地质条件(U2)”对工程的影响程度略高于“岩土体特征(U1)”的影响，参考相关文献[1-3]及专家建议，将一级指标U1、U2的权重分配为：

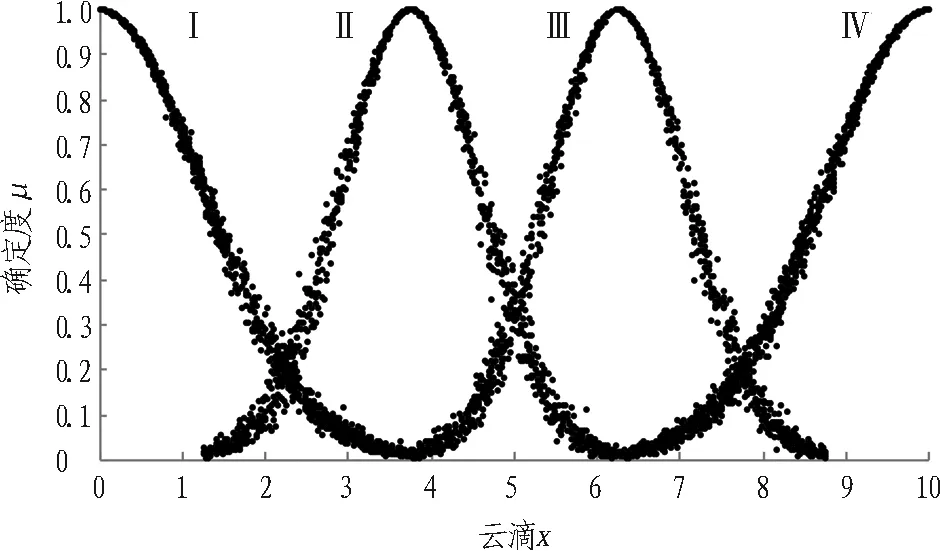
图5 评价等级云模型

。

(10)

一级指标“岩土体特征(U1)”中的各二级指标对工程影响的重要程度依次为： 软土层(U11)> 不良地质体(U14)> 砂土层(U12)> 土层组合情况(U13)，故构建以下判断矩阵：

则二级指标U11、U12、U13、U14的权重分配为：

一级指标“水文地质条件(U2)”中的各二级指标对工程影响的重要程度依次为： 承压水(U23)>潜水(U22)>局部上层滞水(U21)>地下水腐蚀性(U24)，故构建以下判断矩阵：

则二级指标U21、U22、U23、U24的权重分配为：

W2=(0.17 0.24 0.49 0.10)

。

(14)

3 工程应用

3.1 工程概况

福州地铁2号线某车站为地下2层岛式车站，车站基坑支护工程安全等级为一级，重要性系数为1.1，基坑开挖深度约16 m，车站基坑开挖地质情况自上而下为杂填土、粉质黏土、淤泥夹砂、淤泥、粗中砂、淤泥质土、淤泥、卵石等土层，车站基底座落在淤泥质土及部分淤泥层上。勘察资料显示，淤泥质土总厚度为5.3～11.3 m，粗中砂厚度为3.1～7.3 m，工程范围内无孤石等不良地质体，基坑工程地质剖面如图6所示。

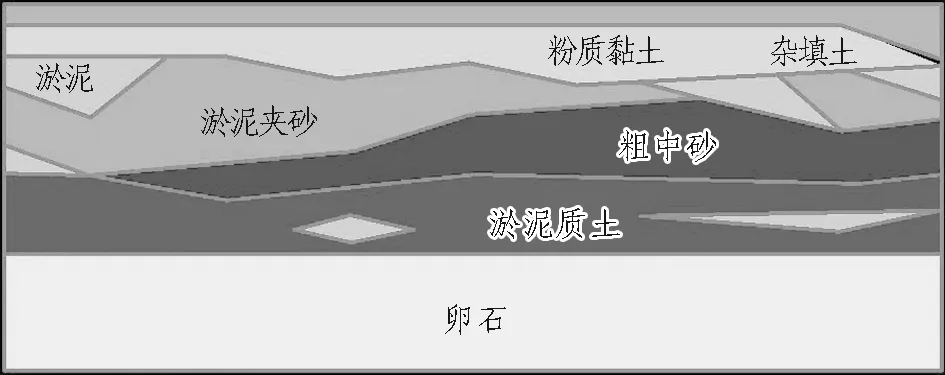
图6 工程地质剖面图

基坑开挖地层地下水较丰富，其中上层滞水发育较少； 潜水位于地表以下3～4 m，厚度为4.2～6.8 m； 承压水有2层，第1层承压水埋深1.70～3.40 m，承压水头为11.75～13.44 m，第2层承压水埋深6.5 m，承压水头为15.7～18.4 m，承压水情况较为复杂，对工程影响较为严重； 地下水水质较好，不具有腐蚀性。

3.2 基坑工程地质条件复杂性评价

结合该工程的情况，对车站基坑地质条件的各指标进行评价，其中指标“软土层(U11)”、“砂土层(U12)”、“潜水(U22)”为区间数，采用1.3节所提方法对其进行处理，地质指标评价结果及对应的云模型如表3所示。

表3地质指标评价结果及对应云模型

Table 3 Evaluation results of geological indices and their cloud models

指标状况评价等级云模型U115.3～11.3 m较复杂、复杂CU11=0.78 CⅢ+0.22 CⅣU123.1～7.3 m一般、较复杂CU12=0.69 CⅡ+0.31 CⅢU13一般一般CU13= CⅡU14分布极少简单CU14= CⅠU21一般简单CU21= CⅡU224.2～6.8 m一般、较复杂CU22=0.3 CⅡ+0.7 CⅢU23较严重较复杂CU23= CⅢU24微简单CU24= CⅠ

由式(4)、(12)、(14)，可确定基坑工程的“岩土体特征(U1)”、“水文地质条件(U2)”及“整体工程地质条件”的复杂状况对应的云模型分别为：CU1=0.49·CU11+0.17CU12+0.10CU13+0.24CU14=CU1(4.61,0.478,0.025);CU2=0.17CU21+0.24CU22+0.49CU23+0.10CU24=CU2(5.02,0.475,0.028);CU=0.4CU1+0.6CU2=CU1(4.85,0.343,0.020)。

将综合评价结果云模型CU1、CU2、CU与复杂等级评语集“简单”、 “一般”、 “较复杂”、 “复杂”的云模型CⅠ、CⅡ、CⅢ、CⅣ进行比较，结果如图7—9所示。

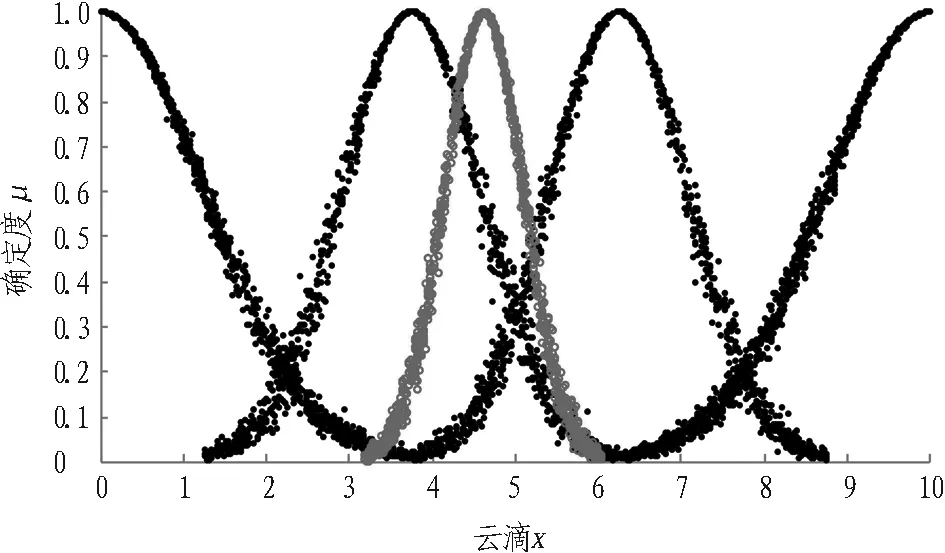
图7 岩土体特征复杂性结果

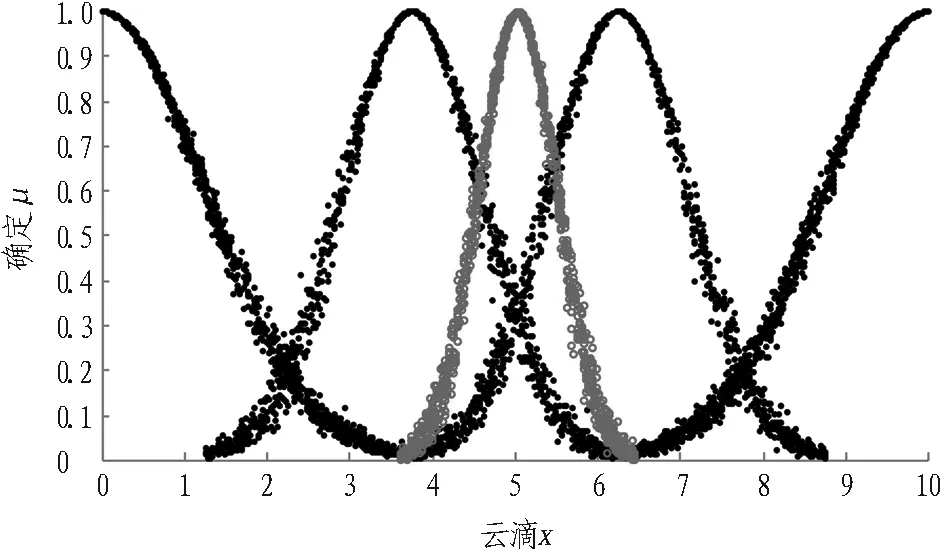
图8 水文地质条件复杂性结果

图9 整体工程地质条件复杂性结果

由图7—9可知，基坑工程“岩土体特征(U1)”的云模型的变化区间为[3.18,6.04]，介于区间[1.25,6.25]、[3.75,8.75]中，即其复杂性介于“一般”和 “较复杂”之间，其均值为4.61，与CⅡ均值的距离为0.86，与CⅢ均值的距离为1.64，即其复杂性偏向于“一般”。

“水文地质条件(U2)”的云模型的变化区间为[3.59,6.45]，介于区间[1.25,6.25]、[3.75,8.75]中，即其复杂性介于“一般”和 “较复杂”之间，其均值为5.02，与CⅡ均值的距离为1.27，与CⅢ均值的距离为1.23，即其复杂性偏向于“较复杂”。

“整体工程地质条件”的云模型的变化区间为[3.82,5.88]，介于区间[1.25,6.25]、[3.75,8.75]中，即其复杂性介于“一般”和 “较复杂”之间，其均值为4.85，与CⅡ均值的距离为1.1，与CⅢ均值的距离为1.4，即其复杂性偏向于“一般”。

因此，建议在施工过程中重点关注由软土等引起的围护结构大变形、由潜水等引起的围护结构渗透破坏和由承压水引起的基坑隆起突涌等问题。

在实际工程中，施工前对软土进行了加固处理，基坑降水方案中增设了“应急井”，同时在施工过程中加强了变形、水位监测以及巡视，通过相关措施保证了工程的顺利完成。

4 结论与建议

1)利用云模型对基坑工程地质条件评价时相关定量指标往往为区间数，考虑实测值区间[d-,d+]与相邻评价区间[a-,a+]、[b-,b+](a+=b-)的关系，基于区间数学理论提出了一种确定区间变量云模型的方法。

2)对福建地区的地质特点及基坑工程施工过程中的潜在风险进行了分析与归纳，在此基础上构建了地质条件复杂性评价指标体系； 将各评价等级划分为“简单”、“一般”、“较复杂”、“复杂”，将其映射到区间[0,2.5)、[2.5,5.0)、[5.0,7.5)、[7.5,10.0]上，并确定了对应云模型的数字特征，给出了相应评价等级对应的云模型。

3)将所提理论及方法应用于福州地铁2号线某车站基坑工程地质条件复杂性评价中，依据评价结果提出了相关工程建议，在工程实践中针对相关地质问题采取了一定的措施，保证了工程的顺利完成。

由分析结果和工程实践可知，对于软土基坑工程，地下水类型、水位高度、软土层厚度对工程安全具有主导性的影响，建议在工程评价、设计、施工过程中对其进行重点考虑。