地理国情普查数据检查中面状数据折刺检查方法的研究

徐艇伟，张彦

(1.重庆数字城市科技有限公司，重庆 400020； 2.重庆市地理信息云服务企业工程技术研究中心，重庆 400020)

1 引 言

地理国情普查通过对质量元素评分来完成数据的质量检查。其中，表征质量的折刺检查可通过电脑程序检查来完成[1]。地理国情普查的主要数据分为地表覆盖分类和地理国情要素[2]，数据类型包括点状数据、线状数据和面状数据，而面状数据是最复杂的数据类型，这意味着其折刺检查工作的难度也最大。[3]通过ArcGIS中折线夹角计算工具完成面状数据的折刺检查，存在操作过程复杂、局限性大和效率低下等问题。

随着现代计算机科学的迅猛发展，计算机在测绘、地理信息系统及遥感信息系统等地理科学行业中的作用越来越大。运用计算机语言，编写程序来完成检查是一个解决面状数据折刺检查问题的较好途径。本文通过建立面状数据的几何模型，利用计算机的迭代运算和向量夹角计算法来自动获取每个夹角的角度值，提出一套解决折刺检查问题的方案。

2 方法原理与设计

2.1 原理分析

矢量面状数据由若干个节点构成，连续3个节点形成一个夹角，当该夹角的角度小于标准阈值时，称之为折刺。寻找折刺的首要任务是实现面状数据每个夹角值的自动获取。

面状数据可以转化为点状数据，通过获取数据各个节点的位置，利用向量夹角计算法可得到每个节点所对应的夹角度数。向量夹角计算法的具体内容如下：

图1 三个节点相对位置

假设平面坐标系中的3个节点分别为P0、P1、P2，它们的排列顺序如图1所示，α表示3点连线的夹角，3个点的坐标分别为P0=(x0，y0)，P1=(x1，y1)，P2=(x2，y2)，向量夹角计算公式如下：

通过反三角函数即可获得向量夹角[4]，根据地理国情普查质量评定标准，设定最终夹角小于设定阈值的作为折刺结果导出。

2.2 技术设计

矢量面状数据折刺的检查是通过将面状数据转化为点状数据，获取点的坐标，代入向量夹角计算公式中，得到每个节点夹角的角度值，最后将角度值与设定的标准阈值进行比较，导出小于阈值的角所对应的3个节点的坐标，通过ArcGIS的点生成线工具生成最终的错误列表，技术流程图如图2所示。

图2 技术流程图

2.3 属性设计

以上技术流程的第二步需要将面状数据转换为点状数据，第六步需要生成最终的结果，具体的点状数据属性表和结果图层的属性表设计如表1和表2所示。

点状数据属性结构表 表1

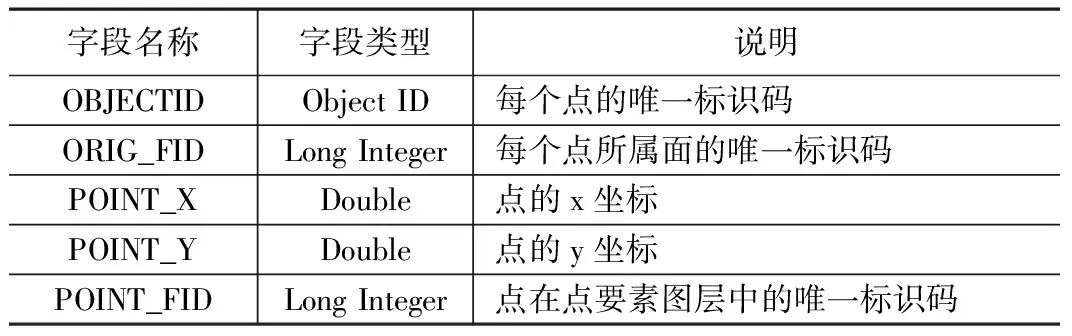
问题点图层要素属性结构表 表2

3 程序设计

3.1 面状数据转化为点状数据

该步骤是将面状数据中所有节点提取并转换为点状数据，通过调用Python的ArcPy模块中的FeatureVerticesToPoints_management函数可以完成，[5]该功能运算后效果如图3所示。

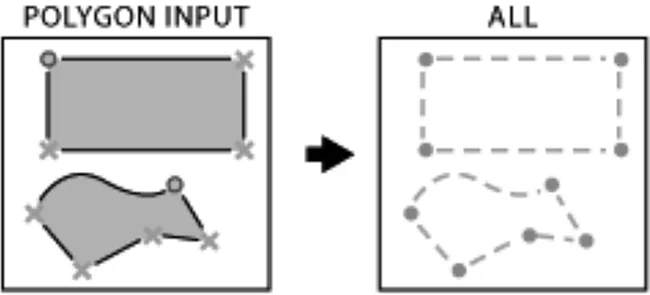
图3 面状数据转为点状数据

3.2 获取点的坐标及其前一点和后一点

(1)获取每个点的坐标

该步骤通过调用Python的ArcPy模块中AddXY_management函数，将上一步骤中点状数据的x和y值计算并记录到点位属性列表中。

(2)获取每个点的前一点和后一点

第一步，获取每个面起点和终点的信息(起点和终点重合)。由于每个面点状数据的唯一标识码从起点到终点是依次递增的，所以程序通过SQL语言获取每个面状数据中包含点状数据的最小唯一标识码和最大唯一标识码。

第二步，根据唯一标识码获取每个点的前一点和后一点的信息，每个点前一点的唯一标识码为该点唯一标识码减1，每个点后一点的唯一标识码为该点唯一标识码加1，由于起点和终点重合的缘故，所以起点和终点的前一点和后一点均是该面的倒数第二个点和整数第二个点。

3.3 计算向量夹角并比较

该步骤为本检查方法的核心步骤，具体算法流程如图4所示。

图4 算法流程图

(1)利用Python的数组List功能和Arcpy模块的Cursor功能，获取面的个数得到N值，关键代码如下：

polygons[]

with arcpy.da.SearchCursor(fc，["OID@"，"ORIG_FID"]) as cursor：#检索每个面状唯一标识码

for row in cursor：

polygons.append(row[1])

del cursor

N=len(polygons) #获取面的个数

(2)获取每个面起点和终点的唯一标识码，关键代码如下：

for m in range(1，N)：

with arcpy.da.SearchCursor(fc，["ORIG_FID"，"MIN_OBJECTID"，"MAX_OBJECTID"]，"ORIG_FID="+str(m)) as cursor： #检索每个面状数据的唯一标识码、所含点状数据的最小标识码和最大标识码

for row in cursor：

sta=row[1] #获取起点ID

end=row[2] #获取终点ID

……

(3)获取当前面起点、第2点、第3点……第n点……终点的x值、y值、前一点唯一标识码、后一点唯一标识码，关键代码如下：

with arcpy.da.SearchCursor(fc，["OID@"，"ORIG_FID"，"POINT_X"，"POINT_Y"，"Prev"，"Next"]，"OBJECTID="+str(sta)) as cursor： #获取起点的信息

for row in cursor：

x1=row[2] y1=row[3] p1=row[4] n1=row[5]

with arcpy.da.SearchCursor(fc，["OID@"，"ORIG_FID"，"POINT_X"，"POINT_Y"，"Prev"，"Next"]，"OBJECTID="+str(n1)) as cursor： #获取第2点的信息

for row in cursor：

cid=row[0] x2=row[2] y2=row[3] cp=row[4] cn=row[5]

while True：

with arcpy.da.SearchCursor(fc，["OID@"，"POINT_X"，"POINT_Y"，"Next"]，"OBJECTID="+str(cn)) as cursor：#获取第n点的信息(n≠1，2)

for row in cursor：

nid=row[0] nx=row[1] ny=row[2] cn=row[3][6]

(4)求当前面中第n个夹角值的余弦值，并通过反三角函数求得第n个夹角的角度值。构成该夹角的三个点分别为第n-1点，第n点，第n+1点，坐标值分别为Pn-1=((n-1)x，(n-1)y)，Pn=(nx，ny)，Pn+1=((n+1)x，(n+1)y)，关键代码如下：

(((n-1)x-nx)*((n+1)x-nx)+((n-1)y-ny)*((n+1)y-ny))/(((n-1)x-nx)**2+((n-1)y-ny)**2)**0.5/(((n+1)x-nx)**2+((n+1)y-ny)**2)**0.5

(5)通过条件语句对第n个夹角余弦值与标准值的余弦值进行比较，将构成超限夹角的三个点状数据导出到点问题图层中，形成初步检查结果。

3.4 生成问题线图层

为了方便检查结果显示，将点问题图层转化为线状数据，通过Python中ArcPy模块的点生成线函数可以完成。

4 试验结果与分析

4.1 试验数据

本文采用第一次地理国情普查重庆市永川区的地表覆盖分类数据来验证面状数据折刺检查方法。永川区地表覆盖分类数据为面状数据，试验区域包含面状数据共3 857个，包含节点 125 273个。

4.2 试验过程

(1)将普查数据中的地表覆盖分类数据转换为点状数据，如图5所示。

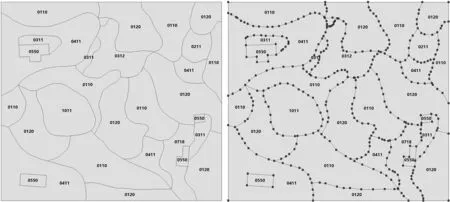
图5面状数据转化为点状数据

(2)获取点位坐标，计算3点连线的夹角，生成结果如表3所示。

向量夹角计算结果表 表3

表中记录第1824、1825、1826三个点和第7896、7897、7898三个点所构成的两个夹角值分别约为13.68°和6.07°，根据地理国情普查地表覆盖分类检查标准中面状数据折刺角度不得小于15°的规定，这六个点涉及的两个夹角均为异常折刺，作为问题点位导出。

(3)导出超限夹角，生成最终结果图层，如图6所示。

图6 问题线图层

4.3 试验分析

上述方法与ArcGIS中的折线夹角计算方法进行对比，有三大优点：

(1)适用性更广，ArcGIS的折点夹角计算只适用于线型数据，而上述方法既可以计算线型数据也可以计算面状数据；

(2)易用性更高，ArcGIS中的折点夹角计算方法需要将数据转换为点状数据后，建立COGO字段，通过COGO工具获取线段的方向角，从而得到折线夹角[7]。而利用本文论述的方法，只需要导入待检测的数据，即可运算出检查结果，不需要介入更多的人工操作。

(3)效率更高，如果使用ArcGIS的折点夹角计算方法，需要耗费的时间远比使用上述方法要长。

5 总 结

矢量面状数据折刺自动检查方法的优势是从根本上解决了基础地理数据质量检查的角度值异常问题，也为其他基础地理数据几何问题的排查提供了解决思路。该方法不仅可以运用在面状数据的折刺检查中，同样可运用在线状数据的折刺检查中。但同时也存在弊端，随着运算量增大，运算速度降低更快，当数据较大时，可通过划分查询区域、精简查询步骤以及利用已有查询结果等方法提升运算效率。计算机语言中，除了PYTHON语言，也可通过其他编程语言和平台来进行自动检查方面的开发和研究，借助计算机来完成质量检查工作将成为未来地理信息行业质检领域的一大趋势。