基于有限元和功率流理论的浮筏隔振效果评价方法研究
向祖权 居 浩 宋利飞 茅云生 傅何琪
(武汉理工大学交通学院1) 武汉 430063) (中国船舶及海洋工程设计院2) 上海 200011)
0 引 言
潜艇之类以水下作业为主的航行器在隐蔽性方面的要求都很高,敌舰通过捕捉轻微噪声引起的振动,将对潜艇的隐身性能造成毁灭性的打击,而浮筏隔振技术可以有效减少航行器内部机械的振动传递至船体,国内外在该方向都有许多研究[1-4],研究浮筏隔振情况的主要方法包括功率流法和有限元法[5-7].前者通过对每一层或子系统输入的功率流进行计算,综合考虑振动力和速度的关系,可以通过对比系统的输入和输出功率流,清楚地了解系统的减振效果,但因为理论方面的解析难度较大,只能对浮筏隔振系统进行大量简化后再对隔振效果进行计算;在计算机技术日益成熟的同时,有限元方法在复杂结构的动力学分析方面的应用也越来越广阔,并显现出其强大的优势,它可以对由多个不同部分组成的大型复杂模型进行分析计算,但是输出的评价指标较为单一,只能得出振动系统需要考察的位置的位移或者节点力[8-10],而这两者都不能全面反映结构的减振效果.
本文将有限元方法可以分析大型模型和功率流评价隔振效果更加全面正确的优点结合起来,以克服功率流方法只能对简单结构进行理论分析,和有限元方法评价效果不全面的缺点.通过商用有限元软件ANSYS构建一个将基础简化为圆柱壳的浮筏隔振系统,并对其进行模态分析及简谐激励下的谐响应分析,以此为基础,用本文提出的方法计算了输入和输出该隔振系统的功率流.
1 浮筏隔振效果评价
1.1 基于功率流的隔振效果评价
文献[11]提出了功率流的基本概念,构建了隔振系统中传递分析的功率流基本表达式.由于综合考虑力和速度及其相位关系,所以涵盖的振动信息更加完整,因此能够更加准确地对振动过程进行描述.
记Fi为在结构上某点的外部激励瞬时值,Vi为此处的速度瞬时值,那么外部激励输入此结构的功率瞬时值可以表示为
P=Fi·Vi
(1)
而实际情况下,取某一段时间内的平均功率往往可以更加准确地反映外部激励作用于结构的能量强度,即功率流
·Vdt
(2)
式中:F和V为力向量的幅值和速度响应向量的幅值;T为外部激励作用的周期。
用隔振效率来评价隔振装置的减振效果,根据功率流理论,振动的传递主要是能量的传递,采用功率流法可以合理地从能量的角度对振动进行研究.通过对隔振装置的功率流分析,可以得到设备的每一部分或每个支撑节点的能量输入情况,而功率流在通过减振系统再传递到设备支撑时,输出功率流相对输入功率流的大小是用于评估隔振系统的有效性的重要标准.
1.2 结构基本模型
浮筏隔振系统的结构见图1.l个电动机共由n个上层隔振器支撑,中间筏体和基础之间则由m个下层隔振器支撑,浮筏隔振系统的设计过程中很重要的一个环节是估算由机组输入到系统的能量Pin经过隔振系统的作用后有多少能量Pout输入到与船体相连的基础,在这个过程中,机组可当作刚性体,上、下层隔振器通常视为质量集中,并且具有复刚度的弹簧-质量-阻尼结构,中间筏体和基础在理论分析中由于过于复杂,一般被简化为弹性薄板,筏体和基础的过度简化使分析的准确程度大为降低.
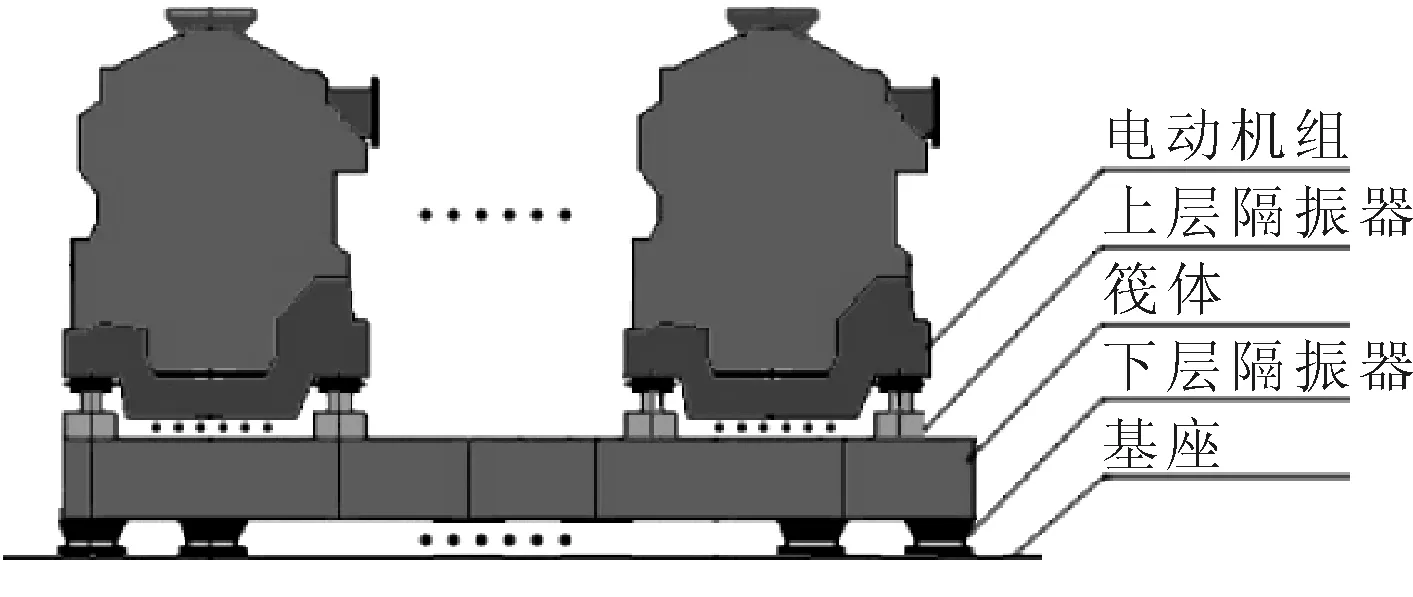
图1 浮筏隔振系统结构图
1.3 结合功率流理论和有限元方法的算法
若系统为线性,对其施加的为简谐激励,作用于结构上一点的力与速度的瞬时值分别表示为Fi和Vi,F和V为包含其相位信息的复数,则
Fi=F·eiωt
(3)
Vi=V·eiωt
(4)
将其按时间进行平均,即可得到平均功率流
·eiωt)·Re(V·eiωt)dt
(5)
式中:T为周期;ω为振动角频率.
若F*和V*是F和V的共扼转置,则式(5)可以转化为
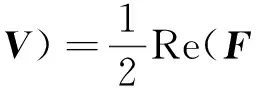
(6)
对图1中的浮筏隔振系统,输入到第i个电动机的谐响应为FAio,下标A为是机组子系统,o为作用点在该子系统质心,同样,质心速度表示为VAio,于是整个浮筏隔振系统的输入功率流为
·Re{VAo}dt
(7)
式中:FAo=[FA1o,FA2o,…,FAio,…,FAno],VAo=[VA1o,VA2o,…,VAio,…,VAno],同样,通过第j个下层隔振器的底部输入到基础子系统E的功率流可以表示为
·Re{VEt}dt
(8)
式中FEt=[FE1t,FE2t…FEjt,…FEmt];VEt=[VE1t,VE2t…VEjt,…VEmt];下标E为基础子系统E,t为作用点在该子系统上端.
假设输入为同频对称的简谐激励,任意节点i的力Fi与速度Vi具有同样的角频率,但是相位不同,因此式(3)应为
·eiωt+φF)·Re(V·eiωt+φV)dt
(9)
式中:φF为力F的相位;φV为速度V的相位.通过有限元软件ANSYS可得到位移,将式(7)中的速度矢量与位移矢量进行转换,可得到以位移量来表示的功率流:
·eiwt+φF)·lm(X·eiwt+φX)dt
(10)
式中:φX为位移向量X的相位.积分后可得
φF-φX)|
(11)
可知节点i在角频率为ωk时的功率流值
(12)
式中:Fik和Xik为振动角频率在ωk时,点i的节点力和位移;φFik和φXik为对应的相位.
结合式(5)可知,对于某一振动角频率ωk,其输入功率流等于所有电动机的输入功率流之和:
(13)
同样,结合式(6),对于振动角频率为ωk,输出的功率流则为
(14)
式中:Fik,φFik为已知的输入值;Xik,φXik,Fjk,φFjk,Xjk,φXjk则均可通过ANSYS的谐响应分析求得.
2 浮筏算例分析
2.1 模型参数选取
在本例中的浮筏系统由两个电动机,上、下层隔振器,中间筏体和薄壁圆筒形的基础组成,每个电动机由四个上层隔振器支撑,筏体由八个下层隔振器支撑,筏架尺寸为2 000 mm×720 mm×180 mm,腹板厚度为10 mm,面板厚度为8 mm.支撑基础是一个薄壁圆柱壳,直径1 200 mm、厚度10 mm、长4 000 mm,在圆柱壳内每间隔1 000 mm焊接一个厚度10 mm、宽60 mm的环形肋骨.
由于浮筏隔振系统的结构十分复杂,在建立有限元模型的时候需要采用一定的简化,机组简化为实心的立方体,用3D实体单元SOLID187来建立其有限元模型,其质量、转动惯量和惯性力矩与电机相同;筏体由薄板交错焊接,依照其尺寸采用SHELL181单元进行网格划分;隔振器可用弹性-阻尼器集中单元COMBIN14建立模型以对分析进行简化.COMBIN14单元可应用于三维以内结构中的轴向拉压和扭转,而轴向弹簧-阻尼器为单轴拉压单元,在每个节点上至多有3个自由度(沿坐标系X,Y,Z三个方向),但每个弹簧阻尼单元只能模拟隔振器一个方向的刚度,而算例中的浮筏隔振系统在三个方向都有刚度,因此同一个隔振器必须在两节点间建立三个重叠的COMBIN14单元,并分别定义其刚度方向及参数.基础支撑壳体采用与筏体相同的SHELL181单元.整个浮筏隔振系统的各层子系统采用满足各自要求的不同单元类型和划分方式,相互之间的连接通过耦合节点来实现.整个浮筏隔振系统节点数91 580,单元数78 033,所得模型见图2.左侧为主视图,右侧为隐去基座部分的浮筏系统透视图,包含下层隔振器、筏体、上层隔振器以及在其上部的两台机组.
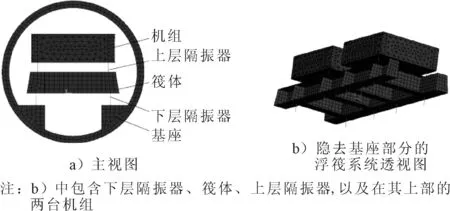
图2 复杂浮筏隔振系统有限元模型及其模型内部透视图
2.2 结构模态分析
对整个浮筏隔振系统进行模态分析,表1列出了模态分析的前30阶固有频率,图3为表1中模态频率的一些代表振型,由于整个系统是对称布置的,很明显有些很接近的模态几乎有相同的模态频率,但是模态振型则不同.
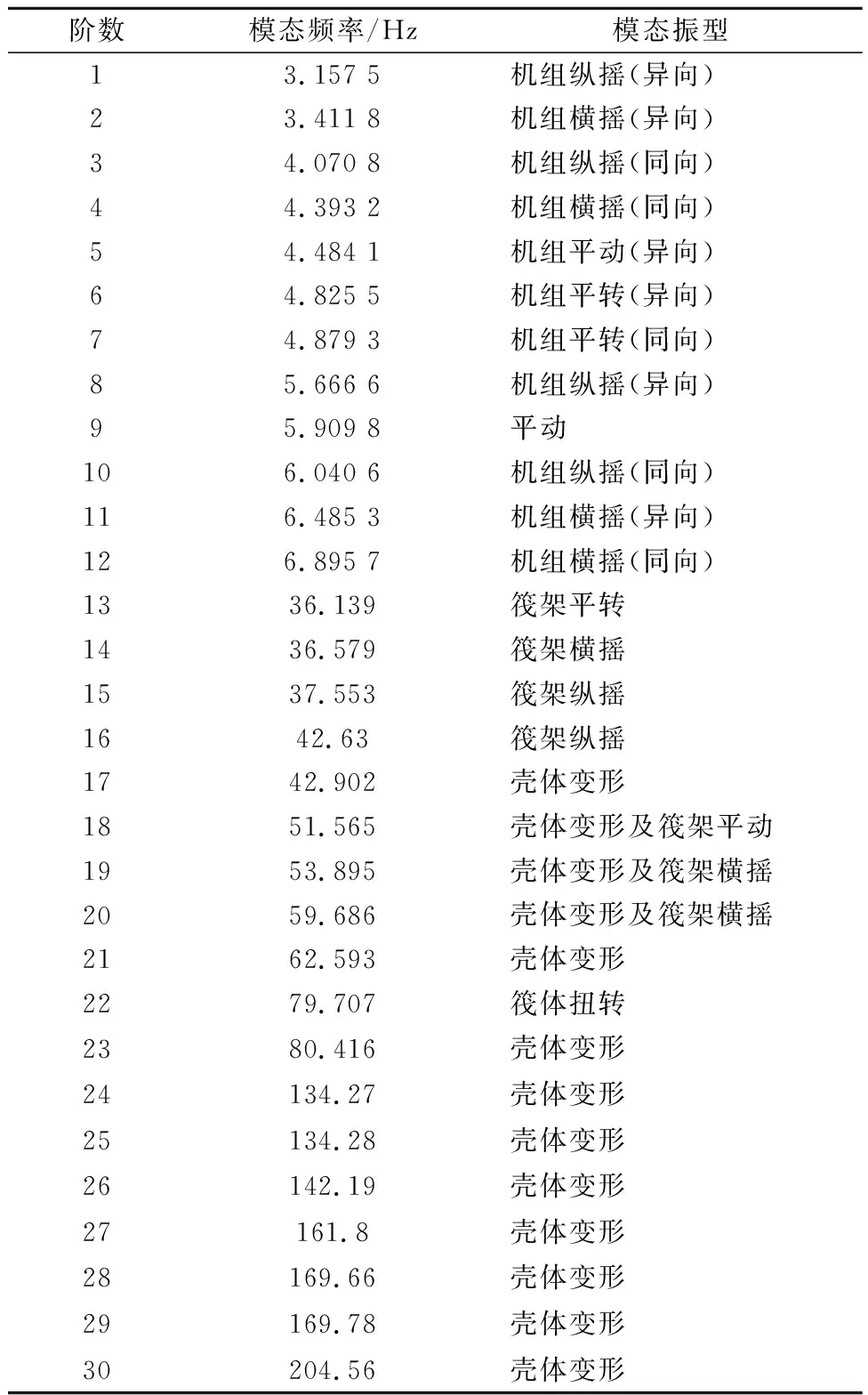
表1 系统模态参数

图3 模态振型
2.3 功率流结果分析
对两机组质心处施加垂向、横向、纵向分别为1 N的三向简谐激励组,分析的频率范围是1~300 Hz,频率取值在这一范围内主要由于舰船的低频噪声是影响其隐身性能的主要噪声区间.由谐响应分析可得A子系统中能量输入的2个节点和E子系统中能量输出的8个节点处的Xik,φXik,Fjk,φFjk,Xjk,φXjk,由式(11)~(12)可以计算每一子步所在频率处的输入输出功率流,取分析步长为1 Hz,则可得到1~300 Hz范围内所有整数频率时输入机组和圆柱壳基础的能量,即两组300个功率散点值,将二者换算为功率流与参考功率流比值之间的对数关系,以分贝为单位更容易表示,则P可定义为
(15)
式中:参考功率流Pref取10-12W.功率流计算结果见图4.
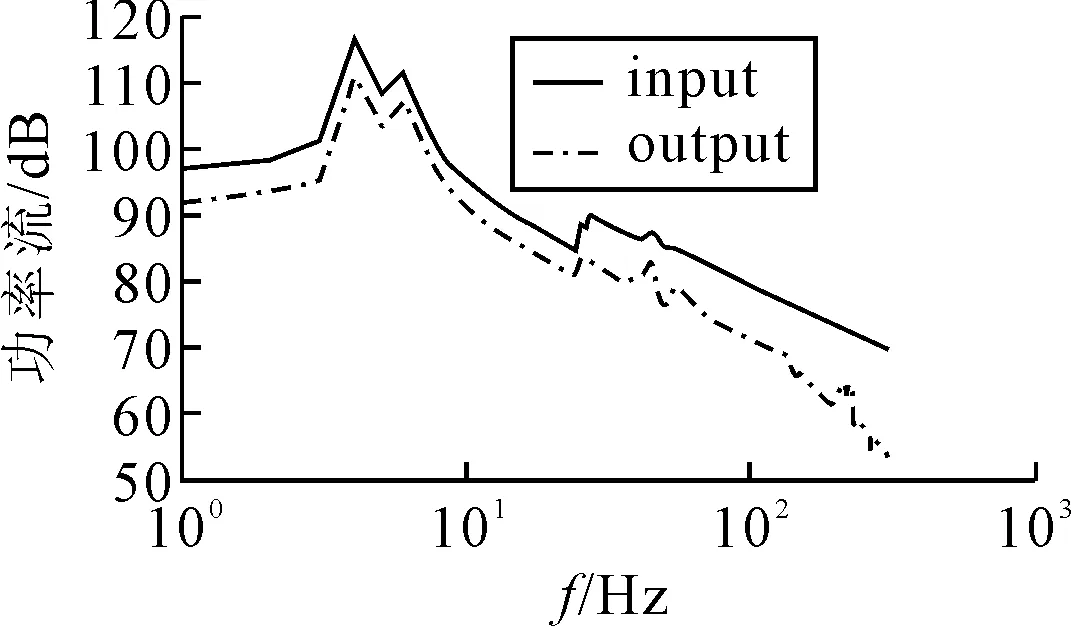
图4 浮筏隔振系统的功率流曲线
实线为由电机输入系统的功率流Pin,虚线表为输入到圆柱壳基础的功率流Pout,图4中前两个峰值对应的4,6 Hz,对应表1中这两个频率附近有许多模态聚集,同时考虑到激励是对称施加到系统上,因此,可以理解曲线峰值出现在对称谐振模态附近.150 Hz以后的隔振效果比之前优秀,且输出功率在200~250 Hz区域出现大幅波动,这是高频模态聚集的现象.通过曲线图和其他研究成果的比较[12],可以发现功率流的变化趋势特征得到了有效地体现,沿低频到中频部分的输入功率流经过浮筏隔震系统之后都得到了消除,在中频区域的隔振效果更为良好,这证实本方法的可行性.
3 结 束 语
本文在有限元方法的基础上,结合功率流理论提出了一种评价浮筏隔振效果的方法,有限元软件ANSYS能直观迅速的建立复杂结构模型,并且能方便准确的处理大型复杂结构的动力学分析,从ANSYS谐响应分析结果中提取功率流分析需要的数据进行处理,得出能更全面的评价浮筏系统隔振效果的功率流曲线.该方法给类似浮筏隔振系统这样的复杂结构的动力响应问题提供了一种解决方案.

