一种超声振动辅助粉末去除装置振子的有限元分析

仝 旭，荣佳诚，顾鸣伟，徐凯文，殷 振

(苏州科技大学 机械工程学院,江苏 苏州 215009)

0 引言

钣金车间的涂装线主要适用于对金属和非金属工件表面进行喷粉、喷漆处理，配合悬挂输送机、电轨小车、地面输送机等运送工件形成运输作业线。进行运输作业的时候，工件会通过挂钩连接在有轨小车上，挂钩的直径在1.5 cm左右，有轨小车下方的近似三角形铁板上设置有4个等间距排布的孔，孔的形状为椭圆形，短轴为2 cm，长轴为3 cm。喷粉的目的是在工件的表面喷涂粉末，但是挂钩在随工件进入喷粉室喷涂的过程中，钩子的表面会被喷涂上粉末，粘附于挂钩表面，使挂钩的直径逐渐变大，最后，当钩子的直径增大到无法放进有轨小车的挂孔和工件上直径2 cm左右的挂孔时，就需要人工用铁锤进行敲打，使挂钩两端的勾头上积累的粉末粘附物脱落，但是人工捶打不仅劳动量大，而且效率不高。

本文设计了一种超声振动辅助粉末去除装置，用于去除挂钩表面粘附的粉末。该装置主要利用连杆机构带动超声振动系统上下往复运动，超声振动系统驱动压板进行超声波振动，当压板对挂钩进行锤击和超声振动冲击时，可以快速去除粘附于挂钩两端表面的粉末，从而实现挂钩的重复利用，减少生产成本。采用有限元分析软件ANSYS对超声振动辅助粉末去除装置的振子进行结构动力学模态分析、谐响应分析和瞬态分析，可以直观、系统地揭示出该振子的输出性能，预测出振子在加载电压频率下的最佳工作效果。

1 超声振动辅助粉末去除装置的结构

超声振动辅助粉末去除装置由收粉箱、超声振动系统、套筒、连杆机构、电机、推送挂钩部分、支架部分等构成，如图1所示。超声振动系统中的振子包括超声波换能器、变幅杆和压板，如图2所示。整个振子系统通过超声波换能器的节面位置法兰与套筒连接，连杆机构与套筒连接，电机的输出轴与盘形曲柄连接。电机旋转过程中，通过连杆机构带动超声振动系统上下运动，超声波发生器为超声振动系统中的振子提供500 V的交流电压，使振子前端的压板产生超声振动。当压板对挂钩两端的勾头锤击和超声振动冲击时，即可粉碎挂钩两端的粘附物，并使其脱落。

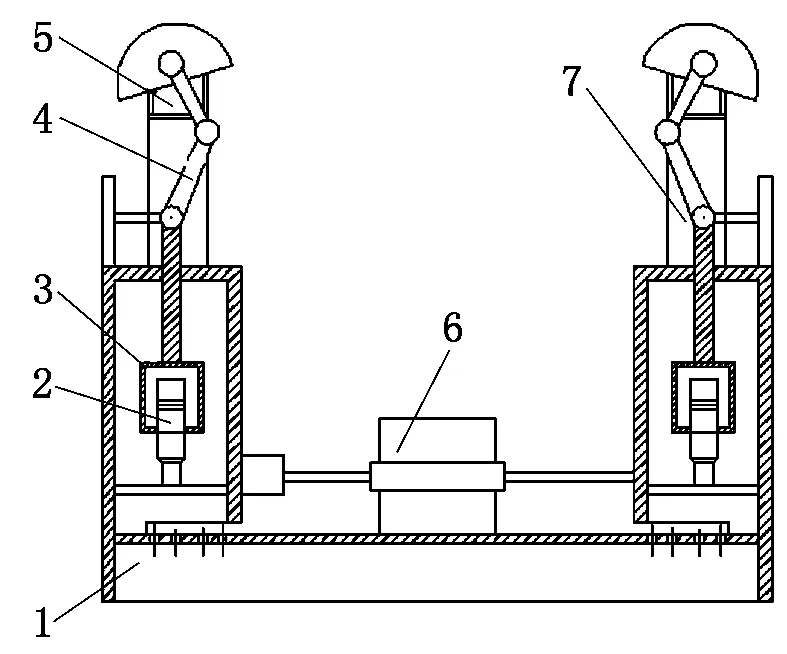
1-收粉箱；2-超声振动系统；3-套筒；4-连杆机构；5-电机；6-推送挂钩部分；7-支架部分

图2 超声振动系统简图

通过螺钉将前盖板、后盖板和压电陶瓷片预紧联接后构成超声波换能器，变幅杆通过螺钉联接设置在超声波换能器前端，压板则通过螺钉连接在变幅杆前端。超声波发生器输出的电信号作用在超声波换能器的压电陶瓷片正极和负极，由于压电陶瓷的逆压电效应，压电陶瓷片将电信号转换成超声波换能器的超声振动，振动由超声波换能器传递到变幅杆，然后通过变幅杆放大振幅后传递到压板。

根据超声振动换能器的设计原理，超声波换能器的前盖板和后盖板选用45钢，变幅杆和压板选用硬铝LY12，压电陶瓷片选用PZT-8。先以变截面杆纵振动的波动方程设计计算换能器和变幅杆的基本尺寸[1]，然后对它们整体进行有限元仿真分析，得到超声振动辅助粉末去除装置中振子的整体谐振频率， 从而实现振子的整体谐振。

2 超声振动系统振子的结构动力学分析

2.1 超声振动系统振子的模型和有限元分析

采用有限元分析软件ANSYS建立振子有限元模型，通过对该振子进行模态分析、谐响应分析和瞬态分析，获得振子的固有频率、振动模态、轴线振幅分布曲线、导纳曲线、导纳圆和幅频曲线以及瞬态振动曲线，直观地揭示出振子的输出性能，预测出该振子在加载一定频率电压下的最佳效果。

在ANSYS的前处理器中，对振子进行三维建模。振子中压电陶瓷片的单元类型选用Solid98；超声波换能器的前盖板和后盖板单元类型选用Solid95；变幅杆和压板的材料单元类型选用Solid95。采用3D自由网格对振子的三维模型进行有限元网格划分。

2.2 振子的模态分析

使用ANSYS软件，通过模态分析确定振子结构的固有频率和振型，模态分析是谐响应分析以及瞬态分析的前提条件。在ANSYS中定义材料的属性参数，然后划分网格，振子没有边界约束条件，求解后得到振子的固有频率和振型，还可以得到振动模态和轴线振幅分布。

采用模态分析模块，在压电陶瓷片的正、负极定义两个电压为0 V，采用BlockLanczos模态求解方法[2]，求解的频率范围从25 kHz到30 kHz。对振子进行模态分析后可以得到振子振动模态云图，如图3所示，振子的谐振频率为28.095 9 kHz。对该振子进行模态扩展分析，沿该振子的轴线提取路径(从压板前端到超声波换能器末端)，从而得到超声振动系统轴向和纵向的振幅分布曲线，如图4所示。由图4可知:振子的轴向振幅在压板前端最大，在超声波换能器的节面位置附近最小。

2.3 振子的谐响应分析

谐响应分析用于确定线性结构在受正弦载荷作用时的稳态响应，目的是计算出振子在响应频率范围内的受载情况，并得到响应随频率变化的振幅曲线。

振子的纵向振幅是一个微米级振动量，并且振子的振动状态会直接影响到超声振动辅助粉末去除装置的工作性能，因此要对振子进行谐响应分析，求解谐振频率下振子的响应位移。在振子负电极上加载电压0 V、在振子的正电极上加载电压500 V进行激励，采用完全法对振子进行谐响应分析，设定谐响应频率范围为26 560 Hz～29 800 Hz，阻尼比为0.03。谐响应分析后可以得到振子压板处的幅频曲线，如图5所示，在28 kHz附近，该振子的纵向振幅达到最大值，接近振子通过模态分析得到的谐振频率。通过Post26后处理器处理还可以得到振子的导纳曲线和导纳圆，如图6和图7所示。观测振子在不同频率下的导纳值，对振子与超声波电源的制作以及电路谐振匹配具有一定的参考价值[3-4]。

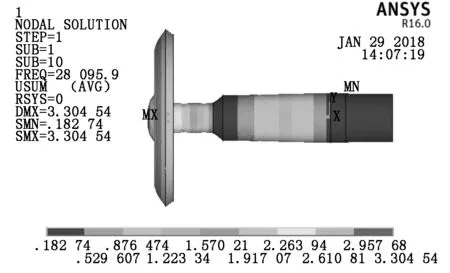
图3 振子振动模态云图

图4 超声振动系统轴向和纵向振幅分布曲线

图5 振子压板处的幅频曲线

2.4 振子的瞬态分析

对振子进行瞬态分析，确定随时间变化的振子的振幅曲线。在电极加载一个正弦激励电压，施加的电压大小为500 V，电压频率为28.095 9 kHz，并设置10个振动周期的时域。得到的振子瞬态振动曲线如图8所示。从图8可以看出:振子的最大振幅为0.875×10-7m，由于受到阻尼作用，振子并不是作振幅稳定不变的正弦运动。

图6振子的导纳曲线图7振子的导纳圆图8振子瞬态振动曲线

3 结论

设计的超声振动辅助粉末去除装置通过附加于压板的超声波振动，可以实现高效率地去除挂钩两端的粉末粘附物，从而减轻工人的劳动量，节省生产成本。使用有限元分析软件ANSYS对超声振动辅助粉末去除装置的振子进行了结构动力学模态分析、谐响应分析和瞬态分析，通过后处理工具以及数学公式运算得到了振子的固有频率和振型，以及振动模态、幅频曲线、导纳曲线、导纳圆和瞬态振动曲线，该振子的固有频率为28.095 9 kHz，在500 V的正弦电压作用下最大振幅为0.875×10-7m，这些数据以及曲线对该超声振动辅助粉末去除装置中振子的制作和优化改进具有一定的指导作用和参考价值。