基于时序变动偏差的公差分析法*

王诗雅，杨志宏，于奎刚

(山东大学 机械工程学院 高效洁净机械制造教育部重点实验室，济南 250061)

0 引言

随着科技的发展和消费者对产品要求的提高，企业亟需在产品制造、装配、使用等阶段减少成本，减低研发周期以提高自身竞争力。零件的制造偏差、装配偏差和工况偏差直接影响装配体关键尺寸的分布，从而影响产品使用性能[1]。因此，在产品开发阶段进行公差分析，研究制造、装配和工况偏差对装配体关键尺寸的影响，有助于提高产品质量，降低生产成本。

在过去的几十年中有大量的学者投身于公差分析的研究中，且已取得大量成果。徐旭松等[2]提出了一种在CAD支撑环境下的制造误差建模方法，用齐次坐标变换来描述制造偏差的传递；彭和平[3]利用小位移旋量的原理，对三维公差建模方法进行了研究；徐东等[4]在公差分析时综合考虑了零件的尺寸、形位公差以及零件配合相对位置，研究了零件偏差累积对产品性能的影响。Chase等[ 5]提出直接线性法(DLM)，以矢量来代表公差进行公差分析。Zhang等[6]提出了基于雅克比旋量法的实际工况建模方法。孙永厚等[7]提出一种基于实际工况的零件公差规范设计方法，综合考虑了零件加工工艺和实际工况对产品功能的影响；Benichou等[8]对小位移旋量法进行了改进，将热变形集成到公差分析数学模型中；冯龚等[9]考虑工况载荷下的变形，提出了一种修正公差模型；刘建永等[10]提出将变形与公差以离散点表示，建立变形与偏差累积的关系。

机械产品在实际工况下，不同时刻零件所承受的载荷不同，会产生随时间变化的变形偏差。由于零件连接间隙的存在，产品在运行过程中会产生随时间变化的配合位置偏差。这些随时间变动的偏差，本文统称为时序变动偏差。目前的公差分析方法，只考虑了静止状态下各偏差对关键尺寸的影响，忽略了关键尺寸的分布会随着时序变动偏差的变化而变化。针对这一问题，本文在前人研究的基础上提出了基于时序变动的公差分析方法，采用向量环模型原理，将时序变动偏差表示成向量的形式，并集成到装配体向量环中，实现考虑时序变动偏差的数学模型的建立。

1 时序变动偏差的影响因素

1.1 工况载荷

工况下随时间变动的交变载荷的作用会导致零件长度方向上的变形偏差，且变形偏差随着时间的变化而发生变动，进而影响产品在工况下的工作性能。因此，为了研究时序变动的变形偏差对产品性能的影响，本文将工况载荷作用下的变形偏差考虑进公差分析数学模型中。

1.2 连接间隙

机械产品通常由许多部件组成。在不同类型的连接副中，轴销与销孔之间的转动副广泛应用于装配体的组件中，且连接间隙普遍存在于转动副中。装配体在工作状态下，连接间隙的存在，使得轴销与销孔之间的配合位置发生变化，影响整个装配体的运动，产生振动和噪音，从而影响产品的性能，因此将零件之间的连接副间隙考虑进公差分析中十分重要。

本文首先采用向量环原理建立传统的公差分析数学模型，然后利用多体运动学法分析工况下零件承受的工作载荷和连接间隙引起的随时间的变化配合位置偏差，利用有限元法分析零件在工况载荷下随时间的变化的变形偏差，将时序变动偏差以向量的形式集成到传统公差分析的向量环模型中，得到考虑时序变动偏差的公差分析数学模型，最后用蒙特卡罗法对数学模型求解，得到关键尺寸的尺寸分布，如图1所示。

图1 基于时序变动的公差分析流程

2 具有时序变动偏差的机械装置

本文以四冲程发动机曲轴滑块装配体为例，如图2所示。该装配体由曲轴、连杆、活塞销和活塞组成。本文主要分析某型发动机活塞销主轴线到曲轴主轴线之间的尺寸，它对发动机的一些设计指标如压缩比、冲击、振动和噪声均具有重要影响，因此，把该尺寸看作曲轴滑块装配体的关键尺寸。

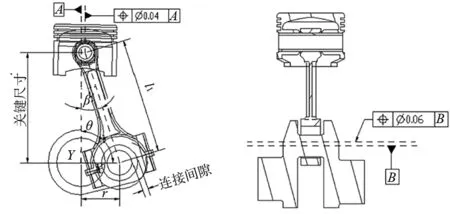
图2 具有时序变动偏差的曲轴滑块机构

实际工作过程中，曲轴滑块机构处于稳定工作状态时，曲轴的转速为3000r/min。每个工作循环，曲轴绕主轴线转两圈，总曲轴角度为720°。详细的尺寸公差和几何公差如表1所示，r为曲轴旋转半径，l为连杆长度，a为活塞位置度偏差，b为曲轴与连杆的配合位置偏差。θ为曲轴与坐标轴Y之间的夹角，β为连杆与Y轴之间的夹角。

表1 曲柄连杆装配体的公差特征数据

3 基于时序变动偏差的公差分析

本文采用蒙特卡罗法对发动机曲轴滑块机构一个工作循环(曲轴转动两圈)内，曲轴变形、曲轴与连杆的配合位置偏差和初始规范公差对关键尺寸的影响进行了研究，θ为0时为曲轴滑块机构的初始状态。

3.1 公差分析数学模型

由图3知，关键尺寸KD与曲轴旋转半径、曲轴变形量、曲轴连杆之间的配合位置偏差、连杆长度、活塞销位置度偏差等参数相关，这些参数是最终装配偏差的来源，也是影响发动机性能，如压缩比、振动和噪声等的重要因素。

传统公差分析方法中，影响关键尺寸各参数组成的向量环模型如图3a所示。此时关键尺寸与各相关偏差的函数关系为：

(1)

但在实际应用时需要考虑曲轴的变形以及曲轴与连杆的配合位置偏差，修改后的向量环模型如图3b。此时函数关系的数学模型如式(2)所示，my(t)表示曲轴的变形偏差，ny(t)连接间隙引起的曲轴与连杆之间的配合位置偏差。

my(t)+ny(t)

(2)

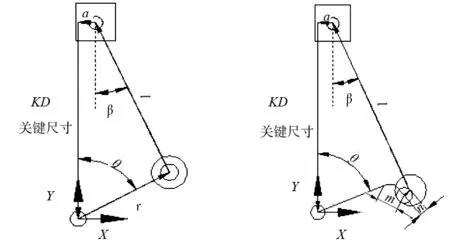
(a)传统向量环模型 (b)考虑时序变动偏差向量环模型图3 曲轴滑块装配体向量环模型

由以上可知，要得到关键尺寸的分布，需得到各相关参数的值。尺寸和几何公差为已知条件(见表1)，接下来需要研究曲轴的变形偏差my(t)以及曲轴与连杆之间的配合位置偏差ny(t)。

3.2 时序变动偏差

3.2.1 曲轴的变形偏差

当发动机高速运转时，曲轴承受活塞连杆组传递的交变载荷作用，受力情况(见图4)极其复杂，很容易发生变形，由于装配约束的原因，其变形偏差将参与装配偏差的传递与累积，为充分研究曲轴变形对装配体关键尺寸的影响，本文采用有限元和多体系统仿真分析软件结合的方法，建立曲轴滑块多体动力学模型，获得曲轴工作时的动态载荷，继而利用有限元法对曲轴进行变形分析。曲轴变形量的大小与材料有关，曲轴的材料为35Mn2Mo28，其密度为7.84g/cm3，弹性模量为70000N/mm2，泊松比为0.3，线膨胀系数为11.1×10-6mm/℃。

图4 曲轴滑块机构曲轴受力分析图

由图4知，活塞连杆组通过连杆将载荷作用于曲轴，与连杆的旋转惯性力组合成总载荷Fl。本文采用多体动力学原理，模拟仿真装配体在实际工作下的运动过程，仿真分析得到曲轴在工况下承受载荷Fl如图5所示。

图5 曲轴在一个运动周期内承受载荷变化

得到曲轴在工况下承受的载荷后，将曲轴导入ANSYS软件划分网格，设置约束、边界条件和曲轴在工况下承受载荷，求解得出曲轴在半径方向上的变形量如图6所示。从图中可以看出，曲轴在轴径方向的最小变形量为0mm，最大变形量为0.0577mm。一个周期内，最大变形分别发生在0，0.02和0.04时刻。

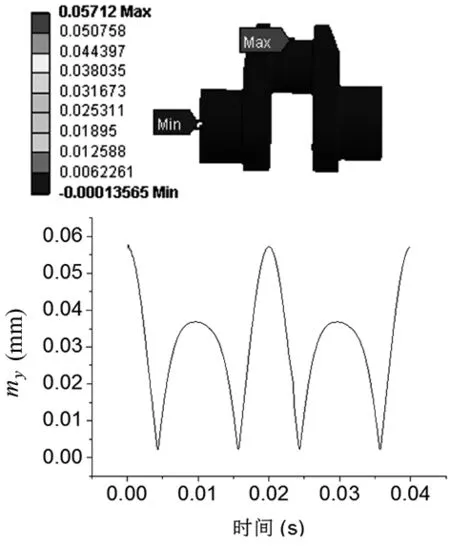
图6 曲轴在半径方向上的变形量

3.2.2 连接间隙引起的配合位置偏差

在曲轴滑块装配体中，旋转副存在于连杆轴销与曲轴轴瓦的连接配合中，由于连接间隙的存在，在旋转运动过程中会导致零件配合位置的变化，如图7所示。

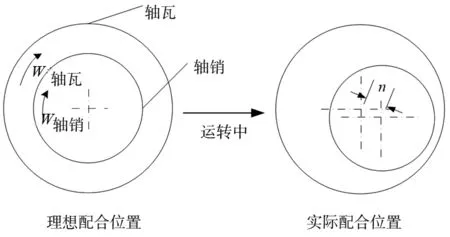
图7 在旋转运动中零件之间的配合位置偏差

为了获得配合位置偏差ny(t)，本文利用动力学原理，将曲轴滑块三维装配体模型导入ADAMS中，设置曲轴与连杆之间的连接间隙为0.03mm。仿真分析一个运动周期得到配合位置偏差如图8所示，从图中可以看出，配合位置偏差的最大值为0.03mm，最小值为-0.03mm，最大配合位置偏差大约发生在0.015和0.035时刻，最小配合位置偏差大约发生在0.005和0.025时刻。

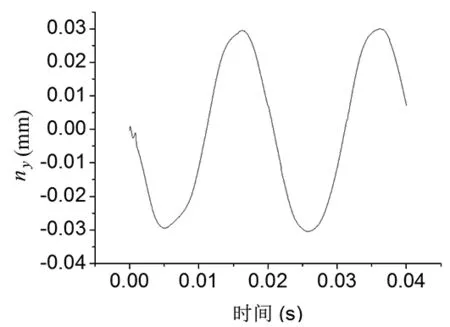
图8 曲轴与连杆之间的配合位置偏差

3.3 结果与讨论

为了得到关键尺寸的分布，接下来利用蒙特卡罗法求解方程(1)和方程(2)。在计算过程中参数r和l被看作服从正态分布N(45,0.02/3)和N(138,0.1/6)的随机变量，参数a被看作服从正态分布N(0,0.02/3)的正态分布，my和ny被看作处于[0,0.0577]与[-0.03,0.03]之间的随机变量。设置蒙特卡罗仿真次数为50000次，得到传统公差模型和基于时序变动公差模型下，关键尺寸的分布如图9所示。

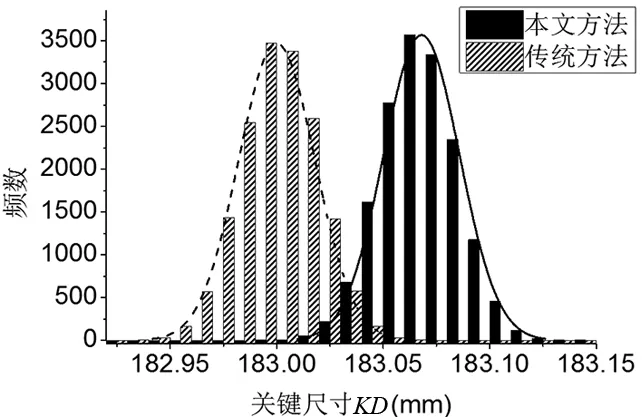
图9 某一时刻两种公差分析法关键尺寸的分布

表2 某一时刻关键尺寸相关数据对比

由表2知，关键尺寸的公差大小基本不变，尺寸分布的均值发生变化，传统方法的关键尺寸的均值为183mm，而本文方法的关键尺寸的均值为183.0682mm，意味着关键尺寸的分布向右平移了约0.07mm。为了计算不同时刻，本文方法相对传统方法，关键尺寸分布相对平移量，本文利用蒙特卡罗法分别计算了不同时刻关键尺寸分布的均值，得到不同时刻点本文方法相对传统方法，关键尺寸正态分布的偏移量如图10所示。

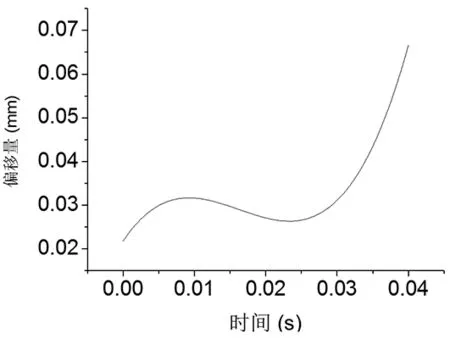
图10 不同时刻本文方法相对传统方法关键尺寸分布偏移量

从图10关键尺寸分布偏移量与时间关系曲线图看出，不同时刻，关键尺寸的分布的偏移量不同。在t在0s时，本文提出的公差分析法求解出的关键尺寸的分布相对传统公差分析法，向X轴正方向平移了0.0224mm，而在t为0.04s时，关键尺寸的分布向X轴正方向平移了0.0682mm。由缺陷率的计算公式1-num(USL-LSL)/num(sample)知，关键尺寸分布的偏移会导致产品的缺陷率的变化。而不同时刻，关键尺寸分布的偏移量不同，缺陷率固然不同，静态下的公差分析不能准确预测产品实际工作性能。因此，本文提出的基于时序变动的公差分析方法更能精确预测产品的性能。

4 总结

本文考虑了实际工况下的时序变动偏差，如随时间变化的变形偏差和由于连接间隙导致的随时间变动的配合位置偏差，提出了基于时序变动偏差的公差分析法。借助向量环模型原理，将时序变动偏差用向量形式表达，并集成到装配体向量环中，建立考虑时序变动的公差分析数学模型。采用蒙特卡罗法对数学模型进行分析计算，得到不同时刻关键尺寸的分布。本文提出的方法对比传统的公差分析方法，得出时序变动偏差会导致关键尺寸的分布发生偏移，导致不同时刻产品的缺陷率不同，从而验证了基于时序变动公差分析法更能精确的预测产品的性能。