基于耦合机器学习模型的洪水预报研究

阚光远，洪 阳，梁 珂

(1. 清华大学 水利系，北京 100084；2. 中国水利水电科学研究院 北京中水科工程总公司，北京 100048； 3. 中国水利水电科学研究院 水利部防洪抗旱减灾工程技术研究中心，北京 100038)

机器学习基于仿生学发展而来，通过模拟人脑的功能解决实际问题。机器学习方法通常由一系列数值算式和数学变换组成，通过现代电子计算机及软件程序实现其功能。众多机器学习方法中，人工神经网络(ANN)的关注度最高。近年来，随着反向传播训练算法的提出以及现代图形处理器(GPU)引发的高性能计算革命的兴起，ANN技术迎来了第二春。以深度学习、强化学习等技术为代表的现代ANN已成功应用于多个领域，主要包括：计算机视觉、自然语言处理、文本识别、自动驾驶汽车、人工智能甚至围棋对弈等领域[1-3]。

许多学者尝试将ANN技术应用于洪水预报领域[4-7]，取得了许多有益的成果。然而，由于洪水预报工作的高度复杂性，ANN的训练和测试精度仍不能同时达到满意的效果。因此，提升ANN的预报能力和稳定性需要进一步研究。ANN性能尚不能令人满意的主要原因如下：①传统ANN模型通常基于当前和前推若干时段的降雨和实测径流量预测当前时刻的径流量，这种建模方式导致模型的预见期只有一个计算时段长，给径流滚动连续预报带来了困难；②传统ANN通常使用试算法来确定网络拓扑结构(即隐含层神经元个数)，网络拓扑结构确定后，再进行参数的训练。这种两步式训练方法不能同时优化网络拓扑结构和参数，训练得到的网络往往不是最优结果。隐含层神经元个数取得很大时虽然可以得到很好的训练精度，但进行预报时，网络的泛化能力往往很差，预报精度衰减严重。减少隐含层神经元个数虽然对提升网络的泛化能力有益，但可能导致训练精度下降。因此，传统的两步式训练方法费时费力，面临上述难题；③由于试算拓扑结构和基于梯度下降的反向传播训练算法是局部优化方法，传统两步式训练方法得到的网络拓扑结构和参数往往不是全局最优的，局部极小问题严重；④实际应用中，单一的ANN往往不能取得满意的效果，需要与其他机器学习方法相配合来提升精度。

为了解决ANN应用中面临的以上4个问题，本文提出了一种耦合机器学习模型，并用于流域洪水预报。该模型通过独特的建模方式将ANN与K最近邻方法相耦合，利用多目标遗传算法和Levenberg-Marquardt算法进行全局最优训练。在屯溪流域小时尺度洪水预报中的应用表明，耦合机器学习模型的精度和可靠性较好，具有较好的应用前景。

1 研究区域与数据

本研究基于屯溪流域。屯溪流域的自然地理特征介绍如下：屯溪流域位于我国东南沿海的安徽省皖南山区，流域集水面积2 690 km2，是新安江水库的重要入库站。屯溪流域植被覆盖良好，主要包括常绿针叶林、落叶阔叶林、混交林、林地、草地和牧草地等。土壤类型主要为黏壤土。流域位于亚热带季风气候区，年平均温度17 ℃，冬季干冷晴朗，盛行西北风；夏季高温、湿度大、日照强烈，盛行东南风。春秋两季台风频发，冷热交替频繁，春夏两季多发锋面雨，夏秋两季多发台风。季风风向与山岭走向相垂直，山岭阻挡台风和北方冷空气的推进。屯溪流域高程自西向东递减，最大、最小和平均高程分别为1 398、116和380 m。

屯溪流域的降雨与产流特征介绍如下：流域年平均降水1 600 mm，降水年内年际变化剧烈。50%洪水发生在4-6月间，20%洪水发生在7-9月间。径流年内年际变化剧烈。1996年6月30日，新安江流域发生新中国成立以来最大洪水，暴雨如注，河水骤涨，洪峰抵达中心城区适逢深夜，尽管水文部门做出了洪水预报，但警报不及时，洪魔肆虐，中心城区一片汪洋，屯溪老街商铺淹没水深2 m有余，沿河两岸一片狼藉，损失惨重。在灾后反思中，黄山市政府下决定建设“黄山市洪水预报预警系统”，系统于1997年5月建成，成为当时安徽唯一的集信息采集、数据处理、洪水预报为一体的综合应用系统，在1998年、1999年、2001年和2006年洪水预报中发挥巨大作用。由此可见，洪水预报模型在防洪减灾中的作用是十分关键的。

屯溪流域雨量站、河网和DEM见图1。屯溪流域小时尺度降雨径流预报基于29场场次洪水，其中20场用于模型率定，其余9场用于模型检验。场次洪水时间范围从1982-2002年。流域具有11个雨量站，用于计算流域面平均雨量。

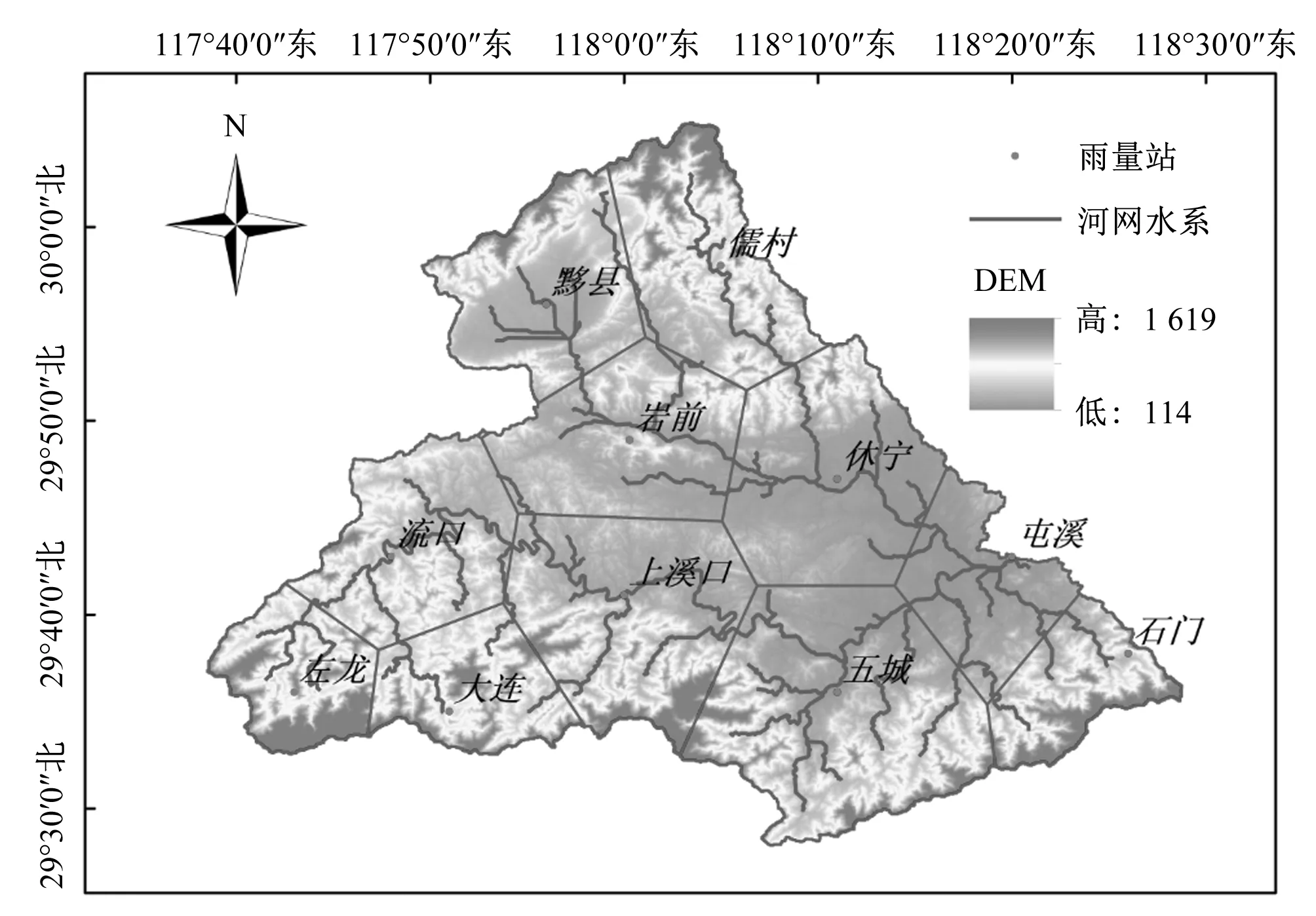
图1 屯溪流域图Fig.1 Map of the Tunxi watershed

2 耦合机器学习模型

2.1 降雨和前期径流阶数识别

流域出口径流的模拟与预报基于多个预报因子，包括：降雨和前期径流。降雨是产流的主要驱动因子，包括当前时刻降雨和前推若干时刻的降雨组成的序列。流域干湿状态(主要由土壤湿度反应)是产流的另一个关键影响因子，由于数据驱动模型无法计算土壤湿度，因此采用前期径流来表征流域的干湿程度。前期径流由前推若干时刻的径流序列组成。以上预报因子作为模型输入，驱动模型进行径流预报，具体建模方式见2.2小节。

降雨和前期径流需要前推的时段数称为模型的阶数。阶数对于模型预报精度和稳定性十分重要，阶数过小，模型能够获取的信息量有限，导致预报精度下降；阶数过大，会引入冗余信息，导致率定期精度高而检验期精度低的“过拟合”问题。本研究采用基于偏互信息的特征选择算法辨识模型阶数，许多研究表明，该方法适用于非线性模型输入变量选择，具有精度高、冗余信息少的优点，是一种非常优秀、成熟的输入变量和阶数识别算法[8-10]，该算法的具体细节详见相关参考文献。阶数识别的具体步骤为：

(1)确定降雨和前期径流阶数的上限。基于对流域历史降雨-径流资料特性的分析，估计出降雨形心至洪峰之间的滞后时段数，阶数上限取稍大于该滞后时段数的数值。

(2)根据2.2小节中的建模方式，将当前时刻降雨、前推若干时刻降雨及前推若干时刻径流作为候选输入变量，前推时段数的最大值设置为阶数的上限。

(3)将候选输入变量作为输入，对应时刻的径流量作为输出，采用基于偏互信息的输入变量筛选方法进行迭代计算，求出候选输入变量，即确定了阶数。

2.2 人工神经网络-K最近邻方法耦合径流预报

耦合机器学习模型基于降雨序列和前期径流序列实现流域出口径流过程的预报，其建模方式如下：

(2)

Q(t)=Qest(t)+Eest(t)

(3)

式中：Qest和Eest分别为径流量和径流量误差的估计值；FANN和FKNN分别为基于ANN和K最近邻(KNN)算法的径流量和径流量误差估计方法；P和Qant分别为降雨和前期径流；nP和nQ分别为降雨和前期径流的阶数；Q为预报的径流量。

径流预报的流程为：首先，估计Qest；然后计算Eest；最后，将Qest和Eest相加求得预报径流量。第一时段计算时，前期径流采用实测值，随着计算时段的步步推进，将新求得的Qest值作为后续计算的前期径流带入以上公式，就实现了不需要实测前期径流，而利用模型输出的预报径流量作为前期径流的连续预报功能。由于这种建模方式利用了前期径流的信息，且不需要前期径流的实测值(而是用模型预报值代替)，通过耦合ANN和KNN两种算法，相互取长补短，实现了高精度连续预报[11-15]功能，有效延长了预见期，克服了传统ANN模型只能提前一个计算时段进行径流预报的不足。

2.3 基于多目标遗传算法和Levenberg-Marquardt算法的ANN拓扑结构和参数优化

为了实现网络拓扑结构和参数同时全局优化的目的，利用一种能够将网络拓扑结构和参数同时编码为一个实数序列的编码方式[5]，将实数序列作为多目标非制约排序遗传算法(NSGA-II)的决策变量进行全局优化，获取网络拓扑结构和初始参数。然后通过Levenberg-Marquardt反向传播算法对网络进行进一步精细训练，获取最终的参数。多目标遗传算法的目标函数采用预报精度和网络复杂度两个目标，可在训练精度和网络复杂度间取得良好折中，在保证训练精度的前提下，有效提高了网络的泛化和预报能力。在获取的帕累托(Pareto)解集中选择具有最佳预报精度的网络结构作为最优网络结构。ANN训练完毕后，通过留一交叉验证方法对KNN算法参数(最近邻个数)进行优选。

3 研究结果

3.1 散点图分析

实测和预报径流散点图见图2。由图2可知，率定和验证精度均令人满意。率定期和验证期的回归系数R2分别可达0.963 5和0.951 5。率定期散点图中点据分布均匀。检验期散点图中点据分布较率定期稍差，点据分布较为离散，其R2值比率定期稍差。尽管检验期结果比率定期稍差，耦合机器学习模型在检验期的精度也是令人满意的。率定期至检验期精度衰减比率为0.951 5/0.963 5≈0.987 5，衰减程度较小，可以满足洪水预报精度需求。由图2(b)可以发现，检验期预报径流与实测径流相比，有所低估。

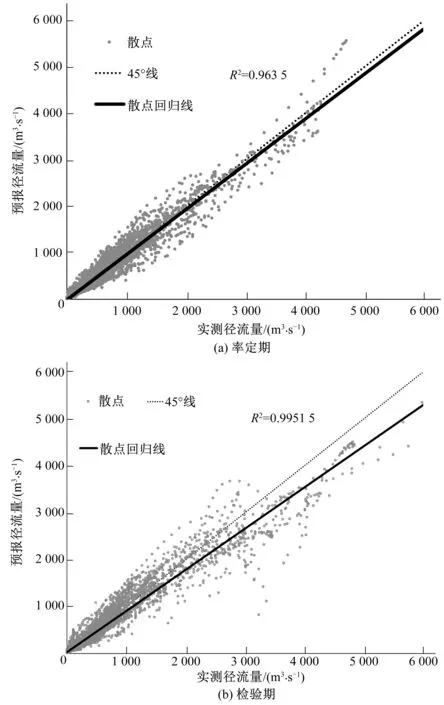
图2 实测和预报径流散点图Fig.2 Scatter plots of observed and forecasted discharges

3.2 径流过程线分析

图3中展示的是率定期和检验期典型洪水场次模拟与实测过程线。通过观察所有场次洪水预报过程线可知，耦合机器学习模型的预报精度较好，过程线比较光滑，取得了满意的预报效果。良好预报效果得益于新型建模方式和新型模型更强的预报能力。经过阶数优选的降雨输入序列为模型提供了充足的水量信息，可以取得更好的水量平衡结果。光滑的过程线和良好的预报精度得益于前期径流序列的贡献。前期径流序列确保了模型计算的连续性，提高了模型预报的稳定性。

3.3 场次洪水误差分析

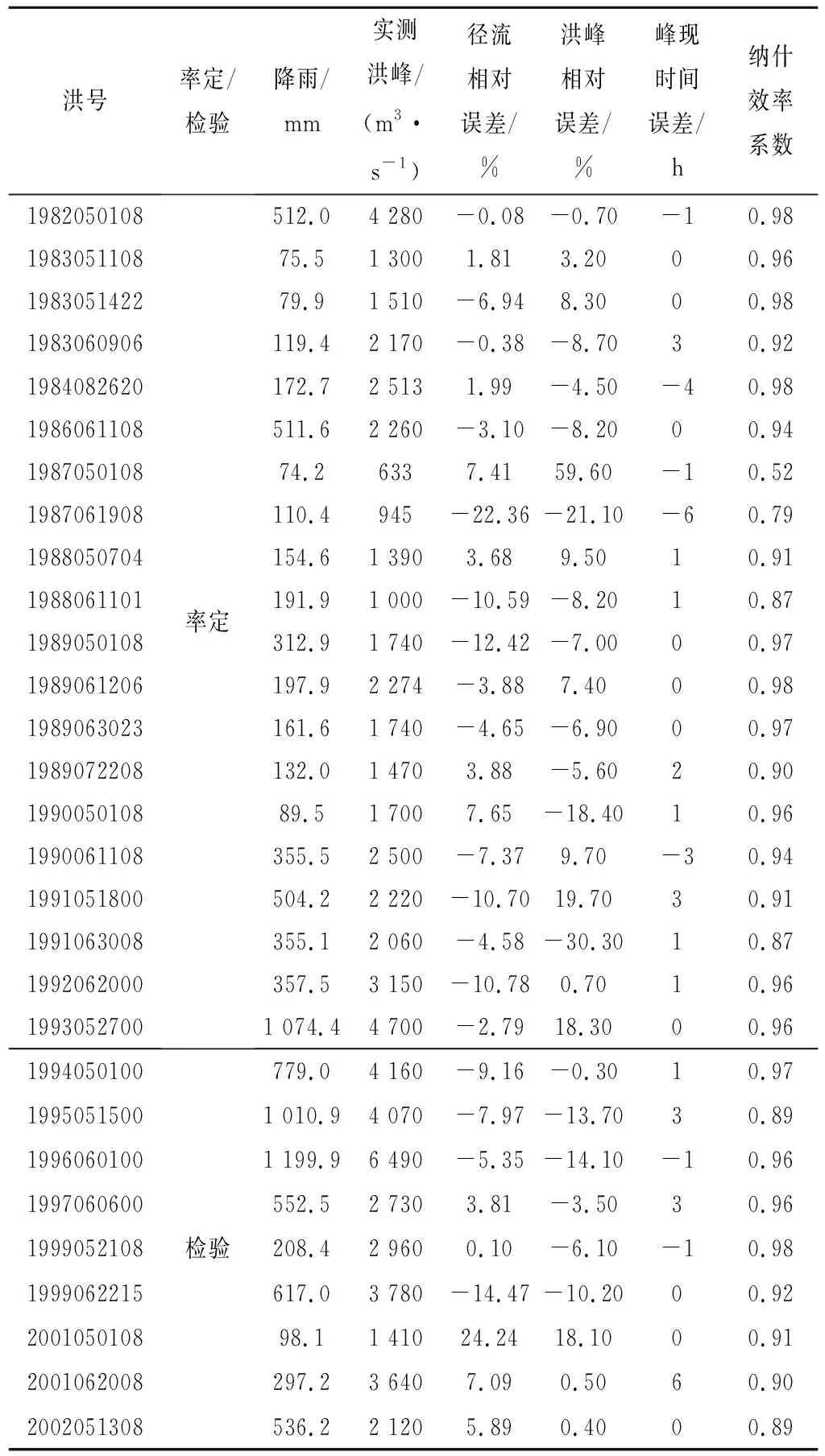
场次洪水误差统计结果见表1。由表中结果可知，率定期和检验期精度均令人满意。实测洪峰范围为633～6 490 m3/s。

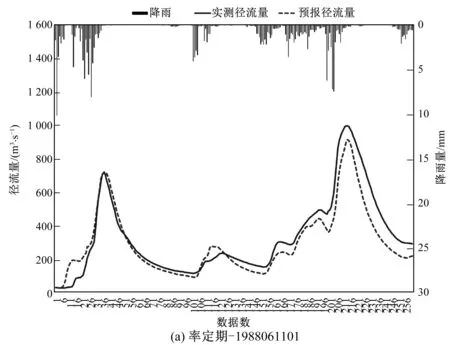
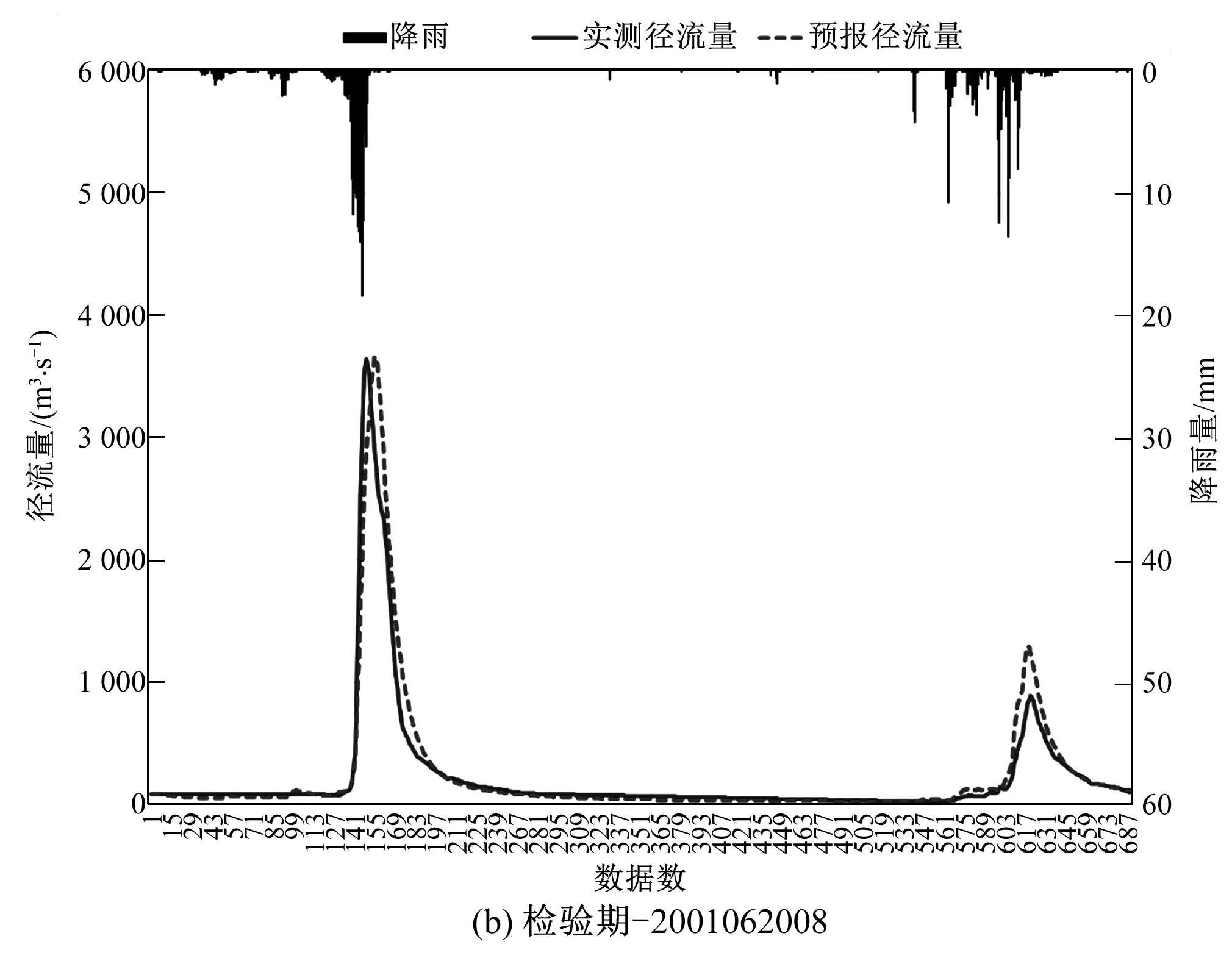
图3 率定期和检验期径流过程线图Fig.3 Hydrographs of calibration and validation periods

洪号率定/检验降雨/mm实测洪峰/(m3·s-1)径流相对误差/%洪峰相对误差/%峰现时间误差/h纳什效率系数19820501081983051108198305142219830609061984082620198606110819870501081987061908198805070419880611011989050108198906120619890630231989072208199005010819900611081991051800199106300819920620001993052700率定512.04 280-0.08-0.70-10.9875.51 3001.813.2000.9679.91 510-6.948.3000.98119.42 170-0.38-8.7030.92172.72 5131.99-4.50-40.98511.62 260-3.10-8.2000.9474.26337.4159.60-10.52110.4945-22.36-21.10-60.79154.61 3903.689.5010.91191.91 000-10.59-8.2010.87312.91 740-12.42-7.0000.97197.92 274-3.887.4000.98161.61 740-4.65-6.9000.97132.01 4703.88-5.6020.9089.51 7007.65-18.4010.96355.52 500-7.379.70-30.94504.22 220-10.7019.7030.91355.12 060-4.58-30.3010.87357.53 150-10.780.7010.961 074.44 700-2.7918.3000.961994050100779.04 160-9.16-0.3010.9719950515001 010.94 070-7.97-13.7030.8919960601001 199.96 490-5.35-14.10-10.961997060600552.52 7303.81-3.5030.961999052108检验208.42 9600.10-6.10-10.981999062215617.03 780-14.47-10.2000.92200105010898.11 41024.2418.1000.912001062008297.23 6407.090.5060.902002051308536.22 1205.890.4000.89

实测总降雨范围为74.2～1 199.9 mm。率定期最大和最小洪峰为4 700 m3/s和633 m3/s。检验期最大和最小洪峰为6 490 m3/s和1 410 m3/s。检验期洪峰流量值范围超越了率定期数据集，便于对模型泛化能力进行进一步的检验。以下从径流深相对误差、洪峰相对误差、峰现时间误差和纳须效率系数4个方面开展误差分析。

3.3.1 径流深相对误差

率定期中，出现14个负误差值和6个正误差值，表明模型率定结果倾向于低估径流深。检验期中，出现4个负误差值和5个正误差值，表明检验期并未显著高估或低估径流深。率定期中，仅有一场洪水(1987061908)的径流深相对误差的绝对值超过20%。检验期中，仅有一场洪水(2001050108)的径流深相对误差的绝对值超过20%。以上结果表明，耦合机器学习模型的径流深预报精度较好，检验期精度更优，具有很好的泛化能力。

3.3.2 洪峰相对误差

率定期洪峰相对误差范围为-30.3%～59.6%。有三场洪水的洪峰相对误差绝对值超过20%，分别为1987050108、1987061908和1991063008。检验期所有洪水的洪峰相对误差绝对值均低于20%。率定期中，有11个负误差值和9个正误差值。检验期中，有6个负误差值和3个正误差值。以上结果表明，率定期结果并未明显高估或低估洪峰流量，但检验期对洪峰流量有所低估。场次洪水1996060166的洪峰流量为率定期和检验期的最大洪峰，耦合机器学习模型的预报精度很好，洪峰相对误差小于20%。尽管该场洪水超过了率定期数据集的范围，模型在率定期并未学习过如此大的洪峰流量，在检验期仍取得了很好的预报结果，说明耦合机器学习模型具有很好的泛化能力。

3.3.3 峰现时间误差

率定期和检验期分别有两场和一场洪水的峰现时间误差超过了3 h。总体来讲，耦合机器学习模型的峰现时间误差预报结果较好。率定期中有5个负误差值和8个正误差值。检验期中有2个负误差值和4个正误差值。耦合机器学习模型预报的洪峰比实测洪峰总体上略有提前。

3.3.4 纳什效率系数

从纳什效率系数结果来看，耦合机器学习模型精度很好。大部分场次洪水的纳什效率系数可达0.9以上。只有1987050108和1987061908两场洪水的纳什效率系数较低，分别为0.52和0.79。这两场洪水属于小量级洪水，洪峰流量分别为633 m3/s和945 m3/s。由于洪水量级较小，因此洪水非线性较强[16]，导致模拟结果略差。

3.4 资料代表性与可靠性分析

对所有29场洪水资料进行了代表性与可靠性分析，具体介绍如下：

(1)率定期洪水。率定期洪水总降雨量与洪峰流量关系图见图4。由图4可知，场次洪水总降雨量的范围是74.2～1 074.4 mm，洪峰流量的范围是633～4 700 m3/s。最小总降雨量对应的场次洪水恰好具有最小洪峰流量，最大总降雨量对应的场次洪水恰好具有最大洪峰流量。随着洪峰流量由小变大，虽然存在几场洪水的总降雨量有所波动，但总降雨量的变化趋势总体上是增加的。这表明率定期洪水降雨-径流资料的量级变化趋势是合理、一致、可靠的。

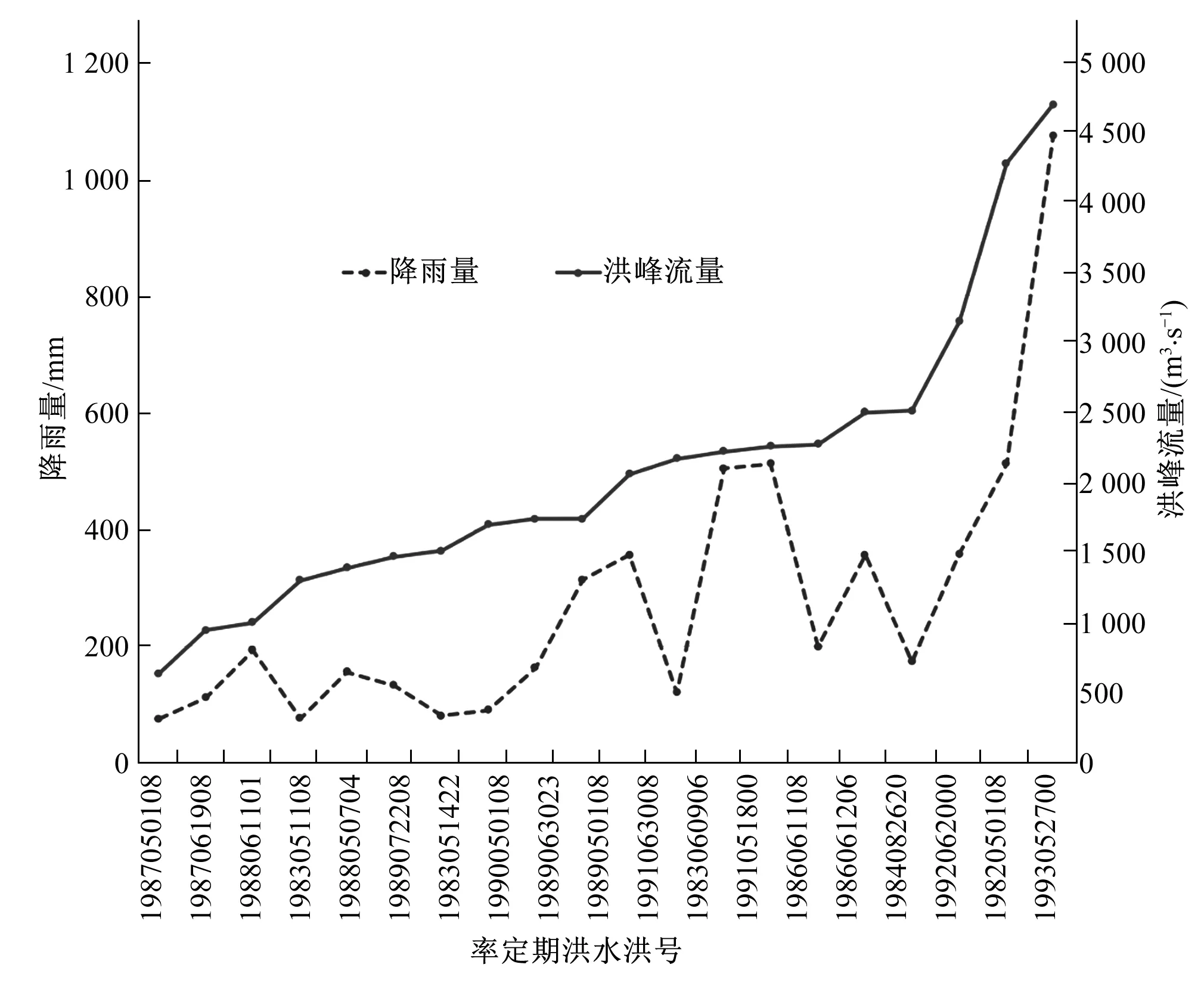
图4 率定期洪水分析Fig.4 Flood analysis of calibration period

(2)检验期洪水。检验期洪水总降雨量与洪峰流量关系图见图5。由图5可知，场次洪水总降雨量的范围是98.1～1 199.9 mm，洪峰流量的范围是1 410～6 490 m3/s。最小总降雨量对应的场次洪水恰好具有最小洪峰流量，最大总降雨量对应的场次洪水恰好具有最大洪峰流量。随着洪峰流量由小变大，虽然存在几场洪水的总降雨量有所波动，但总降雨量的变化趋势总体上是增加的。这表明检验期洪水降雨-径流资料的量级变化趋势是合理、一致、可靠的。

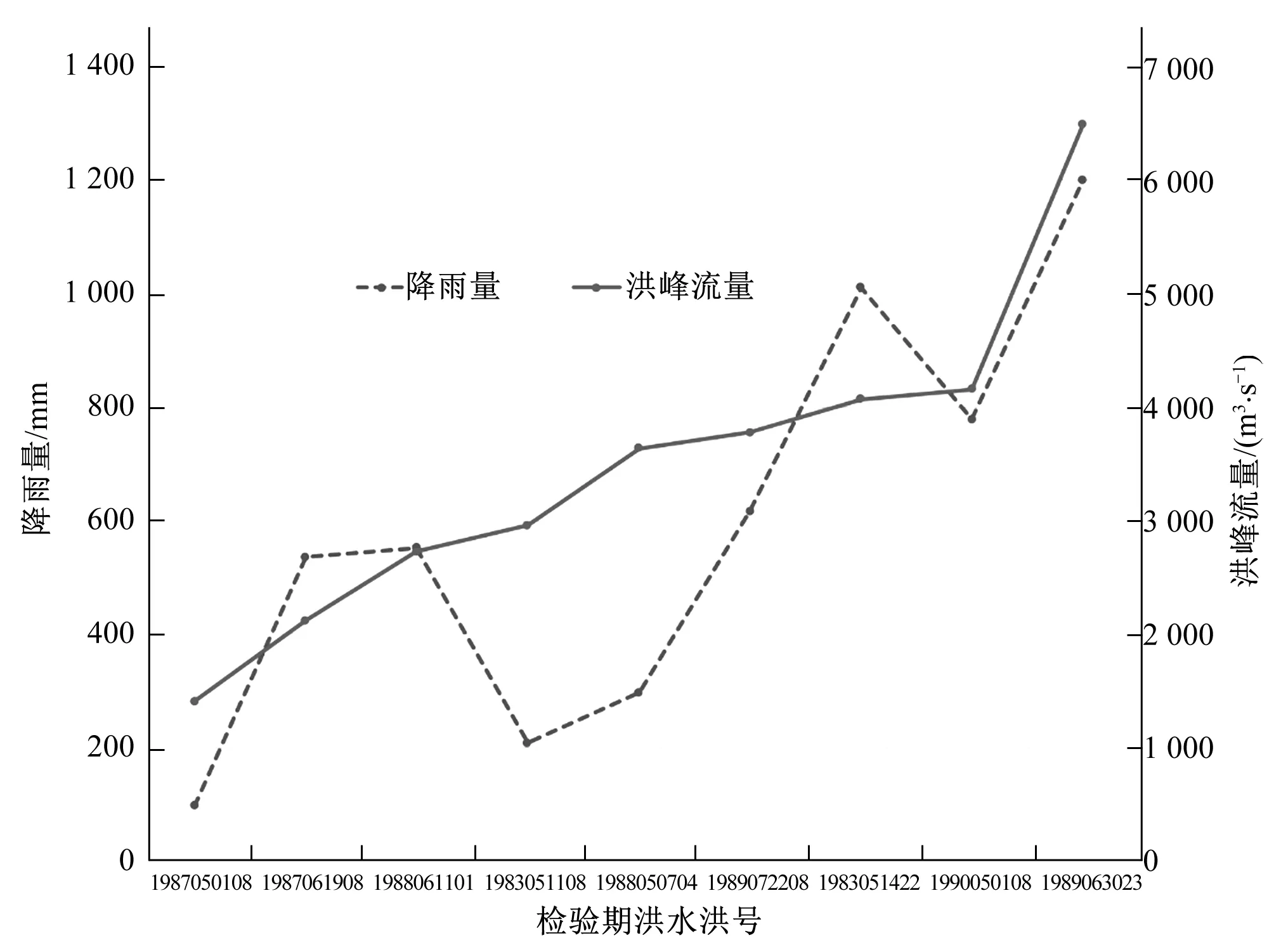
图5 检验期洪水分析Fig.5 Flood analysis of validation period

(3)率定期和检验期洪水代表性。率定期洪水总降雨量的范围是74.2～1 074.4 mm，检验期洪水总降雨量的范围是98.1～1 199.9 mm，率定期和检验期降雨量的量级和范围基本一致，率定期和检验期降雨资料的代表性和一致性较好。率定期洪水洪峰流量的范围是633～4 700 m3/s，检验期洪水洪峰流量的范围是1 410～6 490 m3/s。检验期洪水的洪峰流量大于率定期洪水的洪峰流量，这是为了考察模型对于率定期数据范围外的洪水的预报能力，即考察模型的外推预报能力而进行的设置。这种设置能够考察预报模型对于未曾训练过的大洪水是否具有较好的预报能力，对于模型的实际应用十分有益。

4 结 论

基于ANN和KNN算法，本文构建了一种新型耦合机器学习模型，并用于洪水预报。该模型通过独特的建模方式将ANN与KNN方法相耦合，利用多目标遗传算法和Levenberg-Marquardt算法进行训练，较好地解决了传统ANN模型预见期仅为一个计算时段长、ANN拓扑结构和参数难以同时优化、ANN训练局部极小、单个ANN预报能力不佳等问题。在屯溪流域洪水预报中的应用表明，耦合机器学习模型的精度和可靠性较好，具有较好的应用前景。主要结论如下：

(1)耦合机器学习模型独特的建模方式避免了使用实测前期径流量数据，转而使用模拟前期径流量进行替代，在保证预报精度没有明显衰减的前提下有效增长了模型外推预报的时段数，给延长数据驱动模型预见期提供了新的手段，解决了传统数据驱动模型仅能进行一个时段外推预报的问题。

(2)通过采用特殊的编码方式将网络结构和参数编码为一组决策变量，实现了同时优化网络结构和参数，与多目标全局优化算法的结合改善了网络训练的局部极小问题。

(3)通过耦合ANN和KNN算法，进行取长补短，有效提升了模型预报能力，对于训练期未接触过的大洪水，在检验期预报中仍能取得较为理想的预报精度。

(4)因模型结构较为复杂，计算流程繁多，还存在计算量过大，训练速度较慢的不足，考虑未来采用并行计算技术进行加速，是下一步研究的目标。

□