城门洞型隧洞明满流水力瞬变计算研究

鞠 铖，鞠小明,2，孙立成

(1.四川大学水利水电学院，成都 610065；2.四川大学水力学与山区河流开发保护国家重点实验室，成都 610065)

0 引 言

城门洞型尾水隧洞在水电站输水系统中应用广泛，受到下游运行水位变化的影响，有些水电站尾水隧洞中可能会出现名满交替水流现象，例如当下游水位接近洞顶高程，机组增加负荷，原本是无压流状态的尾水隧洞中可能出现涌波，从而发生有压流和无压流(也称明流)交替流动，对于顶部通气条件不良的城门洞型隧洞，明满流发生时可能还会封存部分气腔在隧洞顶部[1]。实验研究发现明满流发生时，隧洞顶部压力会突然升高或降低，压力变化剧烈， 若设计控制不良可能会影响输水隧洞运行安全[1,2]。对输水隧洞明满流进行水力瞬变计算研究，目的是确定洞顶压力变化值以及变化过程，为输水隧洞设计和运行提供技术依据。由于有压流的水力瞬变方程组和无压流水力瞬变的方程组不同，因此在明满流水力瞬变计算方法上，通常采用两种计算途径，一是将无压流和有压流分开计算，各自采用对应的瞬变流方程组进行求解，将无压流和有压流交界面作为一个滑动的激波来处理，这种方法也称为激波拟合法[3,4]。另一种方法是基于普雷斯曼(Preissmann)窄缝概念，也就是当无压流变成满流时，假想隧洞顶部有一个既不增加过流断面积也不改变过水断面湿周的窄缝，此时的有压流断面隧洞顶部压力就是窄缝中的水深，这样就可以采用无压流瞬变流方程组(圣维南方程组)来求解有压流的断面压力和流量，这样的方法也称为窄缝法或激波捕捉法[5,3]。比较而言，窄缝法比激波拟合法更加实用，在城市污水管网和水电站输水管道的水力瞬变模拟中得到了应用[6～10]。对于城门洞型输水隧洞，即使采用窄缝法进行计算，由于水位处于拱顶部位时的计算变量如面积和湿周等不仅与水深有关，还与自由水面形成的拱顶夹角有关，这使得城门洞型隧洞水力瞬变计算更加复杂和不容易稳定，因此研究城门洞型输水隧洞的水力瞬变方法既有理论指导意义又有现实应用价值。

1 数学模型和基本方程

1.1 有压流水力瞬变计算基本方程和求解方法

有压流水力瞬变计算的基本方程见下式。

运动方程：

(1)

连续方程：

(2)

式中：H为压头；V为流速；x为从管段左端起算的距离；g为重力加速度；f为沿程损失系数；D为管径；a为水锤波速；t为时间。

将基本方程沿正特征线和负特征线分别积分可得正负特征方程，利用边界条件就可以求解有压流隧洞各断面节点的压力值和流量值。

1.2 无压流基本方程和求解方法

无压流水力瞬变计算的基本方程。

运动方程：

(3)

连续方程：

(4)

式中：y为无压流水深；V和t意义同前；A为无压流过水断面积；B为无压流水面宽；S0为无压流隧洞底坡；Sf为无压流阻力损失引起的能量坡度， 由下式计算：

方程(3)和(4)也称为无压流瞬变流计算圣维南(Saint-Venanf)方程组，式中Sf由公式(5)计算。

(5)

式中：n为曼宁粗糙度系数；R为水力半径，由公式(6)计算：

(6)

式中：X为无压流过水断面湿周。

明流水力瞬变计算方法主要有差分法、特征线法、瞬时流态法、微幅波理论法等，其中差分法又分为显式差分法和隐式差分法。也可以将差分法和特征线法结合起来使用，即在边界上采用特征线法，内部断面采用差分法，这样的方法Chaudhry M H称之为扩散法(diffusive scheme)[5]。无论采用哪种计算方法，在无压流瞬变过程中的边界条件方程和计算稳定性都是无法回避和必须考虑的重要问题，有关明流计算方法、差分格式、2维计算方法等可参考有关文献资料[11～14]。

在城门洞型隧洞明流计算中，当瞬时水深超过城门洞直墙高度进入弧形顶拱时，瞬时水面宽度、湿周和过水面积、无压流波速等不仅是瞬时水深yp的函数，同时还是水面扇形瞬时夹角θ的函数，如图1所示，相应的偏导数项将增加一个水面夹角变量，这也是城门洞型隧洞水力瞬变过程计算更加复杂的原因之一。

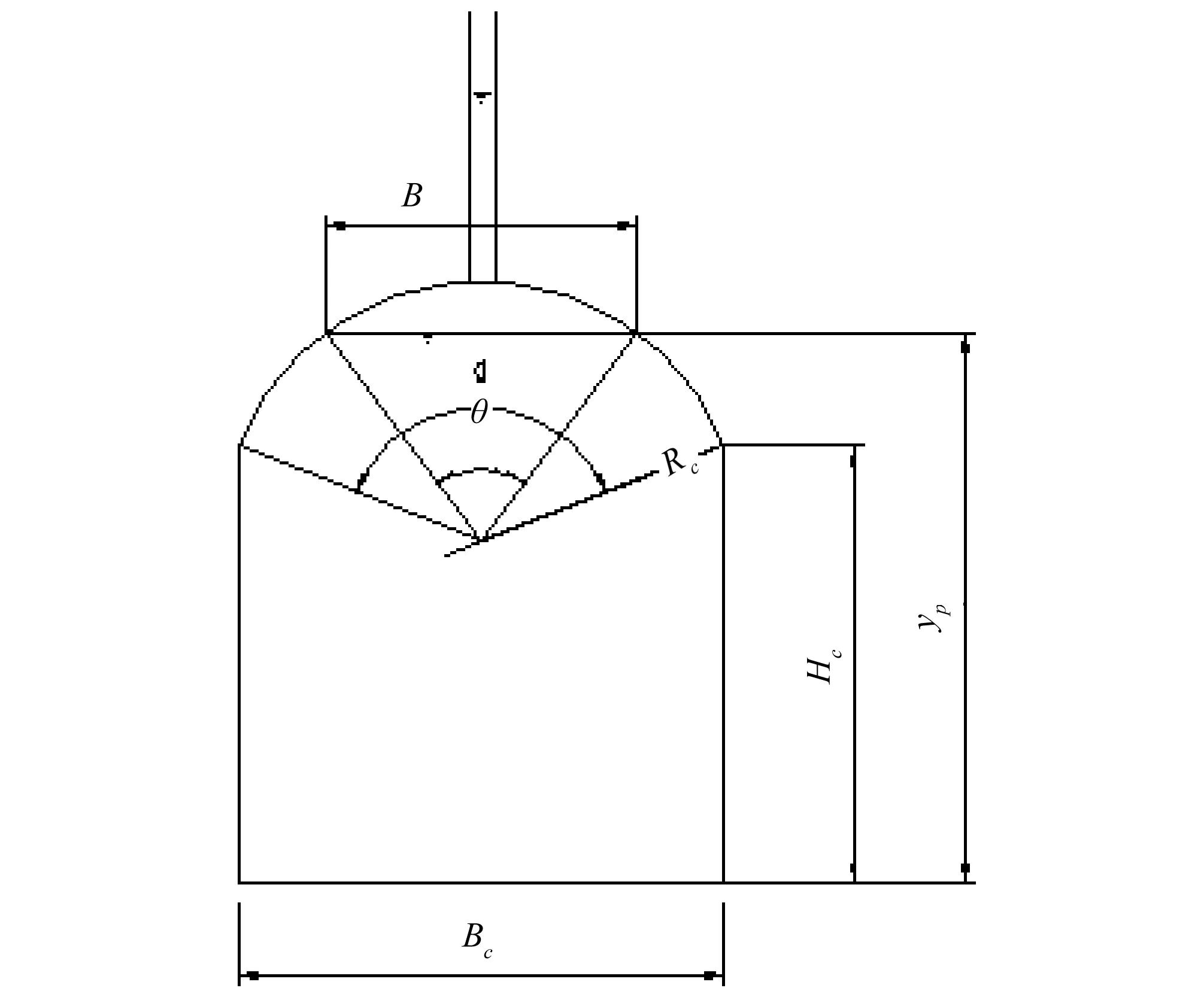
图1 窄缝法计算城门洞隧洞断面图Fig.1 Section of rectangular tunnel with arch crown and a slot

下列公式(7)～(10)用于计算无压流水位超过直墙高度位于弧形顶拱部位时的明流瞬时变量。

扇形水面夹角θ由下式计算：

(7)

式中：yP为隧洞瞬时水深；Hc为城门洞隧洞直墙高度；Rc为城门洞隧洞拱顶半径；Bc为城门洞隧洞底宽。

瞬时水面宽由下式计算：

(8)

式中：θ为扇形水面夹角；其他符号意义同前。

瞬时湿周由下式计算：

X=Bc+2Hc+Rc(α-θ)

(9)

式中：α为城门洞拱顶夹角(弧度)；其他符号意义同前。

瞬时过水面积由下式计算：

(10)

式中：A为城门洞隧洞瞬时过水断面积；其他符号意义同前。

城门洞型隧洞水力瞬变计算时需要知道系统内所有断面上的初始恒定状态，即需要知道每一节点处的水深和流速，无压明流隧洞初始水面曲线可由明渠渐变流常微分方程计算确定[5]。

(11)

式中：Q为隧洞明流过流量；其他符号意义同前。

用四阶龙格-库塔法求解上述方程，已知X=Xi处水深为yi，那么X=Xi+1处水深为：

(12)

式中：

a1=Δxf(xi,yi)

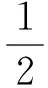
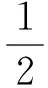
a4=Δxf(xi+Δx,yi+a3)

隧洞内明流各断面的初始水位可由上述方程(11)和(12)计算确定。

2 普雷斯曼窄缝法计算明满流水力瞬变方法

2.1 普雷斯曼(Preissmann)窄缝法计算原理

当城门洞隧洞出口水位接近洞顶高程时，若隧洞内水流发生水力瞬变，此时就可能发生明满流现象(也称明满交替水流)。普雷斯曼(Preissmann)提出了一个有趣的计算方法，该方法假想隧洞内水流由无压流转变为有压流时，隧洞顶部通气良好，不存在封存气囊或气腔，并假想隧洞顶部存在一个窄缝(参见图1)，该窄缝既不增加过流断面积，也不增加水力半径，当发生有压流时，只要满足无压流波速(celerity of surface wave)与有压流水锤波速(velocity of water-hammer)相等的方法来选择窄缝宽度[15,,5]，这样窄缝中的水深变量就是有压流的压力水头变量，并且物理概念也完全一致，如此无压流和有压流就可以用同一形式的圣维南方程组来描述，求解这个方程就可以进行明满流水力瞬变的计算，这就是明满流水力瞬变计算的基本原理和方法，该方法在城市下水道的水力瞬变计算中得到了应用。由于该方法没有考虑城门洞洞顶可能存在的气囊或气腔内空气体积的变化，仅适用于洞顶通气条件良好的隧洞，本文采用窄缝法的基本思路和原理对城门洞型输水隧洞进行水力瞬变计算研究。

2.2 城门洞隧洞明满流算例

某大型发电输水尾水隧洞采用城门洞型断面，隧洞底宽17.5 m，直墙高17.04 m，顶拱夹角118.15°，隧洞断面最大净空高度22.0 m，隧洞长300.0 m，底坡0.00，如图2所示。由于隧洞断面尺寸大，不具备采用变顶高的通气和排气隧洞条件，当电站尾水水位接近洞顶高程附近时，此时上游断面流量增加，隧洞内将产生明满交替水流；或者隧洞内原为有压流动，当上游断面流量减小，也将产生明满交替水流。

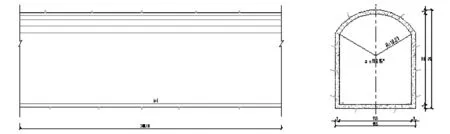
图2 某输水隧洞布置图Fig.2 Profile of an engineering tunnel with arch crown

采用前述的计算原理和计算方法，隧洞全长300 m，共分为50段，也即6 m一小段，包括首尾共有51个计算节点。为了能够观察隧洞全长范围内不同断面的水力瞬变情况，并且两个观察断面的水力瞬变量能有比较大的区别，方便用不同曲线来表示，从上游0 m断面开始每间隔60 m选择一个观察特征断面，因此分别选取距离上游0、120、240 m三个断面作为计算观察特征断面，研究这些特征断面发生明满流时的水深变化过程，而隧洞下游出口断面始终保持初始恒定状态的水深。计算三种发生明满流的工况，如表1所示。

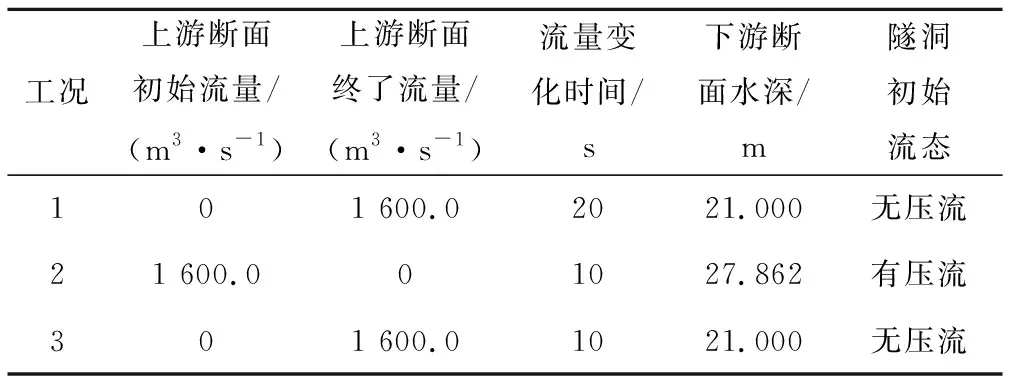
表1 发生明满流的计算工况Tab.1 Free-surface-pressure flow transient condition of calculation

工况1是隧洞内初始流量为0，下游断面水深21.0 m，距离洞顶1.0 m，隧洞内初始状态为无压流，隧洞上游断面流量在20 s内线性增加至1 600 m3/s，隧洞内各断面水深变化过程如图3所示。工况2是下游断面水深27.862 m，超过洞顶5.862 m，初始工况是有压流，初始流量1 600 m3/s，上游断面在10 s内流量线性减小至零，隧洞内各特征断面的水深变化如图4所示。工况3是将第一种工况的流量变化时间缩短为10 s，隧洞内各特征断面的水深变化如图5所示。

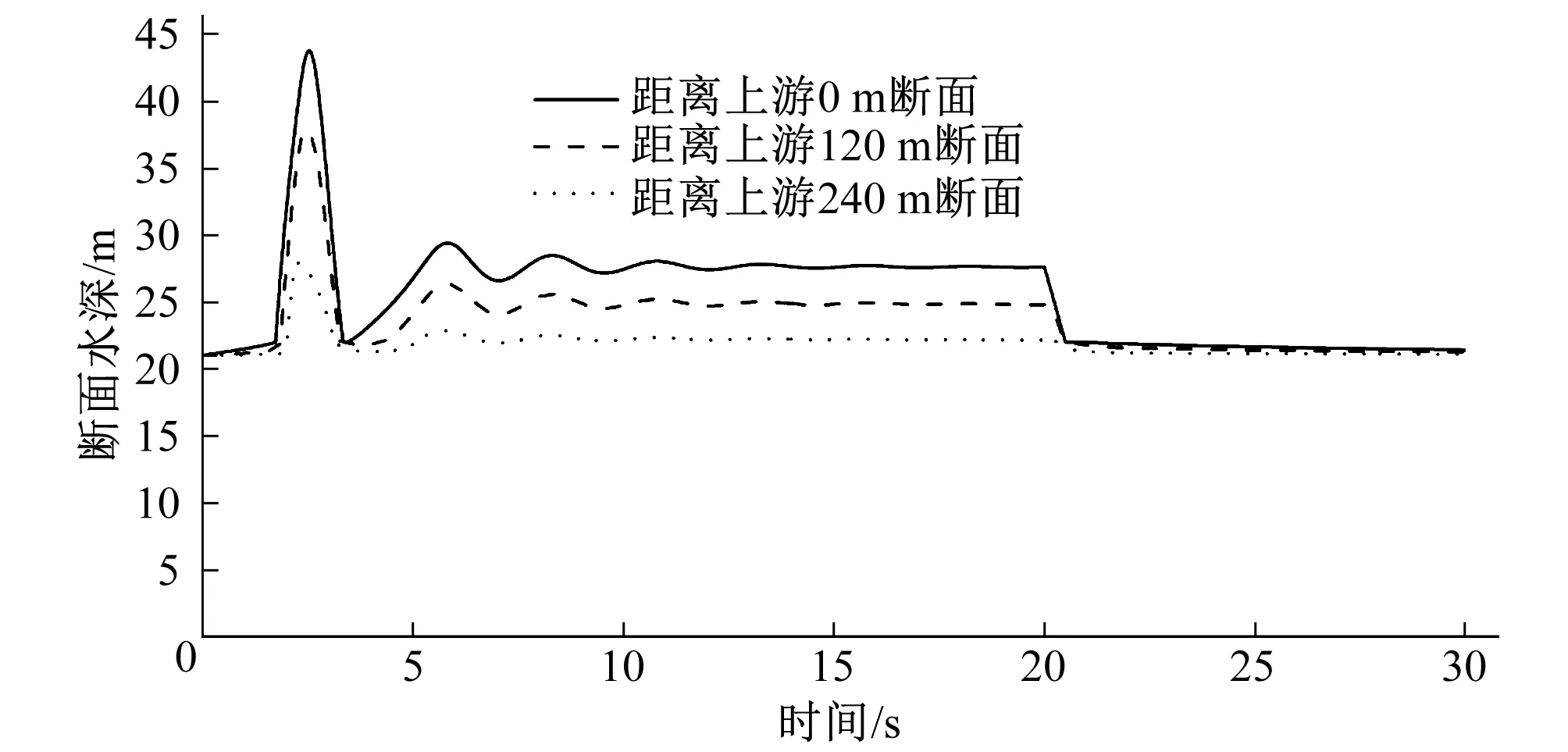
图3 上游断面流量增加特征断面水深变化过程(工况1)Fig.3 Process of water depth variation on particular section with flow discharge increasing upstream (condition 1)

图4 上游断面流量减小特征断面水深变化过程(工况2)Fig.4 Process of water depth variation on particular section with flow discharge decreasing upstream (condition 2)

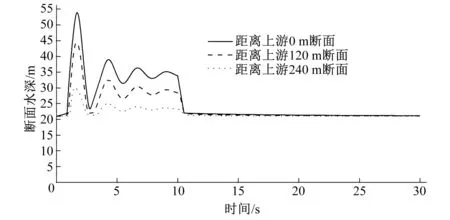
图5 上游断面流量增加特征断面水深变化过程(工况3)Fig.5 Process of water depth variation on particular section with flow discharge increasing upstream (condition 3)

2.3 算例计算成果分析

从工况1的计算成果图3可以看出，隧洞初始状态为无压流，随着上游断面流量增加，在上游流量开始变化后的1.74 s首先是上游第一个断面(距离上游0 m断面)变成有压流，随后隧洞处于有压流状态，并且当从无压流变为有压流时，隧洞水深(拱顶压力)急剧变化，之后维持一段时间的有压流状态，当上游断面流量增加结束，不再有补充流量时，隧洞内水流恢复无压状态，从图中可以看出距离流量变化断面越近，压力变化越大，图3中距离上游0 m断面窄缝内最大水深43.755 m,算例隧洞最大净高22.0 m，相当于顶拱在明满交替时压力剧变21.755 m，这种剧变压力类似于水锤压力，是瞬间产生的，它不同于静水压强分布规律，对隧洞顶部的衬砌会造成不利影响，严重时可能会影响衬砌结构安全。图4为初始状态是有压流，上游断面流量减小，可以看出最先是距离上游0 m断面的水深减小，然后是后续断面水深跟着减小，从有压流变为无压流时没有发生压力剧变(模型中不考虑洞顶空气体积变化)，距离上游0 m断面最小水深17.238 m，基本处于城门洞直墙顶高程附近(算例直墙高17.04 m)，也就是水力瞬变处于拱顶变水面宽的穹顶内，说明前述计算方法中关于水位处于穹顶内的计算原理是可行的，随着无压流过渡过程的发展，因为隧洞最下游的断面是有压的(窄缝内水深27.862 m，隧洞净高22.0 m)，因此在流量变化后的11.38 s时刻，首先是靠近下游断面的特征断面出现有压流，如图4中的红色线(图中更靠近下游的虚线最小水位均高于22.0 m，该断面是有压状态)，然后上游断面也开始出现有压流，但是依然是最靠近流量变化断面的节点出现最大水深，如图4中的距离上游0 m断面窄缝内最大水深38.729 m，即明满流交替时压力剧变16.729 m。表2是初始工况是有压流，上游断面流量减小后各特征断面的最大和最小水深。

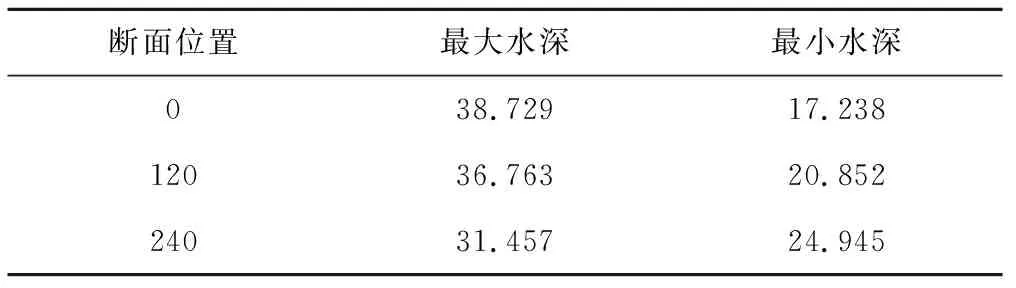
表2 上游断面流量减小各特征断面最大和最小水深 m

图5与图3类似，区别是上游断面流量变化比图3快1倍，窄缝内最大水深达到53.896 m，即明满流交替时压力剧变达到31.896 m，说明流量变化越快，明满流交替产生的压力变化越大，两种情况的拱顶最大压力数据比较如表3所示。

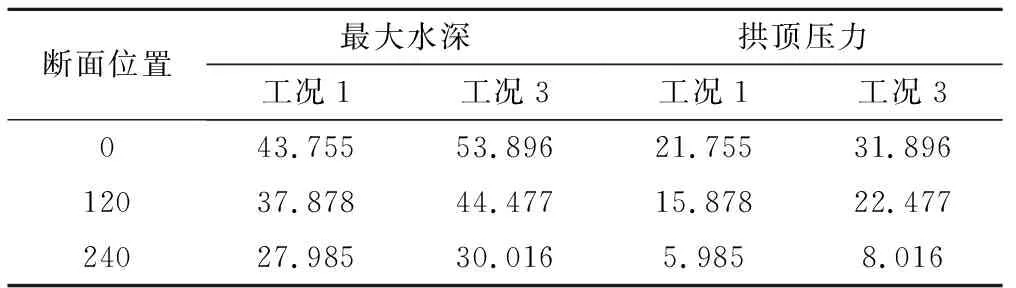
表3 不同流量变化时间各特征断面水深和拱顶压力比较(工况1/工况3) m

3 结 语

算例研究表明采用窄缝法计算城门洞型隧洞内的明满交替水力瞬变过程是可行的；在不考虑洞顶可能存在的气囊或气腔内空气体积变化的情形下，隧洞内水流由无压流变为有压流时将产生较大的压力变化，由有压流变为无压流时压力变化较小；隧洞内断面流量变化越快，明满流交替产生的压力变化也越大；靠近流量变化越近的断面水力瞬变程度越急剧。

□