基于CFD无网格算法的飞行器电磁隐身特性模拟

高煜堃，陈红全，王 彪，吴 浩，胡晓磊，宋强强

(1.安徽工业大学机械工程学院，安徽马鞍山243002；2.南京航空航天大学航空宇航学院，江苏南京 210016)

关于现代先进军用飞行器电磁隐身特性的研究一直是学术界和工程界关注的热点问题。雷达散射截面(radar cross section，RCS)作为评价飞行器电磁隐身特性的一项重要指标，通常通过求解麦克斯韦方程获得。随着计算机水平的不断提高，越来越多的研究者开始尝试采用数值方法来求解麦克斯韦方程，获取目标RCS。传统的数值方法有时域有限差分法[1]、间断有限元法[2]、时域有限体积法[3-4]和时域有限元法[5]等，这些方法均依赖于网格单元离散计算域，受到网格化的约束。无网格方法打破了传统网格方法受到的网格化约束，其计算域的离散只涉及布点，不需生成网格单元，实施灵活，适合于处理多体干扰及多部件干扰等复杂情形问题。

目前，已有研究者尝试采用无网格方法进行电磁场数值计算，其中典型的有无单元Galerkin方法[6]和径向基函数的无网格方法[7]。上述两类无网格求解方法均与基函数(或形函数)的选取相关，基函数的选取不仅会影响矩阵求逆运算中涉及的逆矩阵质量，进而影响算法的收敛性；而且会影响到边界条件的处理，有时边界条件需采用特殊的方法强制给定。在计算流体力学(computational fluid dynamics，CFD)领域，近年来出现了一种用于求解欧拉方程的无网格方法[8],其空间离散不涉及基函数的选取，避免了逆矩阵对算法收敛性的影响，边界条件的施加也相对简单，通用性较好。基于此，笔者借鉴CFD无网格方法的思想，提出一种基于CFD的时域无网格算法，用于求解麦克斯韦方程，采用Steger-Warming通量分裂进行通量计算，且采用本文算法对文献[9]中的平板飞机模型进行电磁隐身特性模拟。

1 基于CFD的时域无网格算法

1.1 控制方程

对于横磁(transverse magnetic，TM)波，在直角坐标系中，守恒型量纲为一的时域麦克斯韦方程[10]可写为

其中：W=[εEzμHxμHy]T；F1=[-Hy0 -Ez]T；F2=[HxEz0]T；S=[-σEz-σmHx-σmHy]T；Ez为电场强度E在z方向上的分量；Hx和Hy分别为磁场强度H在x和y方向上的分量；ε为介电常数；μ为磁导率；σ为电导率；σm为磁阻率。

1.2 计算区域布点及点云生成

与传统的网格方法不同，无网格方法计算区域的离散只涉及布点而不需生成网格单元，通常情况下，既可直接采用网格点对计算域进行离散，也可根据需要进行布点离散计算域。对计算域布点离散后需生成局部点云结构。以点云Ci为例(见图1)，文献[11]中给出了点云Ci的具体生成方法。其中点i为点云Ci的中心点，点1～6为点云Ci的卫星点。

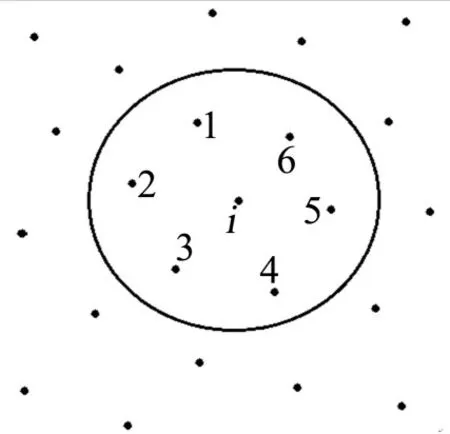
图1 点云Ci示意图Fig.1 Schematic diagram of cloud of pointsCi

1.3 空间导数逼近

在点云Ci上，假设中心点i附近的函数分布f=f(x,y)和连续可微，那么f可用i处的函数值fi=f(xi,yi)通过泰勒级数展开逼近

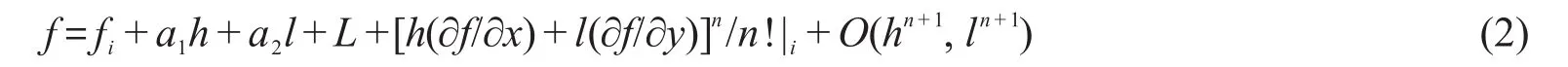
其中：h=x-xi；h=y-yi；ai(i=1,2)为函数f在中心点i处的空间导数。对于线性逼近，式(2)函数的近似值可写为fˉ=fi+a1h+a2l。对于时域无网格算法，卫星点k(k=1,…,M)处的函数值为已知，记作fk。为使卫星点处函数值的线性逼近总体误差取到极小值，则空间导数满足下式[11]

那么线性逼近函数可整理为f(x,y)=fi+∑αk(fk-fi)h+βk(fk-fi)l，其中系数αk和βk仅与离散点坐标相关，在时间推进计算前可一次求出。因此，函数f在中心点i处的空间导数可逼近为

空间导数也可用中心点与卫星点连线中点处的函数值进行逼近

其中系数αik和βik在时间推进计算前也可一次求出。

1.4 通量运算

在点云Ci上，运用式(5)，则中心点i处的通量项可写为

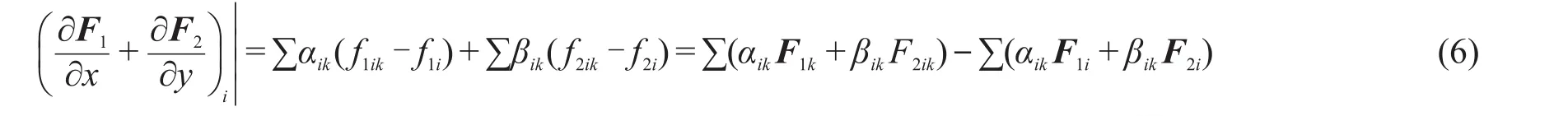
由于求和项 ∑(αikF1k+βikF2i)为已知(系数αik和βik在时间推进计算前已经计算得到，F1i和F2i为计算点处当前的已知值)，在中心点与每一个卫星点连线的中点处建立一个虚拟界面，如图2。并定义一个数值通量Qik=ξikF1(Wik)+ηikF2(Wik)，其中定义矢量dik=(αik，βik）,那么式(6)可写为

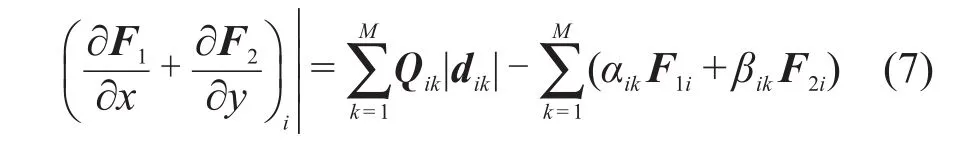
图2 点云Ci中心点与卫星点连线中点处引入的虚拟界面Fig.2 Virtual interface between the central and each satellite point on the point cloud ofCi

为了计算Qik，借鉴CFD的做法，采用Steger-Warming通量分裂方法[4]分裂Qik的雅克比矩阵Tik=∂Qik/∂Wik，那么Qik可写成分裂形式其中为Tik的分裂矩阵，可由线性函数重构得到U+=Ui+0.5∇Ui∙rik，U-=Uk+0.5∇Uk∙rik，其中rik=(xk-xi，yk-yi)，这里U表示W的任意分量，∇Ui和∇Uk可以由式(4)计算得到。

1.5 时间推进与边界条件

空间离散后，在点云Ci上，麦克斯韦方程的半离散形式可写为

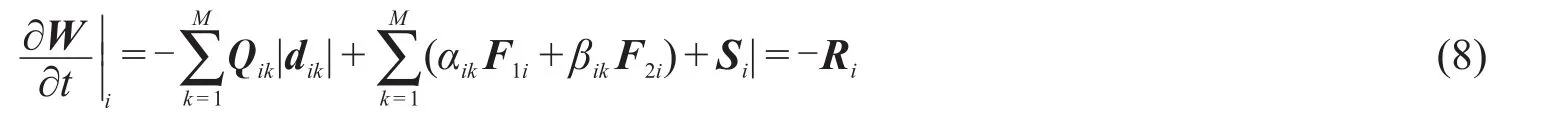
其中Ri为计算点i处的残差。然后按照四步Runge-Kutta方法[4]对式(8)进行时间推进求解。文中物面采用良导体边界条件，截断边界采用完全匹配层边界条件，具体参数取值同文献[4]。

图3 入射波示意图Fig.3 Schematic diagram of incident wave

2 算例及结果分析

算法采用fortran编程实现，并采用该程序对文献[9]中飞机模型的隐身特性进行分析。图3为沿着k′方向传播的TM平面波示意图，定义k′轴与x轴之间的夹角为入射角φ，归一化后的入射波分量可表示为

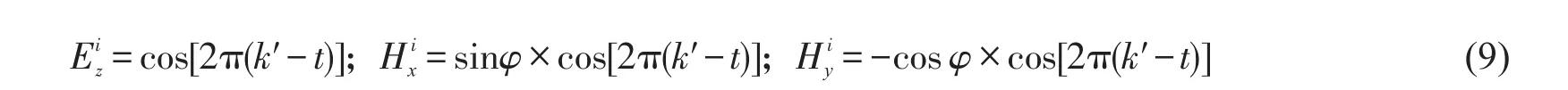
其中k′=xcosφ×ysinφ。算例涉及的计算域中x和y坐标均为以入射波波长λ为特征长度、量纲为一的空间位置。

2.1 二维圆柱散射数值模拟

图4 二维圆柱的散射场分布Fig.4 Distribution of the scattered fields of 2D cylinders

选用二维圆柱算例对本文算法进行验证。数值模拟时，取圆柱半径r=0.5λ，置于10λ×10λ的计算域中，总布点数为14 458，采用沿x轴方向的TM波入射(对应φ=0°)。计算得到的圆柱散射场分布和双站RCS分布分别见图4，5。由图4可知，当电磁波沿x轴方向照射时，双站角0°方向的散射场最强，这与计算得到的双站RCS分布(见图5)一致，RCS最大值出现在双站角0°方向。由图5可知，基于本文算法计算得到的双站RCS分布在整个双站角内都能与级数解[12]吻合。图6为二维圆柱的残值收敛历程。由图6可知，当迭代周期为36时，本文算法的迭代平均残值下降到1.0×107以下，收敛速度良好。

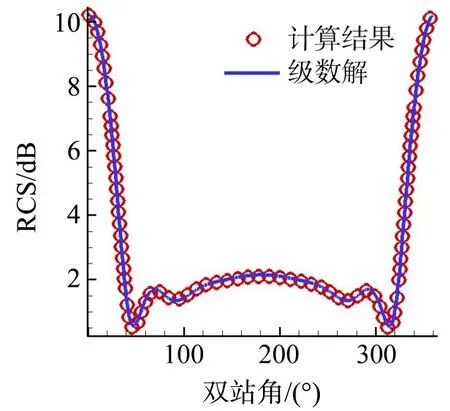
图5 二维圆柱的双站RCS分布Fig.5 Distribution of the bistatic RCS of 2D cylinders

图6 二维圆柱的残值收敛历程Fig.6 Convergence process of the value of 2D cylinders

2.2 平板飞机模型隐身特性模拟

为验证本文算法处理多体及多部件干扰问题的能力，选用文献[9]中的平板飞机模型进行电磁隐身特性模拟。数值模拟时，将两架相同的、长度均为6λ的平板飞机模型并排放置在大小为24λ×24λ的计算域中，见图7，总布点数为46 917。为研究电磁波从不同方向照射时飞机模型的隐身特性，取TM波入射角φ=0°～90°范围内(对应电磁波从飞机模型的侧前方照射)每间隔5°的19种情形，从RCS平均值、最大值以及大于门槛值的概率3个指标来分析飞机模型的隐身特性，根据文献[9]设置RCS门槛值分析RCS隐身特性，文中将该值设置为0 dB，对应计算得到的双站RCS结果见表1。一般来说，RCS平均值越小越好，RCS最大值越小越好，RCS大于门槛值的概率越低越好。

图7 飞机模型计算域布点离散示意图Fig.7 Points distribution in the computational domain for the aircraft models

由表1第四列可知，RCS最大值出现的角度与入射角相同，表明在入射角方向上的散射最强。由表1第二列可知：φ=0°时，RCS平均值最大，为7.427 dB；φ=5°，15°时，RCS平均值较大；φ=50°时，RCS平均值最小，为4.468 dB；φ=65°，90°时，RCS平均值较小。由表1第三列可知：φ=45°时，RCS最大值最大为28.116 dB；φ=30°，35°时，RCS最大值较大；φ=90°时，RCS最大值最小，为26.006 dB；φ=80°，85°时，RCS最大值较小。由表1第五列可知：φ=0°，5°时，RCS大于门槛值的概率最大，为88.1%；φ=50°时，RCS大于门槛值的概率最小，为73.3%；φ=65°，90°时，RCS大于门槛值的概率较小。综合来看：φ=0°时(对应电磁波从正前方照射)，RCS平均值和大于门槛值的概率均最大，隐身特性较差；φ=90°时(对应电磁波从侧向照射)，RCS平均值、最大值以及大于门槛值的概率均较小，隐身特性较好。

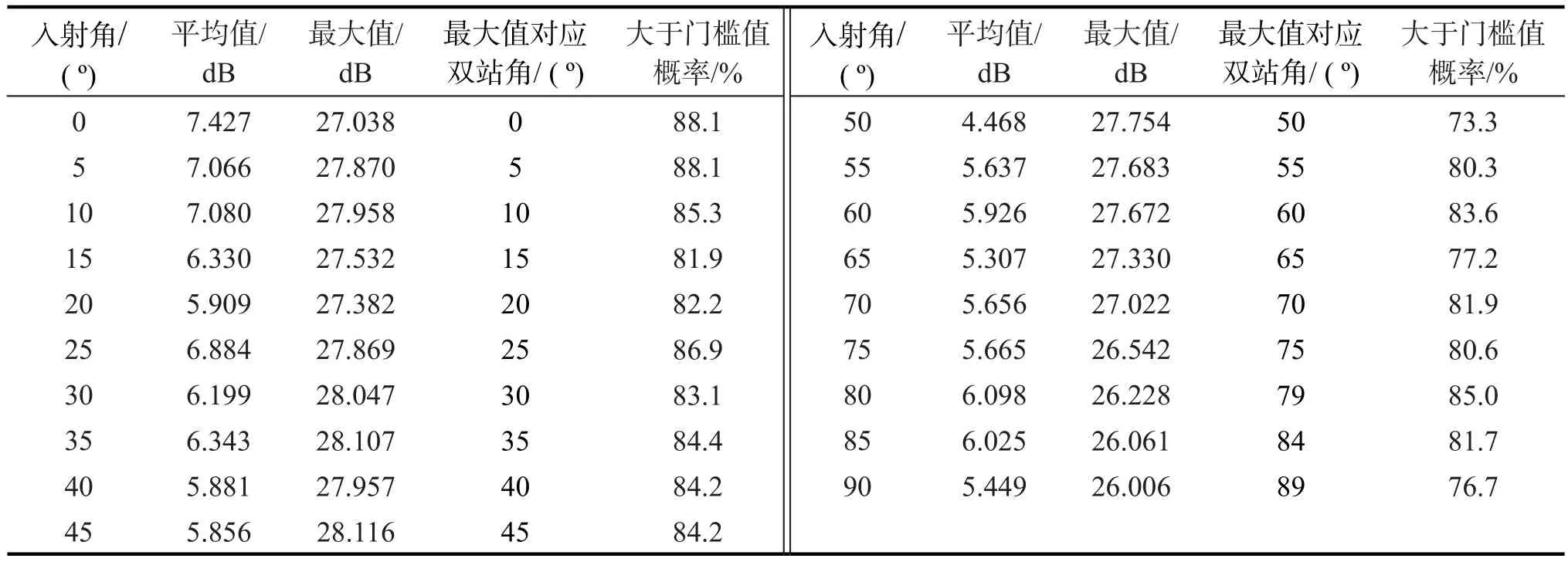
表1 飞机模型不同入射角情形对应的双站RCS分析Tab.1 Analysis of the bistatic RCS of aircraft models with different incident angles

图8 飞机模型散射场分布Fig.8 Distribution of the scattered fields of aircraft models

图8，9分别为飞机模型在φ=0°和φ=90°情形下散射场分布和双站RCS分布。由图8可知：当电磁波从正前方照射飞机模型时(φ=0°)，尾翼被机翼遮挡，机翼之前的外形布局部件间二面角均大于90°,可有效回避散射波的叠加，表现为各部件产生的散射波在散射场中有序发散传播(图8(a))，最强散射出现在双站角0°方向，这与图9中的RCS分布一致；当电磁波从侧向照射飞机模型时(φ=90°)，机头与机身、机身与机翼以及机身与尾翼之间都存在一定的电磁散射干扰，在双站角180°～360°范围内最强散射方向上的散射强度被削弱，故在整个双站角范围内最强散射只出现在90°方向上(图8(b))，这也与图9中的RCS分布吻合。

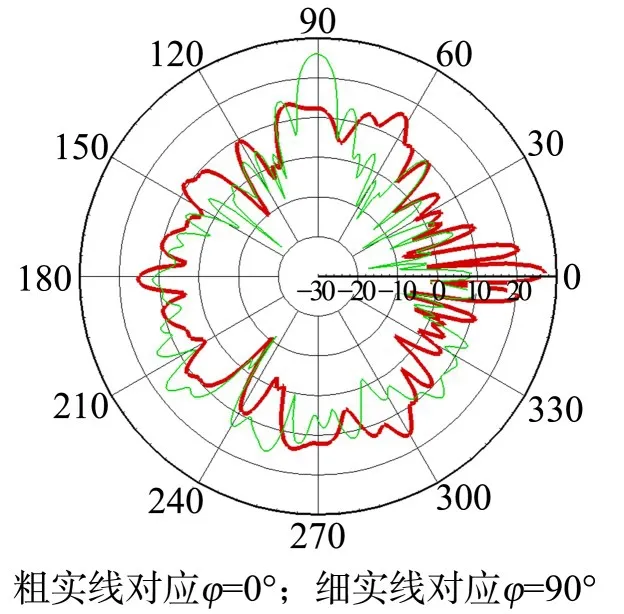
图9 飞机模型双站RCS分布Fig.9 Distribution of the bistatic RCS of aircraft models

3 结 论

借鉴CFD中Steger-Warming通量分裂方法，提出基于CFD的时域无网格算法，并用于分析飞行器的电磁隐身特性，结论如下：

1)采用本文算法计算得到的二维圆柱双站RCS能与级数解吻合；

2)从RCS平均值、最大值以及大于门槛值的概率三方面综合分析飞机模型的隐身特性，当入射角φ=0°时(对应电磁波从正前方照射)飞机隐身特性较差，而当入射角φ=90°时(对应电磁波从侧向照射)飞机隐身特性较好，这与散射场的叠加作用以及飞机外形等因素有关；

3)本文算法基于无网格点云构造，适合于处理多体及多部件目标等电磁散射干扰问题。