基于全参数化建模的多用途船型线优化设计
,,,,
(中远海运重工有限公司,辽宁 大连 116600)
多用途船是继油船、散货船及集装箱船三大主力船型之后市场需求最大的第四大船型,航运市场对多用途船的需求在不断增加,而船舶型线设计直接影响其航行性能和营运经济性。传统的型线优化设计均在母型船的基础上进行改良,包括基于势流的兴波阻力优化[1]、基于黏流的船艉型线优化[2-3]、以及基于船模试验的型线对比及节能装置对比等[4],而多用途船的载货种类、载货方式、航线等均有较大差异,基于母型船的设计不但会限制其布置方案,还会影响航行性能。此外,针对肥大船型的型线优化目前已不再局限于减小静水阻力,其艉部型线对伴流场影响也越来越受到关注。为此,考虑在满足多用途船布置要求的基础上,通过编写Feature语句实现船型的全参数化建模,采用多种优化算法分别针对船艉、船艏及全船进行船型优化。基于高精度黏性求解器,对比分析实尺度下的船舶航行阻力及伴流目标函数,避免尺度效应对船型设计的影响,完成多用途船的型线优化设计。
1 优化方法及计算原理
在无母型船参考的条件下,型线优化采用渐进逐步逼近法,即选定优化参数后,首先给定大的搜索范围,根据计算结果逐步缩小搜索区域,直到确定最优的参数值为止。优化流程见图1,优化循环示意见图2。
选用的主要算法如下。
1)Sobol算法。一种伪随机算法,相对于传统的随机算法,其产生的初始设计点在空间上分布得更加均匀。
2)NSGA II带精英策略的遗传算法。核心优化算法,解决了计算程序复杂、个别计算系数的选取较为依赖经验等不足,大大提高了算法的性能[5-6]。
3)Exhaustive Search算法、T-Search递进算法。很小范围内,逐个递进搜索法。
1.1 静水阻力计算原理
为避免由模型尺度效应带来的误差,优化过程中的静水阻力计算采用实尺度模型直接计算,通过高精度黏性求解器得到。
湍流模型为时均方法中的Realizablek-ε模型[8],湍动能k和湍动耗散率ε的输运方程如下。
(1)
(2)
相比于标准k-ε模型,Realizablek-ε模型更新了耗散率ε的输运方程,方程中的产生项不再包含Gk,且最后一项不具有任何奇异性,即使k值很小或为0,分母也不会为0。此外,标准k-ε模型中假定粘度系数Cμ=0.09,即各项同性的标量,而实际弯曲流线的情况下湍流是各项异性的,因此Realizablek-ε模型中将黏度系数与应变率联系起来,更适合模拟强旋流。
(3)
1.2 伴流目标函数计算原理
在船舶型线设计阶段,由于没有母型船进行参考,其螺旋桨推进效率无法准确估算。故采用伴流目标函数WOF(Wake Object Function)来评判伴流场的优劣。
(4)

2 数值验证与分析
以5万t多用途船型线优化为例,其主尺度信息及优化限制条件见表1,优化工况仅一个航速工况点:吃水12.5 m,航速14 kn。
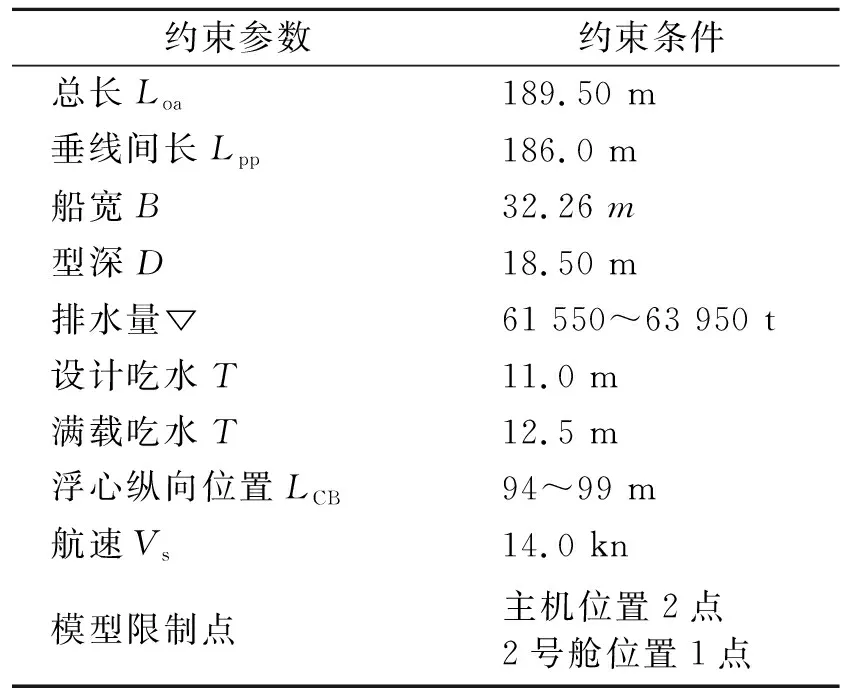
表1 多用途船主尺度及约束条件
根据总布置图及模型限制点,建立船型参数控制曲线,见图3。
控制曲线包括艏、艉平边线、平底线、设计水线、甲板边线、水线外飘角度线、甲板外飘角度线、横剖面面积曲线、尾轴轮廓线、中纵剖线等。每条控制线均由点坐标、切线角度、丰盈度系数或面积控制,各控制参数均可作为优化参数进行优化,本项目中的优化参数共计57个。
根据上述布置条件,设计得到初版多用途船船体型线,其三维模型见图4。
设计采用直艏形式,水线以下部分的横剖面以U形为主,进流段水线较瘦,在保证平行中体长度的同时增加艉部去流段长度。
由表1知,优化工况对应的Fr数为0.168,属于低速。当船舶排水量不变时,摩擦阻力优化空间较小,而船艉去流段主要影响黏压阻力,艏部形状主要影响船艏兴波及艏部压力分布。
基于以上考量,多用途船的型线优化将采用3轮优化策略:首先优化船艉形状,以减小占比较大的粘压阻力;其次,优化艏部形状,改善艏部兴波以及船身横波的分布;最后,检查约束条件,进行艏、艉更精细的优化,得到最终优化型线。不同算法下每轮优化的案例数见表2。
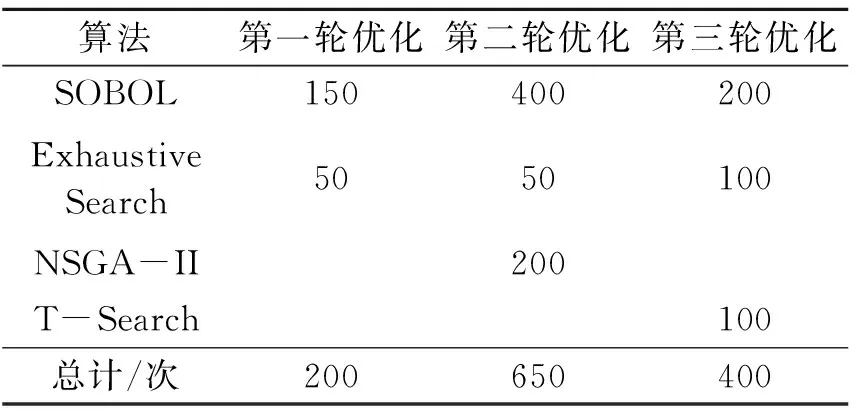
表2 多用途船3轮优化案例数表
由于船舶左右对称,为提高计算效率,采用半船模型模拟计算,其计算域及网格划分见图5。
2.1 第一轮优化
仅优化船舶艉部,采用高精度黏性求解器计算得到不同船型的静水阻力以及对应艉部压力分布,得到的船型其艏部与初版型线相同,艉部型线对比见图6。
相比于初版型线,第一轮优化船型船艉兴波几乎不变,但其压力分布改善较多,尤其是低压区,见图7。总阻力较初版船型减小2.25%,剩余阻力减小5.94%。
2.2 第二轮优化
采用第一轮优化后的船艉,仅优化船艏(见图8)。借助势流求解器,快速预测不同船型的兴波阻力系数,筛选优化过程中的船型,经过高精度黏性求解器计算,对比航行阻力,得到最佳船型。
与初版型线相比,优化后的船型其隐形球艏部分更加明显,水线以下的横剖面线更偏U形。
12.5 m吃水14 kn航速下第二轮船艏优化型线与初版型线的兴波对比见图9,船身波高对比见图10,相比于初版型线,优化后的船艏其艏波谷向前移动,同时船身周围几乎无横波,兴波阻力系数明显减小,较第一轮型线总阻力减小2.58%,剩余阻力减小12.13%。
2.3 第三轮优化
全船优化,在检查约束条件的基础上,针对艏、艉线型进行更精细的优化,以自动优化算法辅助手动优化完成本轮型线优化,型线对比见图11。
对比第一轮优化型线,第三轮优化得到的型线其艉部高压区明显向船首方向移动,且压力变化均匀、缓和,逆压梯度较小,见图12,因而粘压阻力最优。
对比3轮优化船型的自由液面兴波波形见图13,对比3轮优化船型的船身波高见图14。可以看出,经过第三轮优化算法结合手动优化,对比第二轮优化型线,在船身附近几乎无横波的基础上,减小了散波,同时,艉波峰值明显减小,有效降低了兴波阻力。
对比3轮优化型线在12.5 m吃水14 kn航速下的总阻力见表3。在整个优化过程中,由于排水体积限制,其摩擦阻力几乎不变,第三轮优化型线较初版型线总阻力减小6.35%,剩余阻力(包括粘压阻力与兴波阻力)减小24.51%,剩余阻力占总阻力比例仅为19.82%。
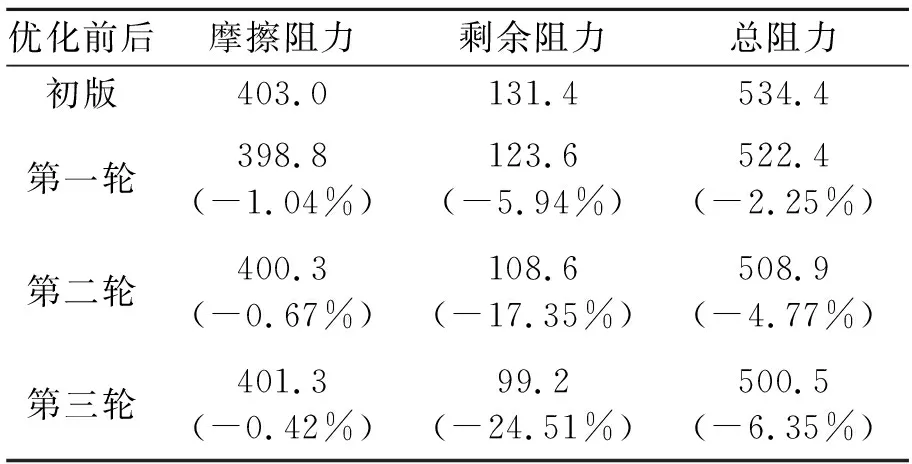
表3 三轮优化方案总阻力对比 kN
2.4 伴流目标函数对比分析
船艉型线优化除了减小黏压阻力外,还应减小伴流目标函数WOF值,以改善船艉伴流,提高螺旋桨推进效率。桨盘速度点提取见图15,圆柱坐标系位于桨盘中心处,r从0.6R~1.0R,间隔0.1R;φ从0°~350°,间隔10°。
对应伴流目标函数计算结果见表4。相比于初版型线,第一轮优化型线其艉部伴流场变化不大,低速区面积略微减小,其0.6R~1.0R处的平均伴流分数变化较大,伴流目标函数WOF值较初版型线仅减小0.63%;而第三轮优化型线的艉部伴流场有明显改善,其低速区面积明显减小,低速值增大,0.6R~1.0R处的平均伴流分数均小于初版型线与第一轮优化型线,即各个半径上的平均速度较大,计算得到的伴流目标函数WOF值为0.667 0,较初版型线WOF减小8.6%,其伴流场更加均匀。
综上,优化后的船型不但可满足布置要求,其静水阻力与伴流目标函数值分别降低6.35%与8.6%,在相同航速下,主机功率更小,有效提高了航行性能与营运经济性。
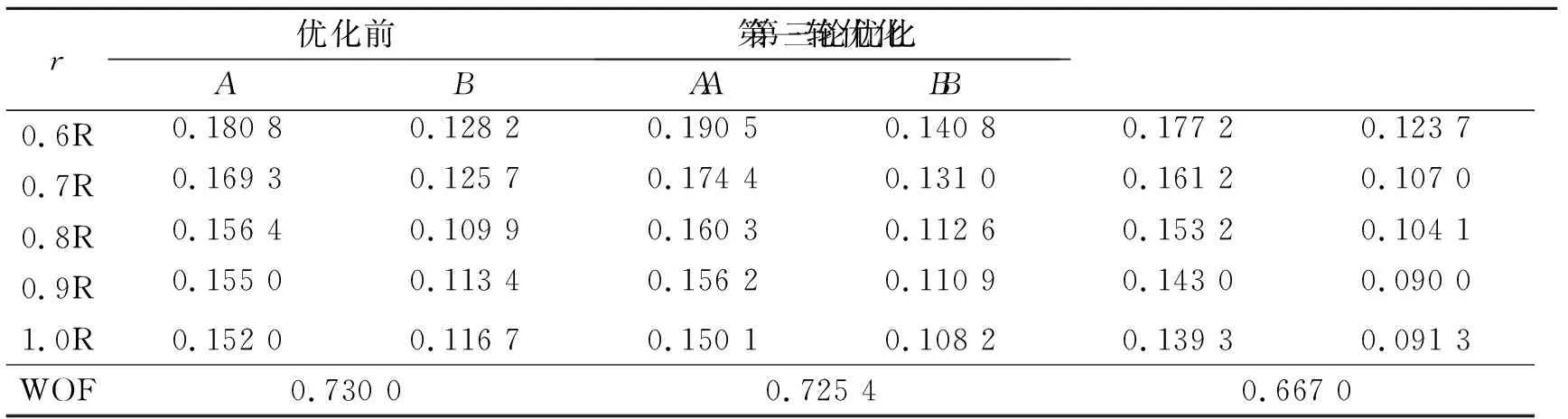
表4 伴流目标函数计算结果
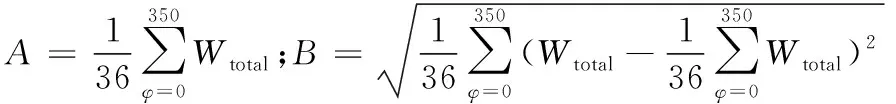
3 结论
1)全参数化建模在保证模型光顺下,可实现快速变化的能力,与多种优化算法共同优化大幅缩短了船型设计时间,在满足布置要求基础上,优化得到性能良好的船型。
2)低速肥大船型的总阻力中剩余阻力占比较小,而剩余阻力中黏压阻力占比较大,因此,优化过程中采用实尺度粘流直接计算不但可有效避免尺度效应,同时获得更准确的阻力及艉部伴流计算结果。
3)针对低速肥大船型的型线优化,降低艏艉压力梯度以减小黏压阻力,避免船身横波并减小散波波峰值以减小兴波阻力,此外,尽可能降低伴流目标函数值,获得较高的螺旋桨推进效率,从而提高船舶航行性能及营运经济性。
4)本文优化目标为静水阻力与伴流目标函数,可采用多目标优化算法进行多目标优化,建议进一步深入研究减小伴流目标函数对螺旋桨效率提升的比例,从而合理确定其权重因子,实现低速肥大船型的多目标优化。

