大口径透镜柔性支撑结构设计与分析

赵勇志，曹玉岩，韩西达，李玉霞

（中国科学院 长春光学精密机械与物理研究所，长春 130033）

对于大口径透镜（直径或长度大于300mm），传统刚性支撑因温度适应性差已无法满足要求，越来越多的大口径透镜采用基于quasi-kinematic原理的柔性支撑结构，如图1所示，具有支撑刚度高、温度适应性强、结构简单、无摩擦和滞后效应等优点。从经典三点柔性支撑结构出发，支撑结构可演化为多种形式，如图1（a）～（i）所示，其中（a）为詹姆斯韦伯望远镜中氟化锂透镜的柔性支撑结构[1]，（b）为Subaru望远镜近红外光谱仪UK-FMOS中透镜的柔性支撑结构[2]，（c）为MMT望远镜Binospec光谱仪透镜的柔性支撑结构[3]，（d）为火星红外光谱仪中椭圆分色镜的柔性支撑结构[4]，（e）为GOES-R中先进成像仪分光平面镜的柔性支撑结构[5]，（f）为韩国空间光学中心研制的bipod型支撑结构[6]，（g）为LMSSC公司空间近红外相机的六点柔性结构[7]，（h）和（i）为长春光机所研制的分别用于空间光学遥感器大口径主反射镜的Cartwheel型柔性支撑结构[8]和光刻物镜中透镜轴向支撑的多点柔性支撑结构[9-11]。尽管柔性支撑结构形式不同，但其本质特征与经典三点柔性支撑结构类似，即由多个柔性环节并联或串联而成，利用结构的柔度特性来适应环境温度变化引起的温度应力，利用结构的刚度特性来约束光学元件的位置。与金属材料相比，很多光学材料如氟化锂和硒化锌等虽具有优异的光学性能，但力学性能差且热胀系数高[12]，当温度变化范围较大时，将会发生较大的热变形，大口径透镜的变形将更为显著，这些热变形会给支撑结构设计带来巨大的挑战。

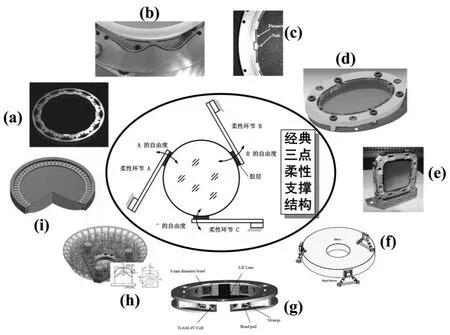
图1 典型柔性结构

透镜支撑结构设计目标包括[13]：（1）减小或消除可能造成镜面变形的局部应力；（2）补偿由支撑结构和镜体的不同热变形引起热应变或应力；（3）定位精度高，即在不同方位下因透镜重力引起刚体位移尽可能小。理想的支撑方式是含有三个正交轴的运动学支撑，能够约束镜体的三个位置和三个转动自由度[14]。然而，由于点接触会造成较大的局部应力，很难应用在实际支撑结构中。在实际中，通常采用含有有限接触面积的准运动学（Semi-kinematic）支撑方式，能够有效的分散局部应力。柔性结构以其重复精度高、无摩擦、加工制造容易且成本低等优点，作为一种准运动学支撑方式广泛应用于支撑结构中[15-17]。与传统柔性机构不同，透镜支撑结构中采用的柔性结构主要用于减小镜面变形且保持光轴位置，而并非产生线性或精密运动。

尽管柔性支撑结构具有以上优点，但其力学模型非常复杂，尤其是多个柔性单元同时作用。赵磊等[9]设计了光刻投影物镜透镜的轴向多点柔性支撑结构，将弹性片简化为悬臂梁模型，但对弹性片的数目与面形精度的关系未作深入分析。李宗轩等[8]针对空间遥感器大口径主反射镜提出了Cartwheel型双轴柔铰支撑结构，采用无量纲设计方法确定结构参数，尽管满足了设计要求，但无法确定此参数为最佳。Chin David等[13]和曹玉岩等[18，19]已对反射镜支撑结构的设计目标作了明确的描述，其要求是相互矛盾的，即将反射镜牢固的支撑在固定位置需要支撑应力来平衡反射镜重力，但支撑应力又将导致镜面变形。这两方面要求给支撑结构设计带来困难，尤其是柔性支撑结构的设计。

为解决上支撑结构设计问题，需根据使用要求对各个参数进行优化，进而得到合理的结构方案，而实现以上目的的关键是柔性支撑结构的力学模型。为此，本文针对一种圆弧形柔性支撑结构的建模方法进行了深入研究。

1 柔性支撑结构原理及简化

柔性支撑结构概念由 Yolder[20，21]提出，如图 1所示，由多个均匀分布的相同柔性单元构成。通常，透镜与支撑结构材料的热变形系数不一致，环境温度变化会引起不一致的结构变形或应力，进而影响镜面面形精度。柔性支撑结构在热变形方向上（径向）具有较大柔度，因此可有效减小由不一致的热变形引起的温度应力。此外，在其他方向上（如切向），具有较大刚度，能够保证支撑结构的定位精度。

如图1所示，为满足不同的需求，柔性支撑结构可设计为多种形式，本文仅研究如图2所示的圆弧形柔性支撑结构，所提出的分析方法可推广应用于其它类型柔性支撑结构的分析与设计。柔性支撑结构总体结构如图2（a）所示，主要包括外框架、柔性环节和透镜，透镜与柔性环节在连接点处粘接在一起，三维结构如图2（c）所示。

为研究图2（b）所示柔性环节在x-y平面内的力学特性，即面内刚度或柔度特性，对结构模型作如下简化：（1）与结构变形相比，透镜变形非常小可忽略，即结构中除柔性单元外其余部分视为刚体；（2）圆弧形柔性单元简化为两端固支的超静定曲梁，中点作用集中载荷。

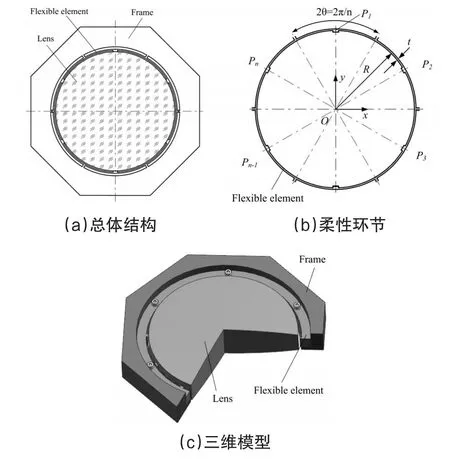
图2 透镜柔性支撑结构

2 力学建模

2.1 柔性单元建模

图2所示的柔性支撑结构，关键部分为对称分布的圆弧形柔性单元，其简化模型为如图3所示的超静定结构。由于透镜可视为刚体，且柔性支撑结构与透镜粘接在一起，因此在每个粘接点（Pi）处存在转动约束（Rotz=0）。图3所示柔性单元的力学特性由曲率半径R，厚度t，面外宽度b及中心角2θ决定，其中θ由切口数目确定。

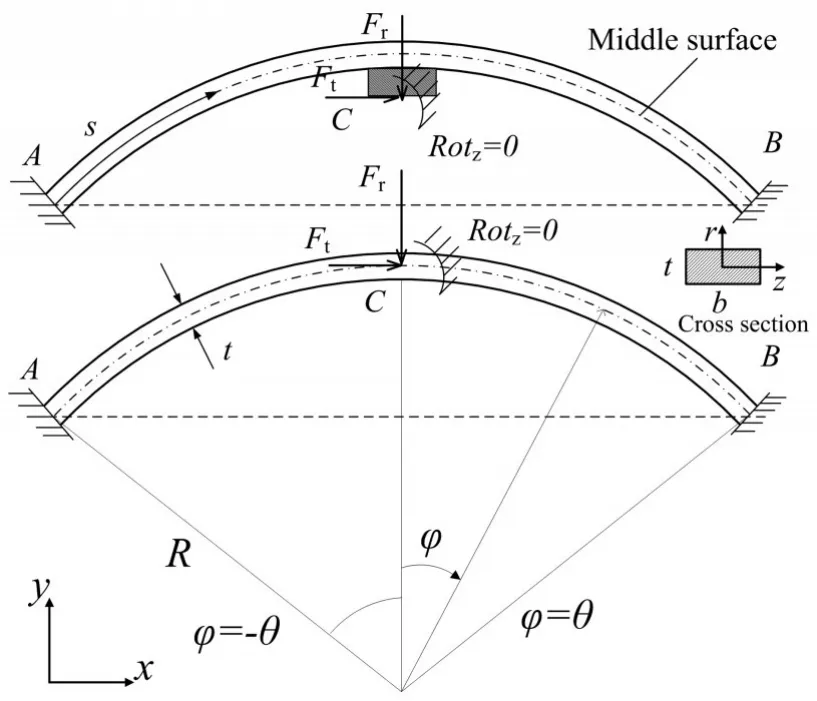
图3 柔性单元模型

柔性单元的面内（x-y）应变[22]为：

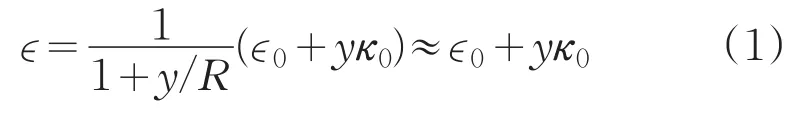
式中，y为厚度方向坐标。

中面应变ε0和曲率变化κ0分别为：

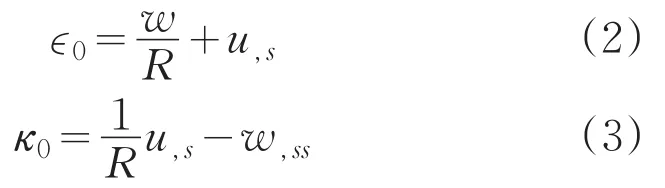
式中，u和w分别为中面切向和径向位移，s=Rφ为曲线坐标。

由（1）-（3）式并利用虚功原理[19]可得柔性单元的径向位移和切向位移分别为：

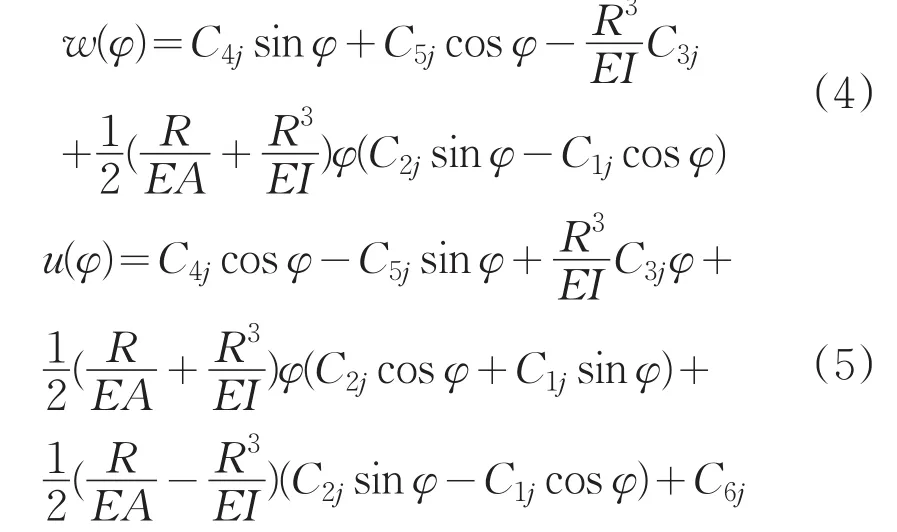
式中，Cij(i=1,2,…,6;j=1,2)为与集中载荷有关的常数。

令φ=0即可得到柔性单元的径向及切向刚度分别为：

由式（6）和式（7）可知，径向载荷仅引起柔性单元的径向位移，切向载荷仅引起切向位移。

2.2 结构整体建模

图2所示柔性环节的力和位移分析如图4所示，其中β为初始角度。图中Fi表示连接点Pi处的外力，可将其分解为径向力和切向力Fir和Fit，Fiy和Fix为Fi的竖向分力和水平分力，δir和δit表示连接点Pi处的径向位移和切向位移，δiy和δix表示竖向位移和水平位移，n为切口数目。

将Fiy和Fix用径向力和切向力Fir和Fit表达为

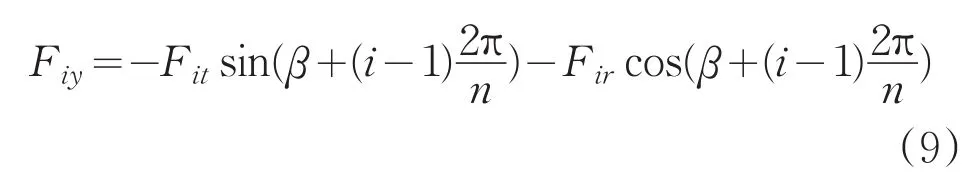
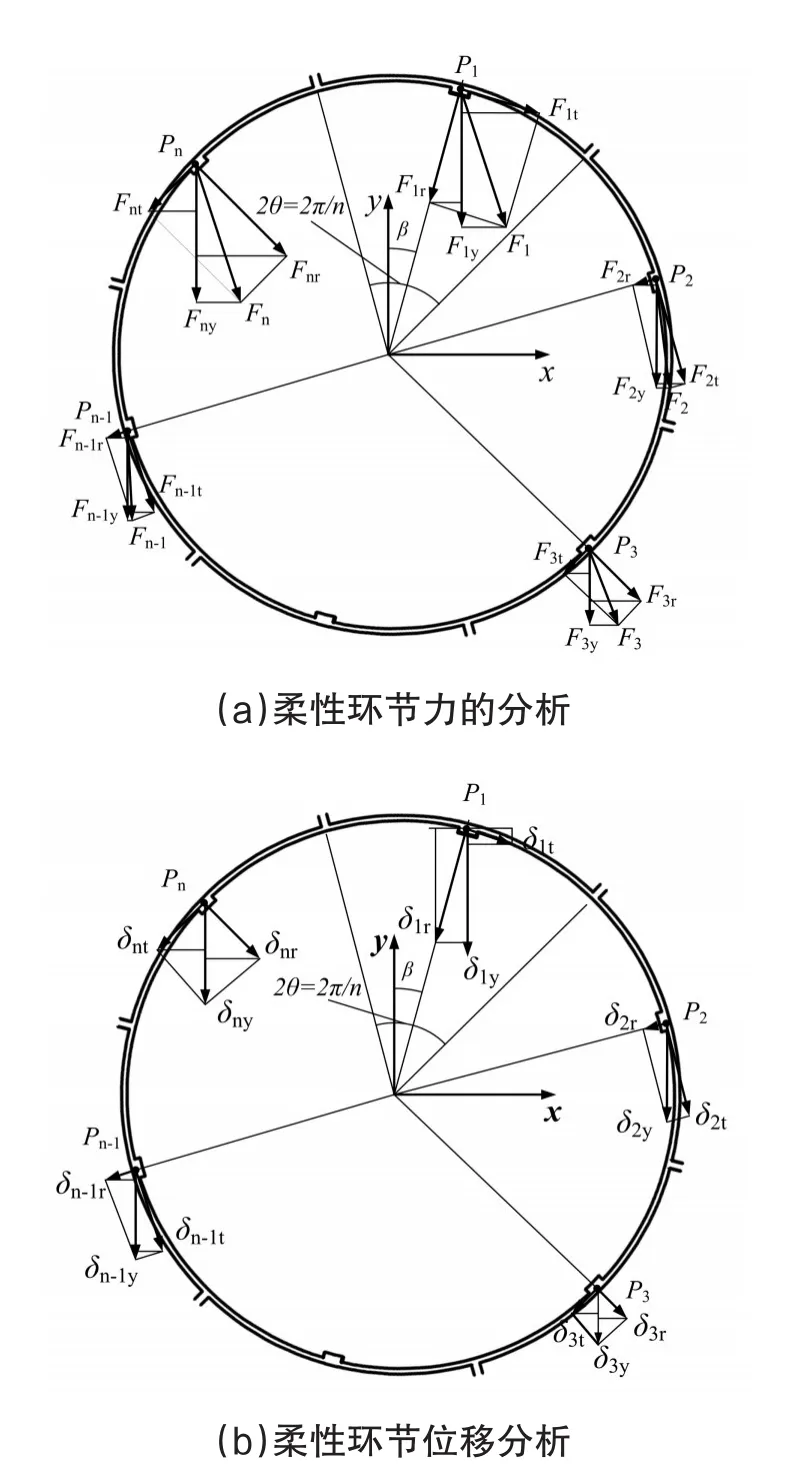
图4 柔性环节力与位移分析

若外力F施加在y轴方向，对各点分力求和可得：

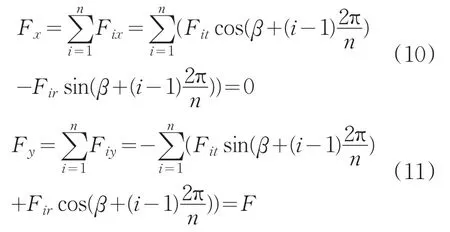
将δiy和δix用径向和切向位移δir和δit表示，且利用透镜刚体假设，即则各连接点Pi处的位移一致，则由式（8）-（11）可得：

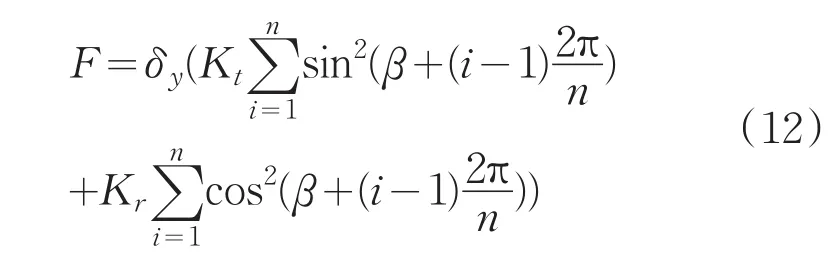
若n＞2，则求和表达式和与初始角β无关，且均等于n/2。柔性环节的刚度为：

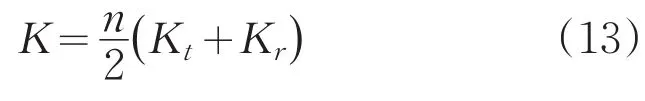
至此，推导出了柔性支撑结构的整体刚度表达式（13），为径向刚度和切向刚度的线性组合，与初始角度β无关。

3 数值仿真与实验

考虑如图2所示的透镜柔性支撑结构，支撑结构设计需要考虑多方面因素，如材料选择、工作环境、结构参数等。为了验证本文提出的圆弧形柔性支撑结构及推导的力学模型，进行了相应关仿真分析及实验验证，具体内容如下。

3.1 柔性支撑结构力学模型验证

为了本文推导的柔性支撑结构力学模型，建立如图5所示的实验测试装置，包括力传感器（load-cell）、位移平台、光栅位移传感器、PC计算机。位移传感器和力传感器测量的数据通过计算机串口（RS232）同时采集到计算机中。力传感器精度为0.01N，光栅位移传感器的精度为0.1μm。这里需要说明，本部分主要测试力学模型，而对包含透镜的支撑结构进行测试容易破坏透镜，因此本部分采用模拟结构进行测试，与实际支撑结构有所区别。

图5 柔性环节实验测试装置

对柔性支撑结构施加一个的作用力，测量施力点的位移，采用有限元软件对该过程进行线性和非线性仿真，然后比较理论、实验及仿真结果。实验件模型如图6所示，材料选择钛合金TC4，其材料参数如表4所示，实验件的几何参数如表1所示。

表1 几何参数

图6 环形柔性结构实验件

为了验证支撑结构整体力学模型，针对图6所示的圆弧形柔性结构，考虑到圆周方向上的对称性，测试方向如图7所示。对结构不同方向上的刚度进行实验测试及有限元仿真计算，结果如图8所示。

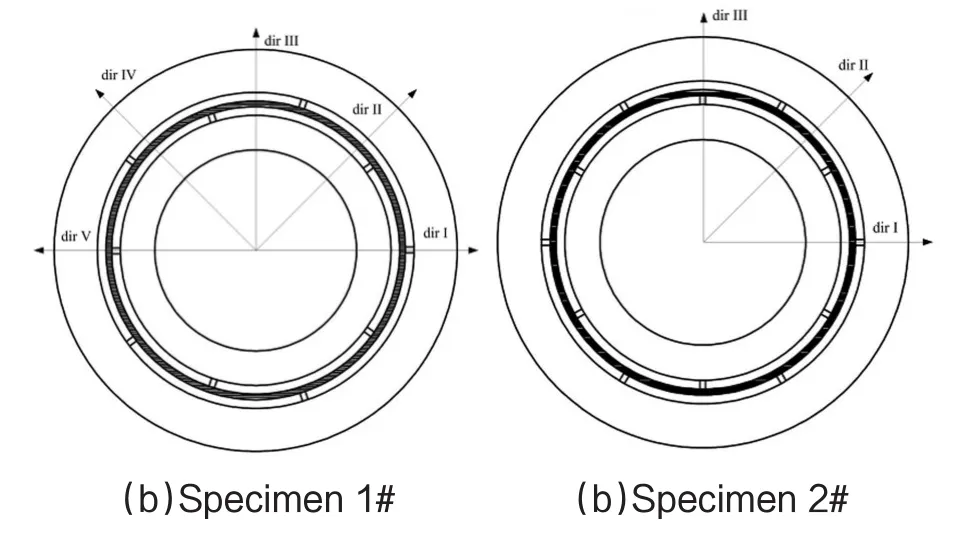
图7 环形柔性结构刚度测试方向

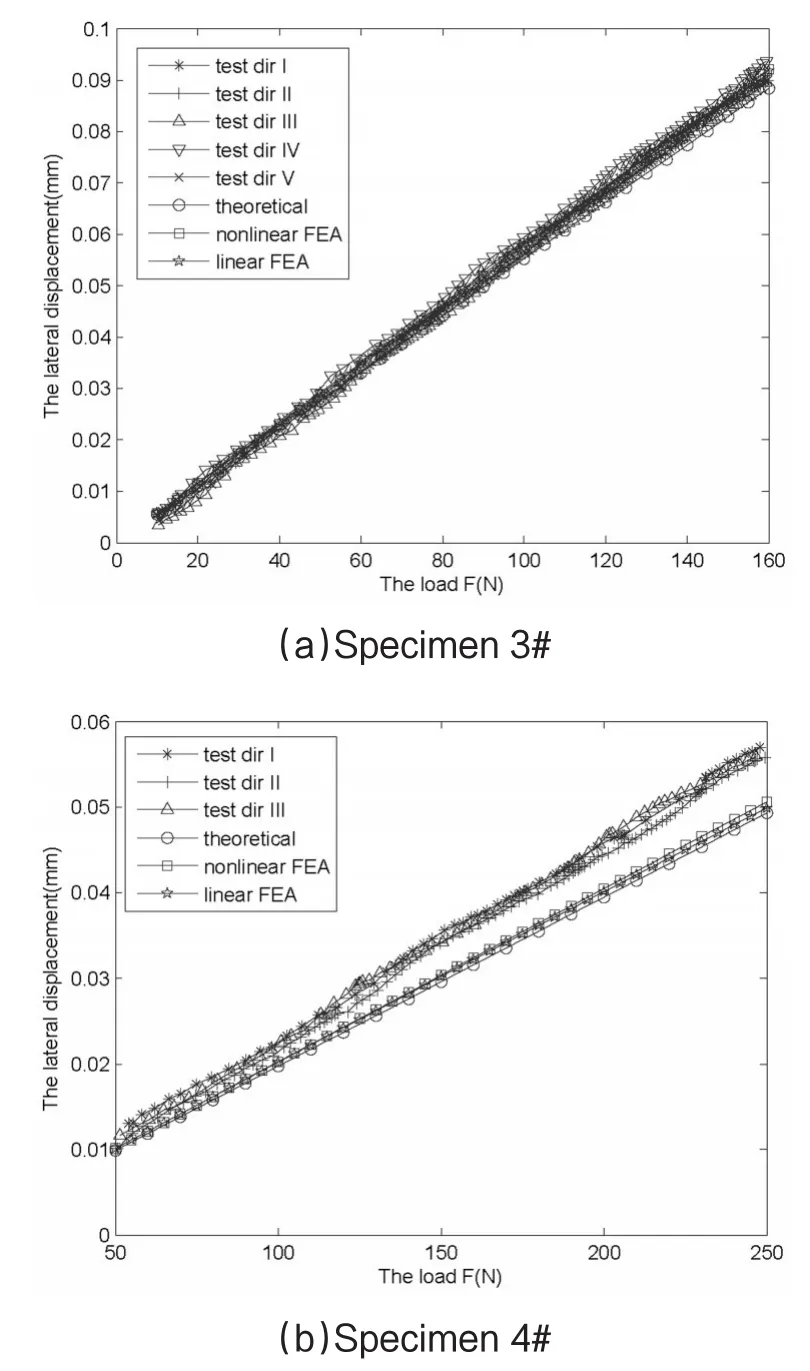
图8 环形柔性结构刚度测试与仿真结果

通过比较理论、仿真及实验结果可得出如下结论：（1）1#实验件理论、实验及有限元仿真结果吻合非常好。（2）4#实验件结果间存在一定的偏差，但理论与线性和非线性有限元仿真结果一致，表明了误差主要来源于加工。（3）在各个测试方向上，3#和4#实验件的实测位移数据基本一致，表明在各测试方向上具有相同的整体刚度，与理论分析一致。

3.2 支撑结构整体热变形仿真分析

透镜圆弧形柔性支撑结构如图2所示，各组成部分材料参数如表2所示。为了匹配透镜材料与结构材料之间热胀系数的差异性，在柔性支撑结构与透镜连接处增加了粘接垫，其材料为4J32，粘接垫的热胀系数可调节为与透镜材料一致，进而减少因热胀系数差异性引起的热应力，粘接垫与透镜及柔性环节之间通过环氧胶粘接。结构几何及材料参数如表3和表4所示。

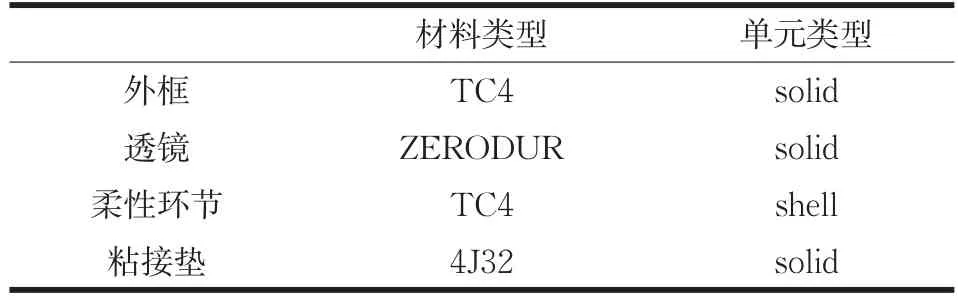
表2 材料及单元类型

表3 几何参数

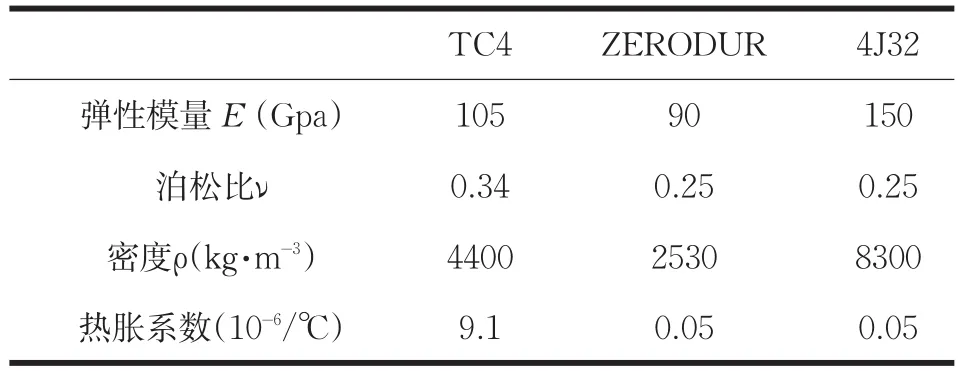
表4 材料参数

透镜柔性支撑结构设计的目标是尽可能提高透镜位置精度和面形精度。透镜位置偏差主要由柔性支撑结构的整体刚度及透镜重力决定，光轴水平时位置误差达到最大值。为了提高位置精度，柔性支撑结构要求具有较高的刚度。面形精度主要由柔性支撑结构中各个柔性单元径向支撑刚度决定，径向支撑刚度越大，相同热变形产生的热应力将会越大，进而导致面形误差越大。为了提高面形精度，柔性单元应具有较大的柔度。为解决上述相互矛盾的设计目标，需要根据使用要求，对各设计参数进行匹配，进而得到合理的方案。

柔性支撑结构参数设计包括确定柔性环节切口数目n、柔性片厚度t、面内宽度b。针对表3给出的透镜参数对不同设计参数进行仿真分析，透镜光轴位移及柔性环节径向刚度如图9和图10所示，其中图9所示曲线从下至上宽度b依次取值为6、8、10、12、14、16mm，图10所示曲面从下至上切口数目n依次取值为6、8、10、12。从图9中可以看出，透镜光轴位移随着柔性片厚度t、宽度b及切口数目n的增大而减小，厚度t对位移的影响显著，在t≥0.4mm且n≥8时，光轴位移均小于0.05mm（位置公差要求）。此外，由图10可以看出，随着柔性片厚度t、宽度b及切口数目n的增大，径向支撑刚度Kr增大，而径向支撑刚度会直接影响透镜面形精度，因此径向支撑结构不宜过大。综合以上两方面因素，柔性支撑结构宽度应尽可能大，厚度t应尽可能薄，最终确定柔性支撑结构切口数目为8，宽度b为16mm。

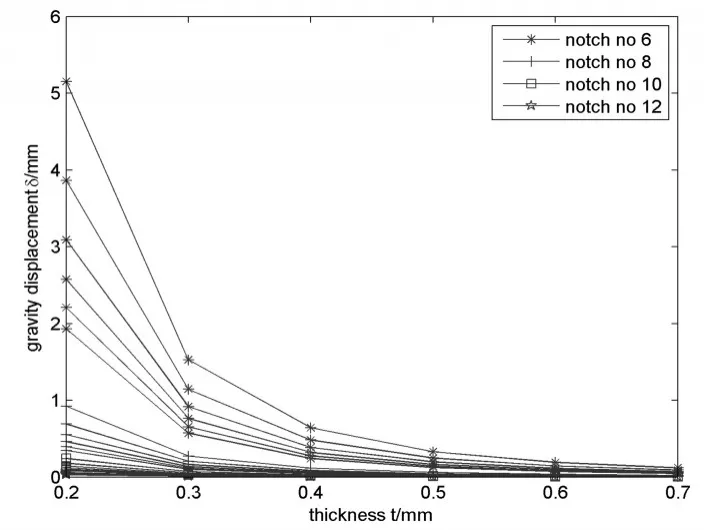
图9 透镜光轴位移变化

图10 柔性单元径向刚度

为了验证柔性支撑结构的温度适应性，对8切口圆弧形柔性支撑结构，按表2-表4所示参数建立结构有限元模型如图11所示，环境温度-40℃～+40℃，柔性片厚度为0.2mm～0.5mm情况下，分析透镜柔性支撑结构整体性能。透镜的面形RMS和镜面PV值如图12和图13所示。

图11 支撑结构有限元模型

图12 镜面RMS值

从图12和图13中可以看出，由于支撑结构与透镜材料热胀系数存在偏差，环境温度变化时镜面与支撑结构间会产生热应力进而影响镜面面形精度。在除20℃外的任意温度下，随着径向刚度的增大，镜面RMS值和PV值随之变大。综合比较透镜的位置精度及面形精度，即图9和图12，可发现柔性片厚度为0.4mm情况下透镜的面形精度及光轴位移均比较理想，因此最终设计参数确定为：n=8，b=16mm，t=0.4mm。环境温度-40℃条件下，透镜的应力分布如图14所示，从图中可看出，温度应力主要集中在柔性环节与透镜的粘接区域，表明柔性支撑结构能够有效缓解透镜与支撑结构间的热应力，使透镜的温度应力均集中在连接点附近的小区域内，进而改善透镜面形精度。

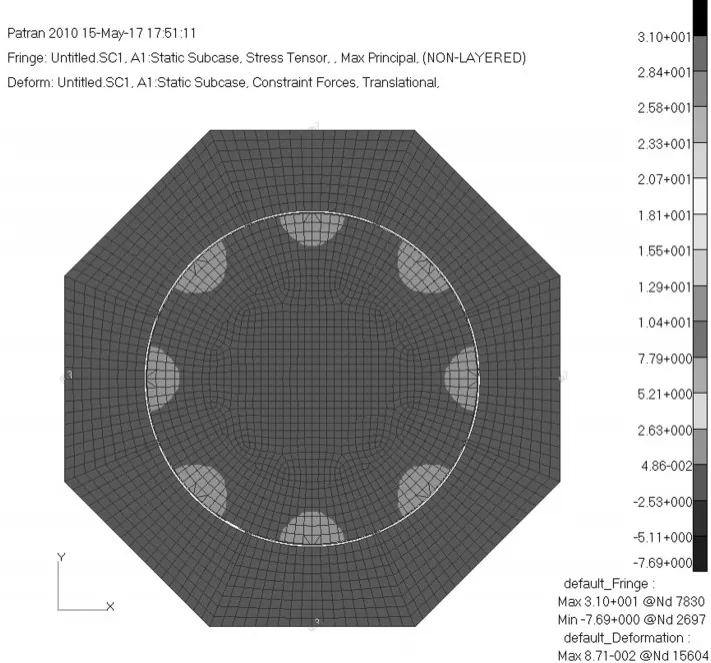
图14 透镜的应力分布

4 结论

本文针对光学元件支撑结构中广泛采用的圆弧形柔性结构进行了理论分析，并进行了有限元仿真及实验。首先，圆弧形柔性支撑结构由圆周对称分布的柔性单元组成，将柔性单元简化为超静定圆弧梁，推导了柔性单元的径向及切向刚度。然后，假设透镜为刚体，根据力平衡条件及变形协调条件，推导了环形柔性结构的整体刚度。最后，对推导的力学模型进行了有限元仿真和实验验证。

有限元仿真及实验测试结果表明：推导圆弧形柔性支撑结构整体刚度与有限元及实验测试结果相吻合，误差小于3%，表明本文推导的理论模型能够用于柔性支撑结构的设计与分析。此外，通过对300mm透镜仿真分析，表明柔性支撑结构能够有效的降低透镜与支撑结构间的温度应力，进而提高支撑性能。