射流冷却玻璃钢化过程均匀性的数值研究

朱 璐，顾平道，王如歌，严心榕，李 静

(东华大学环境科学与工程学院，上海 201620)

水平玻璃钢化法是当前世界上使用最普遍的一种玻璃钢化方法，它是通过辊道传送玻璃，将玻璃传送到加热炉内加热，然后将玻璃传送到冷却炉快速冷却得到钢化玻璃[1]。淬冷是水平玻璃钢化的关键工艺，钢化玻璃的质量很大程度上是依赖于风嘴对玻璃表面的阵列射流吹风冲击传热。这种将流体通过圆形或狭缝形风嘴直接喷射到固体表面进行冷却或加热的方法称为冲击射流换热，这是一种极其有效的强化传热方式，由于流体直接冲击固体表面，流程短而边界层很薄，因此得到了广泛的应用[2,3]。

玻璃淬冷是一个包含空气和玻璃的温度场、应力场的复杂耦合过程，而其中风嘴的大小、间距、阵列方式与吹风均匀性等因素对钢化玻璃的质量有着至关重要的影响[4]。尽管针对冲击射流冷却国内外学者已经开展了大量研究，但针对玻璃钢化冷却吹风过程的射流冲击冷却过程的研究却极为少见。该文通过数值模拟的方法建立风嘴射流冷却玻璃的几何模型，探究不同个数的风嘴排列射流吹风冷却4 mm薄玻璃过程中的流场分布情况，用局部努赛尔系数(Nu)来表征射流冷却玻璃表面的冷却效果，为实现更均匀地射流吹风冷却玻璃表面提供参考依据。

1 模型建立与数值模拟

1.1 数学模型的建立

该文研究的是空气射流冷却从加热炉出来的高温玻璃(约600 ℃)，所研究的流体为空气，在Fluent中流体材料选取air。整个冷却过程是一个基本稳定的过程，故采用稳态求解器来进行求解。其基本控制方程如下:

连续性方程

(1)

动量方程

(2)

(3)

(4)

能量方程

(5)

用局部努塞尔系数Nu来表征射流吹风冷却效果，其计算方程式为

(7)

式(1)～式(7)中,ux、uy、uz分别为x、y、z3个方向的速度分量，m/s；t为时间；s；ρ为密度，kg/m3；p为流体微元体上的压强，Pa；fx、fy、fz为3个方向的单位质量力，m/s2，质量力只受重力，且y轴垂直向上，故fx=fz=0，fy=-g；γ为流体的运动粘度，m2/s；C为比热容；T为热力学温度，K；λ为流体的导热系数。d表示喷孔直径，m；h表示被射流冲击表面的局部传热系数，w/(m2·k)；λ为空气介质的导热系数，w/(m·K)。

1.2 物理模型的建立

在冷却工艺过程中,钢化炉的风压参数、施加在玻璃表面的风压和风栅与玻璃的间距之间存在着相互对应的关系，太大或太小都会使生产出来的玻璃带有缺陷。在加工4 mm薄玻璃时，吹风风压为8 000 Pa，风栅与玻璃上表面的间距为10 mm，玻璃表面的温度为873.15 K。为了简化模型，进行以下假设：

1)喷射介质不可压缩，为常物性；

2)射流离开喷嘴时的速度均匀；

3)被冲击表面为光滑的玻璃表面。

图1所示为圆形单孔冲击玻璃表面示意图，玻璃板和喷孔板的长宽均为L=100 mm，W=100 mm，射流圆孔的直径D=5 mm，喷孔板和玻璃板表面距离为H=10 mm。对于多孔射流将进行等距排列建立几何模型，喷嘴的数量不同则射流孔中心距Cn与孔径D之比也不同。该文定义对于多孔射流，孔间距Cn中的n表示喷嘴个数，该文通过改变喷嘴个数得到4种多孔射流物理模型，其几何参数如表1所示。

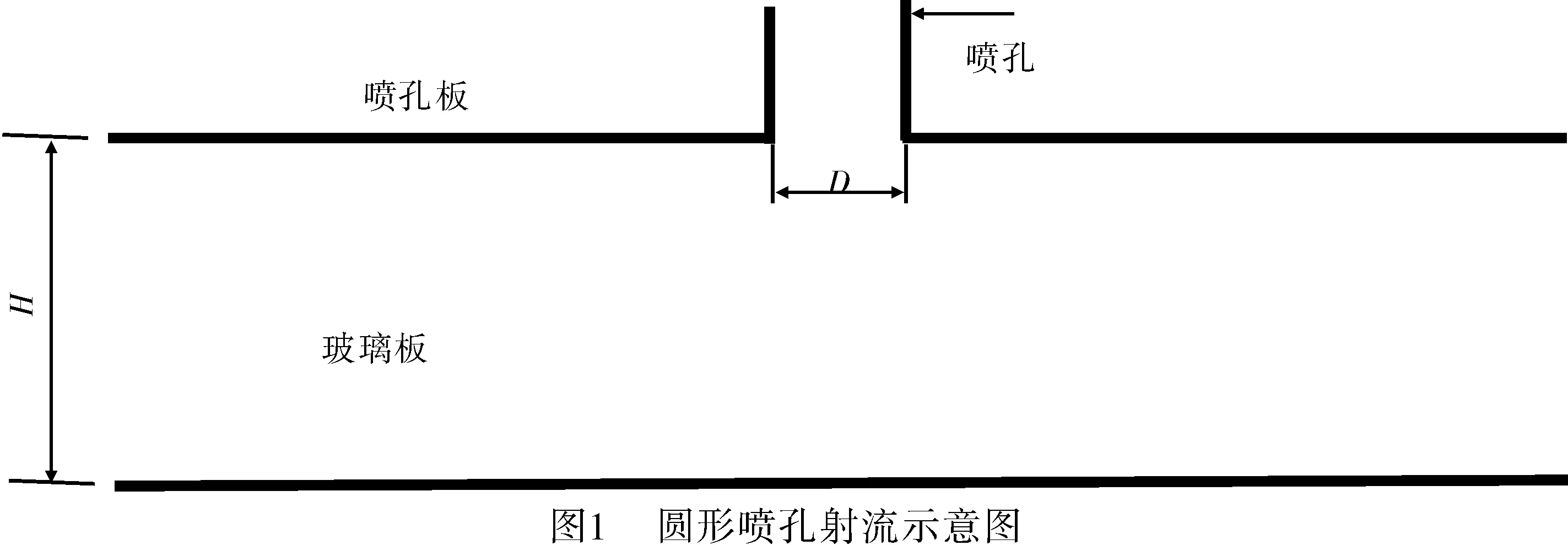
表1 4种多孔物理模型的几何参数

参数喷嘴个数n喷嘴孔间距Cn孔间距比Cn/DC33336.6C55204.0C77142.8C99112.2

1.3 边界条件

1)喷嘴出口：速度入口，温度为常温；

2)冲击壁面：玻璃板区域为无滑移壁面，初温为873.15 K；

3)喷孔板平面：绝缘，无滑移壁面；

4)出口：压力出口，常压。

1.4 求解方法的确定

利用Fluent计算流体力学软件，以不可压缩流体流动基本原理和流热固耦合有限体积法为基础，通过求解冲击射流控制方程组以获得从钢化加热炉出来的高温玻璃表面的流场分布及换热情况，对其冷却情况进行数值模拟。模拟的过程选择Relizablek-ε双方程模型，壁面采用非平衡壁面函数，选择Simple算法来求解压力-速度耦合，压力插补格式采用二阶格式，采用二阶迎风格式算法离散动量项，采用一阶迎风格式算法离散湍动能和湍流耗散速率项，收敛的标准是判断相对残差是否小于10-5。

2 网格无关性和实验验证

2.1 网格无关性验证

使用Gambit软件，采用六面体网格对模型的计算区域进行网格划分，为保证网格数的合理性，使用Relizablek-ε湍流模型对计算中的网格进行网格无关性验证。下面对全部八种模型进行网格无关性验证，模型一为后续实验验证所需模型，验证的实验来自文献[2]，模型为圆管(D=6 mm，l=40 mm)射流冷却高温304不锈钢，尺寸为300×300×10 mm；模型二为单孔射流冷却高温玻璃，模型三～模型六为表1中的4种多孔射流冷却模型。图2为不同网格数量时的网格无关性验证，以平均对流换热系数作为衡量指标。通过该图可以看出，模型一在网格数量小于160万时，冲击表面的平均对流换热系数随着网格数量的增加而增大，当网格数量大于160万后，平均对流换热系数随网格数量的增加几乎不变；其余7个模型的网格数量都是在网格数小于110万时，冲击表面的平均对流换热系数随着网格数量的增加而增大，当网格数量大于110万后，平均对流换热系数随网格数量的增加几乎不变。因此本文在模拟模型一时取网格数量为160万时进行模拟，其余七个模型则选取110万的网格进行模拟。

2.2 实验验证

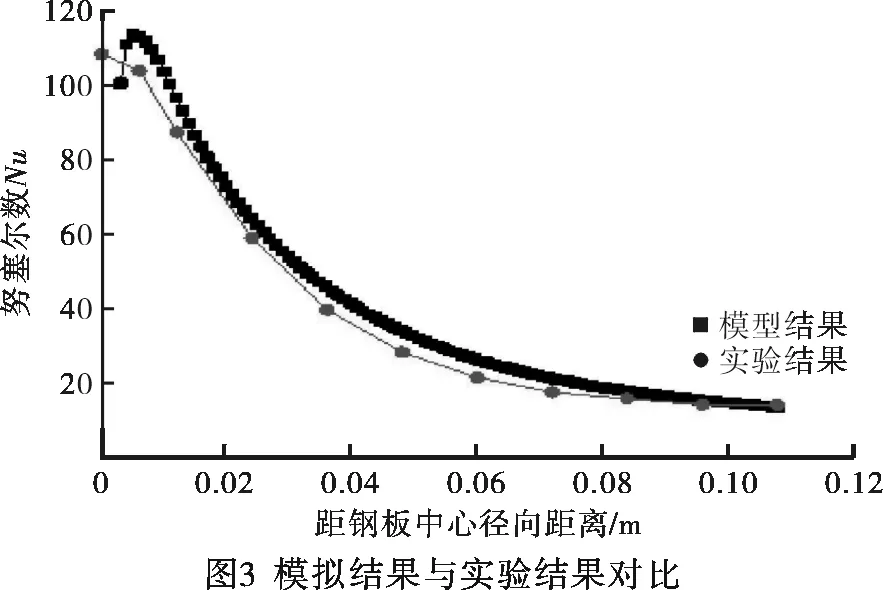
为验证模拟过程的有效性和可靠性，将现阶段已得到的实验方法做模拟，已验证该文采用的数值模拟方法的可靠性。实验验证的对象是单圆孔气体射流冷却高温钢板[5，6]，钢板表面温度为1 048.15 K，喷嘴进口流量为8.5 m3/h。选用二阶迎风的离散格式以提高计算精度，并采用Simple算法与Relizablek-ε模型，数值模拟结果与试验结果一致，见图3。

3 数值模拟结果与分析

3.1 单孔冲击玻璃表面的传热特性分析

图4为单孔射流冷却玻璃时的速度分布云图,图5为玻璃表面径向的对流换热系数与局部努塞尔数分布。从图4中可以看出，空气从喷嘴垂直入射冲击时，会与周围静止的介质之间发生动量交换，使射流的直径增大。冲击到玻璃表面时，速度的方向会发生改变，向四周的出口流出，而速度的大小也逐渐减小，但在垂直于喷嘴中心的部分区域会形成驻点区域，出现“凹坑”现象，而在“凹坑”附近的区域的速度较大，随着区域的增大速度也逐渐减小。从图5中可以看出，对流换热系数和努塞尔数沿径向出现两个峰值，第一个峰值出现的原因是在射流冲击玻璃表面时，在驻点区域形成很薄的速度边界层和热边界层，因此换热强度较大。第二个峰值出现在半径略大于喷嘴半径的位置，这是因为在这个区域的速度在冲击力的作用下导致速度增大且形成了回流，从而增强了换热能力。

3.2 多孔冲击玻璃表面的传热特性分析

对于单孔射流的换热特性已经有过很多实验和模拟研究，但是对于多孔射流的研究却极少，而研究多孔的射流特性对实际射流冲击及射流均匀性具有很重要的意义。图6所示为模型3～6(喷孔个数分别为3、5、7和9)的玻璃表面离中心点径向努塞尔数的分布曲线图。

每一个模型的中心射流孔都位于玻璃中心的正上方，即图中的原点位置。通过努塞尔数分布图可以看出，射流驻点位置即“凹坑”中心的努塞尔数最小，换热情况最差，“凹坑”边缘的努塞尔数最大，换热效果最佳，而在两孔之间的中心位置由于发生碰撞形成上喷流，增强换热。射流孔的个数和间距对每个射流孔冲击到玻璃表面的“凹坑”中心区域换热的影响可以忽略，但是对“凹坑”边缘及周围区域的影响较大。随着射流孔个数的增多，射流孔中心间距的减小，“凹坑”边缘及附近的努塞尔数也增大，换热效果变强，这是因为在孔之间的区域射流会互相影响，发生碰撞，从而增强玻璃表面的换热。从图6中可以看出，当喷孔个数为三时出现了努赛尔数的最小值，九喷孔次之，五喷孔和七喷孔的最小值相差不大。而当喷孔个数为三或五时，努赛尔数的最大值相差不大，当喷孔个数大于五之后，玻璃表面的努赛尔数随着喷孔个数的增多而增大。产生上述差别的原因是当喷孔个数为三时，喷孔的间距较大，中心部分的气流速度小，导致换热效果差，因此温度较高，努赛尔数较小。随着喷孔个数的增多，这种情况得到改善，但当喷孔个数大于五后，喷孔之间的间距越小，彼此之间的气流影响越大，导致喷孔之间区域的空气横向流动增强，换热效果增强，努赛尔数增大，而驻点区域的最小努赛尔数变化不大，所以换热均匀性变差。

(8)

(9)

(10)

不同模型的努赛尔数变异系数见表2，通过表格中的数据可以看出当喷孔个数为五(即前文中的模型四)，喷孔的中心间距为20 mm时，空气射流冷却玻璃表面时的换热均匀性最佳。

表2 不同喷孔数的努赛尔数变异系数

4 结 论

该文运用Fluent模拟软件对玻璃钢化的射流冷却过程进行了三维仿真研究。通过改变射流风嘴的间距的设计，对冲击冷却效果和射流到玻璃表面的均匀性进行了分析。

a.单孔射流冷却时，在玻璃表面会形成“凹坑”现象，在“凹坑”中心的速度接近0，边缘区域的速度最大，向四周逐渐减小。

b.多孔射流时，在一定范围内，随着孔数量的增加，孔间距的减小，对“凹坑”中心的努塞尔数影响可以忽略，但两孔中间区域的努塞尔数呈增大的趋势，有利于玻璃表面的换热。而超过一定范围后，努塞尔数会随间距的减小而减小，不利于换热。

c.多孔射流的最佳风嘴中心间距为20 mm，此时玻璃表面的努塞尔数分布最均匀，最有利于玻璃钢化过程中的均匀冷却。