基于CarSim仿真的公路车道数变化段指标研究

潘兵宏，赵悦彤，霍永富



基于CarSim仿真的公路车道数变化段指标研究

潘兵宏1,2，赵悦彤1，霍永富1

(1. 长安大学 公路学院，陕西 西安 710064； 2. 长安大学 特殊地区公路工程教育部重点试验室，陕西 西安 710064)

针对公路车道数变化处过渡段的长度或渐变率设计指标的取值对于安全行车具有重要影响，通过分析公路车道数变化处过渡段车辆行驶需要换道特点，提出一次函数修正型正弦曲线换道模型，并建立基于车辆换道轨迹的车道数变化处过渡段渐变率计算模型。通过换道轨迹模型中特征参数的分析，确定不同设计速度与超高横坡情况下车辆换道的横移宽度与纵向移动距离，进而提出车道数增加或减少一个时，过渡段的长度和渐变率推荐值。研究结果表明：车道数变化过渡段的长度和渐变率不仅与设计速度相关，且与超高横坡有关。提出的过渡段长度和渐变率的建议值可为今后公路车道数变化过渡段的设计提供参考。

车道数变化段；过渡段；渐变率；换道模型；正弦曲线；超高横坡

当公路横断面车道数发生变化时，在变化处需设置过渡段，过渡段的渐变率的大小不仅影响路容美观和工程造价，而且对安全行车有重要影响[1]。车道数变化过渡段是前后宽度变化的衔接部分，对于驾驶人员而言，驶入该区域后需要接受处理的信息量突增，如若不能妥善操作，会引发交通事故。所以车道数变化过渡段的长度或渐变率应该满足驾驶员以设计速度行驶，并能安全变换车道。然而，国内外对过渡段的设计指标研究较少。在公路设计中，一般是从线形连续方面来保障其顺适过渡,《公路工程技术标准》[2](JTG B01—2014)(以下简称《技术标准》)仅强调不同道路等级与设计速度下宽度衔接应协调。《公路路线设计规范》(JTG D20—2006)[3](以下简称《路线规范》)中没有对车道数变化路段的渐变率或过渡段长度进行规定与说明。道路交通标志和标线》(GB5768—2009)[4](以下简称《标志标线》)中给出了较为详细的渐变段计算方法和取值规定，但其计算模型中没有考虑驾驶员特性、道路几何线形和超高等的影响。金珊珊[5]采用圆形和缓和曲线换道轨迹模型，从几何特性方面对宽度过渡段的指标进行了研究，研究中没有考虑横向加速度和横向加速度变化率的要求，且采用的轨迹模型中曲率不连续。因此，有必要对车道数变化过渡段的设计指标(包括长度和渐变率)进行研究，为设计人员提供参考，降低宽度过渡段发生事故风险。本文将重点探讨公路车道数变化处过渡段的长度和渐变率两个指标。车道数变化路段主要包含：爬坡车道、辅助车道及公路横断面车道数增加或减少的路 段[6]。在此类过渡路段内车辆一定伴随有车辆换道的现象，而车辆能否安全舒适的换道是宽度过渡段合理性的直观体现。因此，首先分析研究车辆行驶轨迹，选择合适的换道模型，再研究过渡段渐变率模型，最后提出车道数变化过渡段的长度和渐变率指标建议值。

1 车辆换道轨迹模型

通过分析国内外关于宽度变化设计指标的研究成果，结合车道数变化处的车辆行驶特性可知，宜采用换道模型来分析车道数过渡段的长度和渐变率指标。目前，国内外常用的换道模型有以下4种：第1种是一次函数模型[7]，但该模型存在起、终点处曲率不连续，且换道过程中曲率不变化，实际行车中不可能实现的缺点；第2种是圆直模 型[5, 8]，认为换道轨迹由两段反向圆曲线组成，该模型存在曲率变化不连续，且起、终点曲率不为0的问题；第3种是缓和曲线模型[5, 8]，该模型认为换道轨迹由两段两端曲率为0的缓和曲线组成，因此该模型存在轨迹中点处曲率反向突变的问题；第4种是正弦曲线模型[8,10]，该模型曲率变化均匀，线形连续，是目前常用的换道计算模型，但其存在曲率最大值出现在换道的起终点，与实际行车特点不符的缺点。根据杨建国等[9]的研究成果可知实际换道过程中应满足2条基本原则：1) 换道过程中，行车轨迹的曲率应连续变化，不会发生突变；2) 换道轨迹起、终点的曲率最小为0。因此上述4种模型均存在不足，不宜直接使用。

实际行车时，除了个别激进型驾驶人外，一般驾驶人会连续均匀打方向，确保车辆行驶安全稳定换道，因此，车辆轨迹线的曲率应连续变化。针对上述模型的不足，本文综合一次函数换道模型和正弦曲线换道模型的优点，提出一次函数修正型正弦曲线换道模型。而一次函数修正型正弦曲线换道模型有2个突出优点：一是此模型基础函数属于正弦函数，曲线上各个点的曲率连续变化，无曲率突变点，与大多数驾驶员操作车辆的行为相吻合；二是此模型起终点曲率为0，与实际换道的情况更符合，车辆换道轨迹如图1所示。

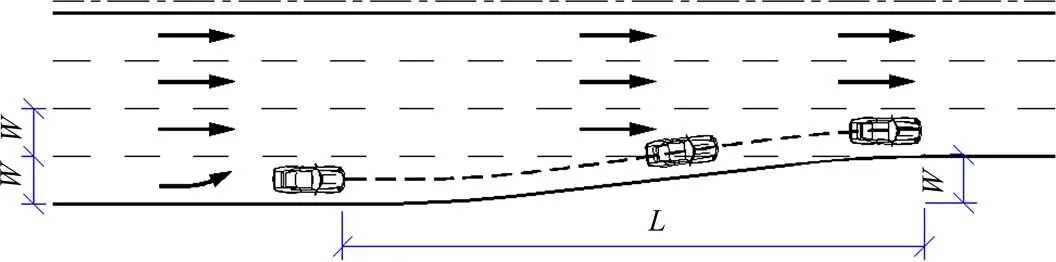
图1 一次函数修正型正弦曲线换道模型运行轨迹图

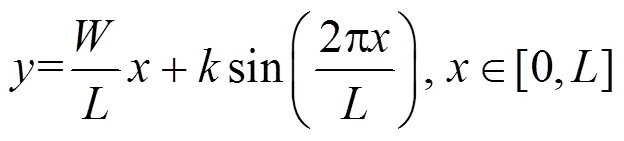
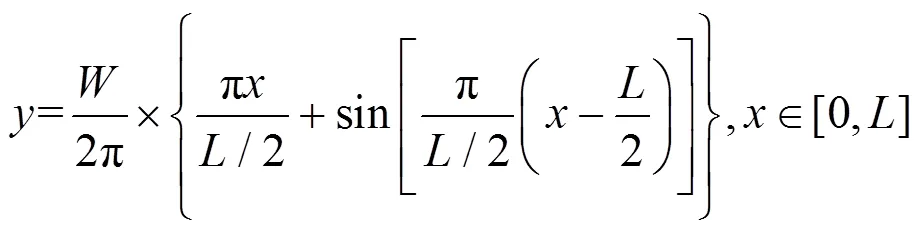
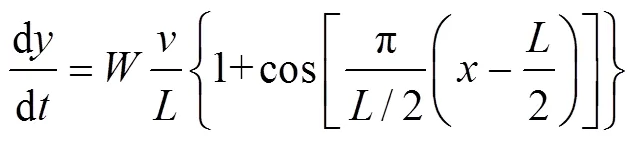
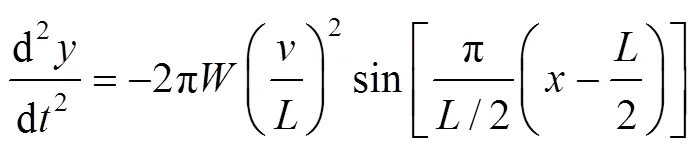
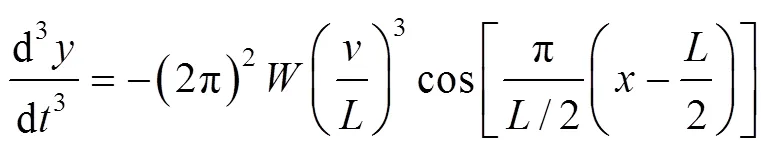
其中：max为最大允许横向加速度，m/s2；max为最大允许横向加速度变化率，m/s2。

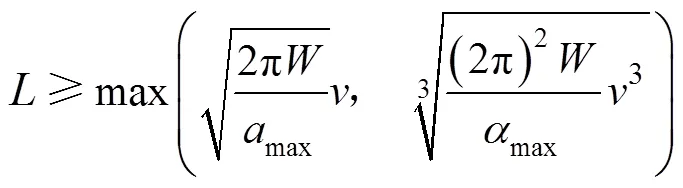
若确定了车辆完成换道横向移动的距离、最大允许横向加速度max及最大允许横向加速度变化率max则可以根据式(8)计算不同速度下的过渡段最小长度，因此，下面分析式(8)相关参数的取值。

2 过渡段指标值的确定

2.1 换道横移距离

一次换道横移距离等于一个车道宽度。车道宽度规定仅与设计速度有关，《路线规范》中规定了公路不同设计速度下的车道宽度取值(表1)。

表1 公路单车道宽度

2.2 换道过程中最大允许横向加速度取值

车辆在换道时的离心力，用式(9)计算：

式中：为离心力，N；为汽车运行过程中的横向加速度，m/s2

因为路面超高很小，所以车辆的横向力满足式(10)：

式中：加速度=9.8 m/s2；为车辆的总重量，N；i为路面超高横坡。而横向力与车辆的总重量的比值为横向力系数，可以得到横向力系数与路面超高横坡和横向加速的关系式(11)：

用式(11)计算车辆换道时最大横向加速度的前提是能确定不同设计速度下的最大横向力系数。从驾驶的安全性与经济性来考虑，计算转弯半径时不宜大于0.17。《技术标准》规定了圆曲线为极限最小半径时的取值，但当车辆以设计速度行驶时，为保证驾乘人员有充分的舒适感，横向力系数的最大值取为0.05~0.06，结合车辆不发生横向滑移的要求与研究成果，可计算出不同速度下车辆安全(极限值)和舒适(一般值)换道时最大横向力系数(表2)。

在车道数变化路段，车辆换道包含左侧换道与右侧换道。2种换道受力方式不一样，需克服不同类型的超高影响。在左侧换道过程中，汽车首先需要克服当前车道的反向超高影响，在进入目标变换车道后便变为正常超高，右侧换道则相反。根据表2中的横向力系数取值，选择最不利情况下反超高路段作为控制因素，则用式(11)可算出不同设计速度与超高下车辆安全换道时最大允许横向加速度(表3)。

表2 安全换道时最大允许横向力系数

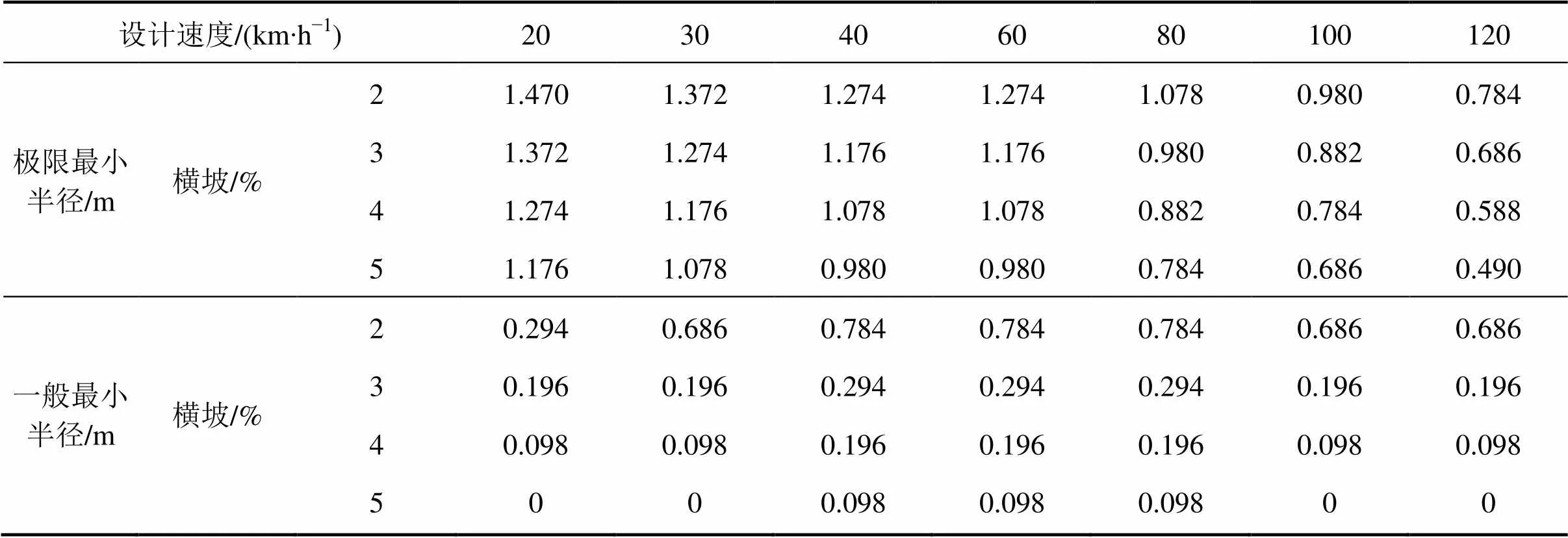
表3 最大允许横向加速度

2.3 换道过程中最大横向加速度变化率取值

横向加速度变化率是道路平、纵、横综合作用结果，其大小对行车舒适性影响很大。铁路上一般采用0.16~0.3 m/s3 [11]。公路上因车辆尺寸较小，行驶更灵活，可采用较大的数值，美国高速公路一般采用0.61 m/s3，考虑超高的影响，修正后采用0.305 m/s3；日本规定为0.5~0.75 m/s3[12]。杨少伟等采用0.5~0.6 m/s3[13]。此外，大量研究表明：人体能承受的最大横向加速度变化率在0.4~1.0 m/s3[14]，本文主要考虑驾驶人的舒适性和安全性，当车辆处于极限最小半径时，应保证安全性，适当放弃舒适性的要求，即：最大横向加速度变化率取1 m/s3；而车辆处于一般最小半径时，应当保证驾驶人的舒适性，即：最大横向加速度变化率取0.4 m/s3。

3 车道数变化过渡段渐变率研究

车辆换道横向移动宽度与纵向移动距离的比值即是车道数变化过渡段的渐变率，采用式(12)计算。

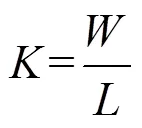
式中：采用式(8)计算。根据式(8)和(12)，可计算出不同设计速度下，车道数增加或减少一个时，过渡段的长度和渐变率如表4和表5所示。

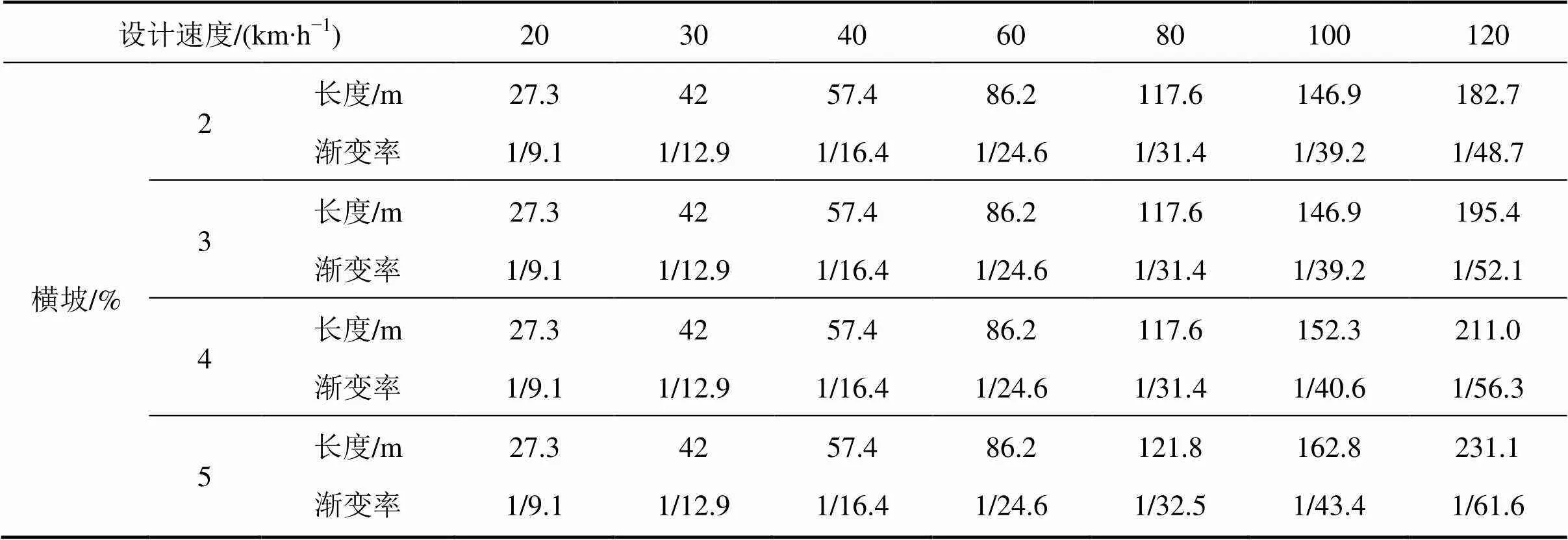
表4 车道变化过渡段极限最小长度(m)及渐变率

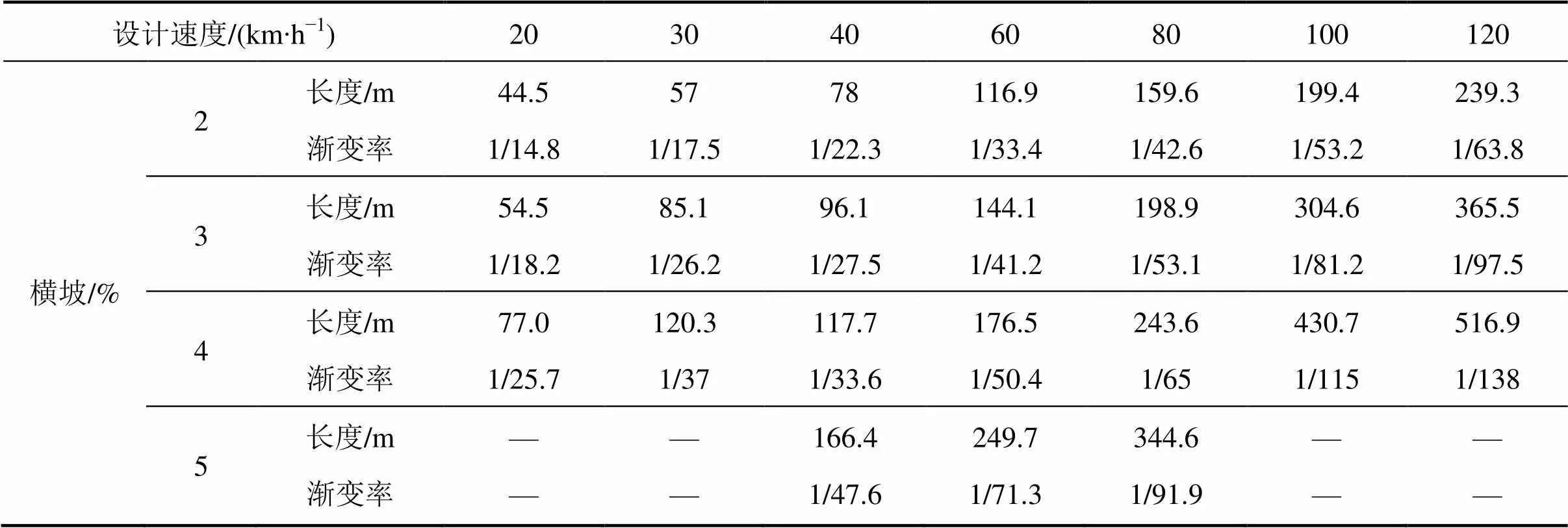
表5 车道变化过渡段一般最小长度(m)及渐变率

由表4和表5，可发现在路面超高横坡i相同时，设计速度越高，换道纵向移动距离越大，渐变率越小；设计速度不变，路面超高横坡i越大，换道纵向移动距离越大，渐变率越小，但超高对渐变率影响相对较小。所以，车道数变化段渐变渐变率的影响因素包含有设计速度、车道宽度和超高。从结果中还可以发现，曲线半径为极限最小半径，运行速度小于80 km/h，超高对于换道车辆的影响较小，大于或等于80 km/h时，超高对于换道车辆的影响较大，随着路面超高横坡的增大，换道所需的纵向移动距离也相应变大，渐变率变小。因此在在公路车道变化处过渡段长度或渐变率取值时，应注意2点：1) 尽量取一般最小长度对应的渐变率，如果条件受限，至少要满足极限最小长度对应的渐变率，这样才能保证驾驶人安全从容换道；2) 对运行速度小于或等于60 km/h的公路，可不考虑超高的影响；对于运行速度大于60 km/h的公路，过渡段的长度或渐变率必须要考虑路面超高横坡的影响，且车道变化过渡段宜设置在直线路段，或设置在路面超高横坡小于或等于3%的曲线路段。

因此当车辆变化一个车道时，建议一般情况下过渡段的长度和渐变率按表6中的一般值选用(表6中长度是取为整5 m后的结果)，特殊受限路段采用极限值。

《标志标线》中给出了车道变化处过渡段长度规定值，如表7所示。

对比分析表6和表7可以看出《标志标线》中给出的规范值比直线路段、一般路段及极限路段等的过渡段长度均小，并且规范中速度大于80 km/h的过渡段长度最小值为100 km/h不变，与实际情况不符，本文给出的建议值较全面。

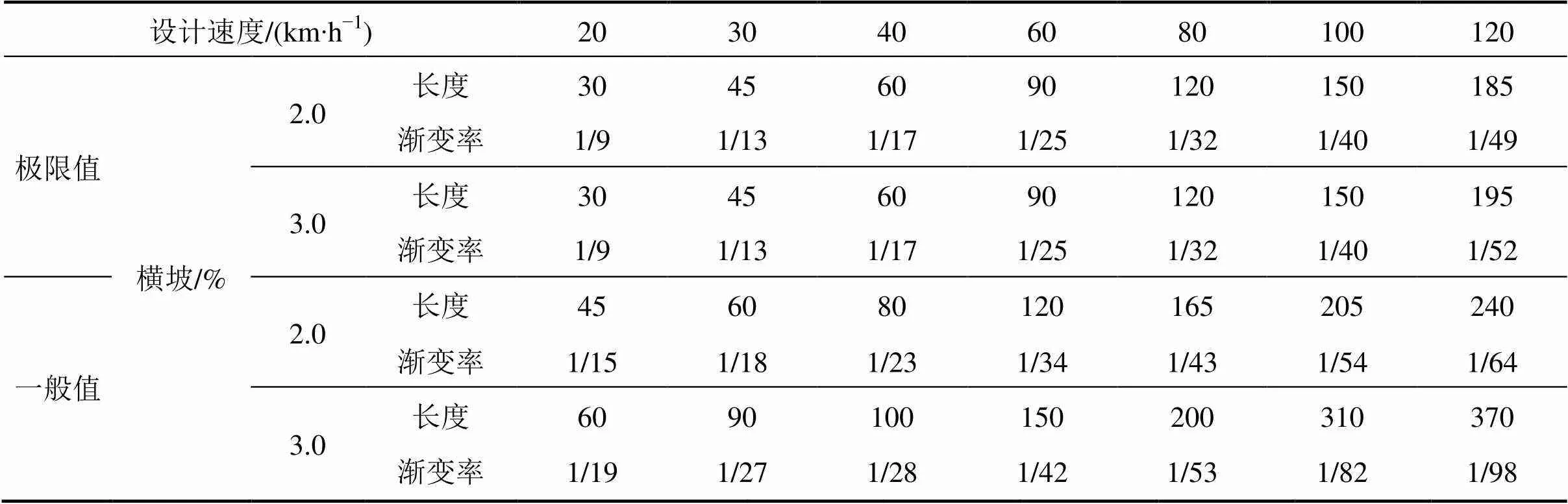
表6 变化一个车道时过渡段长度(m)和渐变率建议值

表7 变化一个车道时过渡段长度(m)最小值

4 仿真验证

为验证计算结果的合理性和安全性，本文采用CarSim和TruckSim车辆动力学仿真软件对小汽车和大货车在车道数变化处的过渡指标进行仿真验证，采用纵向距离—轨迹偏移曲线进行评价。仿真结果表明小汽车的横向偏移距离均小于大货车，因此使用大货车做为仿真车型，对不同设计速度下的计算模型进行验证，换道轨迹采用前述提出的一次函数修正型正弦曲线换道轨迹。

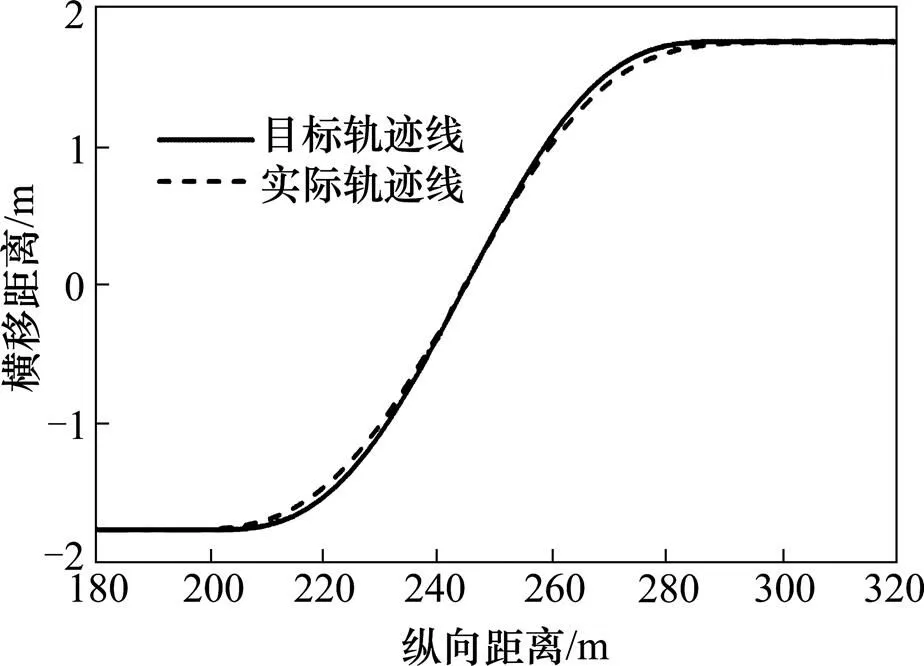
图2 设计速度60 km/h条件下的纵向距离−轨迹偏移曲线

限于篇幅，仅展示设计速度为60 km/h，过渡长度为120 m时的纵向距离—轨迹偏移曲线(图2)。

从图2可以看出：目标轨迹与实际轨迹的最大偏差值出现在纵向距离225 m和270 m处，偏差为0.13 m，根据“综合方差评价法”轨迹偏差标准门槛值为0.3 m[15]，可以认为实际行驶轨迹线与目标轨迹线基本重合，证明采用一次函数修正型正弦曲线换道模型符合车辆换道情况，由此模型计算的车道数变化处过渡段长度及渐变率推荐值也是安全合理的，能满足车辆安全从容变道。

5 结论

1) 本研究基于车辆换道行驶轨迹特征提出了一次函数修正型正弦曲线换道模型，建立了车道数变化过渡段的长度和渐变率计算模型，并根据车辆的受力特性确定了不同设计速度下的横向加速度和横向加速度渐变率。

2) 结合换道模型的特征参数计算，确定了车辆换道的横移宽度与纵向移动距离，研究结果显示车道数变化过渡段的长度和渐变率不仅与设计速度有关，也与横向移动宽度和路面超高横坡有关。然后提出了不同设计速度与超高横坡情况下过渡段的长度和渐变率的建议值。

3) 通过CarSim和TruckSim软件对计算模型进行了仿真验证，结果表明：计算模型符合实际行车轨迹特点，过渡段长度和渐变率的建议值能满足车辆安全从容变道。

[1] 侯赛因. 横断面因素对双车道公路交通安全影响研究[D]. 西安: 长安大学, 2014. HOU Saiyin. Study on the influence of cross sectional factors on traffic safety of two lane highway[D]. Xi’an: Chang’an University, 2014.

[2] JTG B01—2014, 公路工程技术标准[S]. JTG B01—2014, Highway engineering technical standards[S].

[3] JTG D20—2006, 公路路线设计规范[S]. JTG D20—2006, Highway route design code[S].

[4] GB5786—2009, 道路交通标志和标线[S]. GB5786—2009, Road traffic signs and markings[S].

[5] 金珊珊. 公路横断面宽度过渡段技术指标研究[D]. 西安: 长安大学, 2013. JIN Shanshan. Study on the technical index of the transition section of highway cross section[D]. Xi’an: Chang’an University, 2013.

[6] JTG/T B05—2015, 公路项目安全性评价指南[S]. JTG/T B05—2015, Highway project safety evaluation guide[S].

[7] Hesse T, Sattel T. An approach to integrate vehicle dynamics in motion planning for advanced driver assistance systems[C]// Intelligent Vehicles Symposium. IEEE Xplore, 2007: 1240−1245.

[8] 潘兵宏, 张锟, 倪娜, 等. 中间带宽度过渡段的渐变率研究[J]. 公路工程, 2016, 41(1): 94−97. PAN Binghong, ZHANG Kun, NI Na, et al. Study on the gradient rate of transition zone in the middle width[J]. Highway Engineering, 2016, 41(1): 94−97.

[9] CHEN C, ZHANG G, Tarefder R, et al. A multinomial logit model-Bayesian network hybrid approach for driver injury severity analyses in rear-end crashes[J]. Accident Analysis & Prevention, 2015(80): 76−88.

[10] 杨志刚, 戚志锦, 黄燕. 智能车辆自由换道轨迹规划研究[J]. 重庆交通大学学报(自然科学版), 2013, 32(3): 520−524. YANG Zhigang, QI Zhijin, HUANG Yan. Study on trajectory planning of free lane changing of intelligent vehicle[J]. Journal of Chongqing Jiaotong University (Natural Science Edition), 2013, 32(3): 520−524.

[11] Dietz S, Hippmann G, Schupp G. Interaction of vehicles and flexible tracks by co-simulation of multibody vehicle systems and finite element track models[J]. Supplement to Vehicle System Dynamics, 2003, 37(Suppl): 372−384.

[12] 日本道路公团. 日本高速公路设计要领[M]. 西安: 陕西旅游出版社, 1991. Japanese Road Corporation. The design method of Japanese expressway[M]. Xi’an: Shaanxi Tourism Press, 1991.

[13] 杨少伟. 道路勘测设计[M]. 3版. 北京: 人民交通出版社, 2009. YANG Shaowei. Road survey and design[M]. 3rd ed. Beijing: People’s Traffic Press, 2009.

[14] 汤沣泽, 潘晓东, 陈丰. 驾驶员心率变化率与公路横向力系数的相关性[J]. 交通科学与工程, 2015, 31(2): 87−90.TANG Fengze, PAN Xiaodong, CHEN Feng. Corrlation between heart rate change and highwaytrcusverse[J]. Transportation Science and Engineering, 2015, 31(2): 87−90.

[15] Geller D K, Rose M B, Woffinden D C. Event triggers in linear covariance analysis with applications to orbital rendezvous[J]. Journal of Guidance Control & Dynamics, 2012(32): 102−111.

(编辑 蒋学东)

Study on the index of highway lane changing section based on CarSim simulation

PAN Binghong1,2, ZHAO Yuetong1, HUO Yongfu1

(1. School of Highway, Chang’an University, Xi’an 710064, China; 2. Key Laboratory for Special Area Highway Engineering of Ministry of Education, Chang’an University, Xi’an 710064, China)

The length of width transition section and the value of the gradient index design of the highway lanes number changing have important influence on the safety driving. Through the analysis of the vehicle lane number changing characteristics of highway lanes number changing at width transition section, this paper proposed a modified sine curve of lane changing model and established a gradient calculation model of width transition section based on the lane changing trajectory of lane number changing. Through the analysis of characteristic parameters for trajectory model, the lateral movement moving width and longitudinal movement distance of vehicle different design speed and super cross slope are identified, and then put forward width transition length and transition ratio recommended value when the number of lanes is increased or decreased by one. The research results show that the length and transition ratio of width transition section of the lane number changing are not only related to the design speed, but also related to the superelevation cross slope. The proposed value of width transition length and gradient can be used as a reference for the design of width transition section of highway lane number changing in the future.

segment of lanes number changed; width transition; transition ratio; changing lane model; sine curve; superelevation cross slope

10.19713/j.cnki.43−1423/u.2018.10.031

U491.5+4

A

1672 − 7029(2018)10 − 2685 − 07

2017−02−16

广东省交通运输厅科技资助项目(科技-2013-02-059)

潘兵宏(1974−)，男，湖北黄陂人，副教授，博士，从事公路路线，立体交叉研究；E−mail：409291838@qq.com