多孔大断面矩形顶管施工的地层变形特征及演化规律
尹荣申,杨伟超, 2,张平平,邓锷
多孔大断面矩形顶管施工的地层变形特征及演化规律
尹荣申1,杨伟超1, 2,张平平1,邓锷1
(1. 中南大学 土木工程学院,湖南 长沙 410075; 2. 高速铁路建造技术国家工程实验室,湖南 长沙 410075)
基于随机介质理论,计算多孔矩形顶管隧道施工引起的地层变形,通过实际工程验证计算结果的可靠性,分别讨论单个及多孔大断面矩形隧道施工条件下地层的水平位移、倾斜、曲率以及水平变形的演化规律。研究结果表明:沉降范围和沉降累计最大值均呈线性增大,沉降累计最大值的增幅较大,且4孔时均为单孔的2倍;各地层变形累计最大值均在3号顶管中心附近变化最大,水平位移和倾斜累计值均先增加后减小,变形和曲率累计值均呈线性减小;各相邻顶管中间的扰动区域重叠所产生的扰动效应随管节间距和尺寸的变化而变化。
多孔矩形顶管;随机介质理论;地层变形;扰动效应;演化规律
矩形顶管已广泛应用于地铁车站出入口。随着顶管断面尺寸的增大和顶管数量的增加,顶管隧道在施工过程中的地层变形问题也越发突出,特别是对于多孔矩形顶管工程,若其地层变形超过一定限度则会对周围建筑物、路面和地下管线的安全造成严重影响。基于此,诸多学者对顶管隧道施工引起的地层变形等工程问题进行了大量研究,刘大刚 等[1]以随机介质理论为基础,通过对预测公式进行改进,实现双孔平行隧道的地表移动与变形的预测;魏纲等[2−3]利用修正的随机介质理论简化计算公式,计算近距离双线平行盾构施工引起的地表沉降,并考虑沉降曲线的不对称性,对计算参数取值进行探讨;魏新江等[4]对双孔平行顶管施工引起的地表沉降进行了研究,总结出一种根据后施工顶管计算地表沉降的方法;喻军等[5]针对顶管施工造成的环境影响问题,采用数值模拟软件对不同施工参数条件下其对环境产生的影响进行模拟分析;谷拴成等[6]利用随机介质理论预测地表沉降量,并运用弹性力学理论将预测计算所需参数进行量化计算,并对影响其大小的各个因素针对施工环境进行优化;时亚昕等[7]开发了隧道施工引起的地表移动及变形预测系统,并对预测公式进行改进,预测大断面分部开挖引起的地表移动及变形;胡斌等[8]对随机介质理论公式进行简化,对区间各典型断面进行位移反分析,得到隧道断面收敛半径和主要影响角。上述大部分研究均是针对单个或双线圆形隧道地层变形的研究,而对于矩形隧道地层变形的研究,刘宝琛等[10−12]虽对随机介质理论用于单个矩形隧道施工引起的地表变形计算进行了相关推导与讨论,但关于多孔矩形顶管隧道的地层变形及演化规律的研究很少提及。因此,对多孔矩形顶管隧道施工引起的地层变形及其演化规律进行研究具有重要意义。本文以随机介质理论为基础,分析单个矩形顶管施工引起的地层变形特征,并进一步分析从双孔到4孔等多孔顶管顶进过程中地表沉降、倾斜、弯曲以及水平位移、变形等变形指标的演化过程,研究结果对指导具体工程施工具有一定参考价值。
1 随机介质理论
1.1 单元开挖引起的地表变形
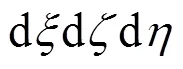
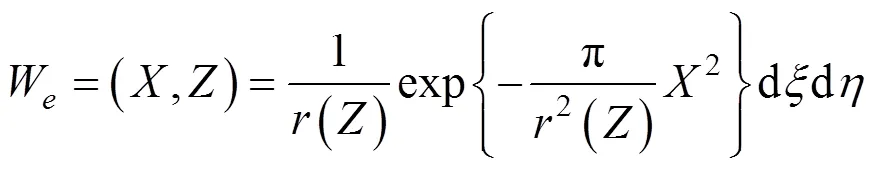
式中:r(Z)为单元开挖在Z水平上的主要影响半径,,tanβ为主要影响角的正切值。
在平面应变情况下,假定土体不可压缩时,土体水平位移(,)为:
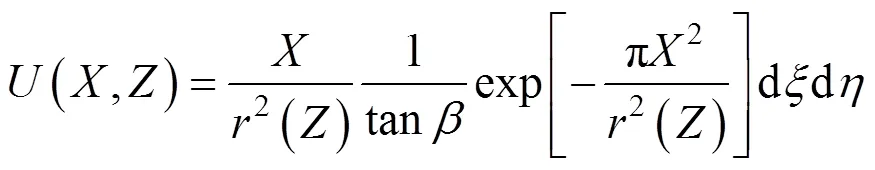
在实际施工时,隧道开挖完成后,开挖空间会发生变形。假设开挖平面区域变形后成为,则上述地表沉降公式即可变形为:
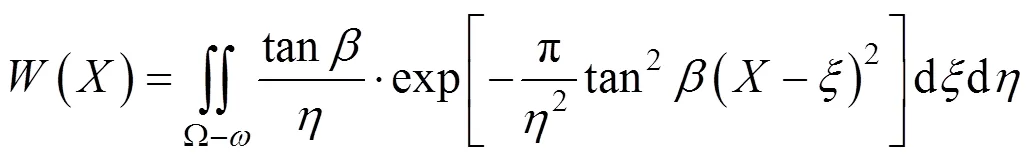
隧道周边土体水平位移变形为:
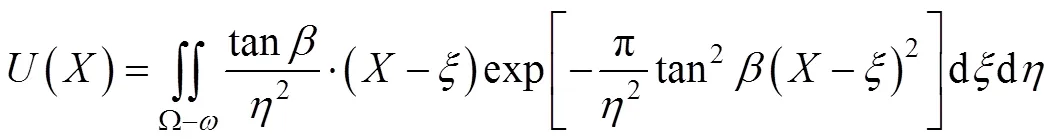
1.2 单个矩形顶管施工引起的土体变形
当顶管开挖断面为矩形时,假设隧道中心线距地表深度为,隧道开挖初始宽度为,开挖高度为,则Ω=∙,假定隧道开挖后产生变形为均匀收缩变形,断面收缩量为Δ,如图2所示,则矩形顶管开挖引起的地表下沉公式可表示为:
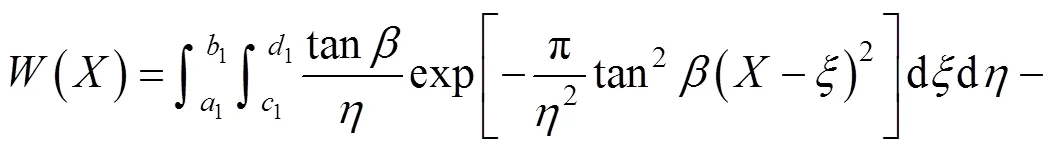
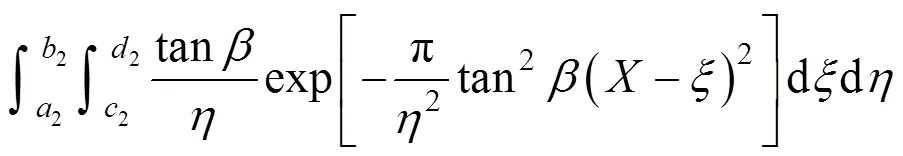
式中:二重积分上下限1,1,1,1,2,2,2和2分别为1=−/2,1=−/2,1=−/2,1=+/2;2=−(2Δ)/2,2=−(2Δ)/2,2=−(2Δ)/2,2=+(2Δ)/2;tan为主要影响角的正切,的取值由隧道开挖所处的地层条件决定。
同理,可按上述二重积分上下限分别对由地表沉降所引起的土体倾斜、弯曲曲率以及水平位移所引起的水平变形分别按下式进行计算:
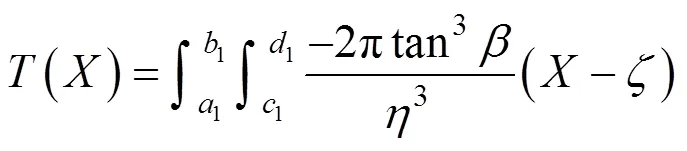
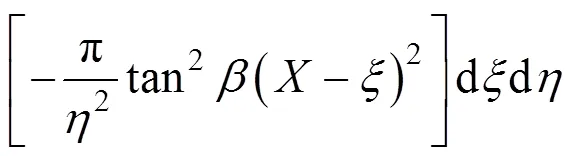
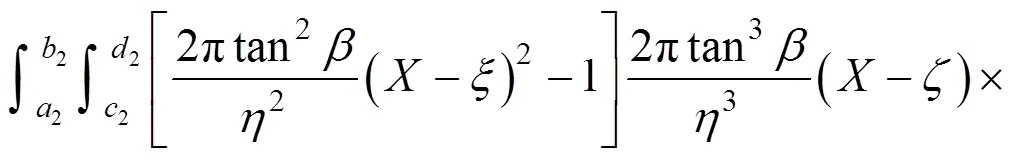
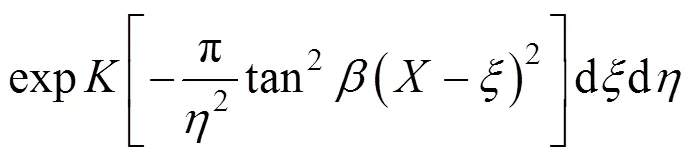
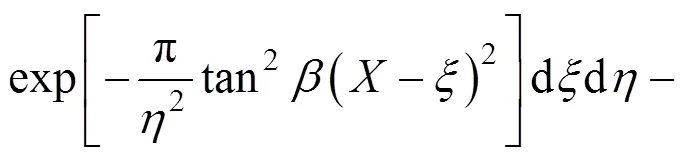
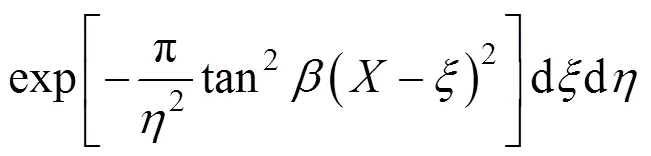
1.3 参数的确定
1.3.1 主要影响角
主要影响角的正切tan的计算,采用随机介质理论中目前常用的Knothe[13]公式来计算:
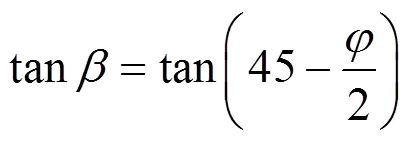
式中:φ为土层内摩擦角。
1.3.2 土体收缩量Δ
Δ为隧道开挖后周围土体收缩量,本文采用韩煊[11]通过反分析计算提出的近似公式计算:
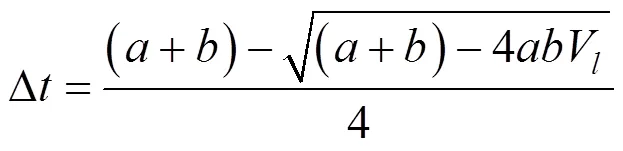
式中:V为地层损失率,地层损失率取值根据经验值[14]确定;和分别为矩形顶管的宽和高。
需要指出的是,隧道断面的收敛形式受多种复杂因素的影响,如地应力分布、地层均匀性、土的各向异性、施工步骤和工艺等,图2所示的只是一种理想状况下的假定,不能代表所有情况。
1.4 多孔矩形顶管施工引起的土体变形
根据叠加原理,由双孔(1号和3号)顶管施工所引起的总的地表下沉(以施工工序1342为例)为:
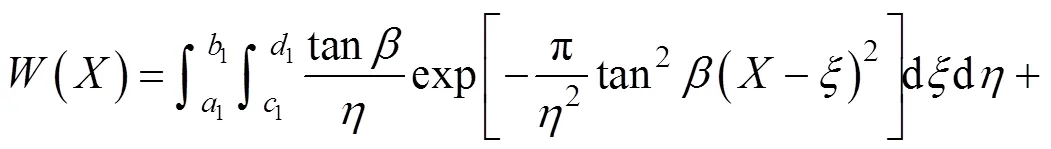
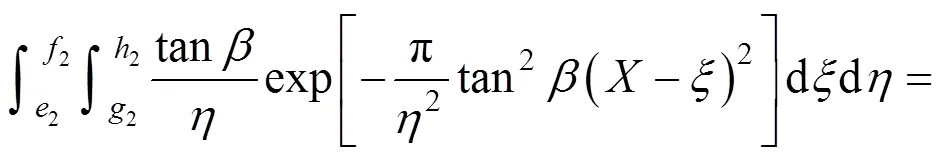
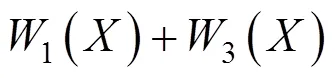
式中:1,1,1,1,1,1,1,1,2,2,2,2,2,2,2和2均为积分上下限,其他符号意义同式(5)。
当顶管数量增加至3孔(1号,3号和4号)时,引起的总地表沉降为:
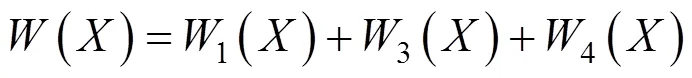
当顶管数量增至4孔或更多时,由隧道施工所导致的地表下沉()和地表水平位移()为:
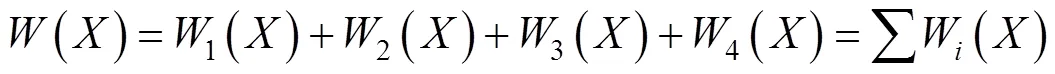
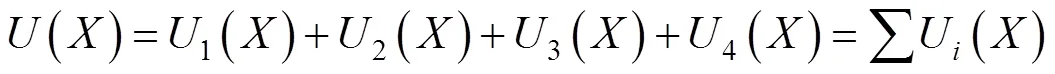
同理,对于多孔矩形顶管,由地表不均匀沉降而导致的地表点的倾斜(),曲率()和不均匀的水平位移所引起的地表点的水平变形()的计算公式如下:
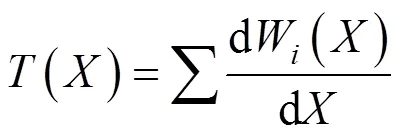
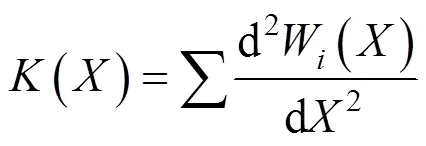
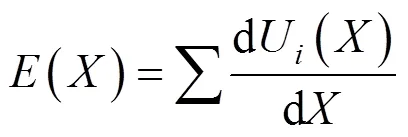
式中:=1,2,3,4…为所开挖顶管的数量。
1.5 工程实例验证
1.5.1 工程概况
郑州市下穿中州大道顶管隧道工程全长105 m,按4孔平行布置,管节间净间距为1 m;两边2孔为非机动车道,管节尺寸7.50 m×5.40 m(宽×高),中间2孔为机动车道,管节尺寸10.10 m×7.25 m(宽×高);管片厚度55 cm,长度为1.5 m,顶管管节模型如图3所示。顶管上覆土层为4.0 m,主要为粉土层,具体岩层参数如表1所示。

图3 顶管管节模型图

表1 岩层主要物理学指标
1号和4号顶管隧道埋深为6.7 m,穿越土层主要为粉土,主要影响角tan的正切值为0.712,断面收缩半径Δ为15.6 mm;3号和4号顶管隧道埋深为7.625 m,穿越土层为粉土和粉质黏土,主要影响角tan的正切值为0.739,断面收缩半径Δ为21.1 mm;1号和3号顶管中心距离为20.9 m;1号,2号,3号和4号顶管中心距离为9.8 m。
1.5.2 测点布置
为对顶管施工过程中的地面沉降变化进行观测,从始发井到接收井共设15个监测断面,每个监测断面设置9个监测点,并在个别断面设置加密测点,具体测点布置如图4所示。
图4 施工测点布置图
1.5.3 实例验证
以实际施工工序1号→3号→4号→2号为例分析多孔矩形顶管隧道开挖时的地层变形规律,即施工时依次施作1号顶管、3号顶管、4号顶管和2号顶管,其中,2号和3号为中间机动车道,1号和4号为两边非机动车道。
通过MATLAB进行二重积分计算可得1号顶管,1号和3号顶管,1号,3号和4号顶管,1号,3号,4号和2号顶管施工完成后的地表沉降预测曲线如图5所示,图中圆点表示沉降实测值。
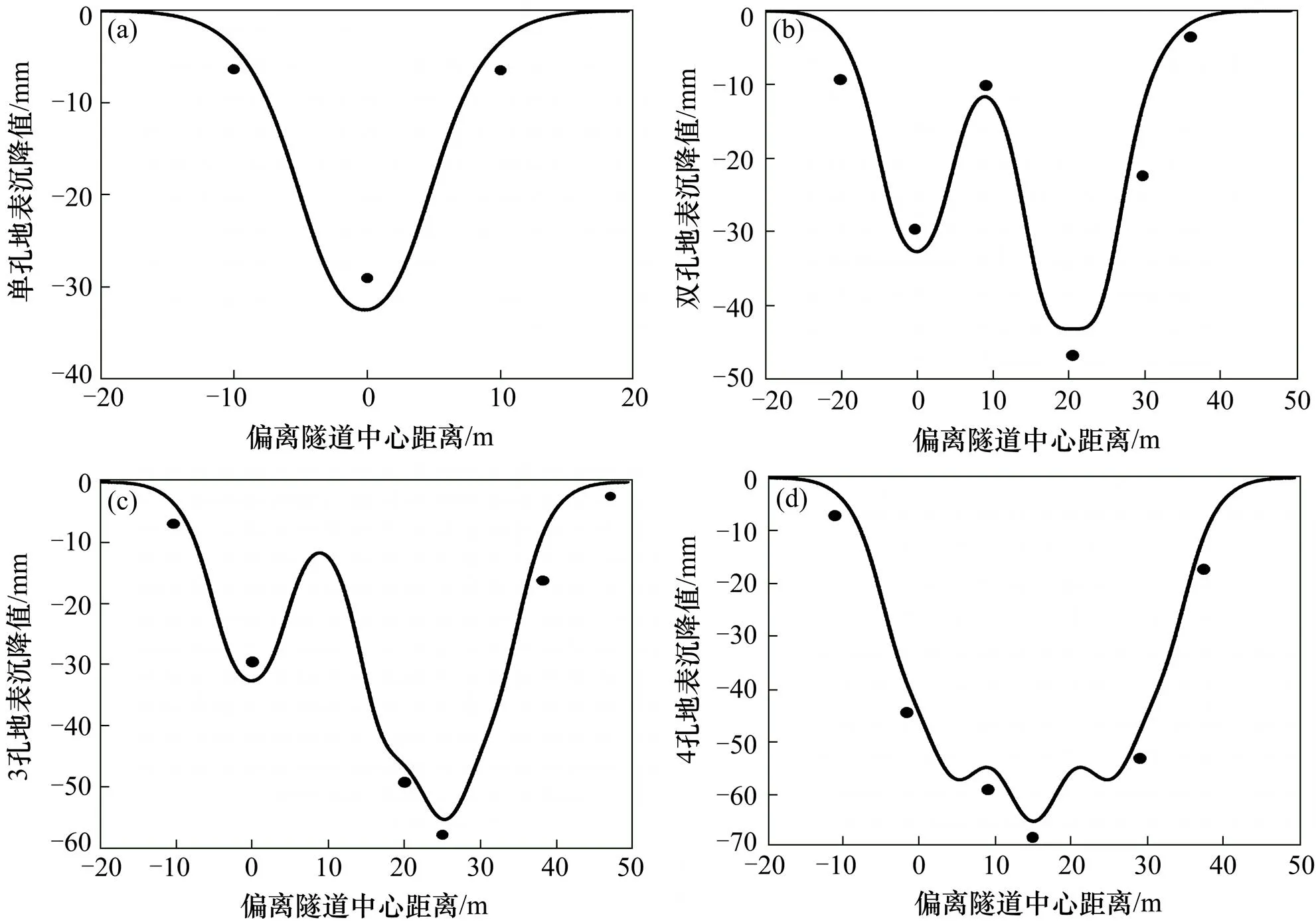
图5 地表沉降预测值与实测值比较
由图5可知:沉降预测值与实测值较为吻合;单孔沉降预测最大值为32.5 mm,实测最大值为29 mm,相差3.5 mm;双孔预测最大值为43 mm,实测最大值为47 mm,相差−4 mm;3孔时预测最大值为56 mm,实测最大值为58 mm,相差−2 mm;4孔时预测最大值为65 mm,实测最大值为68 mm,相差−3 mm;最大值相差均不大,说明采用随机理论预测矩形顶管施工引起的地表沉降是可行的且预测结果较为准确。
2 矩形顶管地层变形分布特性分析
2.1 单个矩形顶管施工引起的地表变形分布规律
单个(1号)隧道施工完成后,各地表变形预测曲线如图6所示。
分析图6可得:
单个隧道施工完成后,各变形的影响范围均在1号隧道轴心两侧20 m的范围内,水平位移最大值8.5 mm出现在1号顶管中心两侧5 m范围内;地表倾斜值的分布规律和水平位移相似,倾斜最大值为4.5 mm/m;水平变形最大值2.1 mm/m出现在1号顶管中心两侧3 m附近;弯曲曲率分布规律和水平变形相似,曲率最大值为1.25 km−1。
2.2 多孔顶管施工引起的地表变形演化规律
2.2.1 地表沉降演化规律
当顶管由单孔增加到4孔时,地表沉降演化曲线如图7所示。
分析图7可得:
1) 沉降槽数量随顶管数量的增加而增加,双孔时沉降槽为2个,尺寸较大的管节沉降槽底部趋于平缓;到3孔时,整体形态和双孔时相似,但距离较近的2个沉降槽相互重合造成中间沉降槽仅显示为一个凸起;到4孔时,沉降槽形态发生较大变化,3个沉降槽紧邻形成一个较大的沉降槽。
2) 沉降范围呈线性增大。单孔时1号顶管为30 m,3号顶管为40 m增加了33%;双孔时为50 m,3孔时55 m,4孔时达到60 m,相比双孔增加了20%,说明沉降范围受顶管尺寸影响较大。
3) 沉降累计最大值呈线性增大。单孔时1号顶管为32.5 mm,3号顶管为42 mm,增加了29%;双孔时沉降最大值为42 mm,3孔时沉降最大值为55 mm,到4孔时沉降最大值达到单孔值的2倍,相比双孔增加了55%,说明多孔顶管沉降最大值受管节尺寸和间距影响较大。
4) 邻近管节的相互干扰主要受管节尺寸和间距影响。双孔时扰动主要发生在1号和3号管节的中部,由于1号和3号管节间距较大,产生的相互干扰较小;到3孔时,3号和4号管节中部扰动区的相互影响比1号和3号管节更明显;到4孔时,相邻顶管之间扰动区域相互重合较多,扰动较大的区域在1号和4号管节中部区域,扰动最大的在2号和3号管节中部区域。

图6 单个顶管地表变形预测曲线

图7 多孔顶管地表沉降演化曲线
2.2.2 水平位移演化规律
当顶管数量由单孔增加到4孔时,水平位移演化曲线如图8所示。
分析图8可得:
1) 双孔时,3号隧道轴心处的曲线不再是直线而是一小段平缓过渡的曲线;3孔时左侧曲线和双孔时相似,右侧曲线在3号和4号顶管中部发生一定变化,具体表现为位移值的普遍增大;4孔时,曲线形态在1号和4号顶管中部发生较大变化,此区域内位移值变化幅度较大。
2) 水平位移累计最大值单孔时1号为8.5 mm,3号顶管为10.5 mm增加了23.5%,说明单个顶管位移最大值随顶管尺寸的增大而增加;双孔时位移最大值10.5 mm,3孔时位移最大值10.5 mm,到4孔时位移最大值11 mm相比双孔增加了5%,位移累计最大值基本无变化,说明多孔时管节间距和尺寸对位移值都有影响,但位移值受顶管尺寸的影响较大。
3) 对于干扰效应,双孔时由于1号和3号顶管距离较远,施工后顶管间相互扰动并不明显;到3孔时,3号和4号顶管距离较近,扰动区域相比双孔时重合较多,此区域产生的相互干扰效应较为明显;到4孔时,两相邻管节间距较小,且中间2号和3号管节尺寸又较大,所以在2号和3号管节中心附近产生的相互干扰效应最为明显。

图8 多孔顶管水平位移演化曲线
2.2.3 地表倾斜演化规律
当顶管数量由单孔增加到4孔时,地表倾斜的演化曲线如图9所示。
分析图9可得:
1) 多孔顶管地表倾斜演化曲线形态和上述水平位移值的变化相似。
2) 倾斜最大值单孔时1号为4.5 mm/m,3号顶管为5.8 mm/m增加了29%,说明单个顶管最大值随顶管尺寸的增大而增加;双孔时倾斜累计最大值5.8 mm/m,到3孔时倾斜最大值5.6 mm/m,到4孔时倾斜最大值5.5 mm/m,多孔顶管倾斜累计最大值逐渐减小。
3) 多孔顶管的地表倾斜曲线相互干扰规律和水平位移相似。
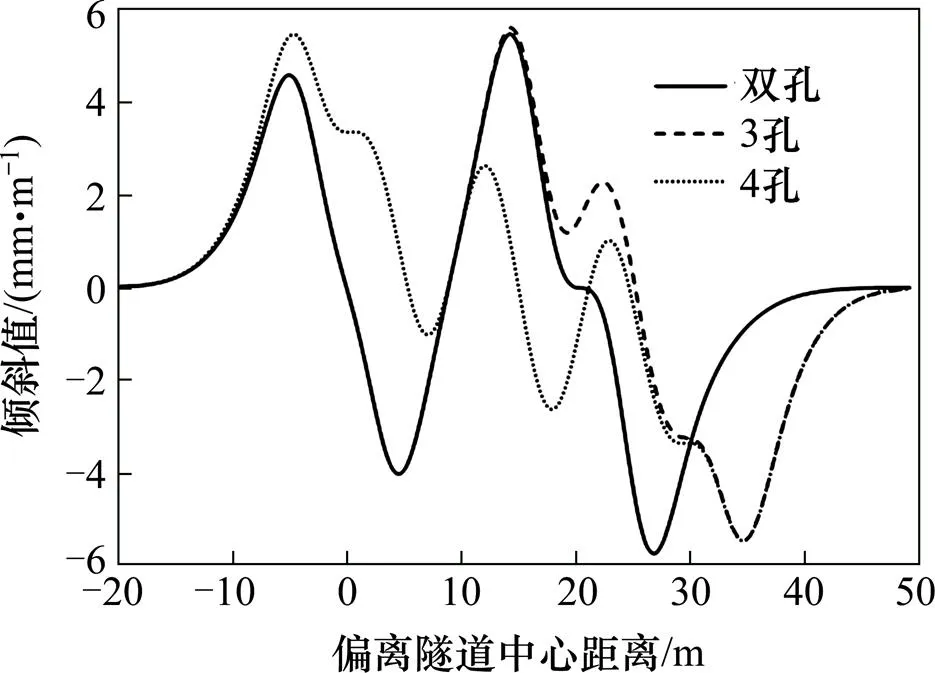
图9 多孔顶管地表倾斜演化曲线
2.2.4 水平变形演化规律
当顶管数量由单孔增加到4孔时,水平变形的演化曲线如图10所示。
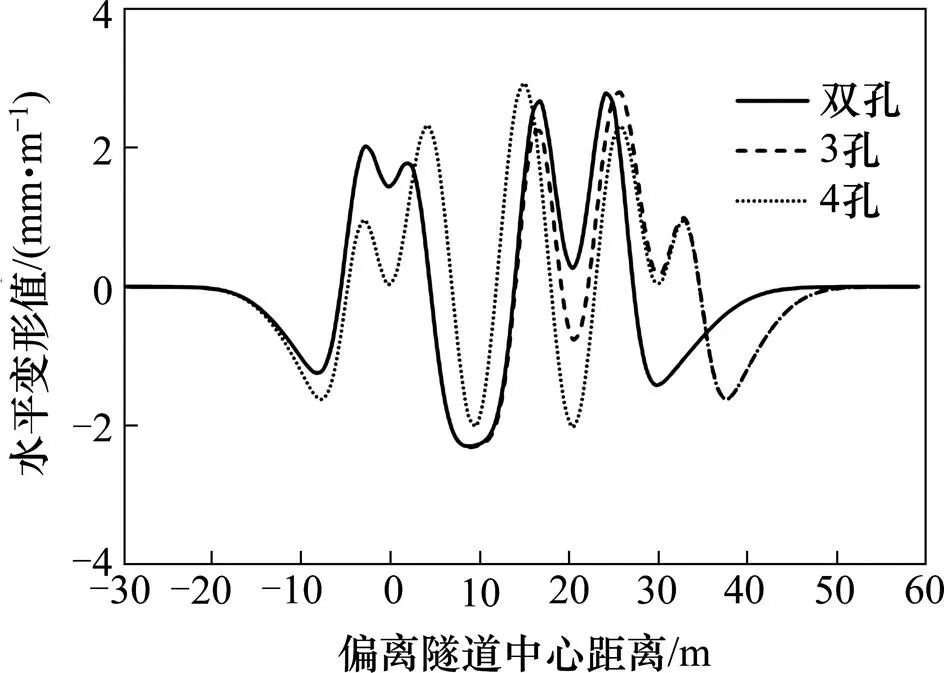
图10 多孔顶管水平变形演化曲线
分析图10可得:
1) 双孔时,1号和3号顶管中部的曲线发生变化,底部为一段平滑的圆弧;3孔时,左侧曲线和双孔时相似,右侧曲线形态在3号和4号顶管中部发生一定变化,具体表现为倾斜值逐渐减小;4孔时,曲线形态在1号和4号顶管中部发生较大变化,整体位移值变化幅度较大。
2) 变形最大值单孔时1号为2.1 mm/m,3号顶管为2.8 mm/m增加了33%,说明单个顶管变形最大值随管节尺寸的增大而增加;双孔时变形累计最大值2.8 mm/m,到3孔时变形累计最大值2.8 mm/m,到4孔时变形累计最大值2.9 mm/m相比双孔增加了3%,多孔顶管水平变形累计值基本无 变化。
3) 对于干扰效应,双孔时1号和3号顶管距离较远,两隧道扰动区虽有相互影响但并不明显;到3孔时,3号和4号隧道距离较近,扰动重合区域变大,产生的相互干扰相对较明显;到4孔时,相邻顶管间距较小扰动区域重合较多、产生的干扰效应比较明显,其中,2号和3号管节间的干扰最为明显。
2.2.5 弯曲曲率演化规律
当顶管由单孔增加到4孔时,弯曲曲率的演化曲线如图11所示。
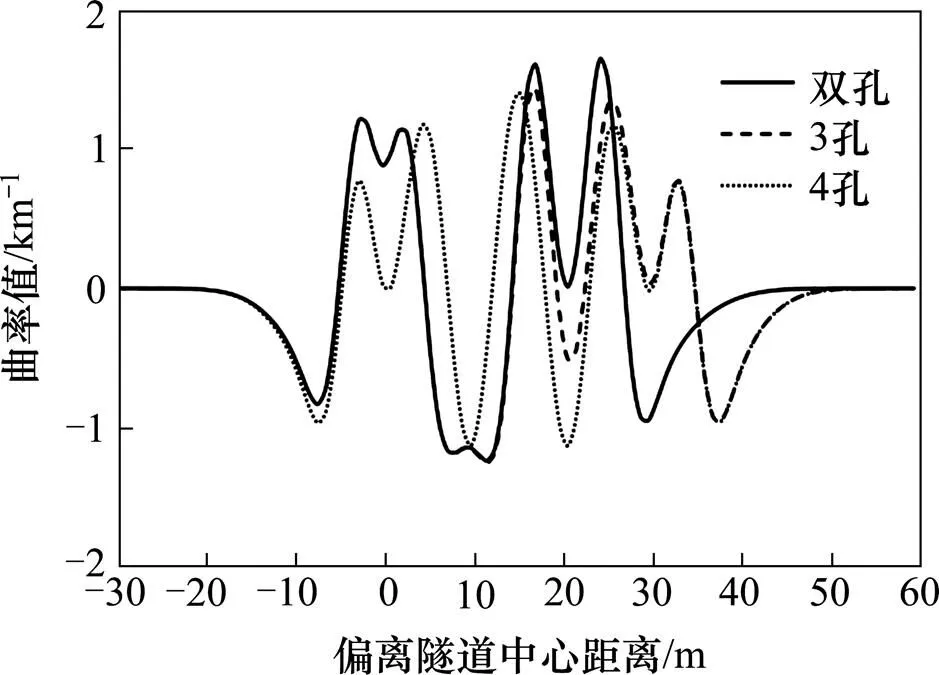
图11 多孔顶管弯曲曲率演化曲线
分析图11可得:
1) 多孔顶管弯曲曲率的演化曲线形态和上述水平变形相似;但是在双孔和3孔时,1号和3号顶管中部的曲线底部不再是一段平滑的圆弧而是一段波浪线。
2) 曲率最大值单孔时1号为1.25 km−1,3号顶管为1.6 km−1增加了28%,说明单个顶管变形最大值随顶管尺寸的增大而增加;双孔时曲率累计最大值1.6 km−1,到3孔时曲率累计最大值1.4 km−1,到4孔时曲率累计最大值1.35 km−1相比双孔减少了16%,多孔顶管曲率累计最大值逐渐减小。
3) 多孔顶管的地表倾斜曲线相互干扰规律和水平位移相似。
3 结论
1) 矩形顶管数量从单孔增加到4孔时,沉降槽形态发生相应变化,具体表现如下:沉降范围呈线性增大,单孔时为30 m,到4孔时增至2倍;沉降累计最大值也呈线性增长,单孔时为32.5 mm,到4孔时增至2倍;沉降累计最大值增加的速度要大于沉降范围。
2) 水平位移和地表倾斜、水平变形和弯曲曲率的演化曲线形态较为相似;对于多孔顶管,各演化曲线形态与累计最大值均受管节尺寸和间距影响;各地层变形累计最大值均在3号顶管中心附近变化最大,水平位移和倾斜累计值均先增加后减小,变形和曲率累计值均呈线性减小。
3) 多孔顶管隧道施工时,相邻隧道间产生的干扰效应随顶管断面尺寸和顶管间距的变化而发生相应的改变:当顶管尺寸均较大或一大一小且距离较近时,引起的相互干扰较强;当顶管尺寸较小且距离较远时,引起的相互干扰较弱。
[1] 刘大刚, 陶德敬, 王明年. 地铁双隧道施工引起的地表沉降及变形的随机预测方法[J]. 岩土力学, 2008, 29(12): 3422−3426. LIU Dagang, TAO Dejing, WANG Mingnian. Stochastic method for predicting ground surface settlement and deformation induced by metro double tube tunneling[J]. Rock and Soil Mechanics, 2008, 29(12): 3422−3426.
[2] 魏纲, 周杨侃. 双线平行盾构开挖引起的地表沉降随机介质预测[J]. 现代隧道技术, 2016, 53(5): 92−99. WEI Gang, ZHOU Yangkan. Stochastic medium prediction for ground settlement induced by double-line parallel shield tunneling[J]. Modern Tunneling Technology, 2016, 53(5): 92−99.
[3] 魏纲, 陈伟军, 魏新江. 双圆盾构隧道施工引起的地面沉降预测[J]. 岩土力学, 2011, 32(4): 991−996. WEI Gang, CHEN Weijun, WEI Xinjiang. Prediction of surface settlement induced by double-o-tube shield tunnel excavation[J]. Rock and Soil Mechanics, 2011, 32(4): 991−996.
[4] 魏新江, 魏纲. 水平平行顶管引起的地面沉降计算方法研究[J]. 岩土力学, 2006, 27(7): 1129−1132. WEI Xinjiang, WEI Gang. Study on calculational method of ground settlement induced by level parallel pipe jacking[J]. Rock and Soil Mechanics, 2006, 27(7): 1129−1132.
[5] 喻军, 龚晓南. 考虑顶管施工过程的地面沉降控制数值分析[J]. 岩石力学与工程学报, 2014, 33(增1): 2605−2610. YU Jun, GONG Xiaonan. Numerical analysis of surface settlement control considering pipe jacking construction process[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(Suppl 1): 2605−2610.
[6] 谷拴成, 李敏. 西安地铁盾构施工地表沉降随机介质预测研究[J]. 铁道工程学报, 2014(3): 110−116. GU Shuancheng, LI Min. Study and prediction of surface settlement in Xi’an subway during shield construction based on stochastic medium theory[J]. Journal of Railway Engineering Society, 2014(3): 110−116.
[7] 时亚昕, 陶德敬, 王明年. 大断面浅埋暗挖隧道施工引起的地表移动及变形预测[J]. 岩土力学, 2008, 29(2): 465−460. SHI Yaxin, TAO Dejing, WANG Mingnian. Prediction of ground surface movement and deformation in constructing large cross-section tunnel by shallow- burying and hidden-digging method[J]. Rock and Soil Mechanics, 2008, 29(2): 465−460.
[8] 胡斌, 刘永林, 唐辉明, 等. 武汉地铁虎泉—名都区间隧道开挖引起的地表沉降研究[J]. 岩石力学与工程学报, 2012, 31(5): 908−913. HU Bin, LIU Yonglin, TANG Huiming. Research on ground subsidence due to tunnel excavation in Huquan—Mingdu section of Wuhan subway[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(5): 908−913.
[9] 刘宝琛. 随机介质理论及其在开挖引起的地表下沉问题中的应用[J]. 中国有色金属学报, 1992, 2(3): 8−14. LIU Baochen. Stochastic medium theory and its application in surface subsidence caused by excavation[J]. Transactions of Nonferrous Metals Society of China, 1992, 2(3): 8−14.
[10] 刘宝琛, 张家生. 近地表开挖引起的地表沉降的随机介质方法[J]. 岩石力学与工程学报, 1995, 14(4): 289−296. LIU Baochen, ZHANG Jiasheng. Stochastic method for ground subsidence due to near surface excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 1995, 14(4): 289−296.
[11] 韩煊. 隧道施工引起地层位移及建筑物变形预测的使用方法研究[D]. 西安: 西安理工大学, 2006. HAN Xuan. The analysis and prediction of tunneling-induced building deformations[D]. Xi’an: Xi’an University of Technology, 2006.
[12] 施成华, 黄林冲. 顶管施工隧道扰动区土体变形计算[J]. 中南大学学报, 2005, 36(2): 323−328. SHI Chenghua, HUANG Linchong. Calculation of soil deformation in area of disturbance due to pipe-jacking construction[J]. Journal of Central South University (Science and Technology), 2005, 36(2): 323−328.
[13] Knothe S. Observations of surface movements under influence of mining and their theoretical interpretation [C]// Proc European Conf. on Ground Movement, 1957: 210−218.
[14] O’Reilly M P, New B M. Settlements above tunnels in the United Kingdom-their magnitude and prediction[C]// Proc Tunneling 82, Institution of Mining and Metallurgy, London, 1982: 173−181.
[15] New B M, Bowers K H. Ground movement model validation at the Heathrow express trail tunnel[M]. New York: Springer, 1994: 301−329.
(编辑 阳丽霞)
Stratum deformation characteristics and evolution laws induced by porous large section rectangular pipe jacking construction
YIN Rongshen1, YANG Weichao1, 2, ZHANG Pingping1, DENG E1
(1. School of Civil Engineering, Central South University, Changsha 410075, China; 2. National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China)
Based on stochastic medium theory, the deformation of the strata caused by the construction of porous rectangular tunnel is calculated, and then through the actual project to verify the reliability of the method, the settlement characteristics of strata under the construction condition of single large section rectangular tunnel and the evolution of horizontal displacement, inclination, bending and horizontal deformation of the strata under the construction of porous tunnel are discussed respectively. The results show that the settlement range and settlement cumulative maximum all show a linear increase, the cumulative maximum value of settlement increases greatly ,and the maximum value at four is two times of single; The accumulative maximum values of deformation in each layer changes the most near the No.3 pipe jacking center, horizontal displacement and tilt cumulative values are increased first and then decreased, deformation and curvature cumulative values are linearly reduced; The disturbance produced by the overlapped disturbance region in each adjacent pipe jacking varies with the pitch and size of the pipe section.
porous rectangular pipe jacking; stochastic medium theory; stratum deformation; disturbance effect; evolution laws
10.19713/j.cnki.43−1423/u.2018.10.020
U455.47
A
1672 − 7029(2018)10 − 2597 − 09
2017−07−18
国家自然科学基金资助项目(140826)
杨伟超(1978−),男,河南许昌人,讲师,博士,从事隧道及地下工程方面的教学与科研工作;E−mail:weic_yang@163.com

