基于矩法的CRTSⅡ型轨道板横向抗弯承载力时变可靠度研究
邹 红,卢朝辉,余志武
(中南大学 土木工程学院,湖南 长沙 410075)
截至2017年底,我国高速铁路运营里程突破2.5万km。为了践行工后“零沉降”建设理念,一般在土质不良地段采用以桥代路的方法控制工后沉降,其中CRTSⅡ型无砟轨道简支箱梁结构体系占整个线路桥梁的近50%[1]。
简支箱梁上CRTSⅡ型无砟轨道板起着传递、分散外界荷载的作用。文献[2]要求桥上无砟轨道结构设计使用年限为60年,这就要求60年内轨道板结构有完成预定功能(耐久性、安全性、适用性)的能力,轨道板安全承载力失效将严重影响铁路的正常运输及高速列车的运行安全。文献[3]采用3种无砟轨道列车荷载弯矩计算模型,分别计算了列车荷载作用下轨道板横向最大正、负弯矩值,从计算精度和简便性等方面对比3种模型计算列车荷载弯矩的优劣,推荐将弹性地基梁-板模型作为无砟轨道列车荷载弯矩计算模型。文献[4]采用Westgaard公式分析轨道板在正、负温度梯度作用下的弯矩。
在施工建设期以及运营过程中,CRTSⅡ型轨道板承载能力会受到材料自身强度、列车荷载以及环境作用等随机不确定性的影响。文献[5]规定了轨道结构在设计年限内安全性、适用性等应当具备的可靠度水准。文献[6]考虑列车荷载与环境荷载随机不确定性条件,提出基于FORM法的CRTSⅡ型轨道板横向抗裂可靠度分析方法。文献[7]考虑列车竖向轮轨力、地基系数等随机不确定性条件,提出基于蒙特卡洛直接抽样法的CRTSⅡ型轨道板横、纵向抗裂可靠度分析方法。通过FORM法、蒙特卡洛直接抽样法进行轨道结构可靠度分析分别存在反复迭代确定验算点[8]、计算量大等不足,因此选择一种计算过程相对简便、计算结果精度满足要求的轨道板结构可靠度计算方法便显得尤为重要。
鉴于此,本文发展轨道结构可靠度分析的四阶矩方法。借助单联宽轨枕模型发展了考虑荷载与环境共同作用的CRTSⅡ型轨道板横向抗弯承载力抗力时变模型,结合列车荷载横向弯矩与温度翘曲弯矩,建立简支箱梁上CRTSⅡ型轨道板横向抗弯承载力的极限状态函数;假定轨道板结构处于3种抗力衰减服役环境中,分别用7点估计一维减维法求解函数的前四阶矩,采用四阶矩可靠度公式求出可靠度指标及相应失效概率。
1 列车荷载与温度作用下轨道板横向抗弯承载力时变极限状态函数
文献[9]认为,考虑抗力衰减的工程结构抗弯承载力可靠度分析中,极限状态函数(功能函数)可表述为
Z(t)=r(t)MR0-MS
(1)
式中:MR0为轨道板横向抗弯初始承载力;t为轨道结构服役时间;r(t)为抗力衰减函数;MS为外界荷载作用弯矩,包括列车荷载横向弯矩Mv和环境作用弯矩Mw。
1.1 轨道板横向抗弯承载力时变抗力计算
整个轨道结构服役期间,受到各种抗力衰减因素(结构疲劳累积损伤、盐雾侵蚀、混凝土碳化等)[1]的影响,轨道板承载力呈下降趋势。
文献[10]认为,抗力衰减因素本身就是随着时间变化的随机过程,较难定量描述,并且各因素之间还可能存在复杂的相关关系,因此结构抗力随着时间的变化是复杂的随机过程。一般来说,结构抗力随时间的变化是非平稳随机过程,为了计算上的简化和实用性,可将非平稳随机过程平稳化,即将时变抗力r(t)MR0表示为
r(t)MR0=MR0(X1,t)=(1-k1t+k2t2)MR0
(2)
式中:X1=[x1x2…xn1]T,x1,x2,…,xn1分别为r(t)MR0中随机变量参数(t除外),n1为r(t)MR0中变量个数;k1、k2为系数。
文献[11]在单联轨枕基础上,充分考虑横向预应力筋以及普通钢筋的受力情况,建立受力平衡方程,结合文献[12]得出轨道板横向抗弯初始承载力计算式为
(3)
假定轨道结构处于不同的服役环境中,抗力衰减因素对轨道板作用强度不同。文献[13]基于工程结构的3种不同服役环境,提出3种抗力退化速率,即低速退化、中等退化以及严重退化,分别对应式(2)中k1、k2的不同取值。
1.2 列车荷载作用下轨道结构横向弯矩分析模型
文献[14]认为,由于无砟轨道各结构层在厚度方向的尺寸远小于横、纵方向的尺寸,且荷载作用下的挠度远小于其厚度,故将其视为梁-板结构体系,如图1所示。
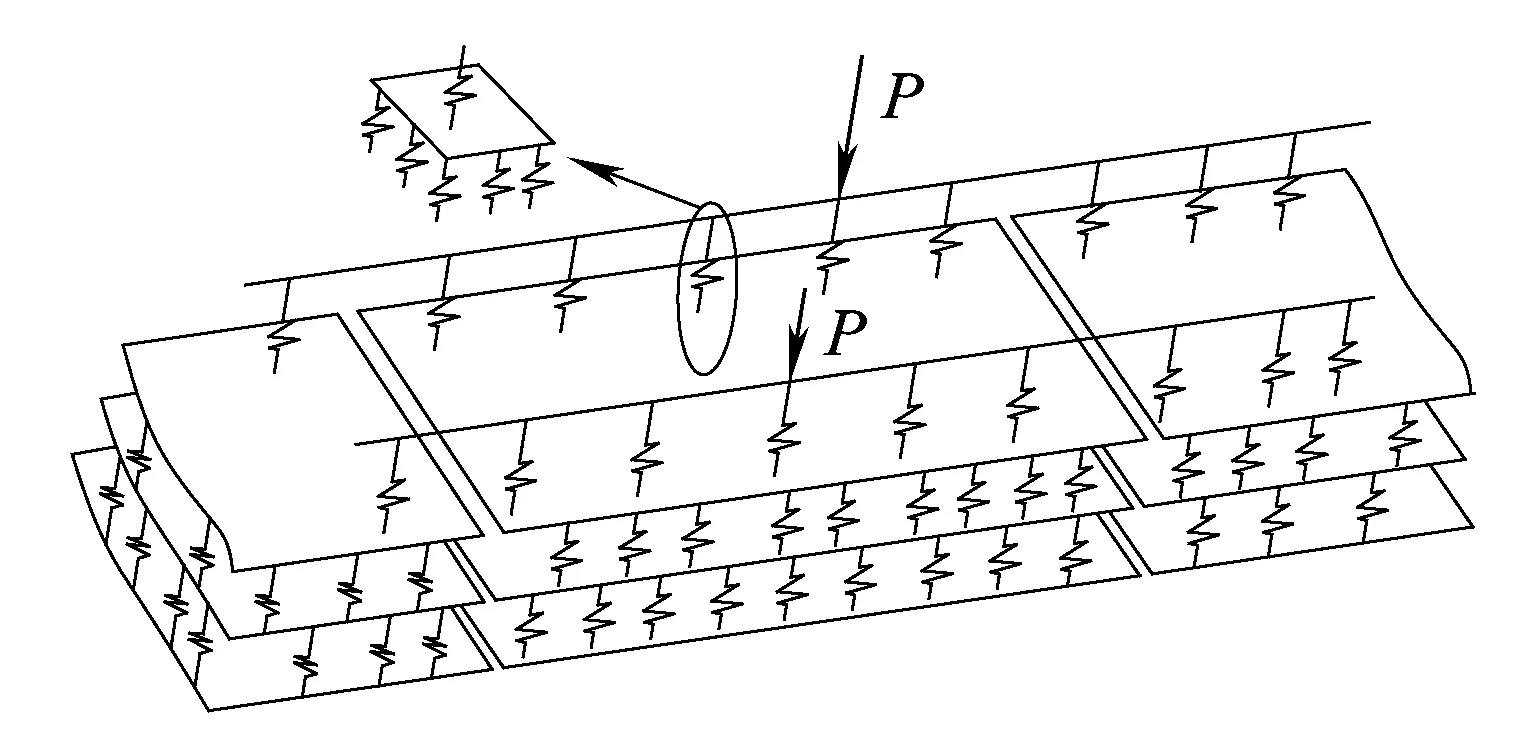
图1 轨道结构体系受力
鉴于此,在建立有限元分析模型时,扣件采用三向弹簧模拟[15];CA砂浆层采用竖向弹簧模拟,其刚度按照串联关系计算得到[16];下部基础采用Winkler弹性地基模型模拟;桥面支撑简化为竖向弹簧,弹簧刚度等于桥梁上地基系数除以离散弹簧个数;用ANSYS软件分析Mv时,把列车竖向轮轨力P等看成随机变量,即
Mv=Mv(X2)=Mv(P,…)
(4)
式中:X2=[xn1+1xn1+2…xn1+n2]T,xn1+1,xn1+2,…,xn1+n2分别为Mv中随机变量;n2为Mv中变量个数。
1.3 温度作用下轨道结构的横向弯矩计算模型
轨道结构在运营期内,会受到温度梯度荷载作用,文献[6]基于Westgaard公式将温度梯度翘曲弯矩简化为
Mw=Mw(X3)=KtT
(5)
式中:X3=[xn1+n2+1xn1+n2+2…xn1+n2+n3]T,xn1+n2+1,xn1+n2+2,…,xn1+n2+n3分别为Mw中随机变量;n3为Mw中变量个数;T为温度梯度;Kt为温度弯矩系数。
将式(2)~式(5)代入式(1)可以得到轨道板t时刻横向抗弯极限状态函数为
(6)
2 轨道板横向抗弯承载力可靠度分析的四阶矩方法
2.1 点估计计算功能函数前四阶矩的基本思想
对于功能函数G(X),可以采用标准正态空间上的m点估计函数的前四阶矩
(7)
(8)

(9)

(10)


(11)
Gμ=G(μ)
(12)
Gi=G[μ1,μ2,…,μi-1,T-1(ui),μi+1,…,μn]
(13)
式中:μ=[μ1μ2…μn]T,μ1,μ2,…,μn为随机变量均值;ui(i=1,2,…,n)为标准正态空间随机变量;Gi为仅含有参数ui的单变量函数。
G(X)前四阶矩可表示为
(14)
(15)
(16)
(17)

(18)
(19)
(20)
(21)
式中:uik(k=1,…,m;i=1,2,…,n)是ui的第k个估计点;T-1(uik)是第i个随机变量的第k个逆正态转换值;pk是相应的权重。若采用标准正态空间中的7点估计,其估计点值uik及权重pk[18]为
(22)
2.2 轨道板横向抗弯承载力时变功能函数的前四阶矩计算
根据式(13)有
(23)
Gμ=MR0(μ1,…,μn1,t)-Mv(μn1+1,…,μn1+n2)-
Mw(μn1+n2+1,…,μn1+n2+n3)
(24)
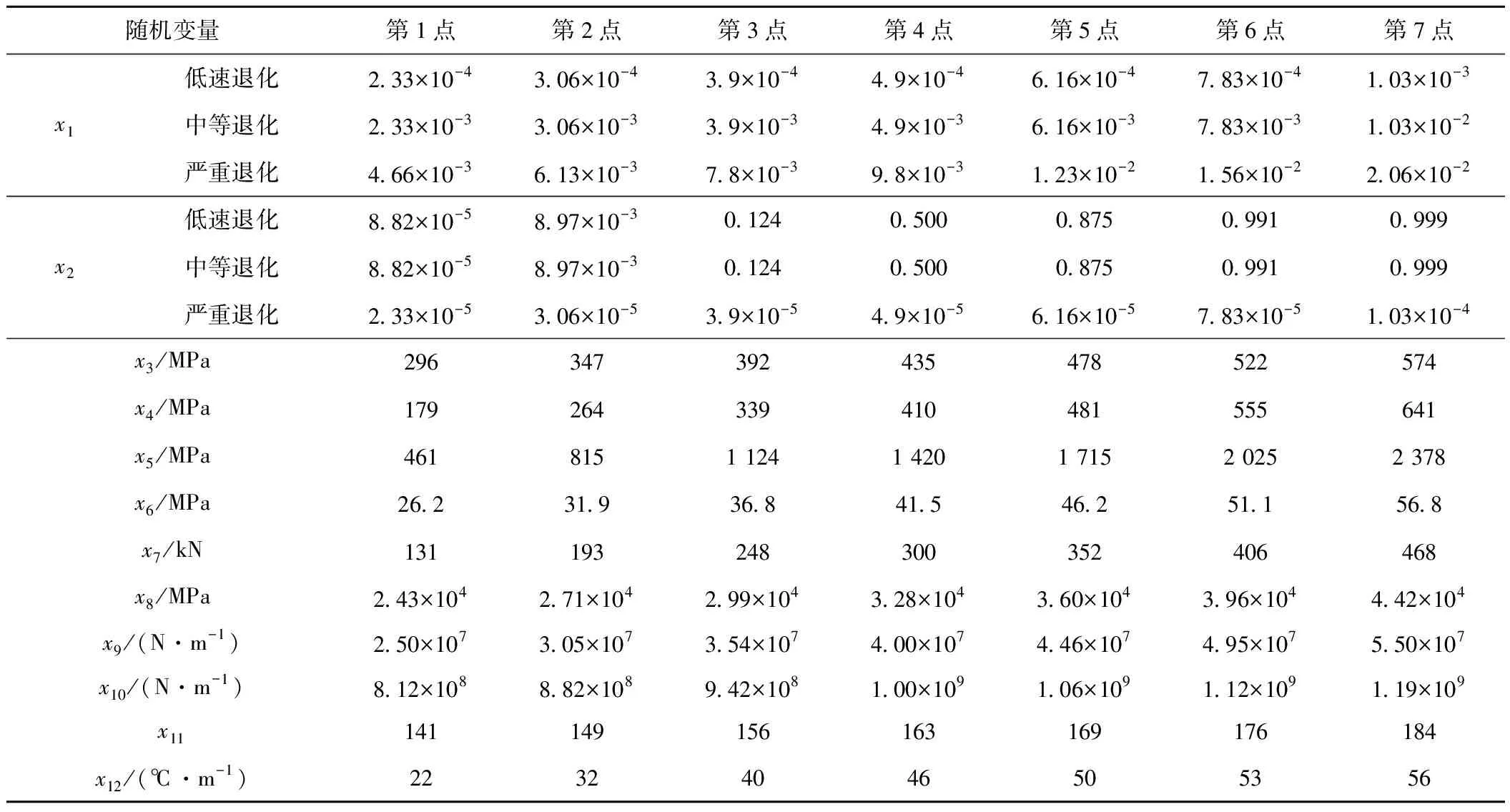
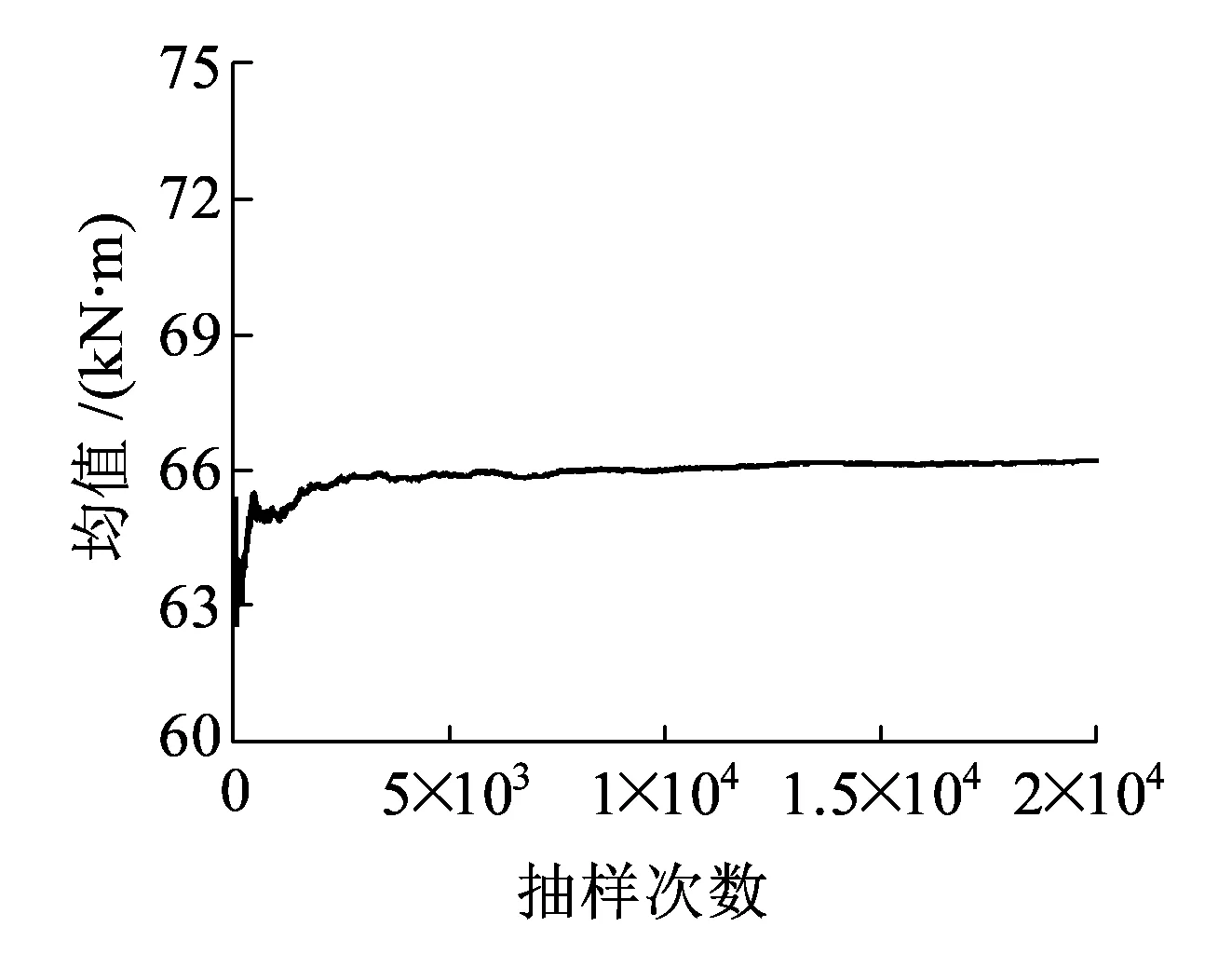
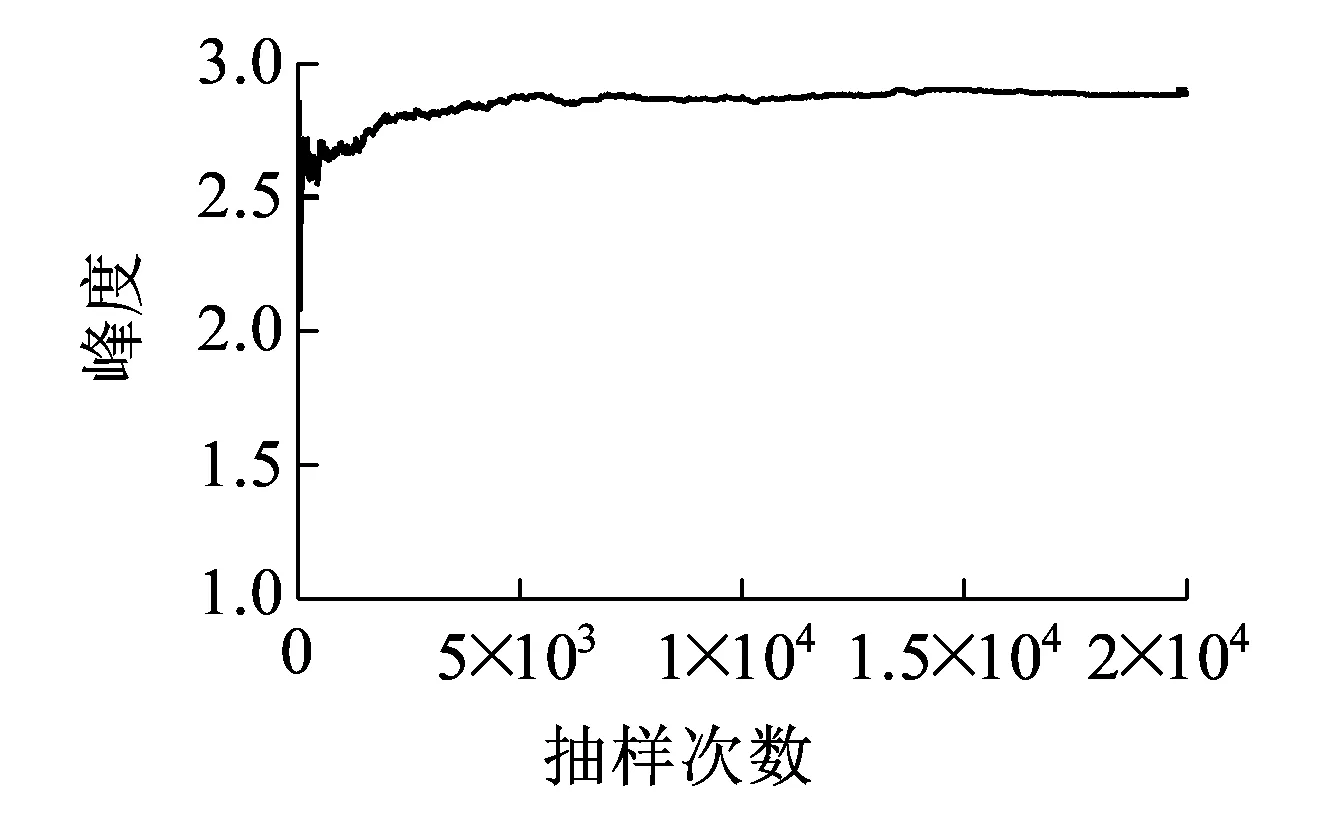
式中:T-1(ui)为式(6)中随机变量xi的逆正态转换值;μ1,μ2,…,μi-1,μi+1,…,μn1+n2+n3分别为式(6)中所有随机变量(不含第i个)的均值;MR0(μ1,…,μi-1,T-1(ui),μi+1,…,μn1,t)为当xi取逆正态转换值(1≤i≤n1),其余变量取均值时式(2)的值;Mv(μn1+1,…,μi-1,T-1(ui),μi+1,…,μn1+n2)为当xi变量取逆正态转换值(n1 基于梁-板有限元模型利用ANSYS软件分析Mv(μn1+1,μi-1,T-1(ui),μi+1,…,μn1+n2)时,考虑到轨道板间受力、变形的对称性,取一块轨道板对其进行受力分析,梁-板有限元模型如图2所示(红色箭头表示列车竖向轮轨力):其中3个方向的扣件刚度分配值如图3所示,其计算结果可以用etable,mx,smisc,4命令提取。 图2 梁-板有限元分析模型 图3 轨道板细部A(单位:mm) 得到功能函数的前四阶矩后,采用式(25)和式(26)可以计算四阶矩可靠度指标及失效概率[19] (25) Pf=Φ(-β4M) (26) 式中 (27) 为了保证l2存在,根号内的数必须为正值,因而必须满足 (28) 参考原铁道第三勘察设计院集团有限公司设计的时速250 km的客运专线CRTSⅡ型板式无砟轨道轨道板结构设计图[20],如图4所示。整块轨道板长为6 450 mm,厚度为200 mm,宽度为2 550 mm;每一块轨道板之间用直径20 mm的螺纹钢连接[21];混凝土强度等级为C55;横、纵钢筋交叉口采用绝缘设计;每块轨道板由10块单联轨枕组成;单联轨枕上、下层分别设置4根HRB500级钢筋;形心偏下10 mm处设置6根φ10预应力钢筋。 图4 CRTSⅡ型轨道板俯视图(单位:mm) 根据表1随机变量的分布特征, 用式(22)标准正态空间的7点估计值求解每个随机变量经过T-1(uim)逆正态转换之后的7点估计值,见表3。 表1 随机变量分布特征 表2 常量取值 表3 随机变量7点逆正态转换值 利用2.2节建立的轨道结构体系梁-板有限元模型,分析Mv(X2)时用到的相关参数,见表4。 表4 梁-板有限元模型参数取值 在ANSYS软件中,先将列车荷载x7取表4中7点估计值,x8、x9、x10取表1中均值,Mv(T-1(u7m),μ8,μ9,μ10)的7个值;同理分别得到Mv(μ7,T-1(u8m),μ9,μ10)、Mv(μ7,μ8,T-1(u9m),μ10)、Mv(μ7,μ8,μ9,T-1(u10m))的7个值,见表5。 表5 Mv(x7,x8,x9,x10)的7点有限元解 N·m 当x7、x8、x9、x10全部取表1中均值时,Mv(μ7,μ8,μ9,μ10)=11 156 N·m。 3.2.1不同服役环境中轨道板结构初始状态单变量参数函数前四阶矩的计算 对于初始状态,即t=0时,不同退化环境下功能函数相同:将表1中xi均值、表2常数项、Mv(μ7,μ8,μ9,μ10)、Mw(μ11,μ12)代入式(24)得Gμ=66 395 N·m;将G1、表2中x1的7个逆正态转换值、表2常数项、Mv(μ7,μ8,μ9,μ10)、Mw(μ11,μ12)、式(22)相应权重全部代入式(18)~式(21)可计算得到G1的前四阶矩分别为:66 395、0、0、0 N·m。 同理可得到Gi(i=2,…,3,…,12)的前四阶矩,见表6。 表6 轨道板结构初始状态单变量参数函数Gi前四阶矩 3.2.2轨道板结构初始状态功能函数前四阶矩及可靠度计算 将Gμ、表6中的Gi(i=1,2,…,12)均值代入式(14),得到μG=66 171 N·m; 将表5中Gi标准差代入式(15),得到σG=12 862 N·m; 将表5中Gi标准差、偏度代入式(16),得到α3G=-0.121; 将表5中Gi标准差、峰度代入式(17),得到α4G=2.826。 利用ANSYS软件PDS模块技术,取t=0,采用蒙特卡洛直接抽样法对式(6)计算2万次,利用Excel对数据进行统计,得到轨道板结构初始状态功能函数前四阶矩的变化过程,如图5所示。 用蒙特卡洛有限元法统计分析四阶矩时,抽样次数越多结果越精确,但耗时会增加,不便于应用。从抽取的结果来看,前1万次,前四阶矩值波动比较明显,超过1万次后均比较稳定,在1.5万次时趋于平稳,因此,考虑到计算时间与计算精度的平衡,把抽样次数设定为2万次。 (a)均值 (b)标准差 (c)偏度 (d)峰度图5 轨道板结构初始状态功能函数前四阶矩变化趋势 通过式(14)~式(17)以及蒙特卡洛有限元法确定的式(16)的前四阶矩均满足式(28),所以可利用式(25)、式(26)计算功能函数四阶矩可靠度指标及相应的失效概率,结果见表7。μG、σG、α3G、α4G的相对误差依次为0.080%、1.889%、5.785%和0.667%,3种退化工况下β4M的误差均为1.883%。 表7 轨道板结构初始状态功能函数前四阶矩及其可靠度指标 从表7可以看出,基于7点估计一维减维求解的功能函数前四阶矩与蒙特卡洛随机有限元法求解的前四阶矩较接近,误差最大的峰度值也在6%以内,可靠度结果大体接近,表明7点估计一维减维求矩的方法在减少计算次数的同时能够保持足够的精度。 用蒙特卡洛有限元方法验证了7点估计一维减维法求解轨道板结构初始状态功能函数(t=0)前四阶矩的正确性之后,对于某一时刻t(t=1,2,…,60),可以直接采取7点估计一维减维方法求Z(t)前四阶矩,分别代入式(25)、式(26)得到轨道板横向抗弯承载力在3种抗力衰减环境中的四阶矩可靠度指标,如图6所示。 图6 轨道板结构时变可靠度变化曲线 从图6可以看出,在抗力低速退化情况下,结构的可靠度指标变化较小;从结构投入使用的5.89下降到60年后的5.78,失效概率较小,可以认为结构在整个服役年限内,轨道板处于安全状态;在抗力中速退化情况下,结构可靠度指标的衰减较快,结构服役至57年时,可靠度指标低于目标可靠度4.2,说明由钢筋锈蚀导致的钢筋截面退化已发展,轨道板结构存在较大的安全隐患;在抗力严重退化的情况下,结构开始运营使用后,可靠度指标呈现急剧下降趋势,结构服役至35年时,可靠度已经低于规范要求,处于严重腐蚀环境中的轨道板结构受到外界恶劣环境的影响,再加上养护的不足,结构很快进入破坏阶段,需要加强维护与管理。 (1)本文建立了列车荷载与环境共同作用下CRTSⅡ型轨道板横向抗弯承载力的极限状态函数,并利用该函数发展了基于矩法的轨道板横向抗弯承载力时变可靠度分析方法,采用基于一维减维的点估计结合有限元方法计算极限状态函数的前四阶矩(均值、方差、偏度、峰度),采用四阶矩可靠度公式计算可靠度指标及失效概率。 (2)与蒙特卡洛方法对比分析表明,用7点估计一维减维的方法求解功能函数的前四阶矩,在大量减少计算次数的同时,能够保证计算结果的精度,此方法利于轨道结构可靠度分析与应用。 (3)算例假定轨道板处于3种不同侵蚀环境(低速退化、中等退化和严重退化)中,分析结果表明:轨道结构处于不同服役环境中时,其可靠度指标衰减程度有较大不同,在中等和严重退化的服役环境中需考虑加强轨道板横向抗弯承载力设计。

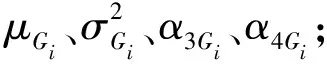
2.3 四阶矩可靠度指标及失效概率计算
3 算例

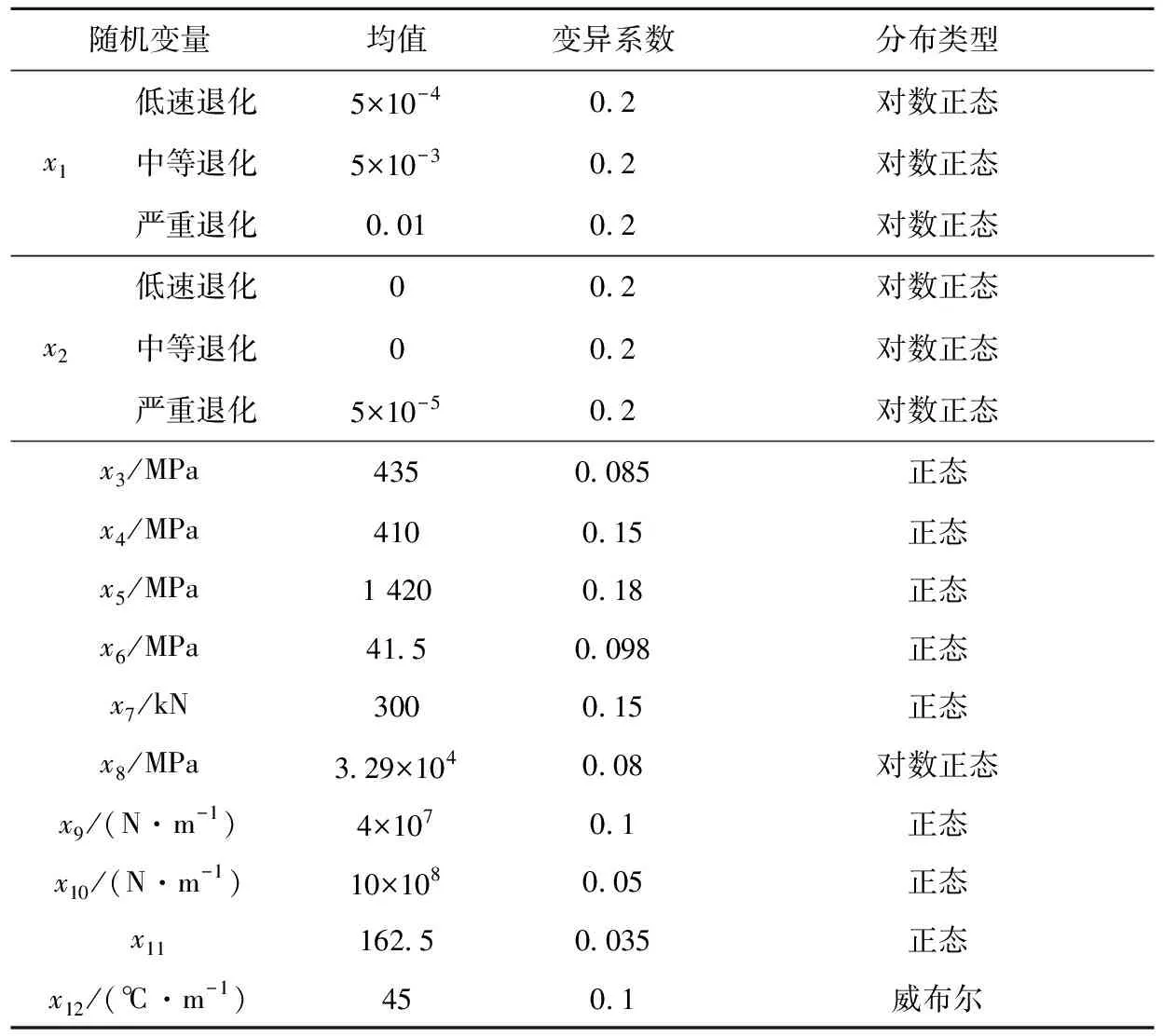
3.1 随机变量的7点逆正态转换值




3.2 轨道板结构初始状态可靠度计算




3.3 轨道板结构时变可靠度分析

4 结论

