带交易费用的欧式期权定价问题研究

丰月姣

(山西大同大学数学与统计学院,山西大同037009)

在期权续存期[0,T]内,如果没有有关风险资产的交易行为,则欧式看跌期权的价值满足方程

其中,r表示无风险收益率,σ表示风险资产的波动率,K表示欧式期权约定的交易价格。有关无交易费用的欧式期权定价研究已有许多文献。Chang和Shih[1]研究了CEV模型下的期权定价问题,通过二叉树模型方法得到了欧式期权定价的一个显式差分格式。之后,Xu和Knessl[2]采用Laplace变换得到了一个高精度的半离散差分格。稍后,Wong和Zhao[3]采用Laplace-Carson变换代替Laplace变换也得到了类似的结论。文献[4-5]则直接采用数值差分方法进行离散,虽然所得结论精度略有下降但是程序相对简单,具有较快的运算速度。

一个金融机构若在场外市场(OTC)出售给客户一份期权,那么它就面临风险管理问题。假定某金融机构出售了基于10万股某型号股票的欧式看跌期权,获利30万$。进一步假设

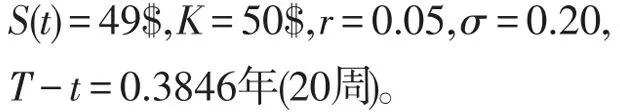
于是由Black-Scholes公式算的该期权的价值为24万$,金融机构以高出6000$的价值出售了这份期权。假设每次交易的费用比率为0.1%,则金融机构存在以下两种策略。

金融机构的第一种策略:

什么都不做,如果看跌期权不被执行,则该金融机构纯得收益30万$;但如果20周后,该类型股票的市场价为60$,则金融机构不得不以这个价格购买l0万股股票与该期权头寸对冲,花去交易费用6000$,然后再扣去期权费的收入,它将损失70.6万$。

金融机构的第二种策略:

在出售期权的同时,购买l0万股股票,该策略被称为抵补期权头寸策略,如果到期日该期权被执行,这个策略很有利:

如果在到期日T,股票价格下降至40$,此时看跌期权不会被执行,则在该股票头寸上将损失90万$,扣除期权费的收益,还亏60万$。

可以看出:在两种交易策略都出现不利情况时,第二种策略它比第一种策略少损失10.6万。通过第二种策略还可以看出构造投资组合除了获利以外,还可以有效的抵补期权金和交易费用的损失。

由此可见研究带有交易行为的期权定价问题更有现实意义。根据文献[6-10],如果在期权存续期内存在风险资产的对冲交易行为,根据LeLand模型的相关结果,期权价格公式满足

其中

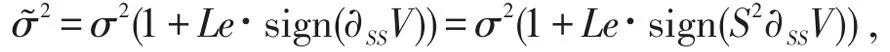
σ2表示风险资产自身的波动率,Le为LeLand系数满足

κ表示单位本金的风险资产交易的费用比率。δt表示交易频率,在投资策略二中δt=T。

由于增加交易费用之后,期权适合微分方程结构复杂,目前的研究重点在数值方法,有关期权的解析定价结果还未见文献。构造了一种新的误差分析方法,分析了近似结论的误差估计,结果表明:当波动率σ和σ2不满足Lipschitz条件和线性增长条件时,上述文献中的误差估计结论依然成立。

1 单参数摄动方法

为了方便证明,我们同时定义如下的符号

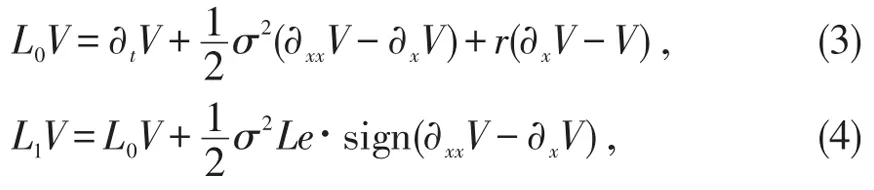
若不存在交易费用,即κ=0时,L1V=L0V,作变换

则欧式看跌期权适合的抛物方程问题(1)转化

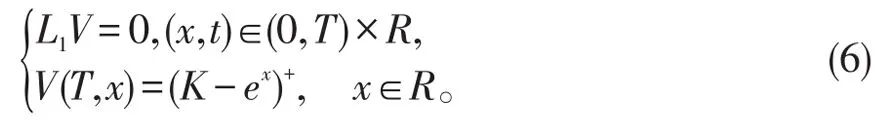
下面采用扰动理论中单参数摄动展开的方法去处理抛物问题(7)。假定V(t,x)在ε=0附近可以展成幂级数

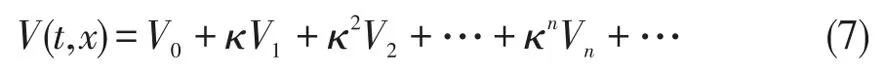
从而将公式(7)和公式(2)代入抛物问题(6)并按照ε幂的次数进行归类,可得

再由x和t的任意性,令κ的相同次幂的系数为零,得

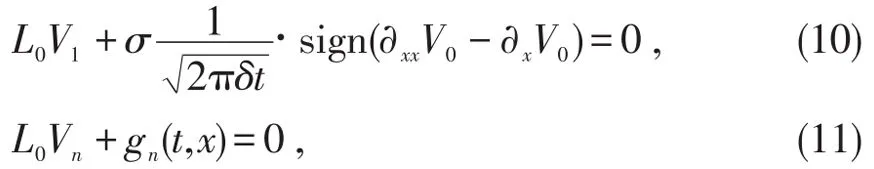
其中

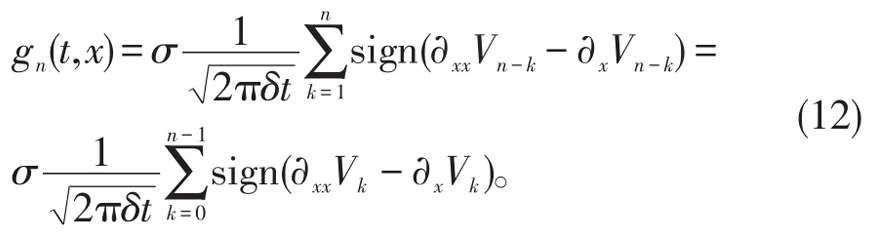
进一步,根据公式(8),将抛物方程(6)中初边值条件进行分解

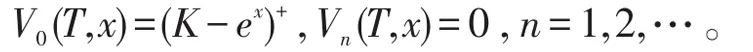
至此,抛物型方程(7)的求解问题转化为一系列常系数抛物方程初边值问题,其中V0(t,x)是抛物初边值问题

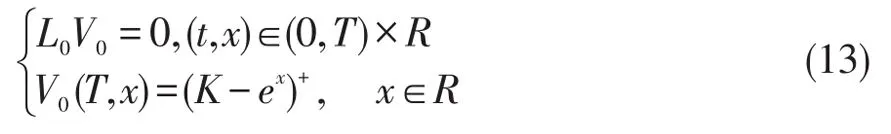
的解,Vn(t,x)为如下偏微分方程初边值的解

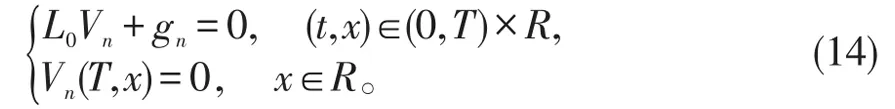
由文献[10]可知,V0(t,x)是经典Black-Scholes模型下的欧式期权的解,则它可表示为

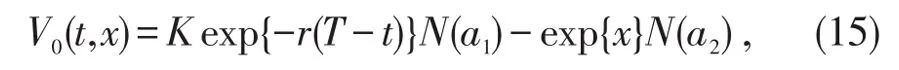
其中

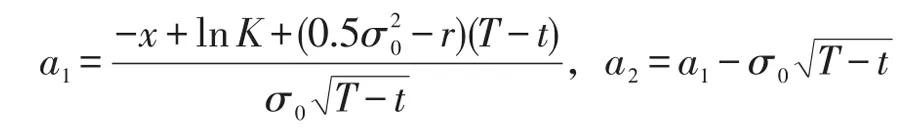
下面考察Vn(t,x)。注意gn(t,x)仅与∂xxVk-∂xVk有关,而与 ∂xxVn-∂xVn无关(k=0,1,…,n-1),这启发我们采用递推法完成如下结论的证明。

引理1常系数抛物初边值问题(14)的解可表示为

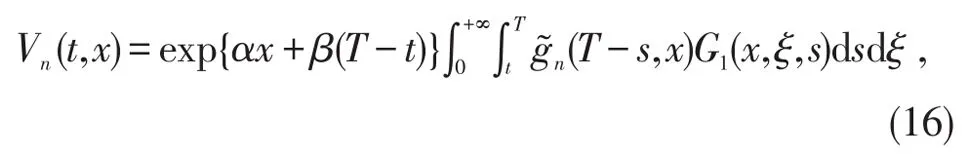
其中

证明作变换

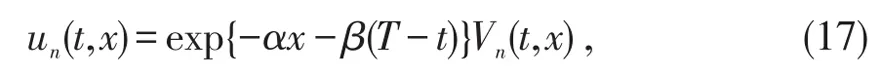
同时令τ=T-t,则抛物方程(14)可以转化为

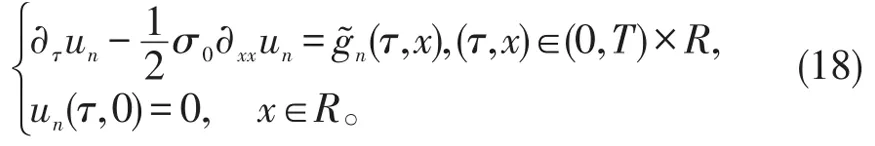
注意到gn(t,x)和g͂n(τ,x)是解析的,根据文献[8],抛物问题(18)的解可表示为

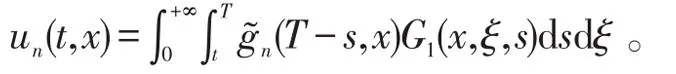
对变换(17)进行逆变换即可完成定理证明。

证毕。

综合引理1和公式(15),有如下结论成立。

定理1欧式看跌期权的定价公式P(t,S)有如下形式的近似解析式

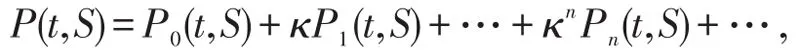
其中

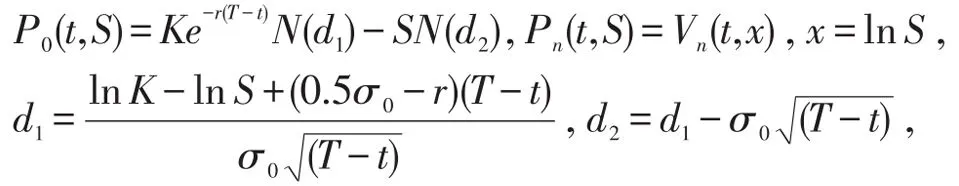
其它各量见引理1。

同理可证欧式看跌期权定价公式,这里只给出上升敲出看涨期权的结论。由文献[10]可知,上升敲出看涨期权的价格C(t,S)满足如下抛出初边值问题

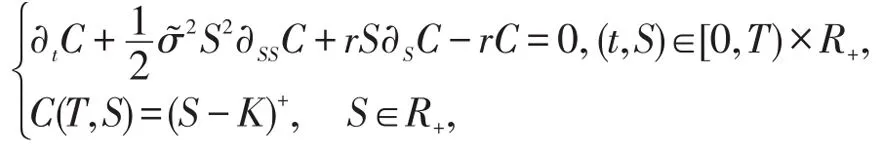
类推上述证明,可得上升敲出看涨期权的近似定价结论。

定理2若C(t,S)表示上升敲出看涨期权的价格,则它可以表示为

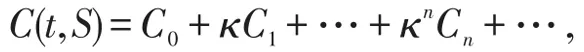
其中

α,β和G(x,ξ,t)见引理1;d1和d2见定理1。

2 误差估计

在以后的误差分析中需要一些辅助结论,由文献[10],容易得到

其中n(∙)为标准正态分布的密度函数。

定理3存在不依赖x和t的正常数M,使得|P(t,S)-P0(t,S)|≤Mε。

证明考虑P(t,S)和V(t,x)的对应关系,这里只需证明

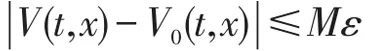
成立。令x=lnS-lnB,E0(t,x)=V0(t,x)-V(t,x),显然

又因为LεV(t,x)=0,所以由公式(5),可得

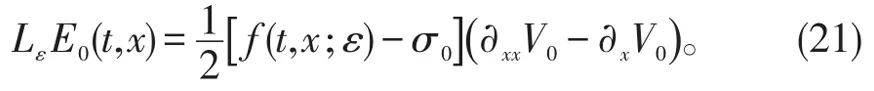
故联立公式(20)和公式(21),E0(t,x)为抛物初边值问题

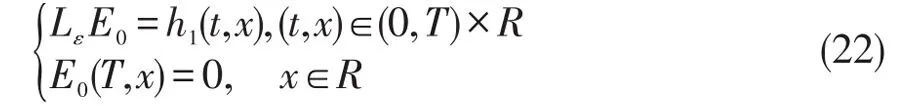
的解,其中

由Feynman-Kac公式可知[12],抛物初边值问题(22)的解可以表示为如下概率形式

其中exp{-r(T-t)}Xt是一个L∞鞅。注意n(d1)≤(2π)-0.5,从而

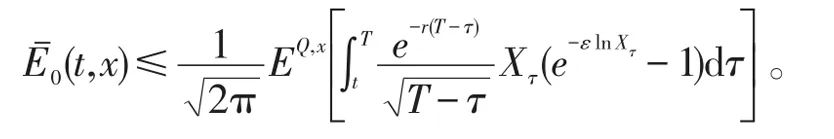
利用引理1,我们有

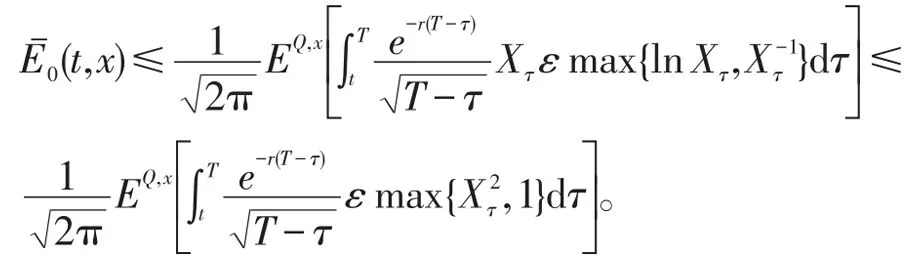
考虑到exp{-r(T-t)}Xt是鞅,易见| |Xt是下鞅,从而由Doob不等式,可得

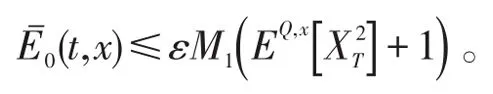
证毕。

定理4一致收敛到P(t,S),即P(t,S)对任意的正整数n存在不依赖n,x和t的正常数M使得

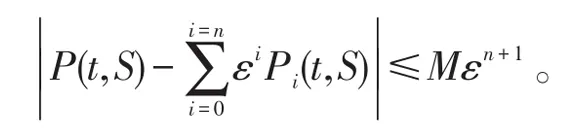
证明类似定理3,这里只证明

|En(t,x)|≤Mεn+1。

其中

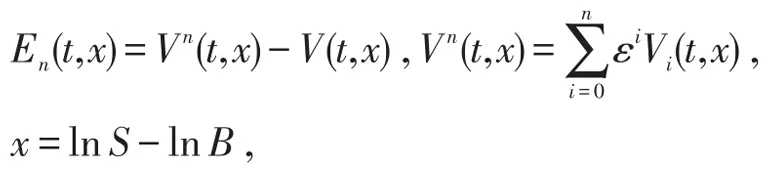
容易证明En(t,x)满足初边值条件En(t,0)=0,En(T,x)=0,并且

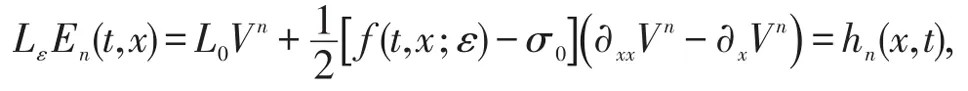
其中

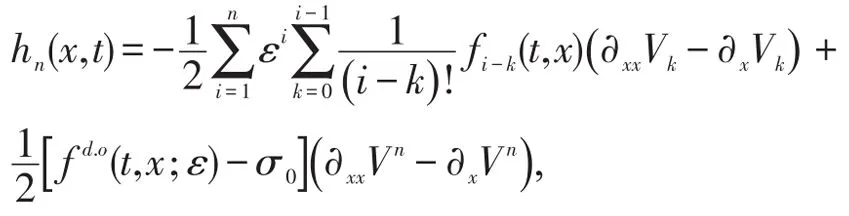
从而En(t,x)为抛物初边值问题

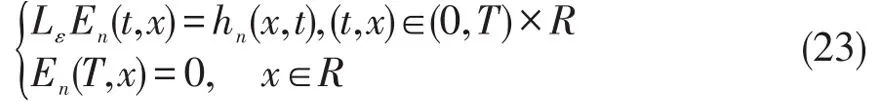
的解。首先,类推文献[7]之推导过程,hn(x,t)还可以写成

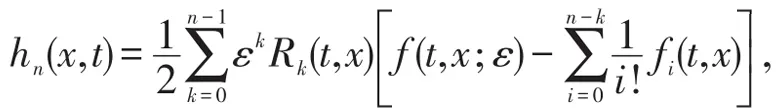
其次,利用公式(19),可得对任意的(t,x)∈[0,T]×R有

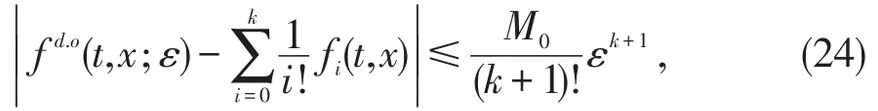
再次,由Feynman-Kac公式可知[11],抛物问题(23)的解可表示为如下形式的概率问题

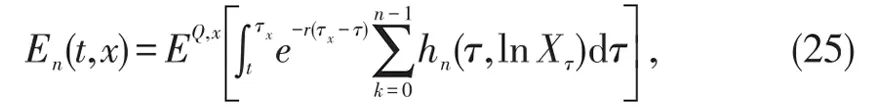
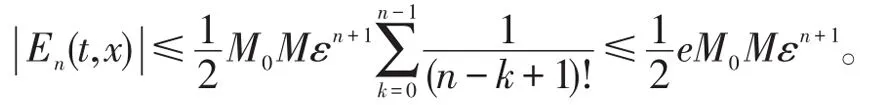
证毕。