在轨加注任务中变质量特性下的空间操作臂状态扩展自适应镇定控制

秦利，闫莉莉，刘福才,*，梁波

1. 燕山大学 电气工程学院，秦皇岛 066004 2. 燕山大学 材料科学与工程学院，秦皇岛 066004

在轨加注能延长卫星寿命，减小运载器规模，世界各国均进行了相关技术研究，如美国“轨道快车”计划、德国OLEV (Orbit Life Extension Vehicle)项目、俄罗斯进步号飞船向空间站传输液态推进剂、中国对天宫二号的在轨燃料补给等[1-2]。最初的在轨加注主要通过推进剂直接传输实现补给，如美国“Restore-L”航天器[3]通过操作臂捕获目标并完成结构连接和推进剂传输接口连接进行燃料直接注入。欧空局ASSIST项目[4]通过操作臂辅助探针-锥孔连接机构完成对接锁紧和接口连接，进行流体燃料传输。随着在轨服务平台与有效载荷设计逐渐趋于更便于组装拆卸的模块化形式，在轨加注出现了通过推进剂贮箱更换，如设想收集在轨废弃航天器燃料给需要卫星加注的Hermes计划[5]，以及直接将整个推进系统模块进行更换的推进剂补给方式，如航天器通过机械臂与自由飞行的哥伦布平台对接并置换推进舱[6]。美国轨道延寿器[7]在捕获目标航天器完成对接后可作为组合体的推进单元进行轨道与姿态控制。其中，空间操作臂要完成服务航天器与目标航天器的交互对接、推进剂传输接口连接、推进模块更换等关键操作[8-10]，复杂而精细的操作任务对其控制精度和性能提出了更高的要求。

空间待加注在轨服役卫星种类多数量大，所配备的推进剂模块也不尽相同。加注任务中，自由飞行操作臂捕获目标航天器实现结构连接，并将目标航天器上旧推进剂模块拆除，替换成服务航天器携带的新增模块，空间操作臂负载涉及的种类不同，惯性参数变化范围较大。服务航天器与目标航天器成功对接后，其组合整星成为在轨加注过程中的空间操作臂系统的载体，整星基座质量特性的变化使其与空间操作臂系统间的动力学耦合作用发生变化；推进剂模块更换后，新增推进剂模块和被替换推进剂模块分别集成于目标航天器和服务航天器上，两航天器分离后本体质量特性改变，对各自配备的空间操作臂系统的动量扰动随之改变。可见，这类任务存在复杂的质量特性变化问题。类似问题在现有研究中，有从参数预测角度对质量特性进行试验测量或在线辨识的研究[11-12]。还有通过设计更有效的控制策略，保证系统稳定性的研究。如文献[13]考虑燃料消耗的影响，设计系绳拉力和推力器协调控制方法实现对抓捕后复合体的姿控。文献[14-15]分别设计了基于特征模型的自适应控制方法、基于自适应神经网络的鲁棒控制方法对参数不确定机械臂系统运动状态进行控制。文献[16]针对存在参数不确定和外界干扰的柔性机械臂轨迹跟踪问题，设计基于T-S模糊模型的滑模鲁棒控制方案和双柔性振动并行控制方案。同样，对于复杂多变的非结构化在轨加注操作，在控制器研发时，考虑系统中本体与空间操作臂间的动量耦合，及操作对象的不确定性对系统运动状态的影响，是十分必要的。

服役于太空微重力环境的空间机构，其控制器研发和性能验证是在地面完成的，因此，伴随着航天工程的发展，人们同步研发了多种微重力环境模拟试验方法，但复杂对象与过程的地面任务级微重力模拟试验平台仍难以有效搭建。如MFD (Manipulator Flight Demonstration)和SFA (Small Fine Arm)的工程试验数据分别给出了末端定位误差[17]与关节驱动力矩[18]在微重力条件下与地面悬吊模拟试验中的对比结果，并推测其差异是由地面模拟环境无法产生真实微重力效应引起的。重力释放后，系统运动行为受微小力/力矩的影响不可忽略[19]，而地面研发时往往容易将其掩盖，令在轨动力学特性和控制性能存在不可预测性，或造成速度抖振、部件卡滞及控制失灵等在轨故障，如航天器在液体燃料耗散和柔性附件扭转振动作用下动力学特性发生变化[20]，本体与操作臂间的动量扰动随之变化。重力梯度摄动力矩扰动下偏心率较大时，机械臂出现混沌等非线性特征，系统可能失稳发生翻滚运动[21]。文献[22]设计了神经网络分块滑模自适应控制方案对捕获后的空间机器人混合体姿态、关节受扰运动状态进行镇定。在轨加注任务面向非结构化的操作对象，涉及航天器对接、推进剂模块更换等多个操作过程，研发时难以实现全周期的、遍历性的模拟验证，针对装调时可能引起或掩盖的非线性动力学特性，所设计的控制器若能适应实际多变的操作任务中变化的控制对象及环境，将很大程度提高控制系统的有效性和可靠性。

基于上述考虑，本文关注了如何设计控制器，能在非服役力学环境调试后，空间应用同样有效的问题，参照从地面模拟试验到空间应用操作的控制器研发过程，分析在轨服务航天器辅助操作臂在加注过程中载体与负载变化时的系统非线性动力学响应。为消除整个研发周期中，重力环境变化及其与质量特性变化的耦合对控制器设计与调试的影响，建立质量特性改变时不同重力环境下操作臂统一模型，基于重力加速度g的自适应律设计，扩展系统状态，在系统内部实现对力学环境变化的估计，实现系统具有耗散结构的Hamilton形式，基于能量函数整形方法设计预置镇定控制项，实现对质量特性变化引起的系统非线性的控制。提出一种适用于变化的控制对象及环境，在不改变控制器结构和参数的情况下可实现操作臂系统混沌运动自适应抑制和精确末端定位的状态扩展自适应镇定控制方案。

1 系统动力学模型

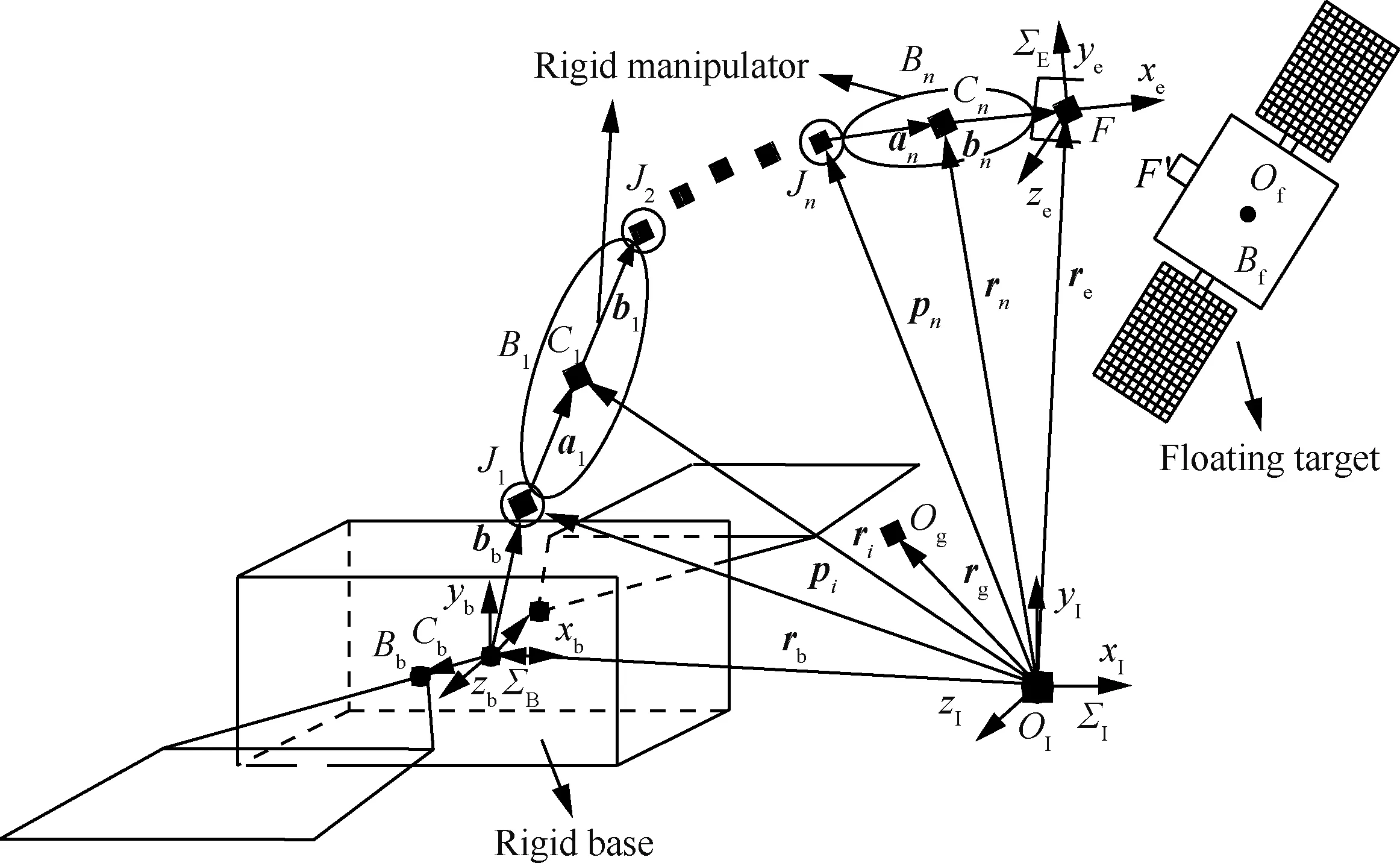
图1 n自由度空间机器人模型Fig.1 Model of n-DOF space robot

本文所研究的n自由度在轨加注辅助空间机器人系统由载体、操作臂和末端执行器组成，如图1 所示。建立的坐标系如下：(1)坐标系∑I-{xI,yI,zI}为惯性坐标系；(2)坐标系∑B-{xb,yb,zb}为基座坐标系；(3)坐标系∑E-{xe,ye,ze}为末端坐标系。定义如下符号：Bb表示基座空间站；Bf表示自由漂浮目标航天器；Bi(i=1,2,…,n)表示第i个连杆；Ji为连接Bi和Bi-1的关节；Ci为Bi的质心;OI为惯性原点；Og为整个空间机器人系统的质心；Of为目标物体的质心；ai为Ji指向Ci的位置矢量；bi为Ci指向Ji+1的位置矢量；ri为惯性原点OI指向Ci的位置矢量；rb为惯性原点OI指向Cb的位置矢量；re为惯性原点OI指向末端执行器的位置矢量；rg为Og在惯性坐标系下的位置矢量。pi为Ji在惯性坐标系下的位置矢量；F和F′分别为末端和目标航天器上的接触捕获点。

根据拉格朗日方程和动量守恒原理，建立空间操作臂系统动力学方程为

(1)

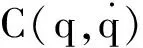
将受到操作臂载体惯性参数变化、负载不确定及重力释放耦合影响的部分与标称项分离，式(1) 可写为

(2)

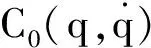
地面研发阶段，系统处于重力环境，则

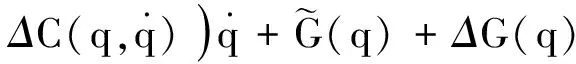
(3)

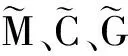
空间在轨加注阶段，若航天器本体浮动，会造成对操作臂的动量扰动，动力学模型中

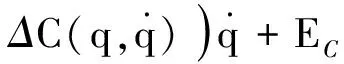
(4)

若某种惯性参数下令载体浮动较小，或完成空间站上机构的在轨加注任务时，载体质量远大于操作臂质量时，广义雅可比矩阵与固定操作臂雅克比近似，可忽略基座的动量干扰，等价为固定基座模型，此时

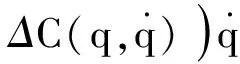
(5)

2 非线性动力学特性分析

基于上述模型，考虑地面研发的过程，先以常规控制器为例，调试合理的控制器参数。参照前述在轨加注操作过程，对更换新旧推进剂模块和对接不同类型航天器过程中，负载质量特性与基座动量耦合作用的变化对系统末端精度的影响进行分析，并探讨引起这种现象的系统动力学特性。同时，考虑航天器与推进剂模块种类繁多、组合多变，研究操作不同种类推进剂模块、对接不同类型航天器时，系统质量特性变化对非线性动力学响应的影响。

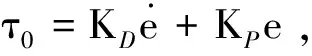
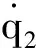
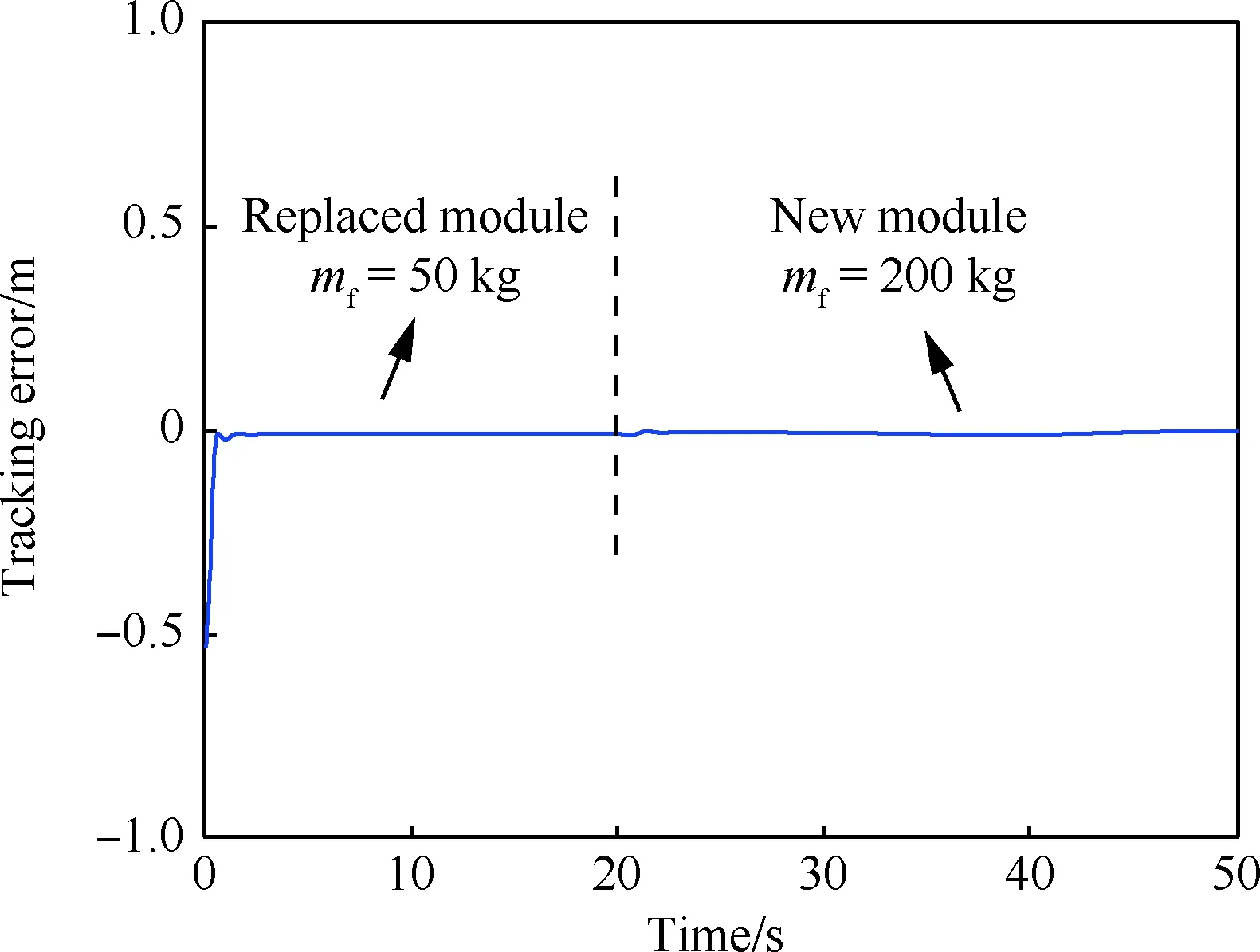
图2 地面阶段推进剂模块更换过程仿真结果Fig.2 Results of simulation of process of propellant module replacement on ground stage

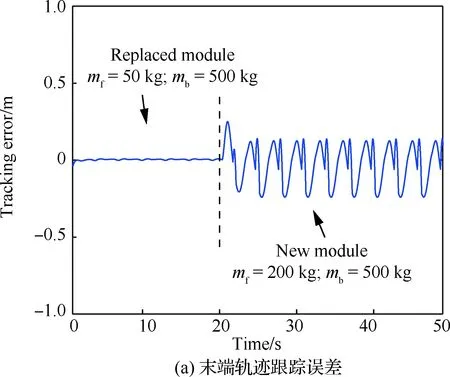
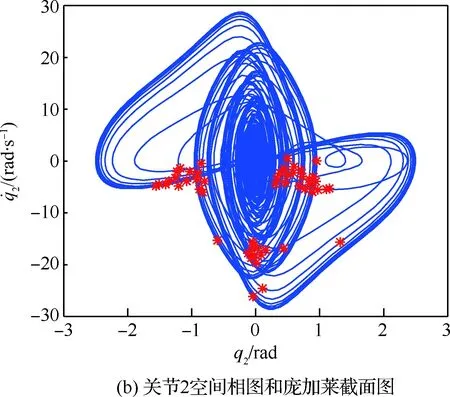
图3 推进剂模块更换过程中漂浮基操作臂仿真结果(mf=200 kg,mb=500 kg)Fig.3 Results of simulation of free-floating manipulator in process of propellant module replacement (mf=200 kg,mb=500 kg)

由图2～图6中前20 s仿真结果表明，不同工况下操作臂跟踪误差一定时间内均趋于0。20 s时，所选仿真参数模拟了某种操作臂负载和基座质量随任务发生变化的情况，图2显示地面调试时控制效果仍能满足控制要求，图3～图6显示空间应用阶段操作臂末端误差曲线突变明显，无特定规律，对应的关节空间相图、庞加莱截面图说明系统内部出现了不同程度的混沌运动。

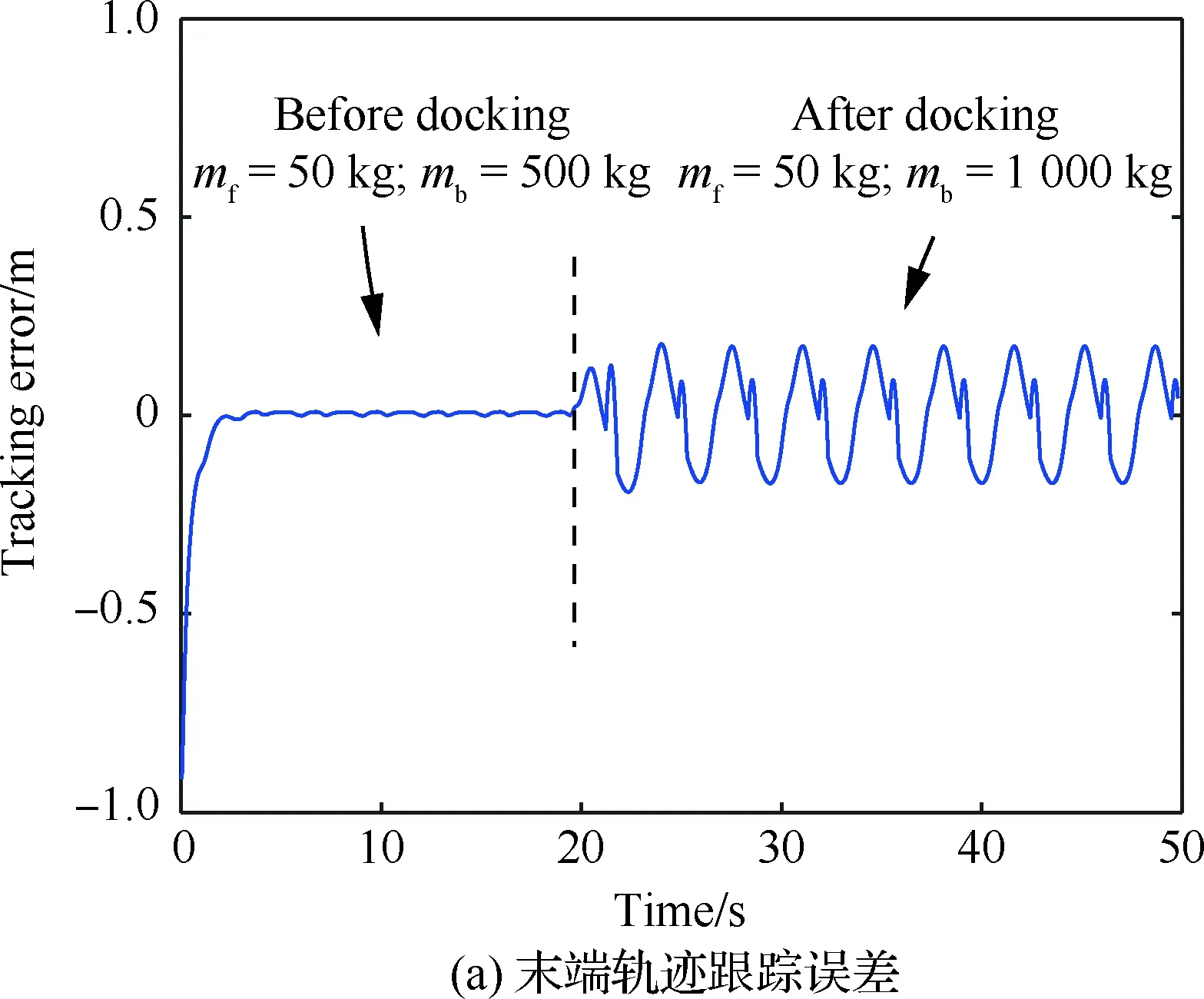
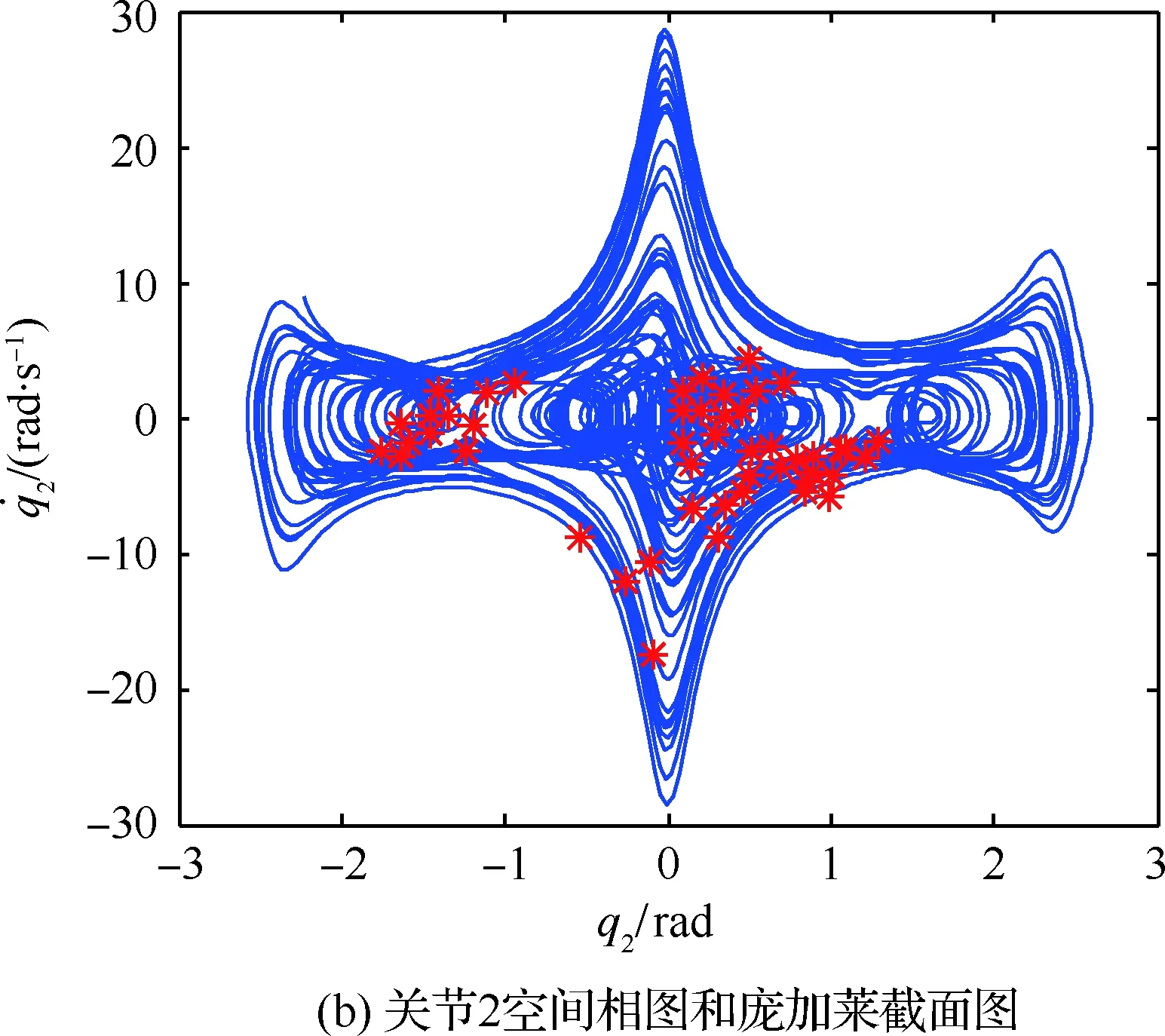
图4 捕获对接过程中漂浮基操作臂仿真结果(mf=50 kg,mb=1 000 kg)Fig.4 Results of simulation of free-floating manipulator in process of capturing and docking (mf=50 kg,mb=1 000 kg)

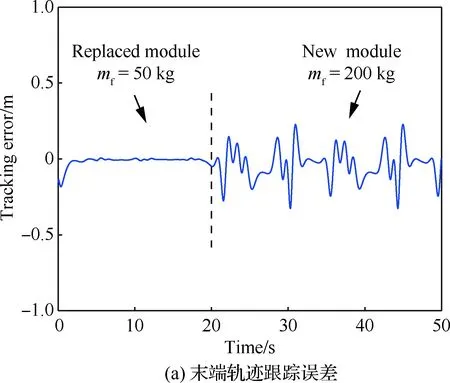
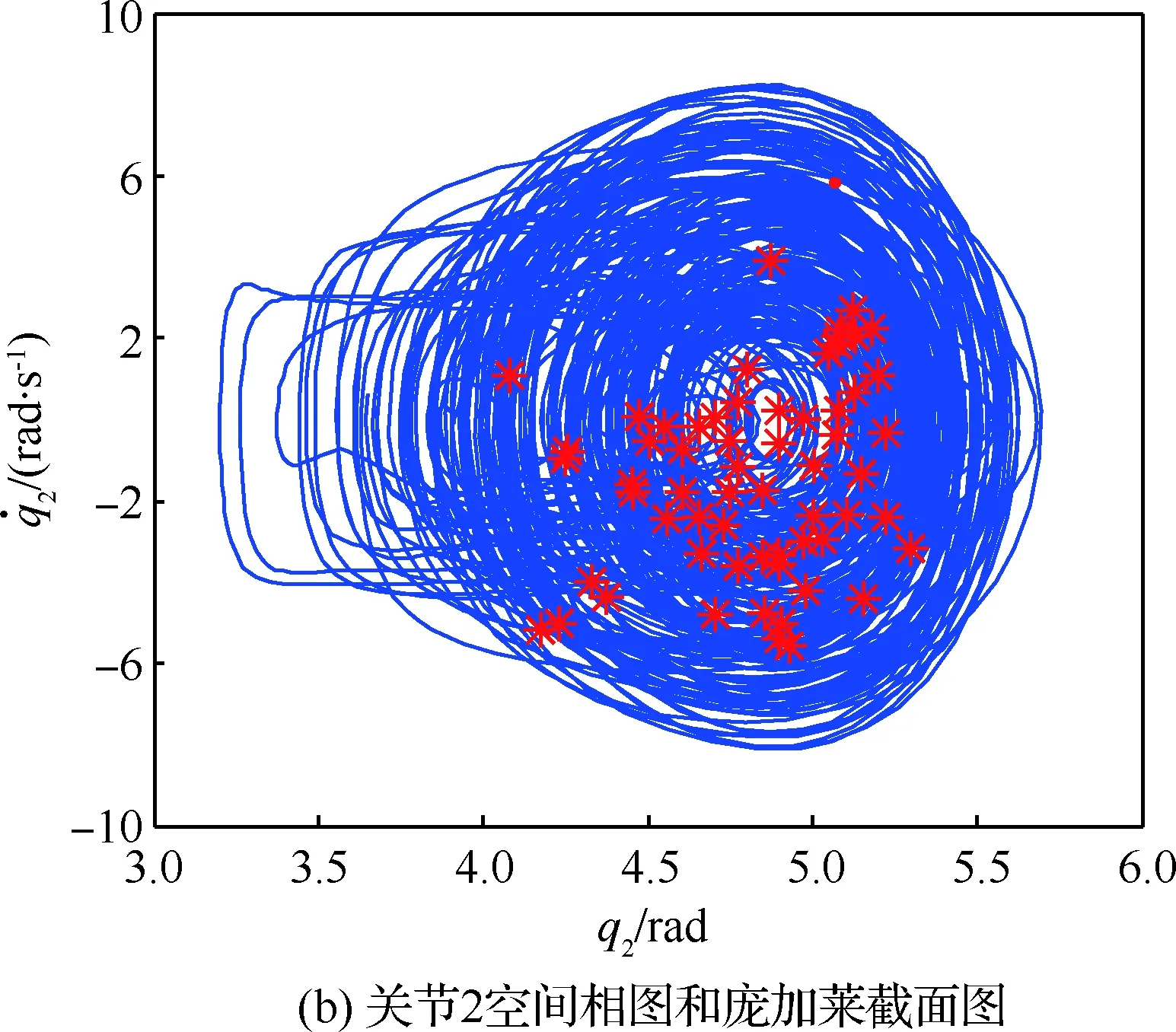
图5 推进剂模块更换过程中等价固定基操作臂仿真结果(mf=200 kg)Fig.5 Results of simulation of space fixed-base manipulator in process of propellant module replacement (mf=200 kg)

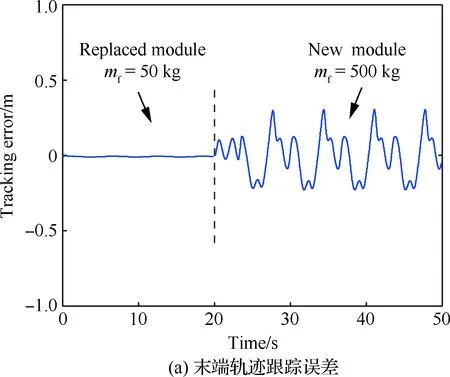
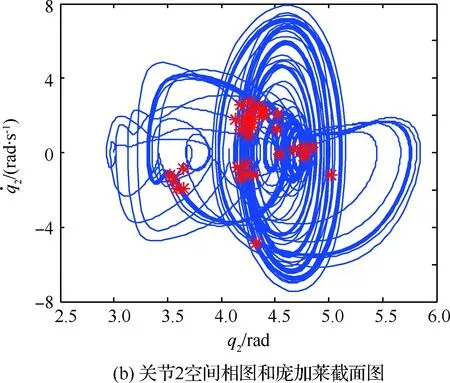
图6 推进剂模块更换过程中等价固定基操作臂仿真结果(mf=500 kg)Fig.6 Results of simulation results of space fixed base manipulator in process of propellant module replacement (mf=500 kg)

进一步分析负载及基座质量参数特性变化对系统非线性动力学响应的影响。图7～图9分别为空间漂浮基和空间固定基座操作臂系统基座和负载质量特性变化时对应的分叉图，表明不同基座和负载质量特性下系统发生非线性混沌运动的参数范围。可以看出，在所给参数下，所操作的模块质量或对接后的基座质量处于某些范围时，对应截面为分散的点，表明系统出现不同程度的混沌运动。充分说明在轨加注过程中负载和基座参数组合变化可能引起的系统非线性动力学响应。

综上所述，空间操作臂在轨加注时，系统质量特性的变化可能会使空间操作臂在一定范围内出现混沌运动，对系统稳定运行造成影响。这些仿真结果，从一定角度解释了在实际工程中，地面调试效果良好的操作臂应用到太空时却出现强烈抖震、卡死、失控等任务失败的情况。

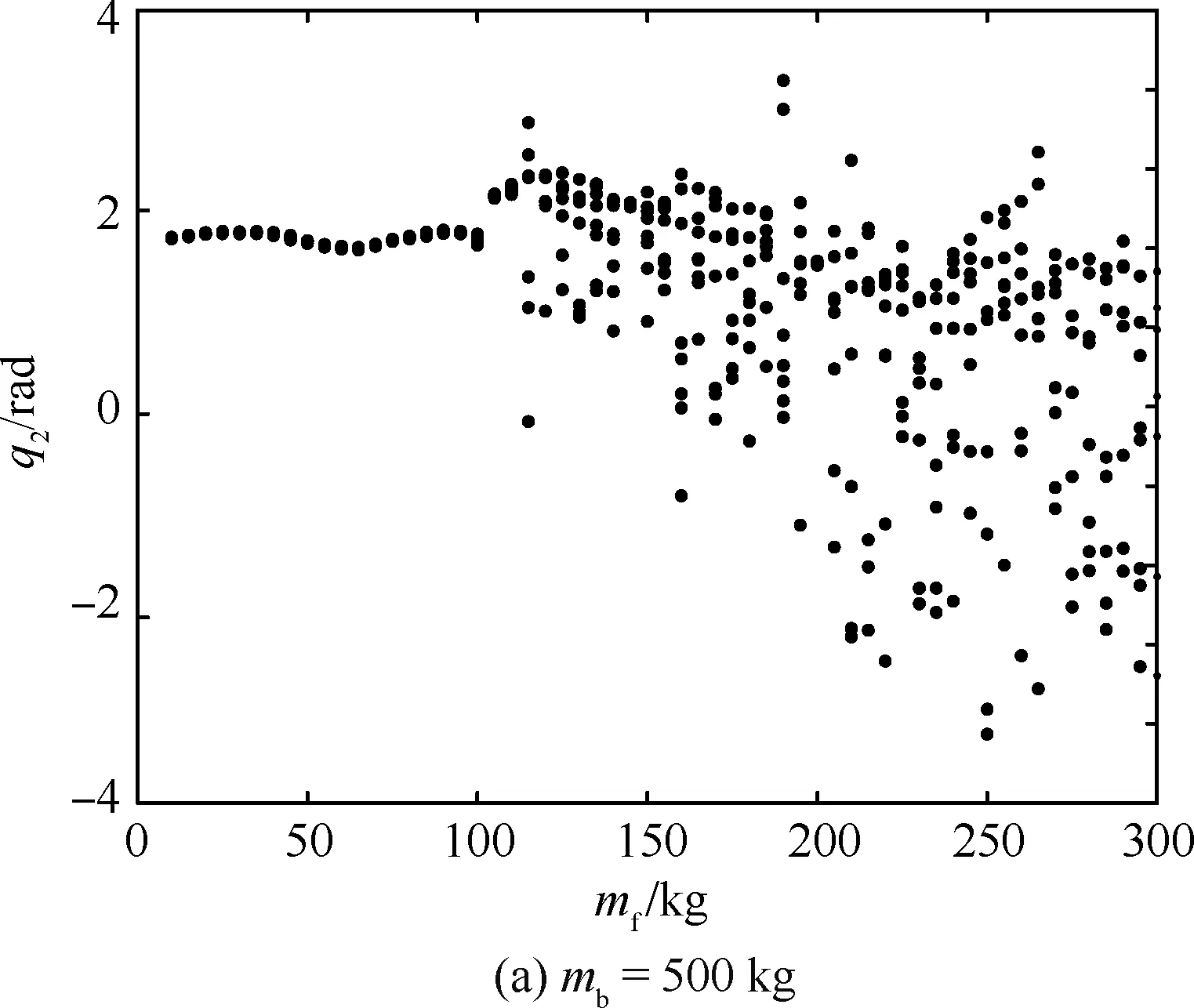
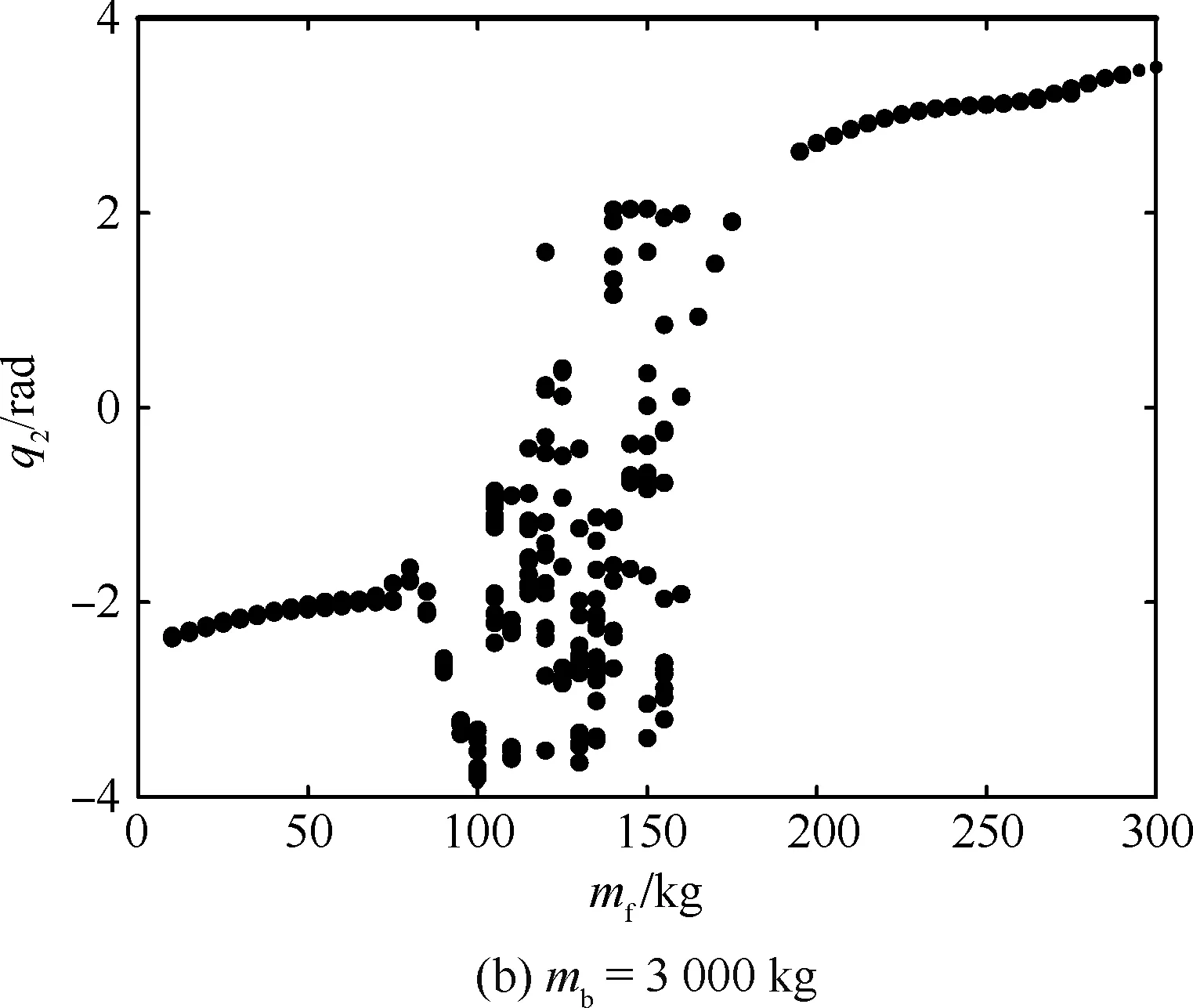
图7 操作不同模块时漂浮基机械臂关节2分叉图Fig.7 Bifurcation plot of Joint 2 when free-floating manipulator operates different modules

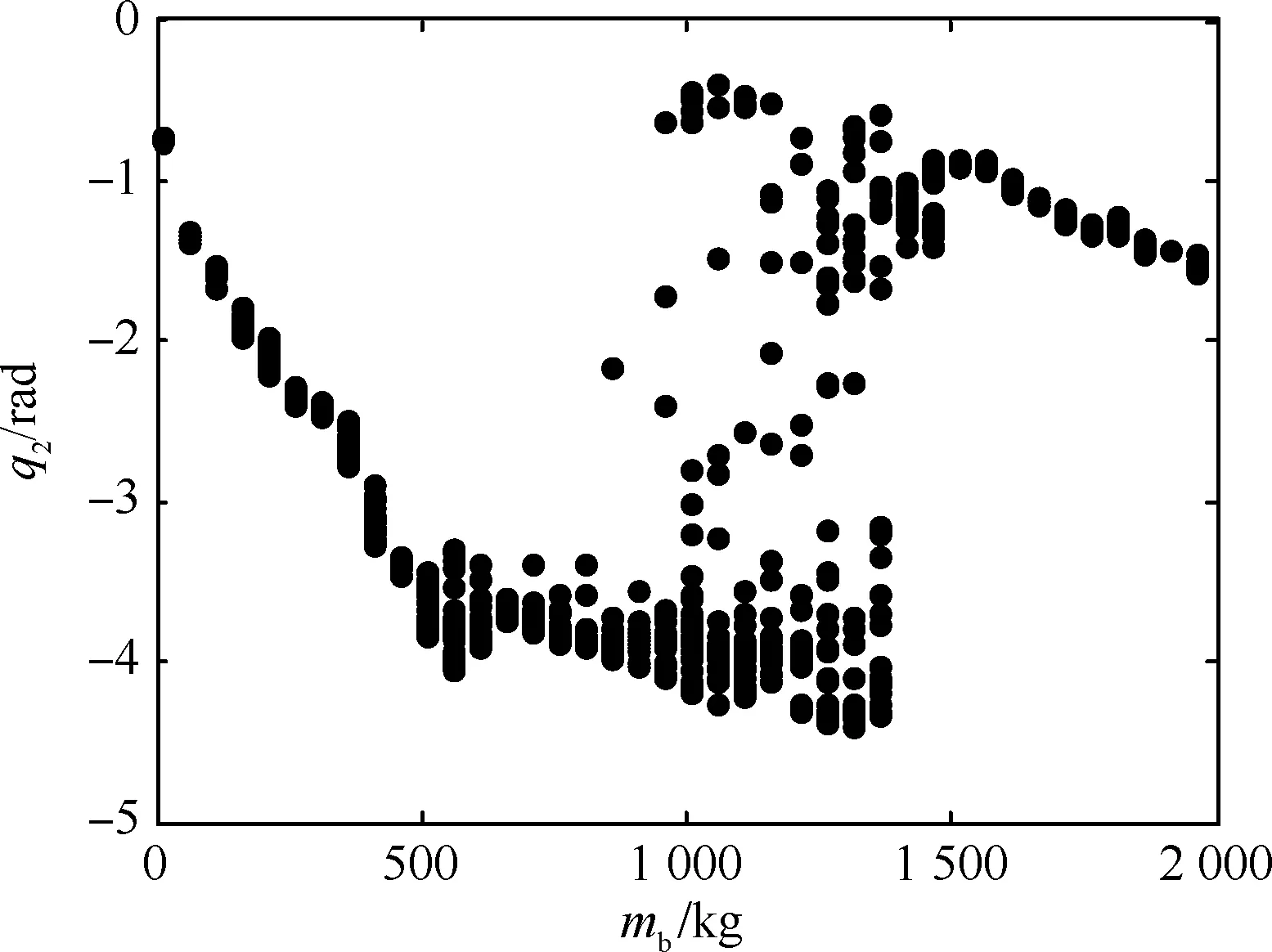
图8 对接不同航天器时漂浮基机械臂关节2分叉图(mf=50 kg)Fig.8 Bifurcation plot of Joint 2 when free-floating manipulator docks different spacecraft (mf=50 kg)

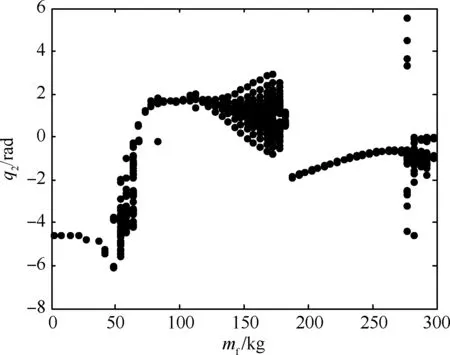
图9 操作不同模块时等价固定基操作臂关节2分叉图Fig.9 Bifurcation plot of Joint 2 when fixed-base manipulator operates different modules

3 状态扩展自适应镇定控制器设计

基于以上分析，相比参数复杂的控制律，为减少系统内在随机性的引入，且便于在实际空间工程实现，考虑从能量角度设计结构简单的控制器，使闭环系统形成具有耗散结构的广义Hamilton形式[24]，进而通过所设计驱动力在体系内进行非线性相互作用时产生的有效能量交换，令系统具有一定的自组织能力，实现非平衡状态下无序运动向有序演化的可能性。

在系统的Hamilton实现中，考虑系统内部对势能随力学环境变化的自适应性，设计g的估计误差为扩展状态变量，使控制器能自适应从调试阶段到服役阶段力学环境的变化，从而在地面调试中获取更有效的控制参数，在一定程度上将降低前述问题对系统运动状态和控制性能的影响。

3.1 状态扩展Hamilton模型

将重力加速度g看做系统的一个变量，设θ=g，则可写出地面调试和空间应用不同阶段操作臂动力学方程的统一形式为

(6)

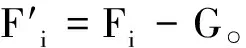
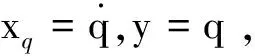
(7)

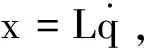
(8)

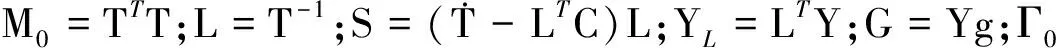
Hamilton函数描述了系统具有的总能量，针对该系统可表示为系统动能与势能之和，参考广义Hamilton系统中虚拟势能的定义[26]，选取Hamilton函数为

(9)

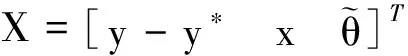
对Hamilton函数求偏导，整理可得如下形式

(10)

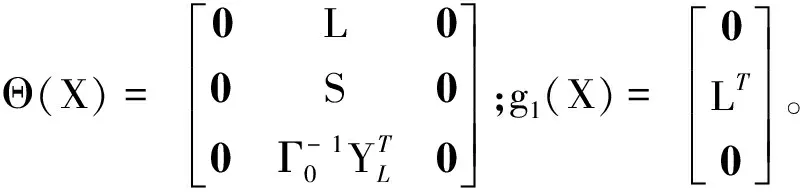
3.2 控制问题形成

针对第2节所述空间操作臂系统存在的非线性动力学响应，本文的控制问题可描述为：系统一旦进入混沌状态，可通过控制力矩将状态变量渐进趋于期望的平衡状态，并脱离混沌状态，且自适应于地面和空间两种环境。

考虑系统存在一些外界干扰，系统Hamilton模型可描述为

(11)

式中：ω为系统参数变化及外部干扰造成的系统扰动项。

系统式(6)的控制问题可进一步表述为设计状态反馈控制器u，使得相应闭环系统满足：

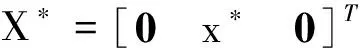
2) 当ω≠0时，对于给定的γ>0，系统具有L2干扰抑制特性，且满足一定的性能指标，即

(12)

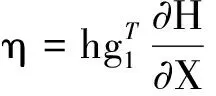
3.3 控制策略设计及稳定性证明

为了使系统能量函数的极小点是期望的平衡点，利用Hamilton模型的能量耗散特性对能量函数进行整形[27]，设计预置镇定控制项为

(13)

式中：kp为正定对角系数矩阵。

将式(8)所示状态方程整理为

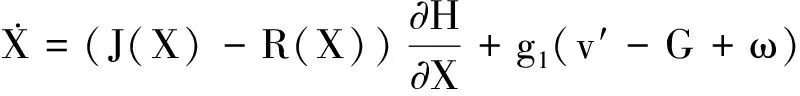
(14)

式中：ν′=u-ν0；J(X)和R(X)分别为互联矩阵和阻尼矩阵。

设计自适应项和鲁棒项分别如式(15)和式(16) 所示，即

(15)

(16)

式中：Ψ=YT；I表示单位矩阵。

令ν′=νG+νr，则系统的输入控制量为

u(X)=ν0(X)+ν′(X)

(17)

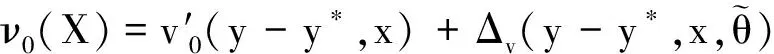
(18)

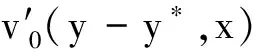
(19)

选取李亚普诺夫函数：

V(X)=H(X)

(20)

李亚普诺夫函数的微分形式为

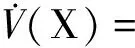
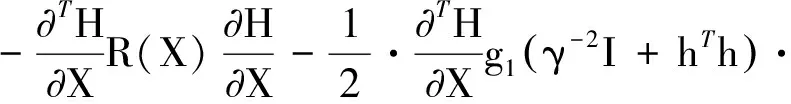
(21)

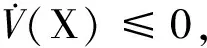
当ω≠0时，将式(21)重写为

(22)

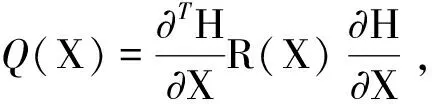
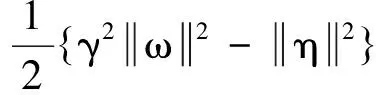
(23)

式(23)为该Hamilton系统的耗散形式，同时V(X)=H(X)具有正定性，Q(X)具有半正定性。可见，系统满足无源性条件，并对外部干扰具有干扰抑制特性，控制问题式(2)得证。

4 仿真验证

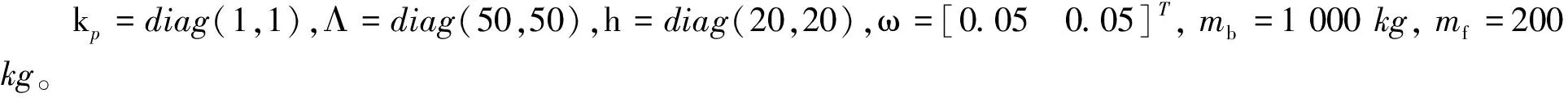
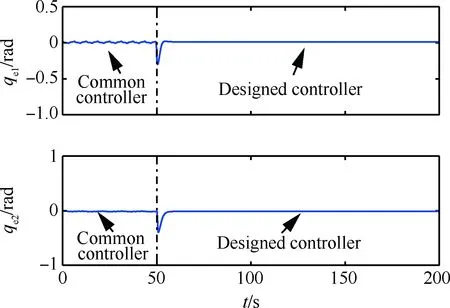
图10 地面调试阶段仿真结果(mf=200 kg)Fig.10 Simulation results in ground debugging stage (mf=200 kg)

图11 推进剂模块更换过程中漂浮基操作臂仿真结果(mf=200 kg,mb=500 kg)Fig.11 Results of simulation of free-floating manipulator in process of propellant module replacement (mf=200 kg,mb=500 kg)

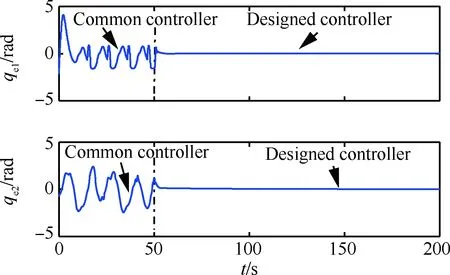
图12 捕获对接过程中漂浮基操作臂仿真结果(mf=50 kg,mb=1 000 kg)Fig.12 Results of simulation of free-floating manipulator in process of capturing and docking (mf=50 kg,mb=1 000 kg)

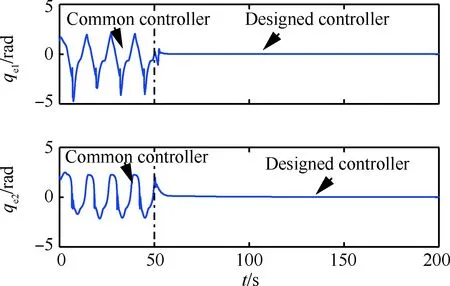
图13 推进剂模块更换过程中等价固定基操作臂仿真结果(mf=200 kg)Fig.13 Simulation results of space fixed base manipulator in the process of propellant module replacement(mf=200 kg)

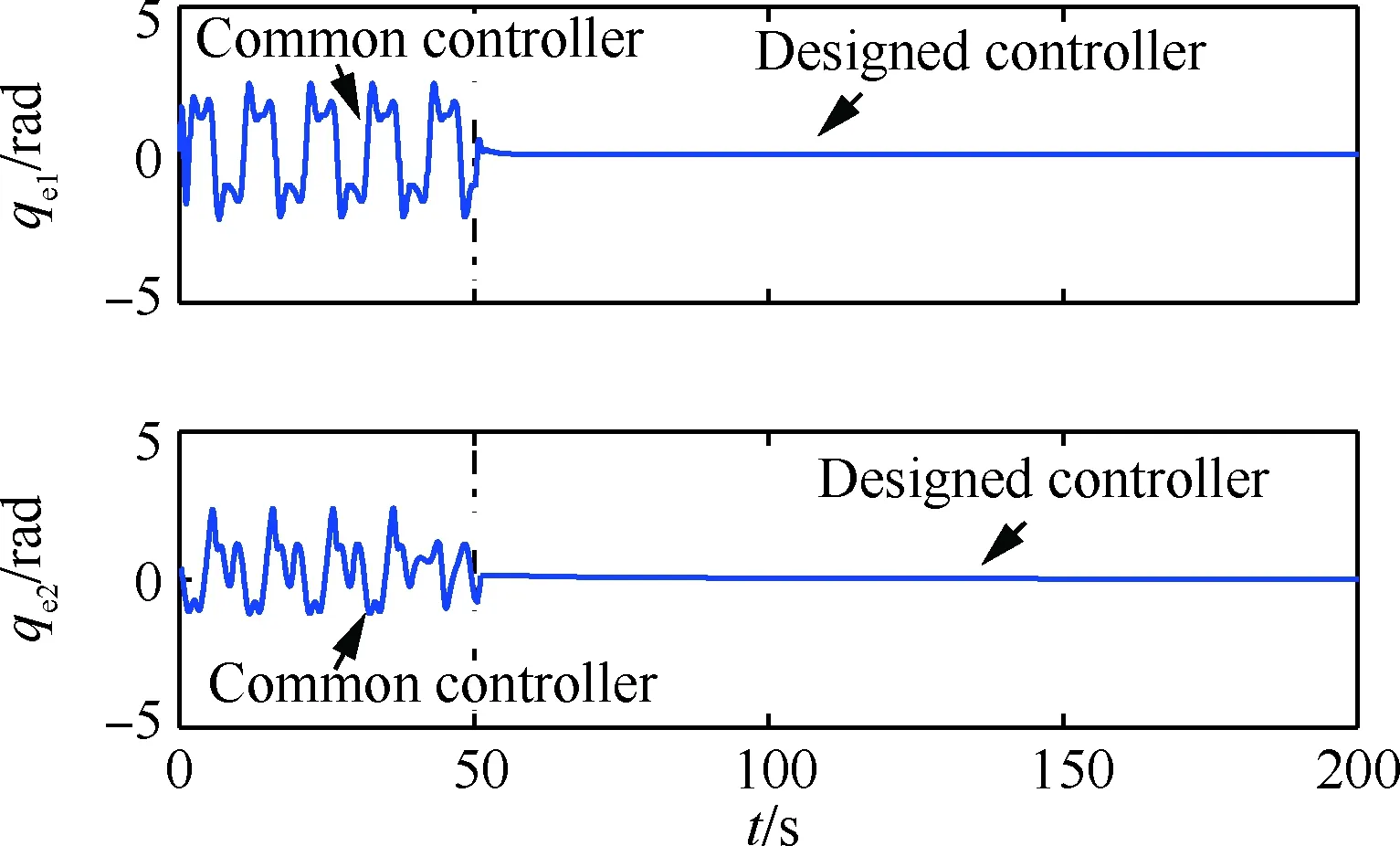
图14 推进剂模块更换过程中等价固定基操作臂仿真结果(mf=500 kg)Fig.14 Results of simulation of space fixed base manipulator in process of propellant module replacement (mf=500 kg)

如图10～图14所示，地面环境下，采用常规控制器进行控制时，无混沌现象，切换成所设计控制器后仍能实现较好的控制效果。微重力环境下，前50 s在常规控制器下出现混沌运动，切换成所设计控制器之后，混沌运动得到抑制，关节轨迹跟踪误差趋近于0 rad。图15为不同重力环境下重力加速度g的估计曲线，可见，所设计自适应律能在地面环境下快速估计出其值为9.8 m/s2，在空间环境下其值为0 m/s2。仿真结果验证了所设计控制器的有效性。

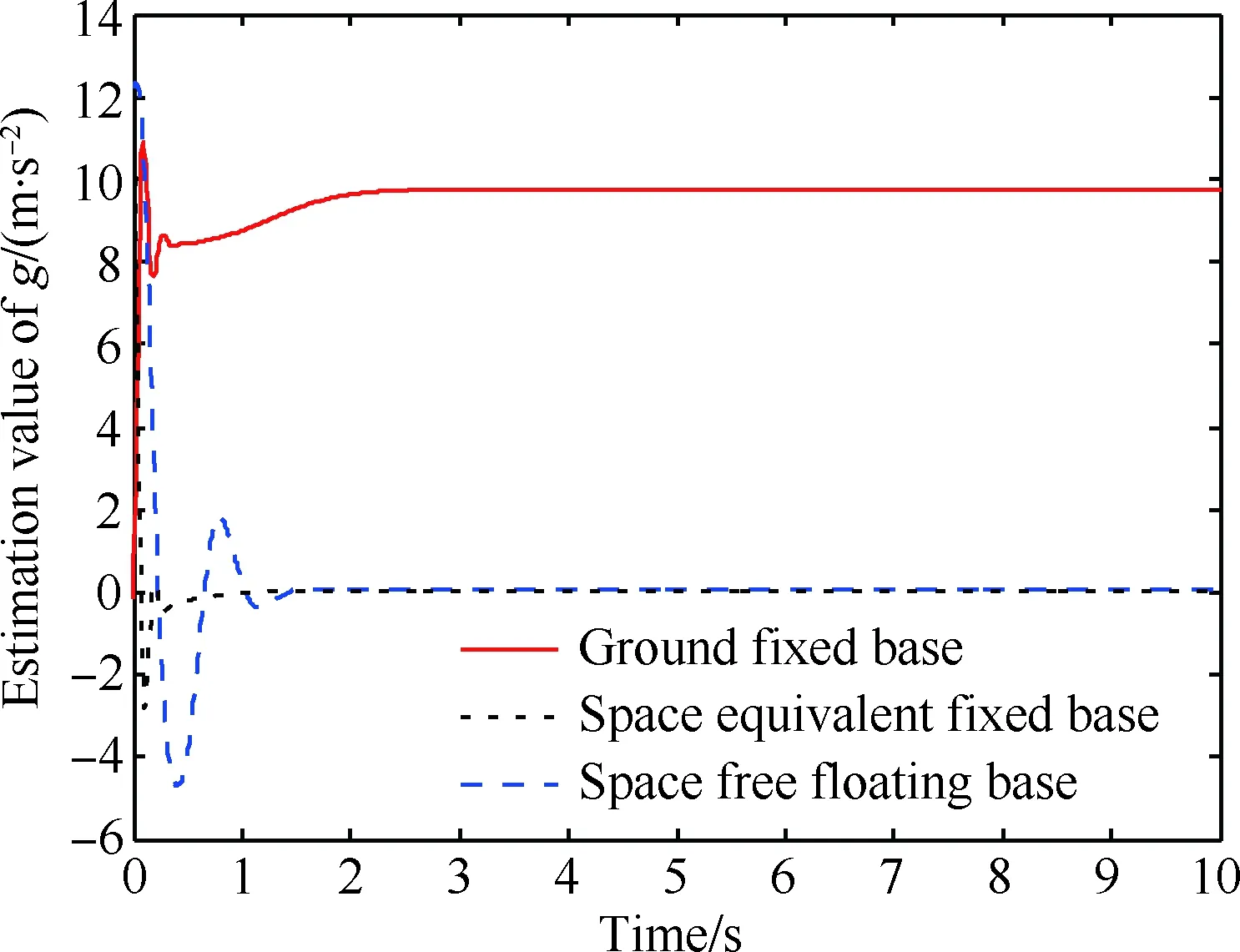
图15 重力加速度g的估计值(mf=200 kg,mb=1 000 kg)Fig.15 Estimation value of gravity acceleration g (mf=200 kg,mb=1 000 kg)

5 结 论

1) 通过对在轨加注过程中，目标航天器、服务航天器和推进剂模块质量特性改变时的空间操作臂系统非线性动力学特性进行仿真分析，验证了变质量特性下常规策略控制的操作臂系统可能发生混沌运动。

2) 参照系统能量变化和自身物理结构设计了自适应镇定控制方案，仿真结果表明了其可实现对重力加速度的有效估计和对空间操作臂非线性动力学响应的自适应镇定，并对外界干扰和参数变化具有一定的鲁棒性。

3) 由于控制策略对变化的控制对象及力学环境的自适应性，可在非服役环境中调试出更有效的参数，在一定程度上降低地面调试问题对系统运动状态和控制性能的影响，有望在地面研发试验中辅助解决重力环境差异的问题。