基于地面任务-空间姿态映射的敏捷卫星任务规划
赵琳,王硕,郝勇,刘源,柴毅
哈尔滨工程大学 自动化学院,哈尔滨 150001
随着航天科学技术的日益完善,敏捷卫星[1-3]的快速发展成为必然趋势,而任务规划作为运控系统中的关键模块[4-5],影响着整个敏捷卫星系统运行的工作效益。相比于传统的非敏捷卫星,敏捷卫星具有更加灵活的观测姿态、更长的观测时间窗口[6]等特点,这些特点使得敏捷卫星任务规划问题的求解更加困难[7-8]。
针对敏捷卫星任务规划问题,Lemaitre等[9]构建了约束规划模型,比较了约束规划、贪婪、动态规划以及局部搜索4种算法,并给出了4种算法的适用范围。Tangpattanakul等[10]基于多目标敏捷卫星任务规划模型,提出了基于指标的多目标局部搜索算法,该方法既能够使任务收益最大又能同时确保资源共享的公正性。郝会成[4]建立了多目标敏捷卫星任务规划数学模型,并提出基于平均互信息提取触发特征改进蚁群求解算法,该方法能够充分发挥敏捷卫星工作效益。Xu等[11]研究了资源约束下的敏捷卫星任务规划问题,提出了基于优先权的结构算法,该算法能够最大限度地提高任务优先级总和。陈成[12]考虑敏捷卫星的时间依赖特性,提出基于有向图适应度评价的混合差分进化算法,该方法能够显著提升敏捷卫星的成像质量。由此可见,智能优化算法在求解敏捷卫星任务规划问题时具有很多优势。
敏捷卫星任务规划较以往的非敏捷卫星任务规划更为复杂。尤其在观测时间窗口相互重叠的多观测任务情况下,任务的观测顺序不再固定,可形成多个满足条件的观测方案。复杂的观测约束和多变的观测方案均对任务规划模型建立和算法设计提出了更高的要求。在以往的敏捷卫星任务规划研究中,观测任务间姿态最小调整时间是通过姿态改变量和平均角速度计算的,忽略了卫星运动学机理,计算得到的最小时间不满足最优性且大于真正的最小时间,缩小了后续待观测任务的可用时间窗,因此在机动能力受限和成像任务冗余的情况下,算法求解效率低,不能有效避免任务冲突。
针对这一缺陷,引入任务-姿态协同规划的思想,将地面观测任务映射为空间姿态区间,同时考虑任务实施方案中相邻任务间姿态调整所消耗时间的最优性。并在此基础上,针对敏捷卫星单星单轨任务规划问题,建立了基于DTSP (Dynamic Travelling Salesman Problem)[13]的任务-姿态协同规划模型。旨在任务编排和选取时,充分考虑卫星姿态机动能力,以此优化姿态调整所消耗的时间,使得任务实施方案中相邻任务间无多余等待时间,进而增强卫星观测效能、有效规避任务冲突。然后,针对任务-姿态协同规划模型,提出了自适应伪谱遗传算法。最后,通过仿真实验,验证协同规划模型和自适应伪谱遗传算法对于敏捷卫星任务规划问题求解的高效性。
1 卫星任务-姿态协同规划问题描述
1.1 地面目标质点模型
以地球惯性坐标系I(C-XIYIZI)为参考坐标系,自西向东旋转角度ωEt,到达地固坐标系E(C-XEYEZE),ωE为地球自转角速度,其旋转关系如图1所示,其表达式为
(1)


图1 坐标系示意图Fig.1 Schematic diagram of coordinate system
1.2 地面观测目标与空间姿态质点映射模型
根据图2所示,假设地球不发生自转,地球球面上点目标T在I系中的坐标为

图2 卫星相对地面目标矢量图Fig.2 Relative vector of satellite to ground target
RCT=RCS+RST
(2)
式中:RCT为地心-目标矢量;RCS为地心-卫星矢量,且在轨道坐标系O-XOYOZO中沿ZO轴负方向;RST为卫星观测地面目标时相机视轴指向。
假设目标T的经纬高为(λ,φ,h),则根据式(1) 和式(2),则有卫星的观测姿态矩阵为

(3)
e2=f(2-f)
(4)
(5)
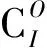
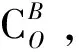
σ=ψ(o,λ,φ,h,t)
(6)
根据图3(a)所示,给出E坐标系下地球表面上圆心为(λ0,φ0,h0)=(118.36°,32.03°,0 m),弧半径为rT=800 rad的一个封闭圆轨迹,其表达式为
rT=Φ(λ-λ0,φ-φ0,h-h0)
(7)
式中:(λ,φ,h)为轨迹上任一点;Φ为计算地球上两点间弧线距离的函数。
取轨道和时间分别为定值o0,t0,则式(7)表达的地面圆轨迹对应的空间姿态区间表达为
ψ(σ)=ψ(o0,Φ-1(r,λ0,φ0,h0),t0)
(8)
o0,t0的取值如表1所示,则式(8)表达的地面圆轨迹对应的空间姿态区间如图3(b)所示。
根据图3(b)所示,地球上封闭圆轨迹对应的姿态空间仍为封闭轨迹,满足式(6)表达的空间姿态与地面观测目标一一映射的关系。


图3 区间映射Fig.3 Interval mapping

半长轴/km偏心率轨道倾角/(°)升交点赤径/(°)近地点幅角/(°)6 978.140.000641.878×10-50年月日时分秒201641441139.687
1.3 任务-姿态协同规划数学模型
根据1.2节的映射关系,将地面观测任务映射为某一空间姿态区间,此时,可以将地面任务编排映射为其对应空间姿态区间编排,使得任务编排时能够充分考虑姿态机动能力约束,以此优化相邻任务间姿态调整所消耗的时间,使其满足最优性条件,进而实现任务观测的无缝衔接,并提高卫星调度过程的紧凑性。
敏捷卫星从一个姿态机动到另一个姿态的过程如图4所示,σk(k=0,f)为任务Tk在tk时刻的姿态。



(9)
此时,上述卫星从状态(σ0,t0)机动至(σf,tf)的终端状态不固定的最小时间问题转化为误差姿态σe→0终端状态固定的最小时间问题,这里定义为规则γ。

图4 姿态机动示意图Fig.4 Schematic diagram of attitude maneuver

图5 姿态指向图Fig.5 Schematic diagram of attitude direction
基于上述变换,选择误差姿态运动方程作为规则γ的系统方程[14-15],表达式为
(10)
(11)
s.t.
(12)
(13)
|uγi|≤umax,|ωe i|≤ωmax,i=x,y,z
(14)
式中:umax为卫星最大控制力矩;ωmax为卫星最大角速度。
且满足性能指标:
Jγ=tf-t0=Δt
(15)
在考虑地面任务-空间姿态映射关系和相邻任务间姿态调整消耗时间最优性后,任务规划问题可以转化为一个复杂的姿态规划问题,这里称作任务-姿态协同规划问题。卫星任务-姿态协同规划问题是指利用卫星资源,针对用户需求,同时制定出合理的满足约束条件的任务实施方案和姿态转移路径。
图6为单颗敏捷卫星对多个待观测点目标实施规划调度的示意图,即卫星在某不发生机动的轨道上飞行时,从零初始姿态开始,采取某种观测顺序,对用户任务需求中任务实施观测,并最终回到零姿态的过程。由于卫星在空中运行时受地光照、地球遮挡以及卫星自身机动能力的限制,其可观测时间窗口有限,卫星在时间窗口内不一定能够对所有任务实现观测,会出现图6(a)中所有任务均被观测和图6(b)中部分任务不能被观测两种现象。


图6 任务观测示意图Fig.6 Schematic diagram of mission’s observation
卫星任务-姿态协同规划问题是多优化目标和多约束的组合优化问题,其本质是DTSP。为简化问题复杂度,不考虑卫星星上能量、存储容量等资源约束以及最长连续工作时间、数据回传等观测约束,建立卫星任务-姿态协同规划问题模型。假设S为卫星资源属性集合,包括执行任务的卫星的轨道参数、机动能力等参数;Rneed为用户任务需求,包括任务的经纬高和持续观测时间;R为任务实施方案序列;t为任务开始执行时间序列;A为任务间姿态转移路径集合;A′为任务持续观测路径集合;tI、tT分别为可观测时间窗口的开始和结束时间;TS和TE为实施方案中为满足DTSP的一般性描述[13]而设置的虚拟任务。卫星任务-姿态协同规划问题P可形式化描述为
P={S,Rneed,tI,tT}
(16)
卫星任务-姿态协同规划问题解Q的数学描述为
Q={R,t,A,A′}
(17)
R=[TST1T2…TnTE]
(18)
t=[tIt1t2…tntE]
(19)
A={AS,1,A1,2,…,An-1,n,An,E}
(20)
(21)

根据式(6),当任务Ti及其结束观测时间ti+di和任务Tj及其开始观测时间tj已知时,其对应的观测姿态σi,σj已知,即任务间姿态机动路径Ai,j的端点姿态和转移时间已知,此时,姿态路径与R、t相关,表示为A=θ(R,t),式(17)变形为
Q={R,t,θ(R,t),A′}
(22)
在采用规则γ优化相邻任务间姿态调整所消耗的时间后,相邻两个任务间的姿态调整时间fti可表示为
fti=minΔti,j(i=S,1,2,…,n;j=1,2,…,n,E)
(23)
式中:minΔti,j为相邻任务间姿态调整所消耗的最小时间。
根据规则γ,开始观测时间t和观测顺序R相关,即t=γ(R),式(22)变形为
Q={R,γ(R),θ(R,γ(R)),A′}
(24)
此时,找到最优解的时间复杂度的数量级为O(n!),是文献[16]求解模型的1/n!。且每一个任务的开始观测时间ti为
(25)
根据式(24),并结合卫星观测任务时可能会出现的两种情况(图6(a)和图6(b)),卫星任务-姿态协同规划问题解的寻优过程转化为,寻得一个最优的观测顺序R,并满足如下目标:
1) 观测目标最多
(26)
2) 时间最小
(27)
3) 能量消耗最小
(28)
s.t.
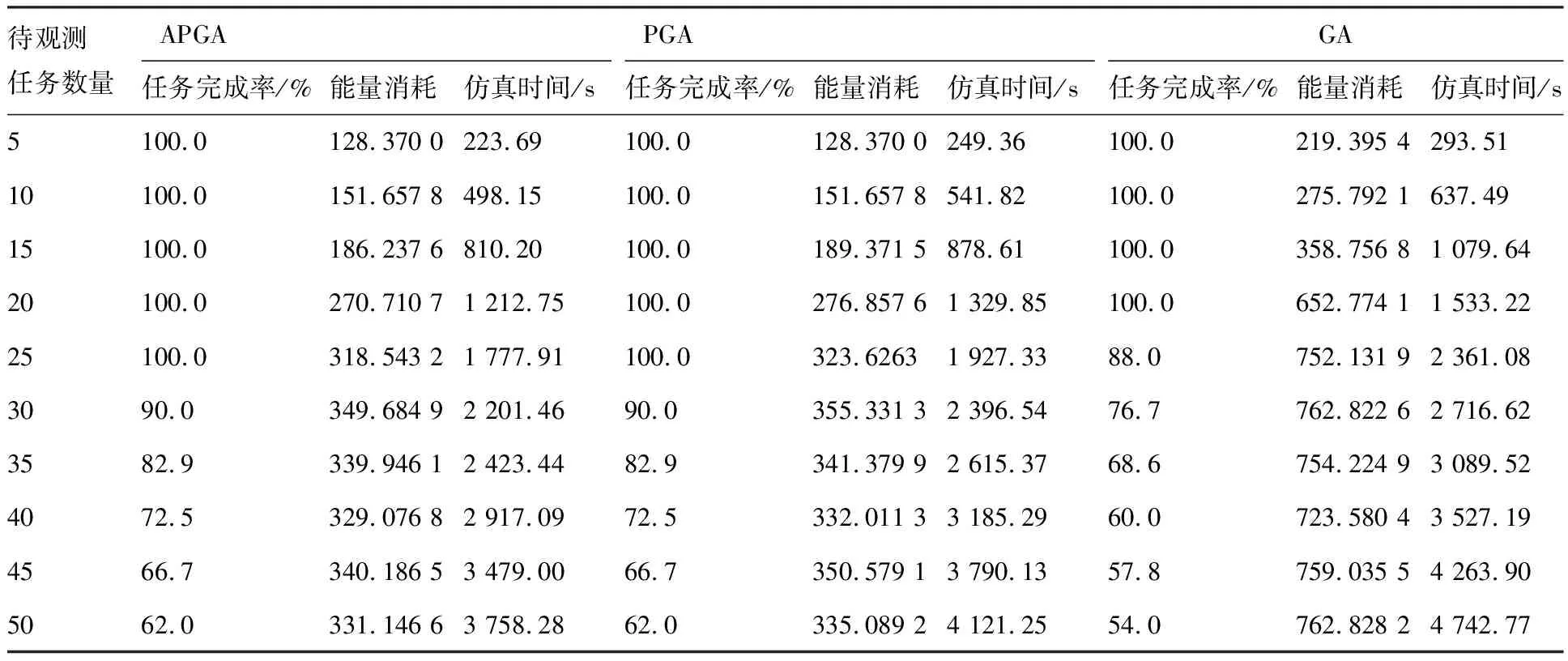
tI (29) |ui|≤umax,|ωi|≤ωmax,i=x,y,z (30) 式中:ai表示第i个任务是否被执行,表示为 (31) fti为任务间转移时间,表示为 (32) fei为任务间转移能耗,表达式为 (33) hei为任务持续观测能耗,表达式为 hei=E(R,di) (34) 对于观测时间窗口相互重叠的多观测任务情况,任务的观测顺序不再固定,不同的观测顺序下所消耗的能量和执行任务所需时间不同,在任务观测顺序选取中应对其进行优化,减小卫星执行任务时的能量消耗和时间,以此提高观测效率,因此除了观测目标最多之外,我们引入时间最小和能量消耗最小这两个优化目标。 在计算E(R,fti)时,需在相邻任务中所有满足约束条件的姿态路径间选择能量消耗最小的一条路径作为Aij,并记为规则δ。此时,规则δ为起止时间、状态均固定的最小能量消耗问题。基于上述定义,选择绝对姿态运动方程作为规则δ的系统方程,表达式为 (35) (36) s.t. (37) (38) |uδi|≤umax,|ωi|≤ωmax,i=x,y,z (39) 且满足性能指标: (40) 此时,规则δ表示为 Aij=δ(σi(ti+di),σj(tj)) (41) 根据1.3节定义,δ、γ规则为最优控制问题[17]。对于最优控制问题,其求解方法有很多,例如智能优化算法[18],极小值原理法[19],伪谱法[20-21]等。而伪谱法既可以通过伪谱协态映射定理证明其计算结果的最优性,又可以有效避免遗传算法的随机性和极小值原理法中推导一阶最优条件与横截条件的复杂性。因此,根据上述优越性,采用伪谱法处理规则δ和规则γ。伪谱法采用插值多项式来逼近一系列离散点上的状态变量和控制变量,对插值多项式求导将微分方程转化为数值约束条件,并通过积分权重来离散估计积分型性能指标,进而将最优控制问题转化为非线性规划问题,然后,采用序列二次规划求得数值最优解。规则δ、γ的求解过程如图7所示。 为最大化利用卫星可见时间窗口,提高可见时间窗口内卫星能够观测的任务数量,采用γ规则优化相邻任务间姿态调整所消耗的时间,使得观测时间和观测顺序相关联,此时,敏捷卫星任务规划问题编码结构可由二维简化为一维,如图8所示。 图7 规则δ、γ求解过程Fig.7 Solution process of rulesδ、γ 图8 染色体结构Fig.8 Chromosome structure 为实现卫星对任务的无重复观测,染色体中每一位基因需要满足: Ti≠Tj(i≠j,i,j=1,2,…,n) (42) 适应度函数的建立需要考虑问题模型中的所有目标函数以及所有限制性约束,而规则δ和规则γ已经有效地处理了相关约束式(29),因此,综合考虑3个目标函数建立适应度函数。 根据1.3节可知,敏捷卫星任务规划问题属于离散型多属性决策问题,其属性集为 F={fA,fT,fE} (43) 遗传算法中种群大小M有限,因此,解的备选方案(编码染色体)也有限,其方案集为 X={x1,x2,…,xN} (44) 对于方案集中的每一个给定的方案,可以列出其属性值为 xi⟺(fA(xi),fT(xi),fE(xi)) (45) 采用未被观测的目标个数n-fA(xi)设计第i个方案的惩罚因子εi,并根据属性集中属性特点,设计敏捷卫星任务规划多属性适应度函数,其表达式为 f(xi)=(w1fT(xi)+w2fE(xi))εi (46) εi=1+n-fA(xi) (47) 式中:当εi≠εj(i≠j)时,适应度的数量级不同,且当εi>εj时,第i个方案的适应度数量级大于第j个方案的适应度数量级;w1、w2为适应性属性权重,由当前种群集合中每个属性的最大值和最小值定义,其表达式为 (48) 1) 选择算子 为提高遗传效率,选择算子采用锦标赛选择,利用锦标赛选择,在第i代种群中随机选择a个染色体,然后将a个染色体中适应值最大的个体选中作为第i+1代群体的父代。该操作重复M次,则得到了第i+1代的父代群体。 2) 交叉算子 根据编码方式的排列性质,交叉算子采用顺序交叉,利用顺序交叉,随机地选择父代染色体中的两个位置,然后如图9所示交换两个位置间的子串。 图9 顺序交叉算子Fig.9 Order crossover operator 3) 变异算子 根据编码方式的排列性质,变异算子采用反转变异。利用反转变异,随机地选择染色体中的两个位置,然后如图10所示反转子串。 图10 反转变异算子Fig.10 Inversion mutation operator 为达到全局最优和运算时间折中的目的,根据适应度值的大小,自适应地改变交叉概率Pc和变异概率Pm。且Pc和Pm的表达式为 (49) (50) 根据任务-姿态协同规划数学模型的特点,本节基于遗传算法框架设计了求解敏捷卫星任务规划问题的自适应伪谱遗传算法,其求解流程示意图如图11所示。 图11 自适应伪谱遗传算法求解流程示意图Fig.11 Schematic diagram of APGA solution 采用APGA求解敏捷卫星任务规划问题,可以实现伪谱法和遗传算法两种算法的优势互补,其具有如下优势:首先,该算法保留了遗传算法中所有个体并行比较的特点,因此,其具备快速随机搜索能力;其次,该方法采用伪谱法处理δ、γ规则,因此与遗传算法相比,其能够有效降低编码和适应度函数的复杂度,提高求解效率;最后,该算法引入任务-姿态同级规划思想,在任务编排和选取同时,优化姿态调整所消耗的时间,得到任务、姿态均可行的有效解,并能够最大化利用卫星可见时间窗口,提高可见时间窗口内卫星能够观测的任务数量,进而并保证输出结果的高效性。 为验证第2节中设计APGA算法的有效性,本节进行数学仿真,并对仿真结果进行分析。 首先,以MATLAB2014b为实验平台,采用CPU为3.40 GHz/i7-6700,操作系统为Win7的计算机做优化计算,设计仿真参数如表2和表3所示。 在半轨周期[2017:3:22:5:38:45-2017:3:22:6:27:45]内选择两个观测时间窗口相互重叠的区间,A [2017:3:22:5:43:38-2017:3:22:5:54:16], B [2017:3:22:6:11:50-2017:3:22:6:20:32],并设计两组观测目标,其参数如表4所示。 表2 系统参数Table 2 System parameters 表3 APGA算法参数Table 3 Parameters of APGA algorithm 表4 地面目标位置Table 4 Positions of ground targets 根据3.1节仿真参数,针对机动能力受限和成像任务冗余两种情况,设计3组不同仿真场景(表5),其中场景1、2验证待观测任务相同而卫星机动能力不同时算法的有效性;场景2、3验证卫星机动能力相同而待观测任务不同时算法的有效性。图12~图14给出了3组场景中,卫星对待观测任务的观测顺序、观测姿态、观测时间以及空间姿态地表投影。表6则分别给出3组场景的观测时间(UTC)、能量消耗,以及仿真计算时间。 表5 场景参数设置Table 5 Setting of scenarios parameters 表6 APGA仿真结果Table 6 Simulation results of APGA 续表 图12 场景1仿真示意图Fig.12 Simulation diagram of Scenario 1 由图12~图14可知,采用APGA可以得到高质量的平滑姿态轨迹,这是由于APGA采用伪谱法处理δ规则。同时2D姿态地表投影表明将地面观测任务映射为某一空间姿态区间,以及将地面任务编排映射为其对应空间姿态区间编排是合理的。 图13 场景2仿真示意图Fig.13 Simulation diagram of Scenario 2 图14 场景3仿真示意图Fig.14 Simulation diagram of Scenario 3 对比图12~图13和表6中场景1、2的仿真结果可知,当卫星机动能力较小时,在重叠观测时间窗内,卫星不能对成像序列中所有任务进行观测,任务出现冗余;而当机动能力较大时,卫星能够实现对更多的任务进行观测。此结果表明,在机动能力限制较大卫星任务规划问题中,APGA仍能得到其有效解。 对比图13~图14和表6中场景2、3的仿真结果可知,当卫星成像序列中任务较少时,在重叠观测时间窗内,卫星能够实现对成像序列中所有任务进行观测;而当卫星成像序列中任务较多时,卫星不能对成像序列中所有任务进行观测,任务出现冗余。此结果表明,对于非冗余和冗余卫星任务规划问题,APGA均有效。 为验证所设计算法APGA的优越性,以场景1为例,将遗传算法(Genetic Algorithm, GA)、伪谱遗传算法(Pseudo-spectral Genetic Algorithm, PGA)与APGA进行对比。 对比图12、图15、图16和表6、表7的仿真结果可知,在相同仿真条件下,APGA和PGA在任务观测数量、能量消耗、姿态轨迹、空间姿态地表投影和运算时间上均优于GA,这是由于①上述设计的任务-姿态协同规划模型中考虑了姿态间转移时间的最优性(规则γ),使得卫星从一个观测姿态机动到另一个观测姿态无时间浪费,实现紧凑观测,并为后续任务的观测提供更大的可用时间窗;② APGA和PGA采用伪谱法替代遗传编码来处理规则δ,则不需要对相邻两个姿态间的姿态路径进行编码,降低了遗传算法中编码的维数,此时,不仅有效避免了遗传编码导致的曲线抖动现象,并且能够提高姿态轨迹和空间姿态地表投影的平滑性,以此降低能量消耗,提高算法求解效率。 表7 GA和PGA仿真结果Table 7 Simulation results of GA and PGA 图15 遗传算法仿真示意图Fig.15 Simulation diagram of GA 图16 伪谱遗传算法仿真示意图Fig.16 Simulation diagram of PGA 待观测任务数量APGAPGAGA任务完成率/%能量消耗仿真时间/s任务完成率/%能量消耗仿真时间/s任务完成率/%能量消耗仿真时间/s5100.0128.370 0223.69100.0128.370 0249.36100.0219.395 4293.5110100.0151.657 8498.15100.0151.657 8541.82100.0275.792 1637.4915100.0186.237 6810.20100.0189.371 5878.61100.0358.756 81 079.6420100.0270.710 71 212.75100.0276.857 61 329.85100.0652.774 11 533.2225100.0318.543 21 777.91100.0323.62631 927.3388.0752.131 92 361.083090.0349.684 92 201.4690.0355.331 32 396.5476.7762.822 62 716.623582.9339.946 12 423.4482.9341.379 92 615.3768.6754.224 93 089.524072.5329.076 82 917.0972.5332.011 33 185.2960.0723.580 43 527.194566.7340.186 53 479.0066.7350.579 13 790.1357.8759.035 54 263.905062.0331.146 63 758.2862.0335.089 24 121.2554.0762.828 24 742.77 图17 3种算法收敛性比较Fig.17 Comparison of convergence among three algorithms 对比3组算法的仿真收敛性曲线(图17),GA全局搜索能力差,PGA优之,APGA搜索能力最强。这是由于APGA和PGA采用伪谱法替代遗传编码来处理规则δ,降低了遗传算法中编码的维数,进而降低问题求解的时间复杂度,从而提高算法的收敛精度和收敛速度;此外,APGA自适应地改变Pc和Pm的值,维持种群多样性,使算法在陷入局部收敛时能够快速跳出,进而提高算法收敛精度和解的质量。 此外,为进一步验证所设计模型和算法的优越性,设计10组不同任务数量的仿真场景,每组场景运行10次,运算结果取均值,并与PGA和GA运算结果相比较,结果如表8所示。 分析仿真结果可知,在相同仿真条件下,APGA解的质量更好,且求解速度相对较快,但是随着任务规模的增大,其运算时间也会大幅度增加。从表8中可以看出,在任务规模较小时,3种算法任务完成率相同,但当任务规模较大时(即任务冗余),APGA和PGA的任务完成率高于GA。对比APGA和PGA仿真结果,在不同仿真规模下,二者可以得到相同的任务完成率,但APGA的仿真结果在能量消耗和仿真时间上均优于PGA,进一步验证了自适应遗传参数的引入对于提高算法收敛精度和速度的有效性。 1) 基于任务-姿态协同规划的思想,将地面观测任务映射为空间姿态区间,并充分考虑姿态机动能力约束,以此最优化相邻任务间姿态调整时间,建立任务-姿态协同规划数学模型。 2) 根据任务-姿态协同规划的数学模型以及模型中设计的规则δ、γ的特点,设计了自适应伪谱遗传算法。 3) 仿真实验中,针对卫星机动能力受限和成像任务冗余两种情况,对算法的有效性进行了分析并与PGA和GA运算结果相比较,验证算法的优越性。仿真验证表明,将地面任务编排映射为其对应空间姿态区间编排是合理的,且同时考虑相邻任务间姿态调整时间最优性是可行的,即任务-姿态协同规划数学模型适用于敏捷卫星任务规划问题;且APGA既能够有效地解决GA在机动能力受限和成像任务冗余两种情况下求解效率低的缺陷,又能够通过引入自适应遗传参数有效提高PGA算法的收敛精度、降低能量消耗,输出满足最优性需求的任务、姿态均可行的有效解。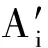


2 自适应伪谱遗传算法(APGA)
2.1 伪谱法处理δ规则和γ规则
2.2 染色体编码


2.3 适应度函数建立
2.4 遗传算子


2.5 自适应控制参数

2.6 自适应伪谱遗传算法计算流程

3 仿真验证
3.1 参数设置



3.2 APGA有效性验证








3.3 算法对比和结果分析







4 结 论

